在数学学习中培养创新能力

吴健军

现时正处于新世纪初期，二十一世纪需要有创新能力的人，这是新世纪人才规格的特点。培养具有创新能力的人，是时代赋予全社会的职责。有创造才有发展，创新是社会发展的动力。社会对人才的需求要求我们培养出具有创新意识、创新勇气和创新能力的一代新人。因此，我们这些数学基础教育工作者在平时的教学中应努力培养学生的创新能力。那么，什么是创新能力？如何在日常课堂教学中实施创新教育，培养具有创新能力的人才？本人根据近几年的教学就这些问题阐述一二：

1对数学创新能力的理解

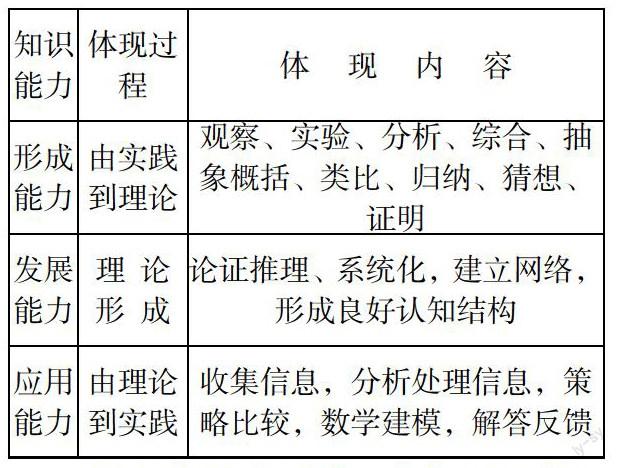
数学创新能力是数学的基础、一般的能力，包括对数学问题的质疑能力、建立数学模型的能力（即把实际问题转化为数学问题的能力）、对数学问题猜测（想）的能力等。数学创新能力的能力体现主要在三个方面，即知识形成的能力、知识发展的能力、知识应用的能力，它们的体现过程和主要内容可列表如下：

显然，创新能力在数学知识的形成、发展、应用三个过程中都有体现，并具有各自的内容和特征，在数学教学活动中，教师应特别重视对学生创新能力的培养，使每一个学生都养成独立分析问题、探索问题、解决问题和延伸问题的习惯。让所有的学生都有能力提出新见解、发现新思路、解决新问题。

2新理念下的课堂教学方式

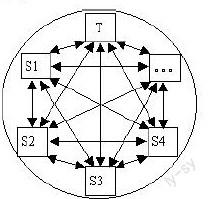
在关注学生的进步或发展、关注教学效益的有效教学理念下，以师生合作探讨式的课堂教学方式开展教学活动（如右图）。

3课堂教学中创新能力培养的具体方法

在数学学习中如何培养学生的创新能力是摆在每一个教师面前的一个课题。笔者认为课堂教学里可通过以下几个方面来培养。

3.1营造创新氛围

周忠昌在《创造心理学》一书中指出：“有利于创造的风气，不仅会促进求知欲滋长旺盛，激发探索异常解决办法的强烈兴趣，而且还会刺激新思路的开拓。”因此，在课堂教学中建立和谐的师生关系，师生、同学间相互尊重、相互激励，使学生成为教学主体；帮助学生培养乐于提出新问题，养成质疑的习惯，对学生的创新成果给予适当奖励，即使是尚未成熟的创造性设想，也要积极支持，努力保护学生创新的积极性；促进形成激励创新的环境。

例如 ：在《三角形内角和定理》的知识学习中，我选择的尝试点是：在小学我们曾用折叠一个三角形纸片把三角形的三个角拼在一起，得到“三角形三个内角的和等于是180°”这个结论（实物演示）。但通过实验我们得到的只是感性认识，而几何是一门说理学科，同学们知道其理论根据是什么吗？这样的问题提出，即不以感知直观为出发点，更不以告诉现成的知识结论或解决途径为出发点，而是创设问题情境，激发学生求知欲，让他们在迫切要求下进行学习。

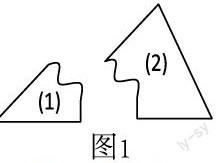
再如：一块三角形的玻璃被打碎成二片（如图1），要配成一块同样大小的三角形玻璃，是否将二块都带去？若只带一块，那么应带哪一块？为什么？这是生活中一个活生生的事例，问题一经提出，同学们都兴奋不已，有的拿尺比划着，有的用圆规度量着，学生的思维瞬间被激活，有的学生说两块都拿去，有的说将第（1）块拿去，有的说将第（2）块拿去就可以了，最后有一个同学很自信地说只要将第（1）块拿去就行了，但原因他也说不清楚，只是直觉而已。这时整个课堂气氛进入“高潮”，学生的思维处于萌動状态，他们想要知道个中原由，因此师生很自然就导入“全等三角形”的课题。

这样，在课堂教学中通过设计、创设问题的情境去诱发学生某种创新的动机，使其表现出创新的意向和愿望，这是学生在数学学习中创造性活动的出发点和内在动力。

3.2培养观察能力

观察是通往创造世界之门的第一步。而数学观察能力是顺利完成数学活动所必备的且直接影响其学习效益的一种个性心理特征。它是获取知识、提高能力的门户，是智力发展的基础。在课堂教学活动中，本人认为可以从以下几个方面入手：

3.2.1引导学生选择观察点

对数学式子结构的观察，选择恰当的观察点，由点及面，由此及彼，由表及里，由具体到抽象，往往会起到事半功倍的作用。例如解方程：.引导学生仔细地观察，发现将方程右边的5移至左边，则左边根号内外的式子相同，进而将原方程变形为：；接着让学生明白变形方程的意义是： x-5的算术平方根是它的相反数。进而问学生：什么数的算术平方根是它的相反数？学生想到“只有0的算术平方根是它的相反数”后，自然有x-5=0，从而得原方程的解x=5。我们可以直接通过观察就能得到解题结果。

3.2.2在联系中进行观察，观察规律，寻求思路

通过观察各元素之间的关系，发现它们的内在联系，从事物的构成规律上来把握问题的实质，寻找解题思路，使问题得到解决。例如：求1！+2！+3！+...+2004！的个位数字。观察n！（n=1，2，3，...）中个位数字的规律：1！=1 个位数字为1；2！=2 个位数字为2；3！=6 个位数字为6；4！=24 个位数字为4；5！=120 个位数字为0；6！=720 个位数字为0；...。可见n≥5时，n！的个位数字都是0，因此1！+2！+3！+...+2001！的个位数字应是3。

只要在课堂教学中把观察能力的训练落实到每一环节中，引导学生恰当运用观察，定能全面地培养学生的创新能力。

3.3引导放散思维

在课堂教学中引导学生正确运用求异思维，鼓励学生遇到问题深入思考，打破常规，力求从其他角度解决问题；启迪学生逆向思维，让学生从反面去寻找解决问题的办法，思维的方向变了，就易于产生新的解决问题的方法和途径；鼓励学生多采用求同思维，激发学生用多种方法，寻求更多的解决问题的空间，多种途径解决同一个问题是数学课堂教学培养发散思维，发展创造性思维的一条有效途径。

例如有如下问题：已知，如图（1）AC=AD，∠CAB=∠DAB，求证：ΔACB≌ΔADB。在这个问题解决后，我设计了以下系列的问题组：变试1、如果略去∠CAB=∠DAB，即为：AC=AD，你能补充上什么条件？ （∠CAB=∠DAB，或AB平分∠CAB）；变试2：如图（2）要证明ΔADF≌ΔCBE你能补充上什么结论？（AD=BC，∠A=∠C，AF=EC，或AD=BC，∠A=∠C，AE=CF或AD∥BC，AD=BC等等）；变试3、如图（3）要证明ΔABC≌ΔCDA，你能给出怎样条件。变试4、如图（4）要证明CE=BD，你又能给出怎样的条件？

实践证明，当第一个问题得到解决后，同学们在教师引导下对问题的思维层层递进 进行，横向的拓宽与纵向的深入，探索新的解题思路与方法，这样无论从内容的发散还是解题思维的深入都能起到固本拓新之用，达到了创新能力的培养目的。

3.4增强自主意识

自主意识是发展创新能力的基础和前提。在平时的数学教学活动中，培养学生在探索过程中知难而进、锐意进取、锲而不舍的精神，克服自卑心理和依赖思想，养成喜爱钻研，不满足于已有知识及解答的心理素质以及思考问题时力求深入、全面、慎密的习惯能力。鼓励学生不迷信书本，不迷信教师，敢于独立思考，树立追求真理和发展真理的勇气和信心，这样就能激励学生打开思维闸门，去合理怀疑，去积极探索，去追求真知。

3.5鼓励大胆想象

探索和创新的起点是置疑。也就是说，发现、发明和创新一般往往是从实践或理论研究中发现了问题，提出了问题，从而激发人们去探究问题。

例如在《等腰梯形的判定》学习中，提问：梯形的定义后，教师在黑板上以一条线段的两个端点为顶点在线段的同侧作出两个相等的角，角的另外两边相交于点A，如图：问：你能得到什么结论？（AB=AC）师：如果在AB上取D，过点。过点D作DE∥BC你还能得到什么结论？（AD=AE；BD=EC），师：如果擦去阴影部分，四边形DECB是什么图形？（等腰梯形）为什么？（定义）师：证明四边形DECB是等腰梯就是证明DB=EC那么，证明两条线段相等我们学过哪些证明方法呢？（生回答）师：哪么又做出怎样的辅助线？也就是把新问题归结到怎样的旧知识中才能加以解决呢？

在这类问题的解决中，教师珍惜、爱护、鼓励学生的好奇心及想象力，当有的学生发现和提出含有某种创新因素的”新奇”问题的时候，教师不忙于解答，而及时抓住这种难得的机会或苗头，因势利导，把它作为一个有意义的问题，让全体同学共同思考，这不仅极大鼓舞提出问题的个别学生，还在学生中形成一种勇于大胆想象，喜爱独立思考的良好环境，并在这种良好环境中逐步锻炼了学生善于发现问题、提出问题的本领，从而达到最终的培养目的。

3.6培养实践能力

李时珍尝百草而著出世界药典《本草纲目》。居里夫人经过四年的实验，才提炼了镭。前人的伟绩说明，无数次失败与成功的实践可以获得创新能力。现在，我们在中小学科技课中看到，学生对参加科技创作活动的兴趣远远超过背公式。有些学生在野外活动或校内文体活动中，顯示了很强的组织创造力。在我们的数学课程学习中，一定要加强第二课堂的活动，鼓励学生进行小制作、小实验、小发明、小创造活动，多给学生动手机会，推动学生创新能力的提高。

3.7健全人格特征

希腊哲学家赫拉克利特曾说：人的性格，就是他的命运，人要经受失败与挫折的考验，要防止成功后的骄傲。伟大的文学家高尔基是个性格十分坚强的人，从一个杂工成为一名伟大的文学家。所以成功也往往依赖于人的性格。积极、坚强的性格是产生人的创新能力的保证。所在在日常的课堂教学中，我们要注意完善学生的人格，以保证学生的创新能力的成功培养。

总之，我们应当在平时的数学课堂教学中努力培养学生的创新能力。有创造才有发展，创新是社会发展的动力。社会对人才的需求要求我们培养出具有创新意识、创新勇气和创新能力的一代新人。让我们都去努力吧！

参考文献：

[1]胡久忠编.福建师大数学与计算机科学学院中数教研室.数学教育学.

[2]郭立昌.北京教育科学研究院.构建中学数学创新教育教学模式体系.

[3]朱少华.江都市丁沟中学.谈培养学生创新能力的途径.