基于时间序列的太子河流域降水量的预测

韩明友

（辽宁省水文局，辽宁 沈阳110003）

1 概 述

时间序列预测法是在分析时间序列变量的基础上，运用一定的数学方法建立预测模型，时间趋势向外延伸，从而获得序列的发展变化趋势，确定变量的预测值。即通过时间序列的历史数据揭示现象随时间变化的规律，将这种规律延伸到未来，从而对该现象的未来做出预测，也叫历史延伸法或外推法，具有以下特点：

首先，序列的数据或数据点的位置依赖于时间，即数据的取值依赖于时间的变化，但不一定是时间的严格函数。其次，每一时刻上的取值或数据点的位置具有一定的随机性，不可能完全准确地用历史值预测。再次，前后时刻(不一定是相邻时刻)的数值或数据点的位置有一定的相关性，这种相关性就是系统的动态规律性。

2 平稳时间序列分析原理及步骤

平稳时间序列预测是建立在对历史数据分析之上，历史数据越多越准确，预测也越可靠。平稳时间序列的主要特点是过程的统计性质不随时间的平移而变化。本文所使用的预测方法是时间序列分析中的平稳时间序列预测方法。

设yt（t=1，2，……）是一个随机时间序列，即是对每一个固定的t，yt是一个随机变量。如果yt满足下述条件：均值和方差：Eyt=m，t取一切整数，m为常数：

协量差函数和相关函数：

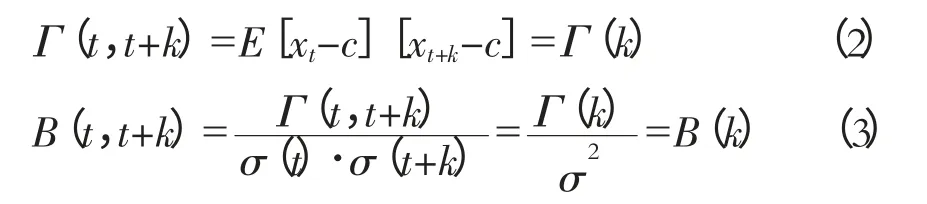
则称此时间序列{yt}为平稳时间序列。

使用平稳时间序列进行预测有很多种方法，这里采用平稳时间序列的线性外推法进行建模预测，建模预测的步骤如下：

1）由{yt}的一组观测值y1，y2，…，yN，先按状态分类，然后计算样本平均数和各个数据的距平值。即：

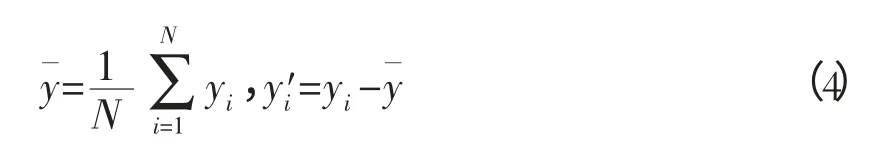
2）由相关函数的性质及计算误差精度，确定预报方程阶数m，一般取小于资料阶数的1/4，也可以取几种不同阶数分别进行预报值比较，选择与历史资料吻合最好的作为应取阶数。

3）在最小二乘法原则的基础上，确定线性最优预报方程

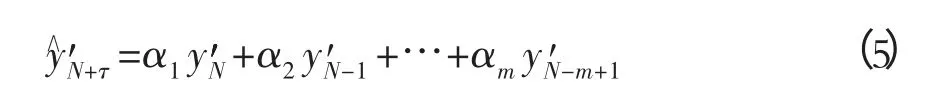
其中τ取正整数（外推步长）。

4）计算B（0），B（1），…，B（m），解线性方程组

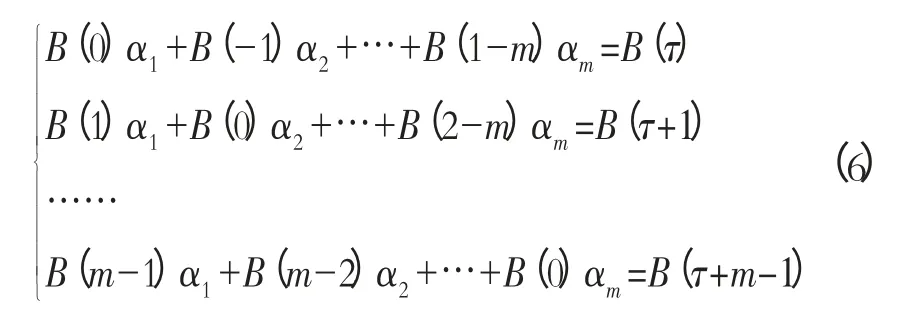
确定系数α1，α2，…，αm。

6）利用下式得到最终的预测值：

3 应 用

根据苇子峪站的1982—2005年每年5月份降水量统计资料，预测2006年5月份的降水量以此预测发生旱灾或是涝灾。历史数据如表1所示。

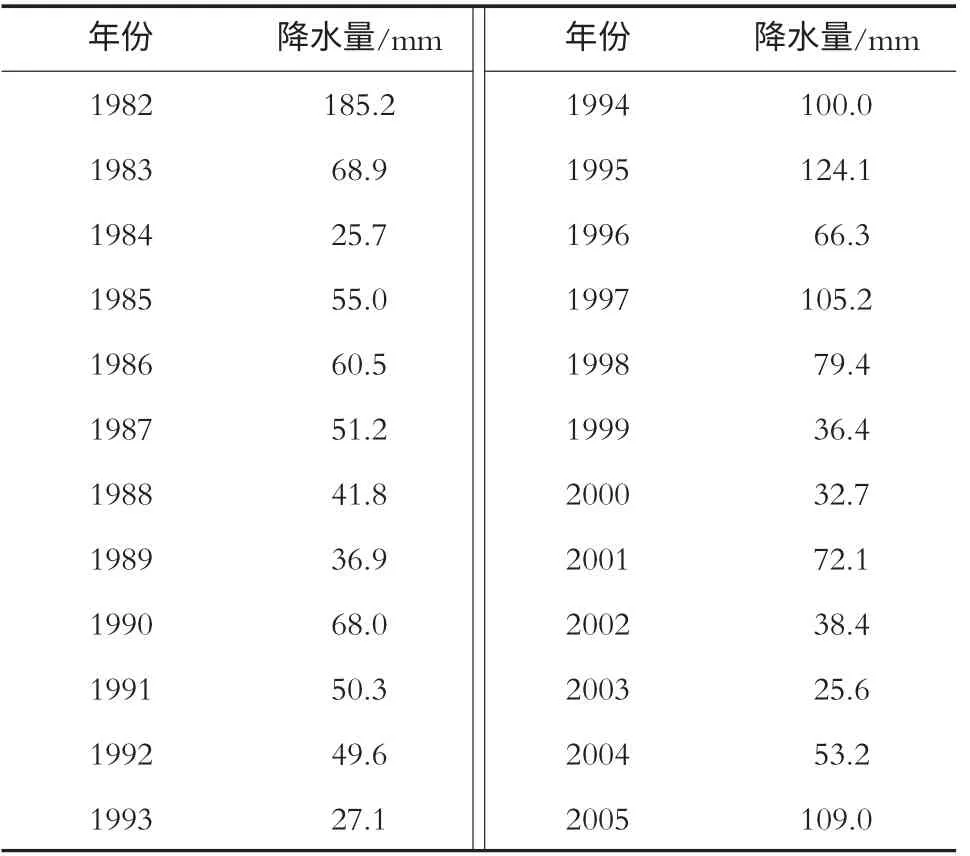
表1 苇子峪站1982—2005年各年5月份降雨量表 mm

计算步骤如下：

1）确定旱涝指标根据多年年平均降水量选定干旱指标，对这些数据进行处理，根据指标Z＜-0.842作为旱年（即降水量小于35 mm），Z＞0.842作为涝年（即降水量大于65 mm）。计算苇子峪站近24年的平均降雨量：

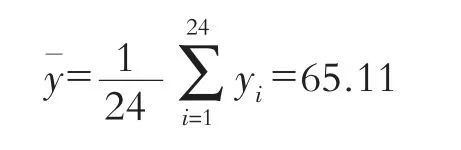
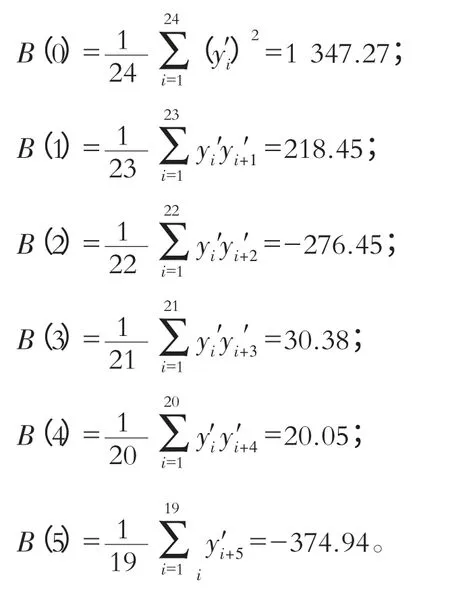
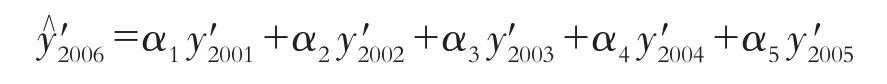
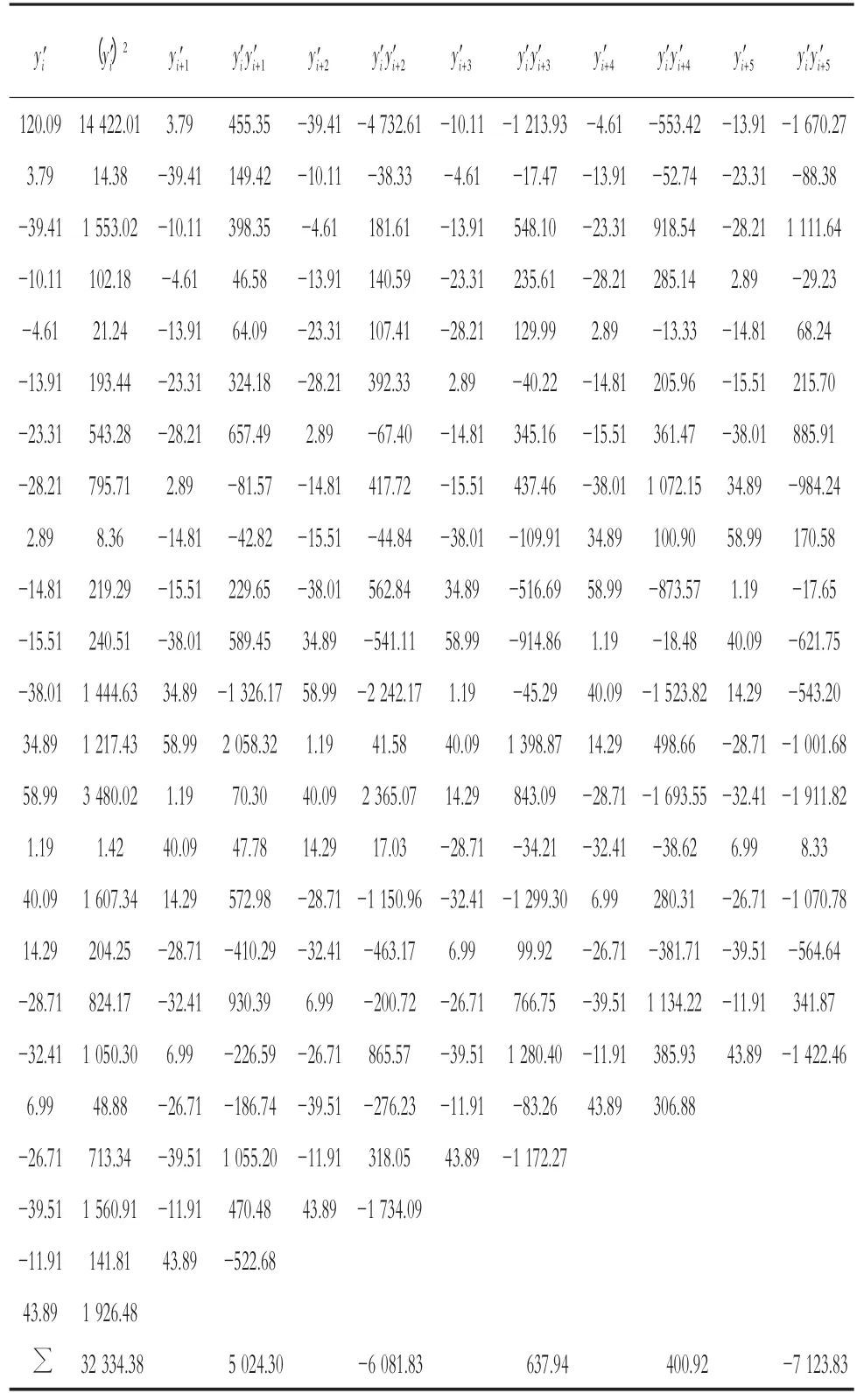
表2 B（k）计算表

对这些数据进行处理，得线性方程组

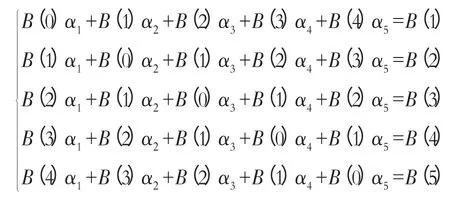
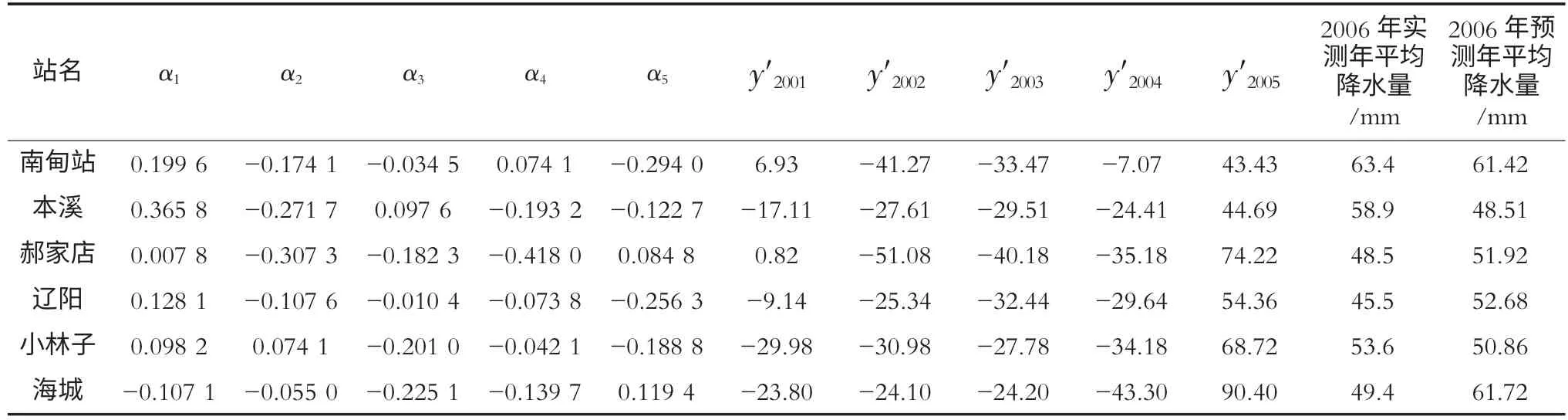
表3 平稳时间序列分析法预测各测站5月份降雨量表

将B（0），B（1），…，B（5）的数值代入上述方程组并解得：

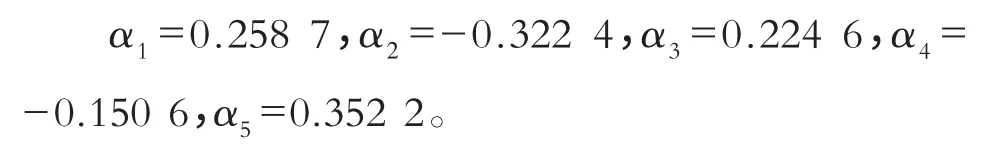
2）预测2006年5月份该地降雨量及状态

将上述α1，α2，…，α5的数值代入预报方程式（7）得自回归预报模型：

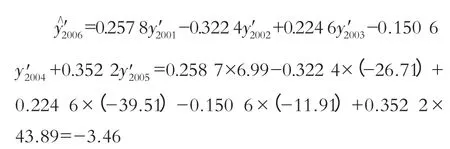
故2006年5月份该地的降雨量预测值为：

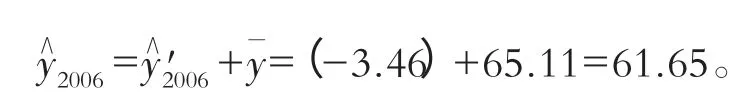
以上预测降水量大于35 mm，属于正常年气候。实际上苇子峪站2006年5月份是正常年份，预测结果与实际相吻合。同理根据此预报模型方法可预测太子河流域其它测站（2006年）5月份的降雨量均为正常年气候，见表3。

4 结 语

用时间序列分析建立太子河流域降水量预测模型，降水量的实际值与预测值相比较，其相对误差绝对值的均值为6.34%，相对误差绝对值均小于10%，都得到了与实际相符合的结果，能够反映出真实情况，预报效果较好，重点在于及时掌握太子河流域降水情况的发生、发展过程、变化趋势以及对农业生产的影响，以便通过及时有效的实时调度，最大限度地减轻旱涝灾害的损失。