幂律型煤油凝胶在不同几何构型管道的流动特性数值研究
曹琪,封锋,武晓松,陈超
(1.南京理工大学机械工程学院,江苏南京210094;2.安徽神剑科技股份有限公司,安徽合肥230001)
幂律型煤油凝胶在不同几何构型管道的流动特性数值研究
曹琪1,封锋1,武晓松1,陈超2
(1.南京理工大学机械工程学院,江苏南京210094;2.安徽神剑科技股份有限公司,安徽合肥230001)
为了优化煤油凝胶供给管道和锥形喷注器设计,构建出幂律流体的二维/三维稳态层流的求解方法,采用基于FLUENT平台的SIMPLE算法进行求解,开展煤油凝胶的流动特性数值研究。推导出了推进剂在直圆管中各参数的解析解以及层流的动能修正系数。研究结果表明:直圆管的柱塞流区域在管径不变时是固定的;为降低喷注器出口截面的平均表观粘度,需减小出口段长度;喷注器的收缩角选择在40°左右是较为合理的;弯管内存在双涡旋形式的二次流,且剪切速率和表观粘度的非对称性比速度的非对称性显著。
兵器科学与技术;煤油凝胶;压力损失;动能修正系数;平均表观粘度;二次流;非对称性;幂律流体
0 引言
凝胶推进剂是用少量凝胶剂将液体组元凝胶化,形成具有一定结构和特定性能并能长期保持稳定的凝胶体系[1]。Kraynik等[2]编写了有限元程序FIDAP并提出使用边界层理论模拟收敛管道的幂律流体流动。Rahimi等[3-4]和Natan等[5]计算出凝胶推进剂在锥形喷注器中的速度与粘度场,认为平均表观粘度在喷注器出口明显减小。左博等[6]、张蒙正等[7]对凝胶推进剂模拟液在直管、弯管和收缩/扩张管的流动进行实验和数值研究,认为几何结构参数对流动损失有显著影响。强洪夫等[8]讨论了收缩角、体积流率和凝胶剂含量对锥形喷注器内流动特性的影响,研究表明收缩角是引起粘度变化的重要因素。Changjin等[9]对凝胶推进剂管流进行了非稳态三维N-S数值模拟,研究表明触变性流体处于牛顿流体和稀化流体的中间流动特性。
本文构建了幂律流体的二维/三维不可压缩稳态层流的求解方法,采用基于Fluent平台的SIMPLE算法进行求解,开展煤油凝胶在直圆管、锥形喷注器管道和弯管的流动特性数值研究,得到其流阻和流变特性涉及的相关结论和规律。对于进一步优化供给管路及喷注器设计具有一定的理论指导意义。
1 数学模型建立与求解
1.1控制方程组
煤油凝胶的流动满足二维/三维稳态不可压缩等温下的N-S方程组。
1)连续方程

2)动量方程

式中:

对于三维流动含有u、v、w、p、η 5个未知数,对于二维流动含有u、v、p、η 4个未知数,方程组不封闭,因此需要补充本构方程。
3)本构方程。本文采用Power-Law[10]本构模型。


对于二维流动来说,以上关于z和w的项都为0.本构方程参数如表1所示。

表1 幂律本构方程参数Tab.1 Parameters of power-law constitutive equation
1.2网格绘制
根据凝胶火箭发动机供给和雾化系统设计需求,选择直圆管、锥形喷注器管道和弯管结构模型。对所需计算的网格进行划分,直管和锥形喷注器管道采用二维轴对称结构网格,弯管采用三维六面体网格,由于速度梯度在壁面处较大,且粘度梯度在轴线处较大,因此在壁面和对称轴处进行网格加密处理[11]。如图1所示。
2 直圆管的流动特性研究
2.1直圆管的流阻特性
沿程阻力损失是煤油凝胶管道输送过程中的重要参数,在供给系统能耗中占有很大比重。这里主要分析在直圆管中的沿程阻力损失随影响因素的变化规律。由文献[12]可知,幂律流体直圆管两端的压降Δp为

式中:R为圆管半径。可求得沿程阻力损失为hl= Δp/ρg.

图1 3种管道的网格划分Fig.1 Mesh generation of three kinds of pipelines
数值计算工况:1)管径D=10 mm,流量Q分别为7.85 mL/s、39.27 mL/s、78.54 mL/s,管长L在50~550 mm之间。2)管长L=200 mm,管径D在3~20 mm之间,其他和工况1相同。得到直圆管沿程阻力的解析解和数值解,如图2、图3所示。
由图2和图3可知,解析解同数值解误差很小。当流量和管径一定时,沿程阻力损失同管长呈正比,且随流变指数的增大而增大;当流量和管长一定时,沿程阻力损失同R1+3n呈反比。
2.2直圆管的流变特性
煤油凝胶在直圆管横截面的轴向速度为
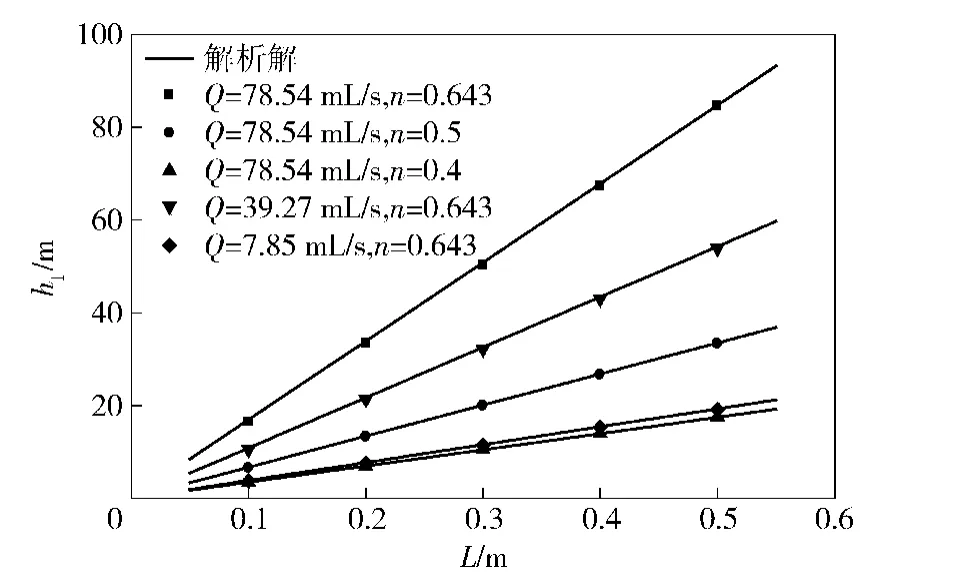
图2 沿程阻力损失hl随管长的变化(D=10 mm)Fig.2 Resistance loss vs.pipe length(D=10 mm)
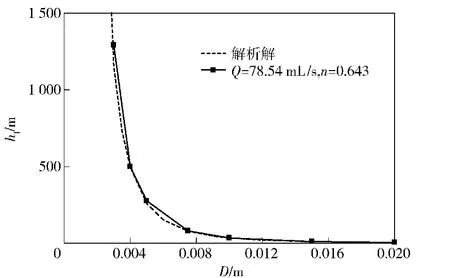
图3 沿程阻力损失hl随管径的变化(L=200 mm)Fig.3 Resistance loss vs.pipe diameter(L=200 mm)

平均速度分布为

由(8)式、(9)式可得

对(8)式求导取负并代入(7)式可得

将(11)式代入幂律本构方程可得

由图4可知,解析解和数值解的误差很小。对于同一种煤油凝胶来说,管径相同时,不同流量的轴向速度无量纲化后的曲线重合,表明无量纲速度不随流量发生变化。若根据无量纲速度曲线判断,则管内“柱塞”流区域分布是固定的。流变指数增大,“柱塞”区减小。在“柱塞”流区域内,速度几乎不变,剪切速率趋于0,表观粘度的梯度很大,且远高于壁面处的表观粘度值。
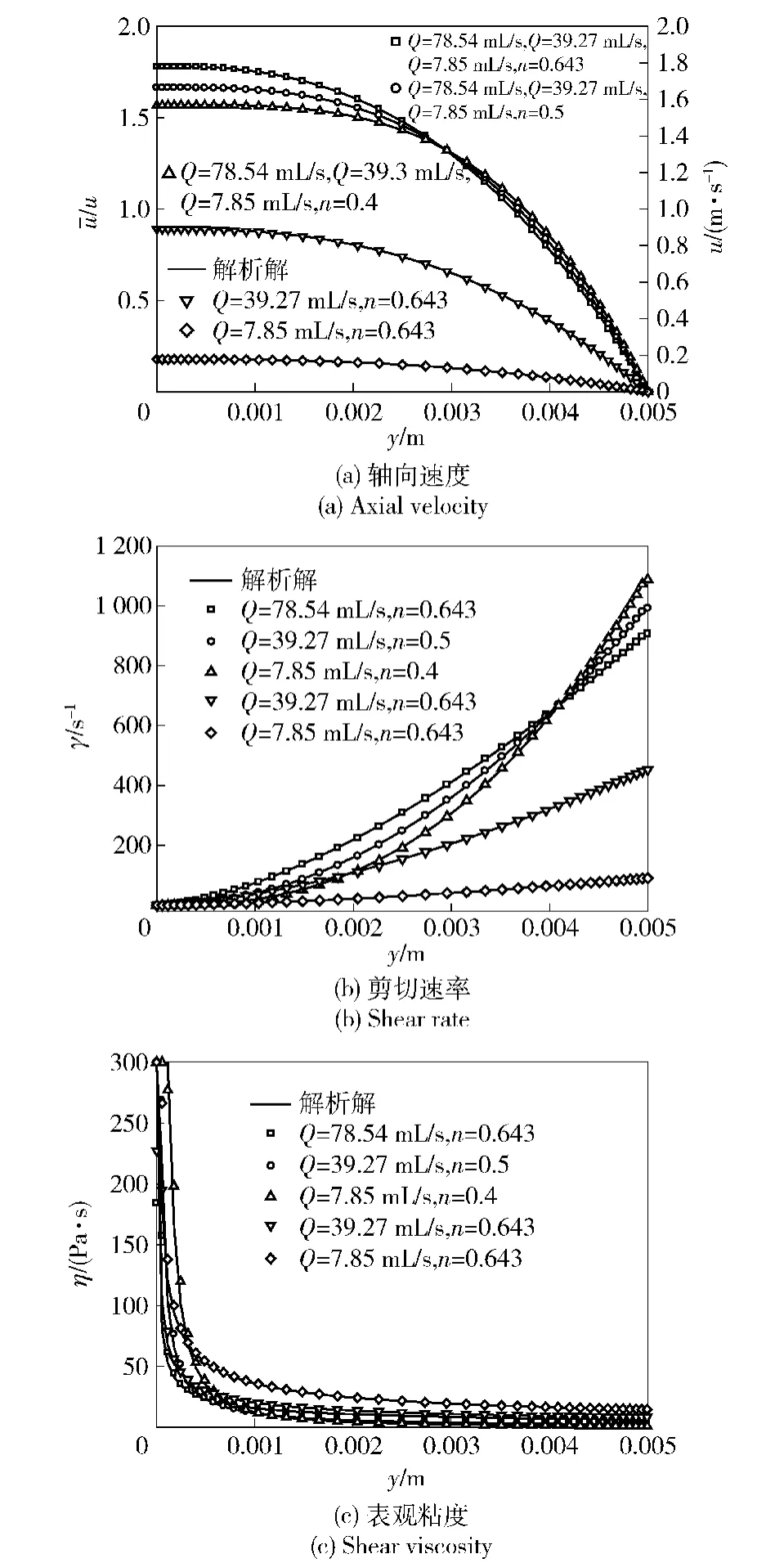
图4 直圆管横截面轴向速度、剪切速率和表观粘度分布Fig.4 Axial velocity,shear rate and shear viscosity of cross section in straight pipe
3 锥形管道的流动特性研究
3.1流阻特性
国内外文献表明[13-15],凝胶推进剂雾化所采用的是锥形喷注器。锥形喷注器的几何结构如图5所示。计算工况为:喷注器出口直径d2=1 mm,收缩比d1/d2分别为2、2.5和3,收缩角θ为10°~60°,流量Q分别为20 mL/s、30 mL/s和40 mL/s.

图5 喷注器几何结构Fig.5 Geometric structure of injector
取距收缩段两端各0.5 mm处的1-1和2-2截面,两截面处u≠0,v≈0,均属于缓变截面,忽略重力列伯努利方程,得

式中:a1、a2为动能修正系数;pm为压力损失。由文献[16]可知,流体在管内流动的动能修正系数a为

将(8)式和(9)式代入(14)式,求得幂律流体的管内动能修正系数为

对于牛顿流体,n=1,得a=2,同文献[16]中一致,可见牛顿流体是非牛顿流体的一个特例。对于非牛顿流体,当0<n<1时,则1<a<2;当n>1时,则2<a<2.5.本文n=0.643,a=1.844.
若不计摩擦损失,即压力损失pm=0.又a1= a2,(13)式可写为

式中:uB为无摩擦条件下的伯努利速度。
引入流量修正系数Cd,有

由连续性方程,可知

而压力损失又可表示为

式中:kL为局部损失系数。
结合(13)式、(15)式、(16)式、(18)式和(19)式可求得收缩段处的流量修正系数Cd和局部损失系数kL.如图6所示。
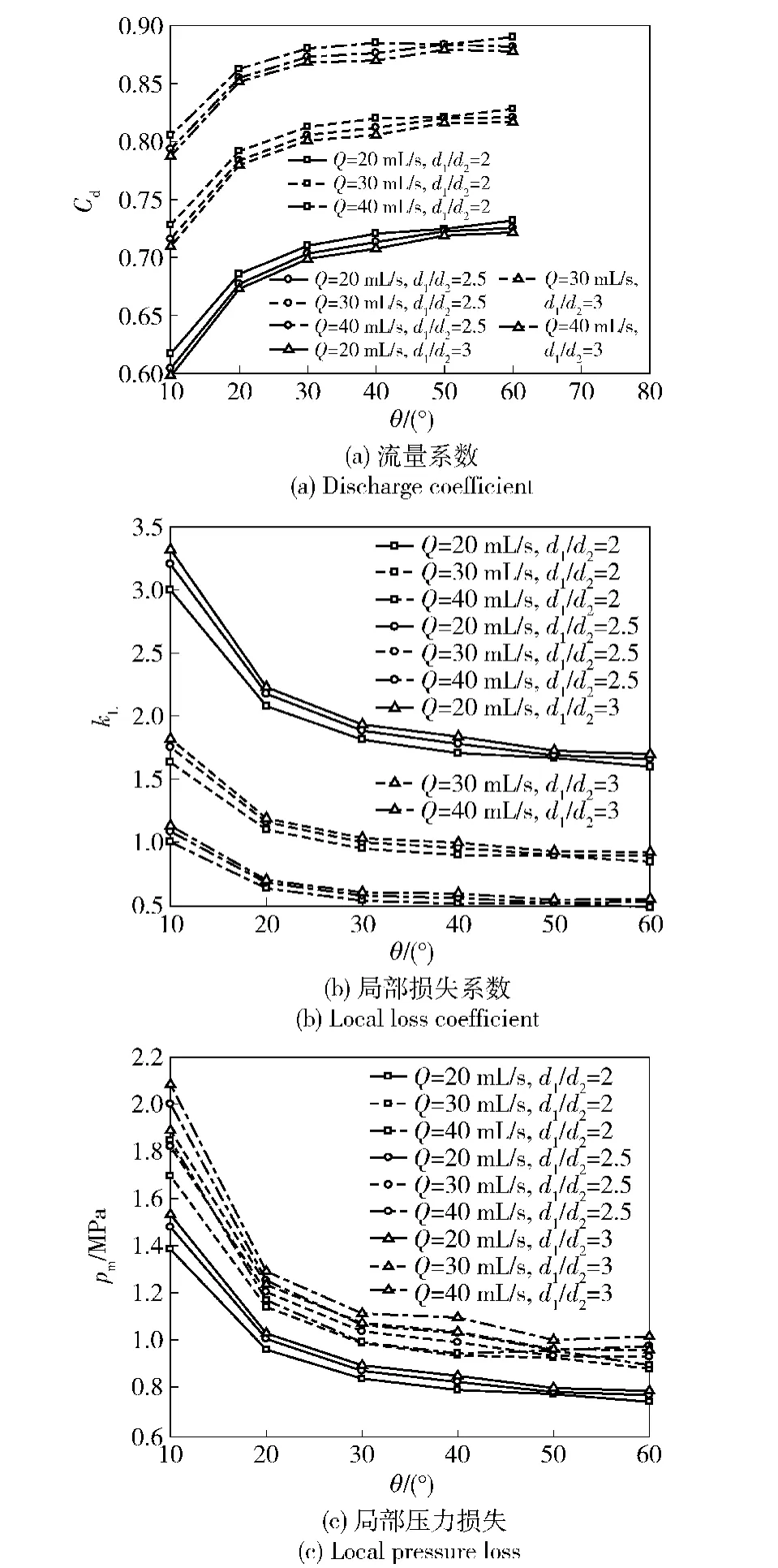
图6 收缩段的流量系数、局部损失系数和局部压力损失Fig.6 Discharge coefficient,local loss coefficient and local pressure loss of the contraction section
由图6可知:1)在相同流量和收缩比下,角度增加,流量系数增加,局部损失系数和压力损失减小,这是因为角度增大,一则减小收缩段长度,二则使收缩段处流体粘度减小,从而使压力损失减小;2)在相同流量和角度下,收缩比增大,流量系数减小,局部损失系数和压力损失增大,这是因为收缩比增大,使收缩段长度增大,从而使压力损失增大;3)在相同收缩比和角度下,流量增大,流量系数增大,局部损失系数减小,而压力损失增大,可见流量增大后,会产生两种趋势:①粘度减小,使压力损失有减小的趋势;②速度增大,使压力损失有增大的趋势。可见第2种趋势更为显著。
3.2流变特性
Mansour等[17]的研究表明,平均表观粘度是表征凝胶推进剂雾化特性的重要参数。平均表观粘度在锥形喷注器内可定义为

求得在流量为30 mL/s,收缩比为3,不同角度下的收缩段及其前后区域各截面的平均表观粘度,如图7所示。图中坐标原点取距离收缩段截面1为L的坐标,两虚线之间为收缩段区域。在收缩角为30°时,锥形喷注器的粘度云图如图8所示。

图7 收缩段处各截面的平均表观粘度Fig.7 Mean shear viscosities of cross sections at contraction section

图8 收缩角度为30°时的粘度图Fig.8 Shear viscosity at contraction angle of 30°
从图7和图8可知,在收缩段上游距离截面1一定距离时,平均表观粘度开始下降,在收缩段区域的降幅显著,在收缩段末端附近平均表观粘度下降到最低值,在截面2之后开始缓慢回升。平均表观粘度最小值在截面2上游L/10附近。因此,在设计锥形喷注器时,应尽量使出口段的长度减小甚至为0,以保证在出口截面处的平均表观粘度为最低值。当收缩角度为50°和60°时,平均表观粘度在截面1处显著回升,这是因为收缩角度增大时,流场在截面1的拐角处存在低速流动区域,此区域附近的表观粘度较大,因而导致平均表观粘度回升。图9为收缩段截面2的平均表观粘度。

图9 收缩段截面2的平均表观粘度Fig.9 Mean shear viscosity of the cross section 2
从图9可知,1)在相同流量和收缩比下,随收缩角度的增大,截面2处平均表观粘度逐渐减小;2)在相同流量和收缩角度下,随收缩比的增大,平均表观粘度变化不大;3)在相同收缩比和收缩角度下,随流量的增大,平均表观粘度逐渐减小。可总结出,影响截面2平均表观粘度变化的主要因素为收缩角度和流量,收缩比对其影响微弱。
结合图6和图9可得,收缩角度越大,收缩段的局部压力损失越小,即消耗供给系统驱动功率越小,且截面2处的平均表观粘度越小,则越有利于凝胶推进剂的雾化。而在图7中,当收缩角度增大到50°和60°时,在截面1处出现低速流动区域,可能会导致凝胶推进剂的堆积现象产生。因此,综合考虑,在设计锥形喷注器时,收缩角度选择在40°左右是较为合理的。
4 弯管的流动特性研究
4.1流阻特性
弯管也是煤油凝胶供给系统中常见的管道之一。其几何结构如图10所示。

图10 弯管的几何结构Fig.10 Geometric structure of elbow pipe
数值计算工况为,弯管管径D=5 mm,流量Q= 20 mL/s,弯径比r/D取1~4,弯管的角度为90°.图 10中截面1、2均缓变流动,不考虑重力,对两截面列伯努利方程为

由u1=u2,a1=a2=1.844,结合数值计算的压力p1、p2,可求出压力损失pm.压力损失可表示为,求得的弯管局部损失系数ζ,如图11所示。
4.5.3 免费开放感知对地方依赖有正向影响 模型结果显示,免费开放对地方依赖为正向影响,以地方依赖为中介的间接影响,进而影响地方认同.地方依赖对地方认同的影响较大,路径系数达到0.93.说明公园绿地免费开放后,对居民更多的是在地方依赖方面,能够使居民感觉到城市公园是生活中不可或缺的一个公共空间,进而形成对地方的认同.
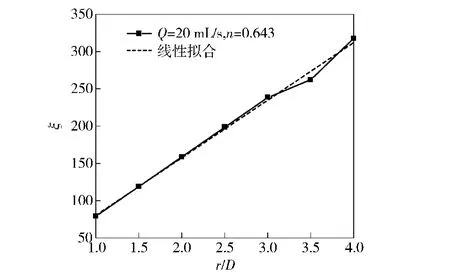
图11 弯管的局部损失系数Fig.11 Local loss coefficient of elbow pipe
由图11可知,弯管的局部损失系数同弯径比呈线性关系,随弯径比的增大而增大。在流量不变时,弯管的压力损失也随弯径比线性增大。拟合方程ζ=78.75(r/D)+3.15.

图12 截面3处的压强分布与二次流速度及其流线Fig.12 Pressure and secondary flow velocity of the cross section 3
流体在弯管内流动时,由于离心力的作用,在弯管的过流截面上,流体的压强将从弯管的内侧到外侧逐渐增大,如图12所示。图12中左侧为弯管内侧,右侧为弯管外侧。
从图12可知,由于离心力的作用,使截面3处的外侧压强大于内侧压强,且中心部分的流体向弯管外侧流动,而外侧的流体则沿管壁流入内侧,产生双涡旋形式的二次流。二次流速度在中心处较大,在管壁和涡旋中心处较小,速度和流线都是对称分布的。二次流将与主流(截面法向流动)结合形成复杂的螺旋流动,造成局部的流动损失。
4.2流变特性
对弯管的流变特性研究主要针对其流动的非对称性特点。煤油凝胶的流动从弯管截面1进入时就开始出现流动的不对称性,并在夹角为45°处的截面表现最为显著,然后逐渐减弱,直至从截面2流出。因此,取截面3为研究对象。此截面在流量为20 mL/s,弯径比为1.0的速度、剪切速率和表观粘度云图,以及其与Oxy平面相交线的速度、剪切速率和表观粘度随弯径比的变化,如图13、图14所示。
从图13和图14可知,截面3的速度、剪切速率和表观粘度都是非对称分布的,且向弯管的内侧偏移。随弯径比的减小,流场的非对称性越显著,速度峰值、剪切速率的最小值和表观粘度峰值向内侧的偏移量增大,速度峰值增大,表观粘度峰值减小,弯管内侧的剪切速率及其梯度大于外侧,可见内侧壁面切应力大于外侧。剪切速率最小值的偏移量与表观粘度的偏移量是一致的,大于速度的偏移量,这说明剪切速率和表观粘度的非对称性比速度的非对称性显著。
5 结论
1)直圆管:流量和管径一定时,沿程阻力损失同管长呈正比;流量和管长一定时,沿程阻力损失同R1+3n呈反比;轴向速度无量纲化后的曲线重合,表明管径相同时,管内“柱塞”流区域分布是固定的。
2)锥形喷注器:平均表观粘度在距离截面2左侧L/10处下降到最低值;设计锥形喷注器时,应使出口段的长度减小甚至为0,保证在出口截面处的平均表观粘度为最低值;影响截面2平均表观粘度变化的主要因素为收缩角度和流量,收缩比对其影响微弱;综合来看,收缩角度选择在40°左右是较为合理的。
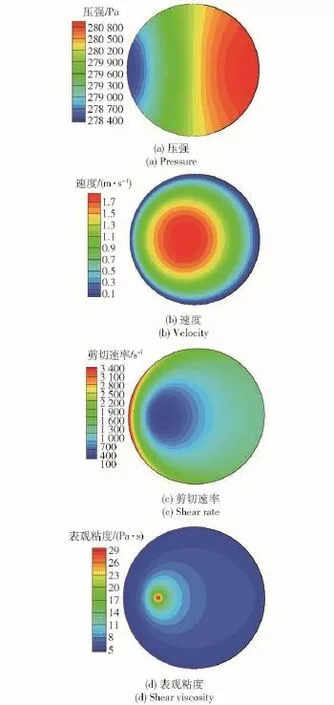
图13 截面3的速度、剪切速率和表观粘度云图Fig.13 Velocity magnitude,shear rate and shear viscosity of the cross section 3

图14 相交线的速度、剪切速率和表观粘度分布Fig.14 Velocity magnitude,shear rate and shear viscosity of the intersection line
(
)
[1]武晓松,陈军,王栋.固体火箭发动机原理[M].北京:兵器工业出版社,2011:337-341. WU Xiao-song,CHEN Jun,WANG Dong.Theory of solid rocket engine[M].Beijing:Publishing House of Ordnance Industry,2011:337-341.(in Chinese)
[2]Kraynik A M,Geller A S,Glick J H.Gelled propellant flow:boundary layer theory for power law fluids in a converging planar channel,SAND89-1720 UC-906[R].Albuquerque,New Mexico:Sandia National Laboratories,1989.
[3]Rahimi S,Natan B.The injection process of gel fuels[C]∥33rd Joint Propulsion Conference and Exhibit.Seattle,WA,US:AIAA,1997.
[4]Rahimi S,Natan B.Flow of gel fuels in tapered injectors[J]. Journal of Propulsion and Power,2000,16(3):103-118.
[5]Natan B,Rahimi S.Numerical solution of the flow of power-law gel propellants in converging injectors[J].Propellants,Explosives,Pyrotechnics,2000,25(4):203-212.
[6]左博,张蒙正.凝胶模拟液直圆管流动特性数值模拟[J].火箭推进,2008,34(5):27-30. ZUO Bo,ZHANG Meng-zheng.Numerical simulation of tube flow characteristics for gel simulation[J].Journal of Rocket Propulsion,2008,34(5):27-30.(in Chinese)
[7]张蒙正,左博.幂律型凝胶推进剂管路中的流动特性[J].推进技术,2009,30(2):246-250. ZHANG Meng-zheng,ZUO Bo.Flow behavior of power law model gelled propellant in the pipe[J].Journal of Propulsion Technology,2009,30(2):246-250.(In Chinese)
[8]强洪夫,夏学礼.凝胶推进剂管道流动特性影响因素数值分析[J].含能材料,2009,17(2):137-141. QIANG Hong-fu,XIA Xue-li.Numerical analysis of factors affecting flow property of gel propellants in round pipes[J].Chinese Journal of Energetic Materials,2009,17(2):137-141.(in Chinese)
[9]Yoon C J,Heister S D.Plain-orifice gelled propellant flow characteristics with rheological hysteresis[C]∥48th AIAA/ASME/ SAE/ASEE Joint Propulsion Conference&Exhibit.Atlanta,Georgia:AIAA,2012.
[10]Kukushkin V,Ivanchenko A.The pasty propellant rocket engines development[C]∥29th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit.Monterey,CA:AIAA,1993.
[11]Yoon C J,Heister S D,Sojka P E.Injector flow characteristics for gel propellant[C]∥47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit.San Diego,Georgia:AIAA,2011.
[12]沈仲棠,刘鹤年.非牛顿流体力学及应用[M].北京:高等教育出版社,1989:47-51. SHEN Zhong-tang,LIU He-nian.Mechanics and application of non-Newtonian fluid[M].Beijing:Higher Education Press,1989:47-51.(in Chinese)
[13]Rahimi S,Natan B.Air-blast atomization of gel fuels[C]∥37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit.Salt Lake City,Utah:AIAA,2001.
[14]Jens V K,Klaus M,Helmut K C.Characteristic flow and spray properties of gelled fluels with regard to the impinging jet injector type[C]∥42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit.Sacramento,California:AIAA,2006.
[15]刘国庆,蔡体敏,夏学礼,等.凝胶推进剂锥形管道流动特性数值分析[J].固体火箭技术,2009,32(2):154-158. LIU Guo-qing,CAI Ti-min,XIA Xue-li,et al.Numerical analysis on flow property of gel propellants in tapered round pipes[J]. Journal of Solid Rocket Technology,2009,32(2):154-158.(in Chinese)
[16]林建忠,阮晓东,陈邦国,等.流体力学[M].北京:清华大学出版社,2013:224-226. LIN Jian-zhong,RUAN Xiao-dong,CHENG Bang-guo,et al.Fluid mechanics[M].Beijing:Tsinghua University Press,2013:224-226.(in Chinese)
[17]Mansour A,Chigier N.Air-blast atomization of non-Newtonian liquid[J].Journal of Non-Newtonian Fluid Mechanics,1995,58(2/3):161-194.
Numerical Research on Flow Characteristics of Kerosene Gel in Different Kinds of Pipeline Based on Power-law Constitutive Model
CAO Qi1,FENG Feng1,WU Xiao-song1,CHEN Chao2
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China;2.Anhui Military Industry Group Holding Co.,Ltd,Hefei 230001,Anhui,China)
In order to optimize the design of kerosene gel supply pipeline and tapered injector,the powerlaw constitutive model is used to build a solution method of two-dimensional/three-dimensional incompressible steady flow.The flow characteristics of kerosene gel are numerically studied based on a SIMPLE algorithm.The analytical solution of parameters of propellant in straight round pipe and the kinetic energy correction coefficient of laminar flow are presented.The results show that the plunger flow area of straight round pipe is fixed when pipe diameter is unchanged.To reduce the average apparent viscosity of the injector outlet cross section,the length of outlet section needs to be decreased.The reasonable contraction angle of injector is about 40°.In elbow pipe,The secondary flow in the form of double vortices exits in elbow pipe.The asymmetries of shear rate and apparent viscosity are more significant than the asymmetry of flow velocity.
ordnance science and technology;kerosene gel;pressure loss;kinetic energy correction coefficient;average apparent viscosity;secondary flow;asymmetry;power-law fluid
V421.4+2
A
1000-1093(2015)02-0242-08
10.3969/j.issn.1000-1093.2015.02.008
2014-04-01
航天科技创新基金项目(CASC03-02);南京理工大学自主科研专项计划项目(30920140112001)
曹琪(1988—),男,博士研究生。E-mail:caoqi_njust@163.com;武晓松(1960—),男,教授,博士生导师。E-mail:nust203@mail.njust.edu.cn

