极大极小随机规划逼近最优值的收敛性

赵礼阳，霍永亮

（1.重庆师范大学数学学院，重庆401331；2.重庆文理学院数学与财经学院，重庆402160）

极大极小随机规划逼近最优值的收敛性

赵礼阳1，霍永亮2

（1.重庆师范大学数学学院，重庆401331；2.重庆文理学院数学与财经学院，重庆402160）

为了研究极大极小随机规划问题最优值的收敛性，先把极大极小随机规划问题转化为二层极小随机规划模型，通过二层极小随机规划模型得到其解的收敛性条件，然后在进一步假设上层原问题有唯一最优解的情况下，得到其逼近问题的最优值上半收敛于原问题的唯一最优值。

随机规划；逼近解；上半收敛

设上层极大随机规划问题的决策变量为x∈Rn，下层问题极小规划的目标函数为是下层极小随机规划问题的决策变量，并且下层极小随机规划问题满足约束条件：对于极大极小随机规划问题，可以转化为二层极小随机规划问题，下层随机规划问题的收敛性反馈到上层随机规划问题，同时得到上层随机规划问题最优值的收敛性。文献［1］中对二层极小随机规划解的收敛性进行了详细的讨论，并得出了相应的结论。文献［2］是研究了随机规划解的稳定性。文献［3-4］研究了随机规划逼近解的收敛性条件。文献［5］研究了随机规划上半收敛性条件。文献［6］在二层极大的数学模型下分析其逼近解的收敛性。本文在文献［1］和文献［4］的基础上，在得到最优解的情况下，进一步研究极大极小问题最优值的收敛性条件。

本文考虑如下极大极小随机规划问题：

原问题（1）等价于下列二层随机规划问题：

其中y为

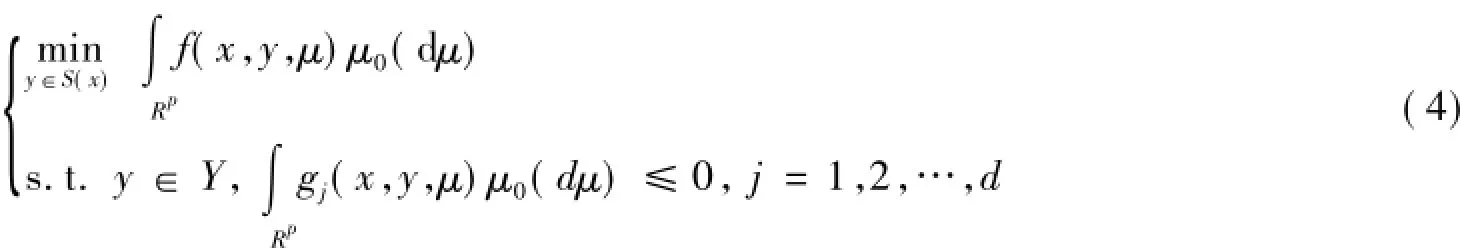
的解。

问题（3）的逼近问题可以写成

其中y为

的解。

本文假定定义域X和Y分别是在Rn和Rm上的紧集，f，g都是定义在Rn×Rm×Rp上的连续有界的函数，μ0=P°ξ-1，μn=P°ξ-1n，ξ是定义在概率空间（Ω，F，P）上面的m维随机向量，ξn为ξ的离散化随机变量序列。

1　下层原问题等价的随机规划解集的收敛性

在讨论上层随机规划问题最优解的收敛性之前，先讨论下层随机规划解的收敛性问题。如果固定x0∈Rn，则原问题的下层随机规划问题的等价命题可以改写成：

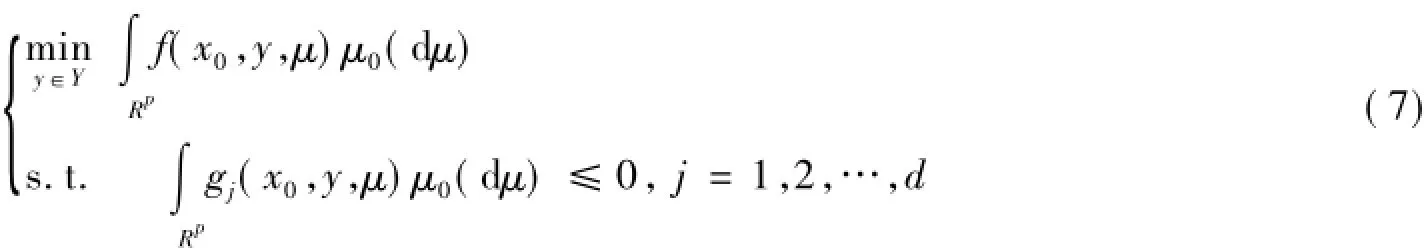
同时，当xn→x0时，其相应的逼近问题可以改写成：

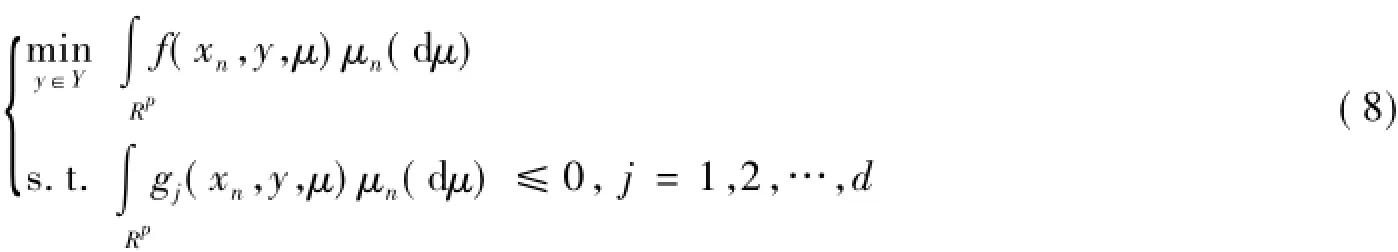
设问题（7）和（8）的可行集为S0（x0）和Sn（xn）。为了讨论的方便，本文把问题（7）和（8）转化为无约束问题（9）和（10）：

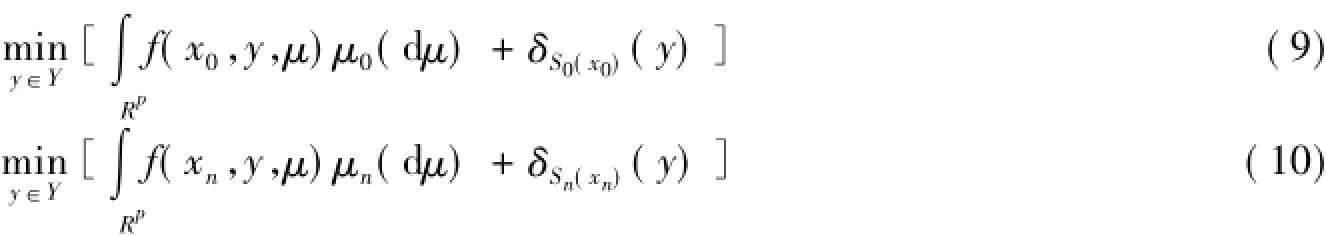
其中δS（y）满足随机规划问题（9）与（10）的最优解集分别设为M0（x0）和Mn（xn）。

定义1［5］称可行集S0（x0）是正则的，即满足S0（x0）=clS0（x0）0，并且S0（x0）0≠φ，其中：

定义2［2］若xn→x0，称集合序列｛Mn（xn）｝上半收敛于M0（x0），即

引理1［1］若xn→x0，且f（x，y，μ）在X×Y×Rp上连续有界，在X×Y×Rp上下半连续且有界，对每个固定的y，gj（x，y，μ）关于（x，μ）上半连续，可行集S0（x0）正则，且μn→μ0，则问题（8）的最优解序列Mn（xn）上半收敛于问题（7）的最优解集M0（x0）。

根据文献［1］的推论2.1可以得到：如果下层问题（7）有唯一最优解，则问题（8）的任意一个最优解yn（xn）∈Mn（xn）连续收敛于问题（7）的唯一最优解y0（x0）。

2　上层原问题等价的随机规划的最优值的收敛性

本文讨论下层问题（7）只有唯一最优解的情况。设问题（7）的最优解为y0（x），问题（8）的任意一个最优解设为yn（x），上层规划原问题的等价解问题可以改写成

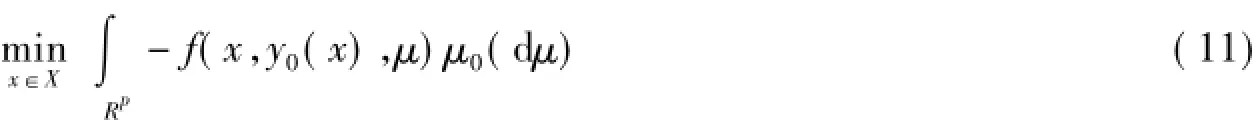
相应的逼近问题可以改写成

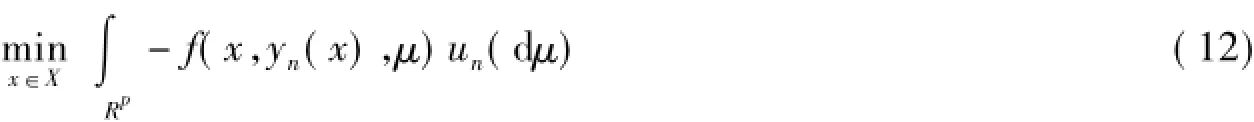
设问题（11）和（12）对应的最优解集为M0和Mn，设A0是问题（11）的优解对应的函数值，An是逼近问题最优解集对应的函数值序列，即，令：

根据文献［1］的定理3.1和文献［2］的定理5.1，有

由文献［1］的定理3.2可得，问题（12）的最优解集序列Mn上半收敛于问题（11）的最优解集M0。

推论1如果x0∈Rn是问题（11）的唯一最优解，那么Mn的任意最优解xn∈Mn都上半收敛于x0。

证明因为Mn上半收敛于M0，又因为M0为单元素集合，则就有Mn中的任意序列xn，有xn→x0。否则有xn→a，且a≠x0，这就与Mn上半收敛于M0相互矛盾。证明完毕。

定理1若xn→x0，且f（x，y，μ）在X×Y×Rp上连续有界，gj（x，y，μ），j=1，2，…，d，在X×Y×Rp上下半连续且有界，对每个固定的y，gj（x，y，μ）关于（x，μ）上半连续，可行集S0（x0）正则，且μn→μ0，如果x0∈Rn是问题（11）的唯一最优解，则有：lim Fn（xn）=F0（x0），即

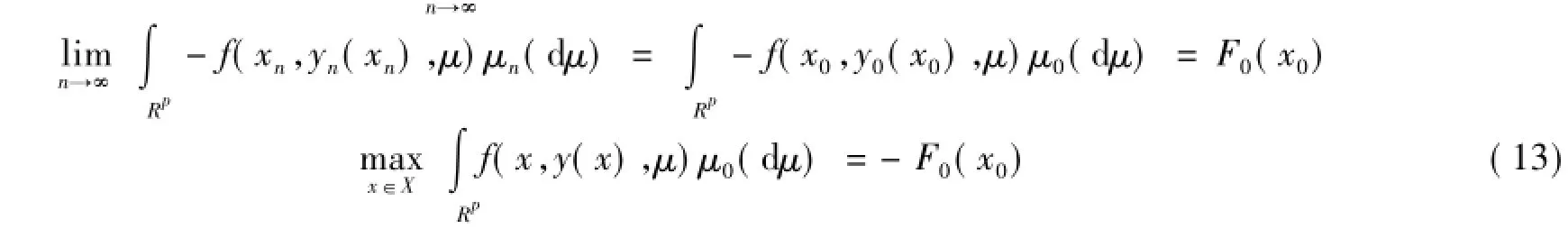
证明因为x0是问题（11）的唯一最优解，故中所有最优解对应的函数值构成的序列为Fn（xn）。由推论1得：Mn中任意序列上半收敛于x0，而f是X×Y×Rp上的连续有界函数，所以必有函数序列∫p-f（xn，yn（xn），μ）μn（dμ）上敛于F0（x0），式（13）显然是成立R的。证明完毕。

［1］周婉娜，霍永亮，吴凡.二层随机规划逼近最优解集的上半收敛性［J］.纯粹数学与应用数学，2014，32（2）：207-215.

［2］霍永亮.随机规划稳定性理论［M］.成都：西南交通大学出版社，2010.

［3］骆建文，鲁世杰.随机规划逼近解的收敛性［J］.浙江大学学报，20007，27（5）：493-497.

［4］霍永亮，刘三阳.随机规划逼近最优解集的上半收敛性［J］.西安电子科技大学学报，2005，32（6）：953-957.

［5］霍永亮.二层随机规划逼近问题最优解集的上半收敛性［J］.系统科学与数学，2014，34（6）：674-681.

［6］刘勇，王慧，徐裕生，等.二层随机规划逼近解的收敛性［J］.纯粹数学与应用数学，2008，24（4）：768-773.

（责任编辑刘舸）

Astringency of Minimax Stochastic Programming Approximation Optimal Value

ZHAO Li-yang1，HUO Yong-liang2
（1.College of Mathematics Science，Chongqing Normal University，Chongqing 401331，China；2.College of Mathematics and Finance，Chongqing University of Arts and Science，Chongqing 402160，China）

In order to study the convergence of the optimal minimax stochastic programming problem value，at first，the minimax problem was transformed stochastic programming into two layers of minimal stochastic programming model，and we obtained the convergence conditions through two layers of minimal stochastic programming model.Then suppose further that the upper primary problem has a unique optimal solution under the condition of the unique optimal approximation，the problem of optimal value of semi converges to the value of the original problem was obtained.

stochastic programming；approximation solution；upper semi-convergence

O175

A

1674-8425（2015）04-0132-04

10.3969/j.issn.1674-8425（z）.2015.04.026

2015-01-15

重庆高校创新团队建设计划项目（KJ301321）

赵礼阳（1990—），男，重庆大足人，硕士研究生，主要从事随机优化解的稳定性研究。

赵礼阳，霍永亮.极大极小随机规划逼近最优值的收敛性［J］.重庆理工大学学报：自然科学版，2015（4）：132-135.

format：ZHAO Li-yang，HUO Yong-liang.Astringency of Minimax Stochastic Programming Approximation Optimal Value［J］.Journal of Chongqing University of Technology：Natural Science，2015（4）：132-135.