非高斯码元检测的马尔可夫链蒙特卡洛算法*
冯士民,周穗华,应文威
非高斯码元检测的马尔可夫链蒙特卡洛算法*
冯士民1,周穗华1,应文威2
(1. 海军工程大学 兵器工程系, 湖北 武汉 430033; 2. 中国人民解放军91635部队, 北京 102249)
针对实际超低频接收机不仅受非高斯噪声的影响,还受接收机内部和外部环境中高斯噪声影响的问题,对噪声采用非高斯分布和高斯分布的混合模型建模,根据混合模型的性质,设计了一种利用马尔可夫链蒙特卡洛方法的超低频信号码元盲检测算法。盲检测算法在贝叶斯层次模型下,采用Gibbs抽样和M-H抽样更新参数,同步估计信道衰落系数和噪声模型参数,并实现对信号码元的检测。算法迭代效率快、精度高。通过与最优检测算法性能比较,盲检测算法性能优异,对超低频信号接收具有重要的现实意义。
非高斯噪声;盲检测;高斯尺度混合;混合模型
(1.DepartmentofWeaponryEngineering,NavalUniversityofEngineering,Wuhan430033,China;
2.ThePLAUnitof91635,Beijing102249,China)
超低频通信系统中,受雷电等产生的大气噪声的影响,噪声往往具有明显的非高斯特性。传统的线性接收机或高斯接收机在非高斯噪声环境下性能急剧恶化,严重影响通信系统的正常工作,为了实现超低频信号码元的最佳检测,需要对噪声进行建模和参数估计。ConteE,BuzziS和LopsM等研究了采用高斯尺度混合(GaussianScaleMixture,GSM)分布模型对噪声建模[1-3],并实现信号码元的检测。但是,实际中的接收机,不仅受到非高斯噪声的影响,同时也会受到接收机内部和外部环境中高斯噪声的影响[4-7]。所以本文在对噪声建模时,采用了GSM分布和高斯分布的混合模型,这对于实际中实现对信号码元的最优检测有更好的适用性。同时,在信号码元检测方法上,采用传统的最大期望算法或最大似然估计设计检测算法[8-10]。由于该模型参数较多,采用上述方法时,概率密度计算难度大,精度也不够理想。马尔可夫链蒙特卡洛(MarkovChainMonteCarlo,MCMC)算法,能够解决具有高维度且形式复杂的未知参数的后验概率计算问题,是一种在统计计算中性能优越的方法[11-12]。通过设计MCMC方法来实现信号码元在混合噪声模型下的盲检测算法,迭代收敛快,精度高,具有明显的优势。
1 噪声模型
1.1 GSM模型
GSM模型是用一个高斯分布变量和一个隐含的尺度随机变量相乘建立的模型,如式(1)所示。
(1)
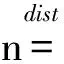
n~N(0,γδ2), γ~IG(μ,λ)
(2)
其中,δ2为高斯分布的方差,μ和λ分别为逆高斯分布的均值和形状参数。通过计算随机变量n的特征函数表达式,得出:
(3)
可以看出,对于同一个分布n,λ,μ和δ2满足特定比例关系,这表明,μ可以归一化到高斯分布方差δ2中。为了更直观地表示,固定参数μ为常数,这与固定逆高斯分布的平均功率为1是一致的。
1.2 噪声模型
为了对噪声进行准确估计并进行信号码元检测,采用高斯尺度混合分布和高斯分布的混合模型作为噪声模型:
p(n)=ω1f(n;δ2,μ,λ)+ω2N(n;0,σ2)
(4)
其中,ω1和ω2为权重因子,满足ω1+ω2=1。
根据1.1节所述性质,可以固定μ=5,则混合模型需要估计的参数为{δ2,λ,σ2,ω},ω={ω1,ω2}为二维向量。
对于噪声数据集N={ni,i=0,1,…,N},引入标签变量Z={zi,i=0,1,…,N}对ni进行分组,其中zi的取值为:当ni属于高斯尺度混合分布时,zi的取值为1;当ni属于高斯分布时,zi的取值为2。zi为独立随机变量,并且满足
p(zi=j)=ωj(j=1,2)
(5)
根据式(3)、式(4)和式(5),可以得出噪声数据集的等效表达式:
(6)
2 信号码元检测模型
2.1 接收信号模型
建立平坦衰落信道下的超低频信号码元接收模型,基于以下3点假设:①假设信号码元在超低频频段上进行传输;②信道中的噪声为加性、混合模型噪声;③信道是平坦衰落的,并假设在处理时间窗内衰落系数不变。
设S1,…,SN为发射的信号码元,每个信号码元采样M次,即Si=[si1,…,siM]T为M维向量。当采用二进制相移键控(BinaryPhaseShiftKeying,BPSK)调制时,sij∈{1,-1}。根据上述讨论,接收模型可以表示为:
Xi=aSi+Ni(i=1,…,N)
(7)其中,a为信道衰减系数,M维向量Xi=[xi1,…,xiM]T为接收到的信号码元,Ni=[ni1,…,niM]T为噪声,根据假设③,在每次处理窗口期间a是固定的,噪声的采样值服从1.2节混合模型的分布,并满足独立同分布,则结合式(6)、式(7),xij满足:
(8)
2.2 贝叶斯层次模型
贝叶斯推断通过先验分布来推断后验分布:
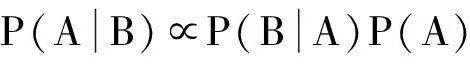
(9)
根据贝叶斯层次理论,可以得出参数集变量{a,δ2,λ,σ2,ω,Z,S}的后验分布为:
(10)
对上述参数选取先验分布时,若参数存在共轭先验分布,则优先选取共轭先验分布:
参数a的共轭先验分布为高斯分布:a~N(κ,ε2)。参数1/δ2的共轭先验分布为伽马分布:1/δ2~Γ(α,β)。参数λ的先验分布为伽马分布:λ~Γ(ξ,τ)。参数1/σ2的共轭先验分布为伽马分布:1/σ2~Γ(g,h)。参数ω的共轭先验为对称狄利克雷分布:ω~D(η,η)。对于信号码元Si,通常认为发射端各个信号码元的发射概率相同,所以取先验分布:
(11)
为了直观表述参数之间的关系,画出模型参数的直接非循环图,如图1所示。
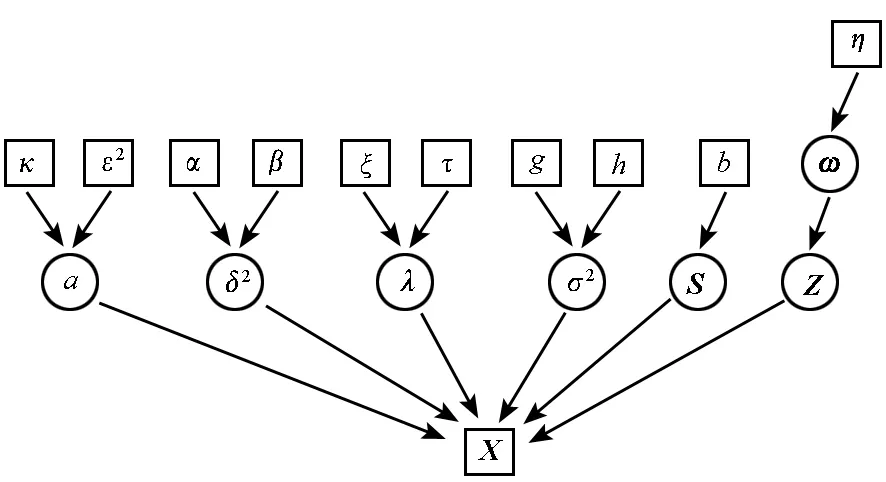
图1 噪声模型参数的直接非循环图Fig.1 Direct acyclic graph specific to the parameters of the noise model
图1中圆圈代表参量,是需要估计的值,方框代表定值。设θ={a,δ2,λ,σ2},θ的超参数为φ={κ,ε2,α,β,ξ,τ,g,h},则式(10)可以扩展为:
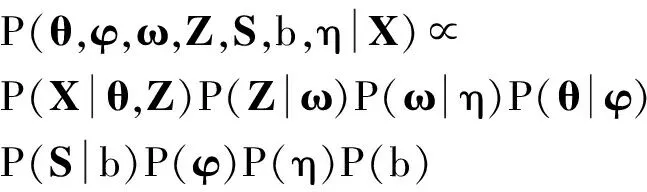
(12)
3 盲检测算法设计
盲检测算法根据混合模型的性质,采用MCMC算法实现信号码元的盲检测。在MCMC算法中,常采用Gibbs抽样和Metropolis-Hasting(M-H)抽样算法对更新参数进行抽样。本文中,对于存在共轭先验分布的参数采用Gibbs抽样算法,对不存在共轭先验分布的参数采用M-H抽样算法。算法在t步的流程如下:
步骤1:通过Gibbs抽样更新参数ω。
ω的后验分布仍服从狄利克雷分布:
(13)
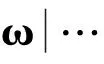
步骤2:通过Gibbs抽样更新参数a。
衰减系数a的后验分布仍服从高斯分布:
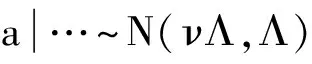
(14)
其中
(15)
(16)
通过Gibbs抽样,生成新的高斯分布随机数对a进行更新。
步骤3:通过Gibbs抽样更新参数δ2。
1/δ2的后验分布为:
(17)
通过Gibbs抽样,生成新的伽马分布随机数对δ2进行更新。
步骤4:通过Gibbs抽样更新参数σ2。
1/σ2的后验分布为:
(18)
通过Gibbs抽样,生成新的伽马分布随机数对σ2进行更新。
步骤5:通过M-H算法更新参数λ。
λ的后验概率为:
(19)
因为λ的后验概率复杂,不是常见的分布,所以通过M-H抽样算法更新λ值,算法步骤如下:
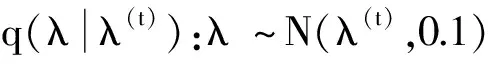
(b)从(a)中抽样λ′作为备选值;
(c)从均匀分布中生成随机数u~U(0,1);
(d)计算新值的接受概率R=min(1,A),其中:
(20)
(e)若u≤R,则接受新值λ(t+1)=λ′,否则不接受新值,则λ(t+1)=λ(t)。
步骤6:更新标签变量Z。
zij的后验概率为:
(21)
(22)
步骤7:通过M-H算法更新变量{γij}。
由于观测数据只有一部分属于高斯尺度混合分布,所以仅更新对应这部分的γij,γij的后验概率为:
(23)
(a)γij选用建议分布为:γij~IG(5,λ);
(c)从均匀分布中生成随机数u~U(0,1);
(d)计算新值的接受概率:
(24)

步骤8:通过Gibbs采样更新信号码元Si。
信号码元Si的后验概率为:
(25)
(26)
算法在t+1步时,采用t步更新过的模型参数,重复上述8个步骤进行新一次的更新,直至各参数收敛。参数收敛后的每次采样值就可以看作目标分布的采样值,这部分采样值的平均值就可以作为参数的估计值。
4 试验及验证
4.1 模型验证
图2为实测的大气噪声数据,用本文的算法参数估计部分对噪声进行参数估计,设置μ=10,估计出的参数值为δ2=26.71,λ=1.60,σ2=6.88,ω={0.04,0.96}。图3为用实测的大气噪声数据和估计参数画出的幅度概率分布(AmplitudeProbabilityDistribution,APD)曲线,从图中可以看出,估计参数画出的APD曲线与实测的噪声数据吻合的很好,平均相对误差小于0.2%,说明了本文的模型对接收机中实际噪声的适用性。
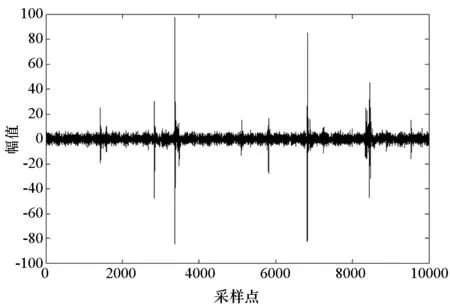
图2 实测大气噪声数据Fig.2 The actual noise data of the receiver
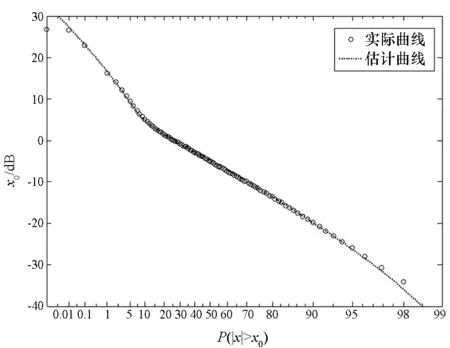
图3 实测噪声数据和估计参数下噪声的APD曲线Fig.3 Amplitude probability distribution graph of the actual noise and noise with estimation parameters
4.2 参数估计
将混合模型的参数设置为δ2=2,λ=2,σ2=0.5,ω={0.2,0.8},a=0.6,仿真数据数目设为N=2000,每个信号码元采样次数M=10。超参数简单地设置为κ=1,ε2=1,α=0.5,β=1,ξ=2,τ=1,g=0.5,h=1,b=0.5,η=0.5。设置算法的迭代次数为800,前200次为废弃数据长度。仿真的结果如图4~8所示,因为ω1=1-ω2,所以只给出ω2的迭代收敛图。
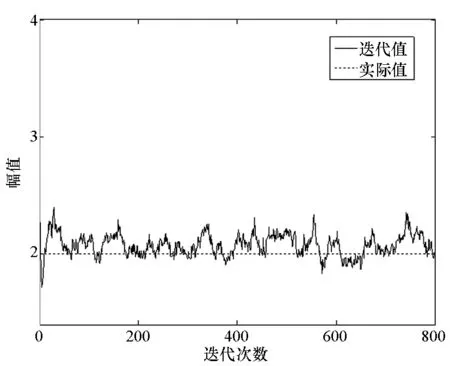
图4 δ2的迭代收敛图Fig.4 Time-average convergence of δ2
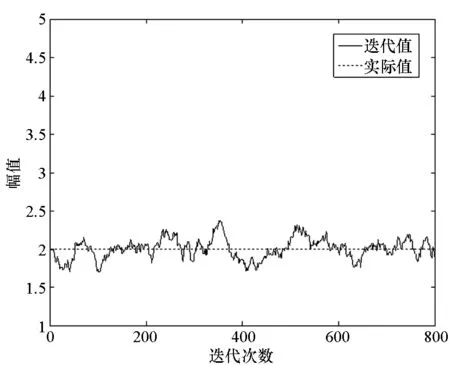
图5 λ的迭代收敛图Fig.5 Time-average convergence of λ
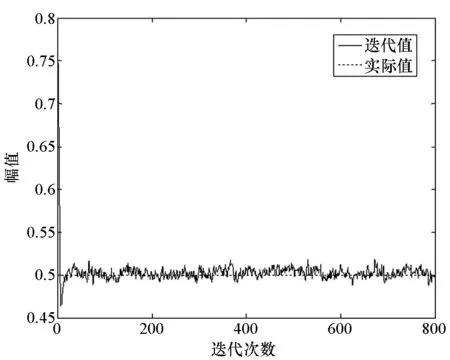
图6 σ2的迭代收敛图Fig.6 Time-average convergence of σ2
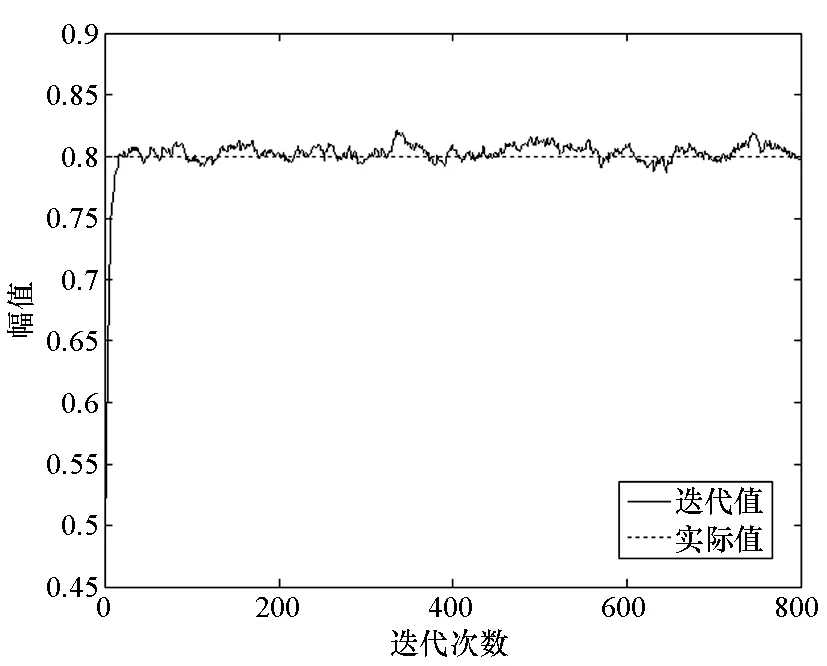
图7 ω2的迭代收敛图Fig.7 Time-average convergence of ω2
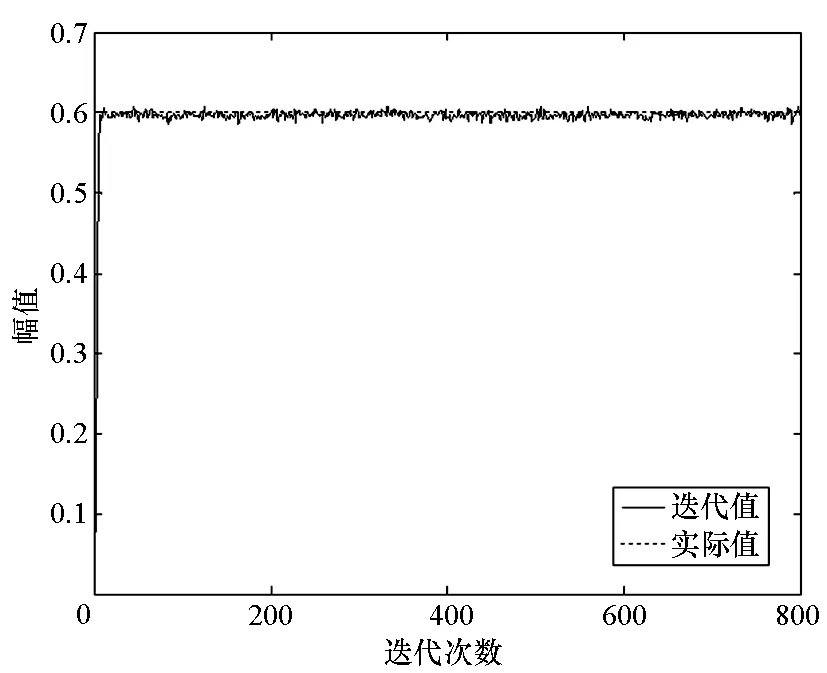
图8 a的迭代收敛图Fig.8 Time-average convergence of a
从各参数的迭代收敛情况可以看出,在进行30次迭代后,各参数就收敛到实际值附近。对后600次的迭代值进行平均,得到各参数的估计结果为δ2=2.18,λ=2.02,σ2=0.50,ω={0.19,0.81},a=0.60。由于更新参数δ2和λ的过程中,采用了M-H算法,所以其迭代数据方差大,但均值仍然与实际值相符合。
4.3 误码率测试
为了测试盲检测算法的性能,对最优检测和盲检测算法的误码率进行比较。最优检测为已预知模型的准确参数,然后对信号码元进行检测。基于逆高斯分布的高斯尺度混合模型的二阶矩为μδ2,高斯分布的方差为σ2,所以总的噪声功率为ω1μδ2+ω2σ2,由此噪声功率来定义信噪比。
图9为不同ω值下,盲检测算法和最优检测的误码率性能比较。从图中可以看出:①在ω值固定的条件下,盲检测算法的性能在较高信噪比下都能逼近最优检测的性能,随着信噪比的降低,较最优检测性能略有下降。②对于相同的信噪比,ω2的值越小,盲检测算法的性能也随着降低,这是因为,ω2的值越小,即非高斯噪声部分的能量越大,使得局部时段信噪比降低很多,从而导致误码率提高。③在信噪比很低的情况下,由于整个时段的信噪比都很低,所以ω2值不同对算法性能的影响不是很明显。
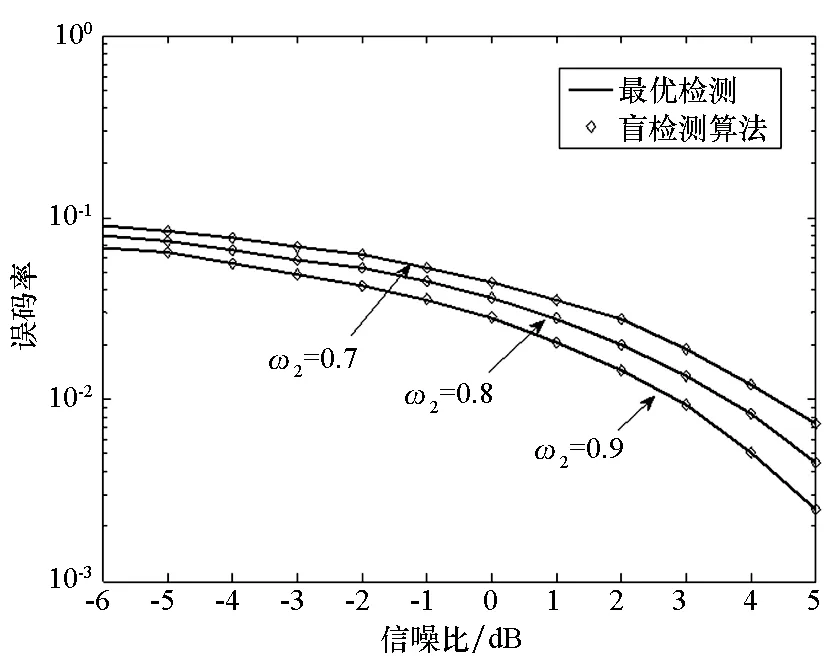
图9 不同ω值下盲检测算法的误码率性能Fig.9 Performance of the blind detection algorithm with different parameter ω
图10为不同过采样率M下,盲检测算法和最优检测的误码率性能比较。如图10所示:无论过采样率M取值为多少,盲检测算法的误码率性能在较高信噪比下都逼近最优检测的误码率性能,随着信噪比的降低,较最优检测性能略有下降;随着M值变大,盲检测算法的误码率变低,并且低信噪比情况下比高信噪比情况下,M值对误码率的影响较大。
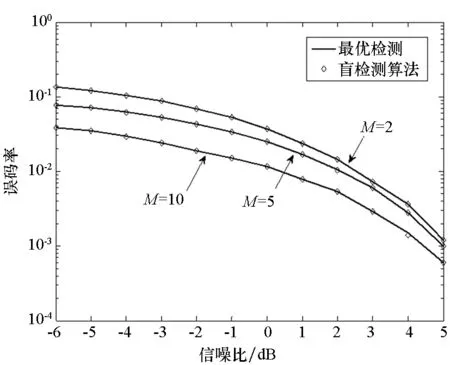
图10 不同过采样率下盲检测算法的误码率性能Fig.10 Performance of the blind detection algorithm with different oversampling rates
5 结论
根据实际超低频接收机中噪声的特点,对噪声采用GSM分布和高斯分布的混合模型建模,在贝叶斯层次模型下,采用MCMC算法,通过Gibbs抽样和M-H抽样,同步估计信道衰落系数和噪声模型参数,并对信号码元进行检测。通过对实测噪声数据分析,说明该模型对接收机中实际接收的噪声有很好的适用性。对算法性能进行仿真分析,结果表明,MCMC算法迭代效率和精度高。在不同噪声模型参数ω和过采样率M下,盲检测算法的性能在高信噪比下都逼近最优检测的性能,对超低频非高斯噪声下信号接收有实际的意义。本文算法有以下创新点:①对噪声采用GSM分布和高斯分布的混合模型建模,符合实际接收机中的噪声特点,对实际装备应用有现实意义和优势;②充分利用GSM分布的性质,将GSM分布等价为条件高斯分布设计MCMC算法,使算法的迭代效率快、精度高。
References)
[1]ConteE,DiBisceglieM,LopsM.Optimumdetectionoffadingsignalsinimpulsivenoise[J].IEEETransactionsonCommunications,1995,43(2/3/4):869-876.
[2]BuzziS,ConteE,LopsM.Optimumdetectionoverrayleigh-fading,dispersivechannels,withnon-Gaussiannoise[J].
IEEETransactionsonCommunications,1997,45(9):1061-1069.
[3]BuzziS,ConteE,LopsM.Signaldetectionoverrayleigh-fadingchannelswithnon-Gaussiannoise[J].IEEProceedingsCommunications,1997,144(6):381-386.
[4] 应文威, 蒋宇中, 刘月亮. 大气低频噪声混合模型的MCMC参数估计[J]. 系统工程与电子技术, 2012, 34(6): 1241-1245.
YINGWenwei,JIANGYuzhong,LIUYueliang.ParametersestimationformixturemodelofatmosphericnoisethroughMCMCmethod[J].SystemsEngineeringElectronics, 2012, 34(6): 1241-1245. (inChinese)
[5]YingWW,JiangYZ,LiuYL,etal.Anoveladaptivereceiverforflatfadingchannelswithimpulsivenoise[C]//ProceedingsofIEEE12thInternationalConferenceonComputerInformationTechnology, 2012: 631-634.
[6]OllilaE,TylerDE,KoivunenV,etal.Compound-Gaussiancluttermodelingwithaninversegaussiantexturedistribution[J].IEEESignalProcessingLetters, 2012, 19(12): 876-879.
[7]GrecoM,GiniF,DianiM.RobustCFARdetectionofrandomsignalsincompound-Gaussianclutterplusthermalnoise[J].IEEProceedingsRadar,SonarNavigation, 2001, 148(4): 227-232.
[8]WangJ,DogandzicA,NehoraiA.Maximumlikelihoodestimationofcompound-Gaussiancluttertargetparameters[J].IEEETransactionsonSignalProcessing, 2006, 54(10): 3884-3898.
[9] 赵宜楠, 李风从, 尹彬. 严重拖尾复合高斯杂波中目标的自适应极化检测[J]. 电子与信息学报, 2013, 35(2): 376-380.
ZHAOYinan,LIFengcong,YINBin.Adaptivepolarimetricdetectionoftargetsinheavy-tailedcompound-Gaussianclutter[J].JournalofElectronics&InformationTechnology, 2013, 35(2): 376-380. (inChinese)
[10]BalleriA,NehoraiA,WangJ.Maximumlikelihoodestimationforcompound-Gaussianclutterwithinversegammatexture[J].IEEETransactionsonAerospaceElectronicSystems, 2007, 43(2): 775-779.
[11]GengP,HuangZT,WangFH,etal.SinglechannelblindsignalseparationwithBayesian-MCMC[C]//ProceedingsofInternationalConferenceonWirelessCommunications&SignalProcessing,IEEE, 2009: 1-4.
[12]LeeA,YauC,GilesMB,etal.OntheutilityofgraphicscardstoperformmassivelyparallelsimulationofadvancedMonteCarlomethods[J]JournalofComputationalGraphicalStatistics, 2010, 19(4): 769-789.
Symbol detection algorithm in non-Gaussian noise using Markov chain Monte Carlo method
FENG Shimin1, ZHOU Suihua1, YING Wenwei2
Consideringthatthereceiverwasnotonlyaffectedbythenon-GaussiannoisebutalsoaffectedbyitsinternalandexternalenvironmentofGaussiannoise,amixedmodelcomposedbynon-GaussiandistributionplusGaussiandistributionwasproposed.AblinddetectionalgorithmbasedonMarkovChainMonteCarlomethodwasdesignedaccordingtothepropertiesofthemixedmodel.Theblinddetectionalgorithmcouldestimatethechannelfadingcoefficient,parametersofnoisemodelandcoulddetectsignalelement.DetectsignalsbasedonBayesianhierarchicalmodelwasusingGibbssampleandM-Hsampleforparameterupdating.Thealgorithmhasahighiterativeefficiencyandprecision.Resultsshowthattheproposedblinddetectionalgorithmperformsaswellastheoptimaldetectionalgorithmandhasimportantrealisticsignificanceinsuperlow-freguencysignalreception.
non-Gaussiannoise;blinddetection;Gaussianscalemixture;mixedmodel
2014-08-29
国家自然科学基金资助项目(51109215)
冯士民(1986—),男,河北石家庄人,博士研究生,E-mail:fengshimin_86@126.com;周穗华(通信作者),男,教授,博士,博士生导师,E-mail:zhousuihua@hotmail.com
10.11887/j.cn.201504019
http://journal.nudt.edu.cn
TN
A

