空腔噪声非线性数值模拟*

王一丁，陈滨琦，郭 亮，钟范俊，童明波

空腔噪声非线性数值模拟*

王一丁1，陈滨琦1，郭 亮2，钟范俊2，童明波1

(1.南京航空航天大学 航空宇航学院， 江苏 南京 210016； 2.成都飞机设计研究所， 四川 成都 610091)

将雷诺平均N-S方程与非线性噪声求解方法相结合，对M219空腔在Ma=0.6，Ma=0.85,Ma=1.35条件下进行了气动噪声分析。通过雷诺平均N-S方程求解空腔流场，得到包含空腔平均流场基本特征以及强制设定的湍流脉动统计描述的初始湍流统计平均解，采用非线性噪声求解方法重构噪声源并高精度模拟压力脉动的传播。通过与试验结果对比表明非线性噪声求解方法能够较好地捕捉空腔流动中的压强脉动及噪声水平。与分离涡模拟方法相比，非线性噪声求解方法在保持计算精度的同时大大减少计算网格，对内埋弹舱快速设计具有一定的参考意义。

空腔；非线性；噪声源；湍流;内埋弹舱

(1.CollegeofAerospaceEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China;

2.ChengduAircraftDesignandResearchInstitute,Chengdu610091,China)

空腔结构广泛存在于飞行器中，新一代战斗飞行器使用内埋弹舱能够使飞行器的阻力最大降低30%，雷达横截面最低可达0.07～0.12m2[1]。内埋弹舱给飞行器带来了隐身、超声速巡航等益处，但同时也产生了一系列复杂的空气动力学问题，包括剪切层极不稳定、边界层分离、激波边界相互干扰等[2-3]，这加剧了空腔内的非定常效应，由此产生的气动噪声将对飞行器的性能与安全产生影响，严重时将导致飞行器产生灾难性的后果。因此对于空腔气动噪声的研究具有重大而紧迫的现实意义。

Le等[4]采用大涡模拟方法(LargeEddySimulation，LES)、Allen等[5]采用分离涡模拟(DetachedEddySimulation，DES)以及Peng等[6]采用混合雷诺平均大涡模拟(Reynolds-AveragedNavier-Stokes/LES，RANS/LES)对空腔噪声进行了数值模拟研究。但对于工程实际问题，这些方法存在计算网格数量大、计算时间长等缺点。目前噪声领域常用的DES方法经常与有限传输算法结合使用，增加了亚格子尺度模型的耗散，有可能导致有效粘度过大，同时统计学湍流能量的传输也存在很大困难，这极大地限制了DES方法适用的流动及网格类型。

Batten等于2002年提出了一种非线性噪声求解(NonlinearAcousticSolver,NLAS)方法，该方法通过对湍流物理量进行重构兼顾了亚格子尺度声源的影响，在保持计算精度的同时降低了网格需求[7-9]。王一丁等将NLAS方法引入内埋弹舱噪声预测中，计算了英国QinetiQ公司M219空腔[10]，空腔计算条件为Ma=0.6，Ma=0.85，Ma=1.35，将NLAS仿真结果与试验数据以及Allen[5]使用DES方法计算结果进行了对比，验证了NLAS方法用于空腔噪声预测的有效性与准确性。NLAS方法计算网格数相对DES方法大幅减少，降低了计算成本，具有一定的工程应用价值。

1 数值方法

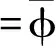
(1)

式中，

(2)

(3)

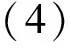
忽略密度脉动项，对以上方程取时间平均可得：

(5)

(6)

式中，Ri是标准雷诺应力张量和湍流热通量相关项。求解噪声的关键是通过RANS计算求得到这些未知项，不能求解的小尺度量则通过RANS计算得到的湍流统计结果重构出来，以此生成亚格子源项。Batten提出的湍流重构方法为：

(7)

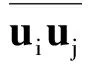
(8)

2 计算模型

2.1 腔体构型

M219模型为典型的开式空腔，在QinetiQ风洞进行了一系列风洞试验，腔体长深比L/D=5，宽深比W/D=1.0。图1为腔体在DERA风洞试验的照片，图2为M219空腔风洞试验件构型图。

图1 M219空腔在DERA风洞噪声试验Fig.1 Noise test of M219 cavity in wind tunnel

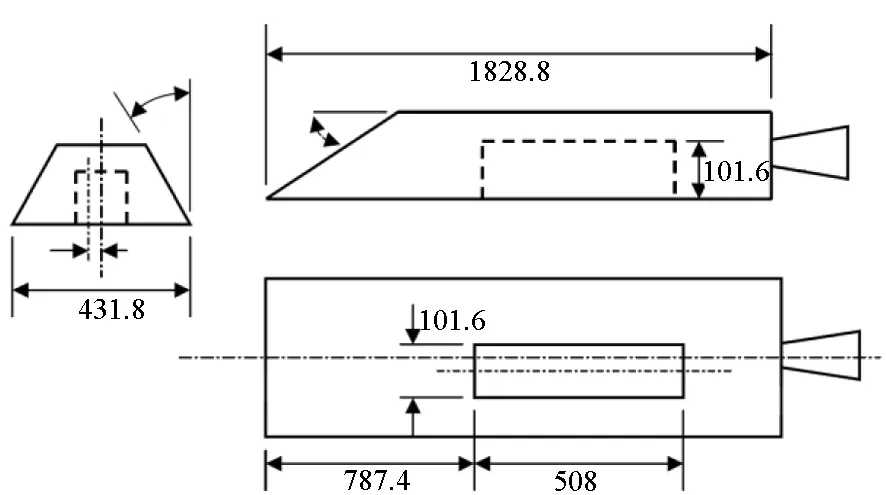
图2 M219空腔风洞试验件构型图Fig.2 Sketch of M219 wind tunnel test pieces

2.2 计算网格

图3为RANS计算网格区域，整个计算域由4个结构块组成，来流方向(x)从-8D到12D，展向从-2D到2D，壁面法向方向从-1D到4D。为了更好地模拟湍流脉动的统计平均结果，RANS计算应采用非线性的各向异性湍流模型，选取cubick-epsilon模式,该模式通过矩阵近似各个位置对涡粘系数的影响，更加符合物理本质。流场物面第一层网格尺度为5×10-2mm，网格数量为260万，基于空腔深度的雷诺数Re=7×106。RANS求解的超声速时来流为固定超声速来流入口条件，远场为特征线条件，出口边界不指定，由内层网格物理量推得。亚声速时来流入口、远场及出口位置均采用特征线边界条件。

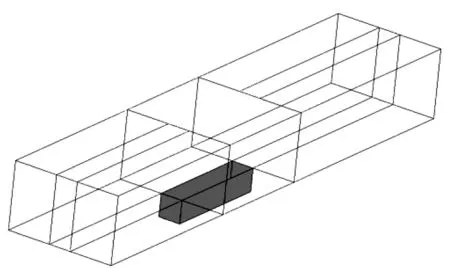
图3 RANS计算区域Fig.3 Computational domain of RANS

噪声计算采用单独的计算网格，物面边界为黏性无滑移绝热壁，采用壁面函数法求解保证物面区域求解精度。RANS计算得到当地雷诺应力张量和热通量的统计平均值，将它插值到噪声计算网格，根据这一统计平均结果对湍流进行人工重构。NLAS方法的优势在于噪声求解器可以在各项同性更好的网格单元上进行计算，特别是在近壁面区域。在进行噪声计算时，计算域选取为包含噪声源周边的区域。图4为RANS计算得到的最大湍流动能kmax的10%等值面，这部分区域是湍流脉动最为剧烈区域、也是主要的噪声源区域、噪声网格重点关注区域。新的边界被设置为吸收层边界，它的远场及衰减层数据由之前RANS计算提供。

图4 RANS计算10% kmax等值面(背景为来流速度)Fig.4 Iso-surface of 10% kmax calculated by RANS(shaded with streamwise velocity)

由于近壁面网格要求放宽以及计算域的缩小，噪声计算网格数量为120万，较RANS计算的260万网格有了显著减少。RANS与NLAS计算的网格对比如图5所示。

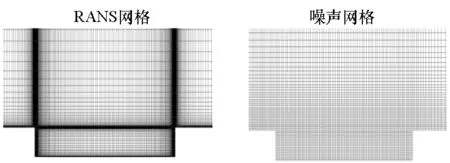
图5 RANS网格与噪声计算网格对比Fig. 5 Comparison of RANS and acoustics meshes

RANS计算控制方程采用有限体积法求解，无黏项采用二阶精度TVD格式离散，黏性项采用中心差分格式离散，时间推进采用隐式方法。NLAS计算空间和时间离散格式与RANS计算相同，时间步长Δt=2×10-5s，共计算20 000步。

来流马赫数与M219风洞试验一致，取Ma=0.6，Ma=0.85，Ma=1.35，覆盖了亚、跨、超声速以充分验证NLAS方法在各种来流条件下模拟空腔噪声的有效性与准确性。在空腔底面中心线处设置10个点记录压力的变化，分别表示为K20～K29，具体位置如图6所示。

图6 脉动压力监测点位置Fig.6 Monitoring locations of oscillating pressure

计算使用4个计算机节点，每个计算机节点包含1个8核2.6GHz处理器和24G内存。

3 计算结果对比分析

空腔底部监测点压强均方根是测量脉动压力的常用指标。图7～9为Ma=0.6，Ma=0.85，Ma=1.35条件下由NLAS方法计算得到的压强均方根值与QinetiQ风洞试验值以及Allen等[5]采用DES方法计算的结果对比。

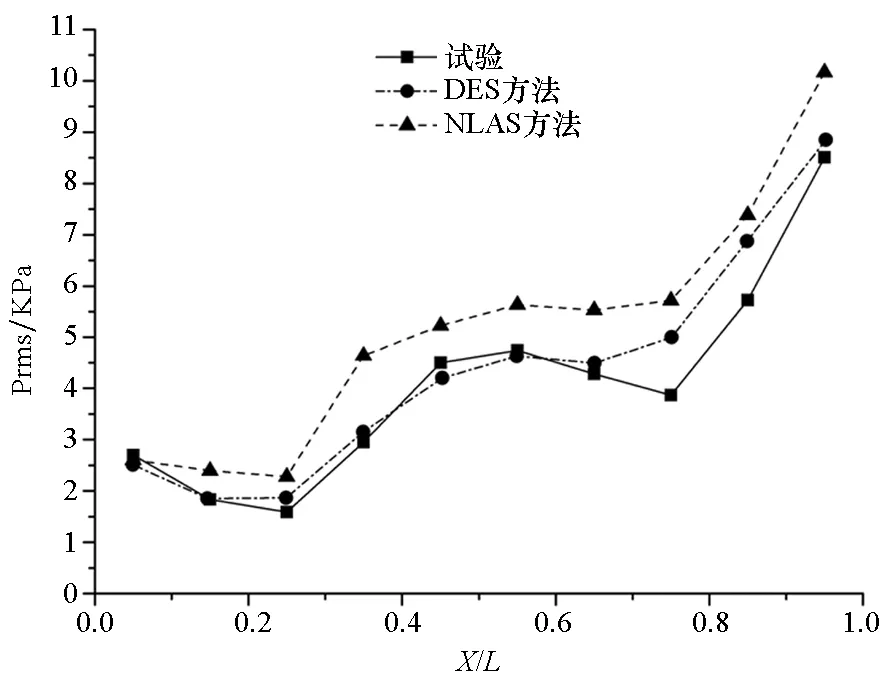
图9 Ma=1.35压强均方根试验、DES及NLAS对比图Fig.9 Comparison of prms between experiment, DES and NLAS at Ma=1.35

通过图7～9可以看到NLAS计算得到的均方根值略大于试验值，与DES方法计算值精度基本相当。而NLAS方法所用网格数量仅为120万，DES方法所用网格数量为260万，在保证计算精度的同时，NLAS方法大大减少了网格需求，缩短了计算时间。

x方向

y方向

z方向图10 NLAS方法得到的涡量分量瞬时等值面Fig.10 Instantaneous streamwise vorticity iso-surfaces calculated by NLAS

图10为空腔在Ma=0.85下x，y，z方向涡量瞬时等值面，涡量相同均为6×103，背景代表流向速度。

对于长深比L/H=5的开式空腔，来流气体流经前缘时，因为腔体深度较大，气流未触及空腔底部，剪切层跨越空腔中部与后壁发生碰撞，空腔前部和中部受剪切层影响较小，压力不会发生大的变化，空腔后部压力上升，对于超音速流动，会诱发激波产生。空腔的流动特性以及腔内复杂的流动环境会导致空腔后部发生颤振，从而产生噪声。噪声通过腔内循环气流传播到空腔前缘，导致剪切层分离，当满足一定相位条件时，形成声波反馈循环，发生腔内自持振荡。

图11～13分别为Ma=0.6，Ma=0.85，Ma=1.35下，位于空腔底部中心线X/L=0.25，X/L=0.55，X/L=0.95三个监测点NLAS仿真得到的声压频谱曲线与试验值对比图。由于压力脉动值在计算起始的一段时间内不具有周期性，而在该段时间之后压力脉动呈现出一定的周期特性并一直保持下去，而这正是所需要的压力脉动数据，也是噪声传播对应的数据。为了防止起始时间的不规则压力脉动影响噪声求解，将起始段的压力脉动截掉，使用0.1s～0.4s的脉动数据。

(a) K22(X/L=0.25)

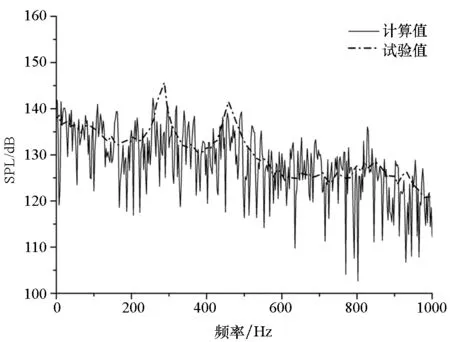
(b) K25(X/L=0.55)

(c) K29(X/L=0.95)图11 Ma=0.6监测点声压频谱特性计算与试验对比Fig.11 Comparison of spectrum between calculation and test at Ma=0.6

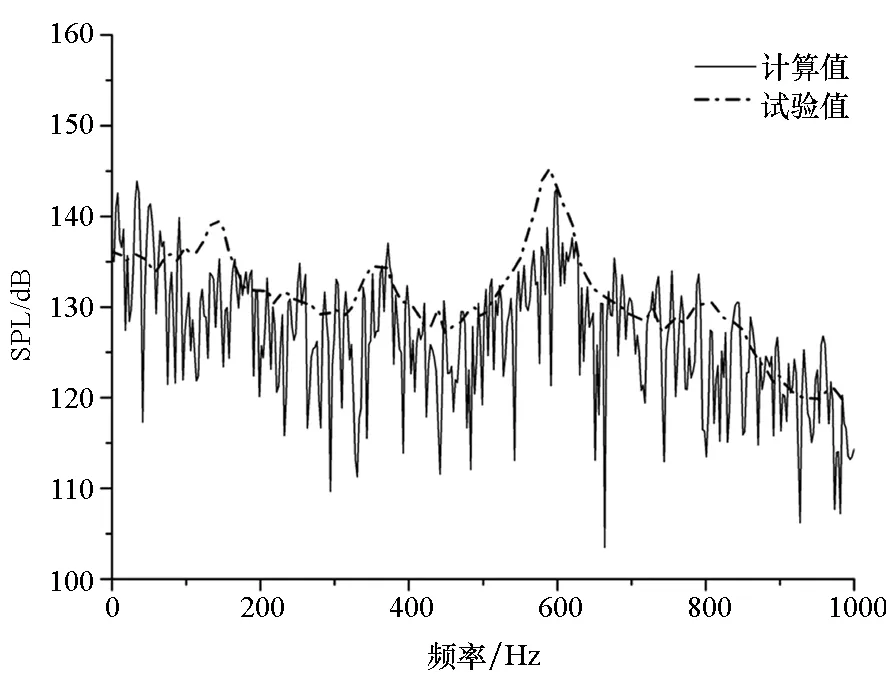
(a) K22(X/L=0.25)

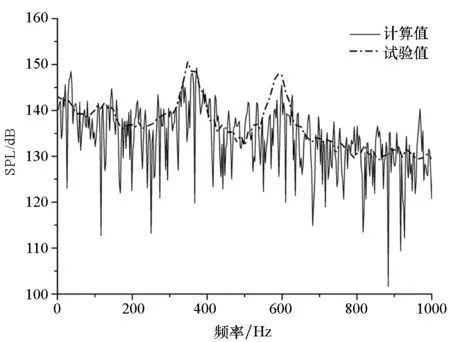
(b) K25(X/L=0.55)

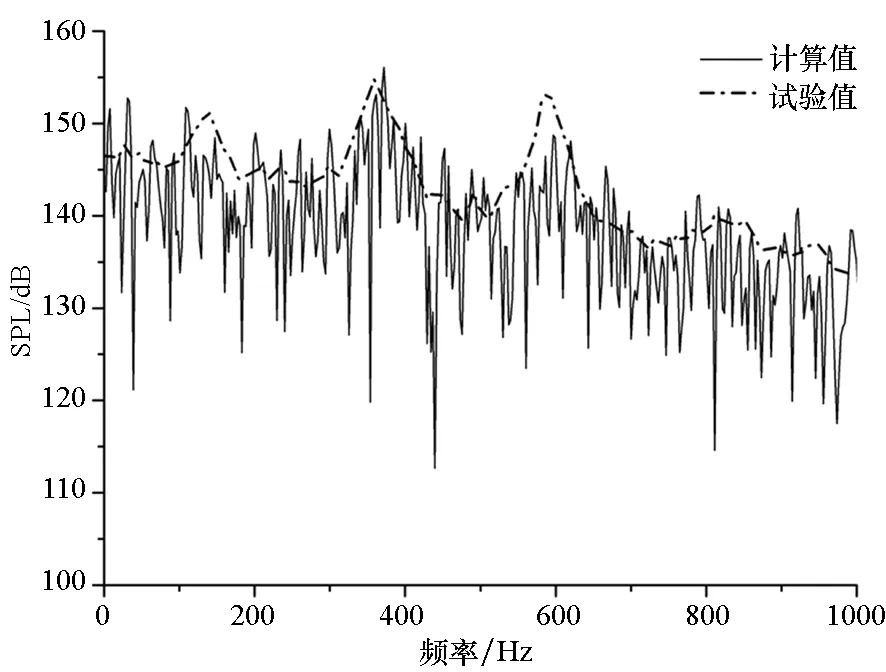
(c) K29(X/L=0.95)图12 Ma=0.85监测点声压频谱特性计算与试验对比Fig.12 Comparison of spectrum between calculation and test at Ma=0.85

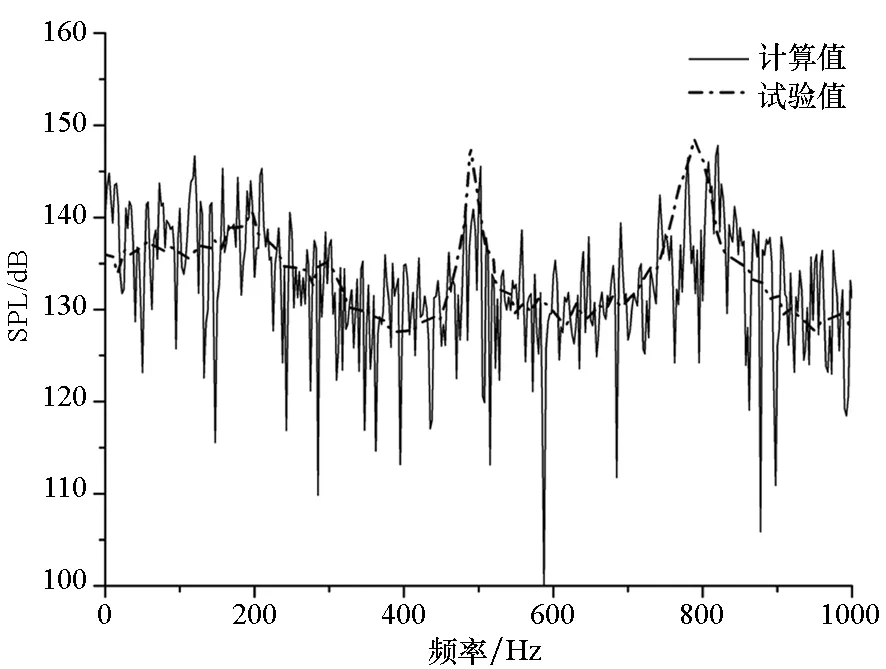
(a) K22(X/L=0.25)

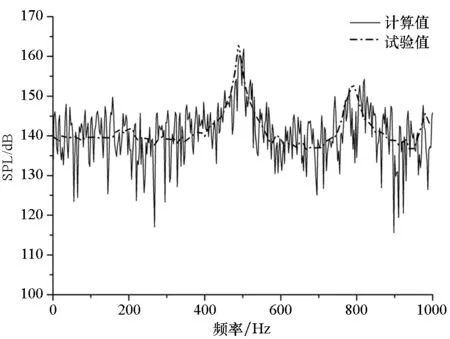
(b) K25(X/L=0.55)

(c) K29(X/L=0.95)图13 Ma=1.35监测点声压频谱特性计算与试验对比Fig.13 Comparison of spectrum between calculation and test at Ma=1.35

计算结果表明，不同马赫数下不同位置的模态一致，这与文献中给出的典型频谱符合很好。从频谱模态中可以看出，采用本方法进行气动噪声计算，前4阶频谱模态均可以被捕捉到，且除个别模态略有差别外，主频均被精确捕捉到，说明本方法具有较高精度。Ma=1.35时，噪声测点声压级分布集中在130～170dB之间，上游声压级略低，而下游声压级略高。对于类似结构的内埋弹舱而言，如此高的声压级会对舱体以及舱内武器造成疲劳损伤，且这种分布会使舱内武器生成一定的抬头力矩，这主要是由于上游剪切层与下游壁面边界层互相作用产生不稳定压力波，该不稳定压力波主要集中于下游区域，并且从下游沿壁面向上游传播至上游前缘，再与剪切层互相作用使之与壁面分离从而形成声学反馈。在空腔中主要的不稳定区域集中于下游，使得下游噪声声压级明显高于上游。

气动噪声计算中最重要是主频位置及其对应的最高声压级的预测，重点对这两个参数的仿真与试验结果进行了对比。表1为Ma=0.6，Ma=0.85，Ma=1.35下空腔底部前中后三个位置的数值仿真结果与试验结果中的最高声压级对比，表2为主频对比。

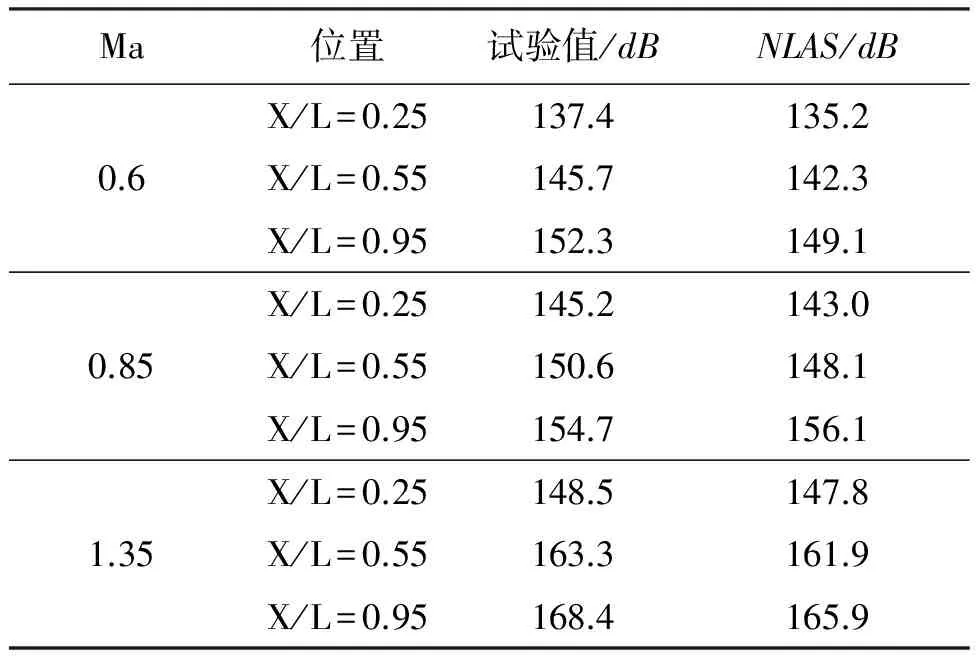
表1 最高声压级比较

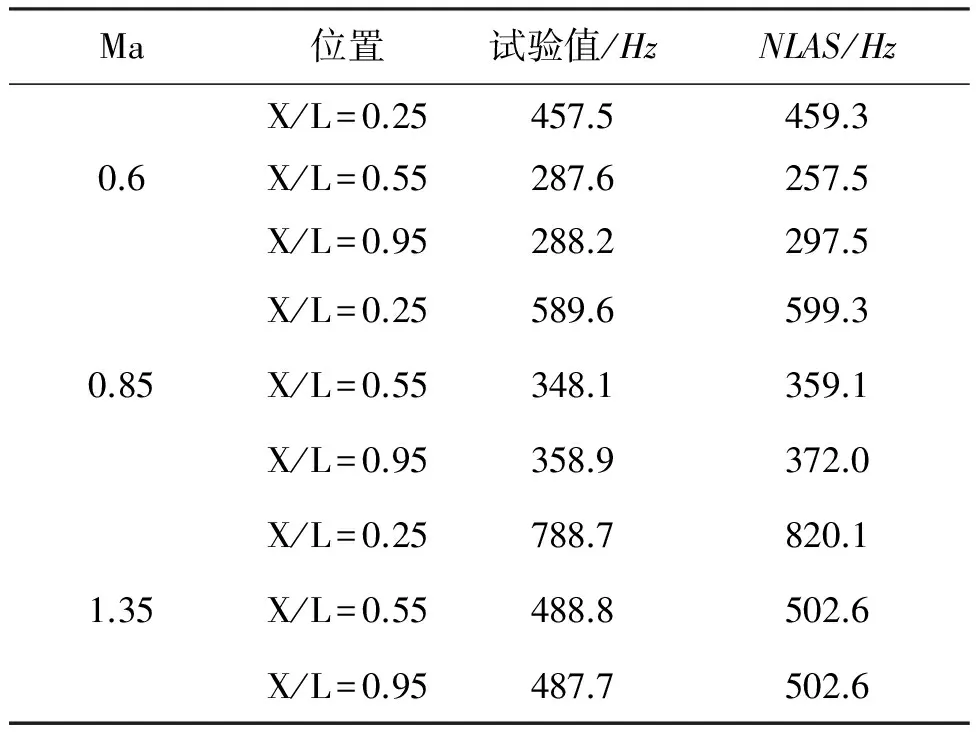
表2 主频位置比较

通过对比不同马赫数下NLAS仿真与试验的最高声压级以及主频位置，可以发现NLAS方法能较为精确地模拟出亚、跨、超声速情况下空腔噪声主频及其对应的最高声压级。

4 结论

1)将非线性噪声求解方法NLAS应用于空腔噪声预测，模拟了Ma=0.6，Ma=0.85，Ma=1.35三种来流条件下的空腔噪声。应用cubick-ε湍流模型，远场吸收边界及壁面函数法计算得到了三种来流条件下空腔噪声特性，数值结果与试验结果基本吻合，特别是准确模拟主频及其对应的最高声压级，表明NLAS方法在亚、跨、超声速条件下对空腔噪声有较好的预测能力。

2)非线性噪声求解方法对于近壁面网格要求低，声场计算域比RANS小，可减少噪声计算网格数量，降低计算成本。将NLAS计算结果与国外文献中DES计算结果进行对比，NLAS的计算精度与DES相当，但是网格数大大降低，因此NLAS方法对于内埋弹舱工程快速设计具有一定的意义。

3) 对于L/D=5的典型开式空腔，通过对亚、跨、超声速情况下空腔噪声数值计算与试验对比，随着马赫数的增大，各监测点的噪声主频位置，总声压级都有所增大。

References)

[1]MicharelJH. 战术导弹空气动力学[M].洪金森,杨其德，毛国良，译.北京：宇航出版社,1999.

MicharelJH.Tacticalmissileairdynamics[M].TranslatedbyHONGJinseng,YANGQide,MAOGuoliang.Beijing:AstronavigationPress, 1999. (inChinese)

[2]MurrayNE,UkeileyLS.Flowfielddynamicsinopencavityflows[C]//Proceedingsof12thAIAA/CEASAeroacousticsConference,AIAA2006-2428, 2006.

[3] 吴继飞，罗新福，范召林．内埋式弹舱流场特性及武器分离特性改进措施[J]．航空学报，2009，30(10)：1840-1845．WUJifei,LUOXinfu,FANZhaolin.Flowcontrolmethodtoimprovecavityflowandstoreseparationcharacteristics[J].ActaAeronauticaetAstronauticaSinica，2009，30(10)：1840-1845. (inChinese)

[4]LeTH,MaryI,TerracolM.LESofpressureloadssuppressioninweaponsbayflow[C]//Proceedingsof43rdAIAAAerospaceSciencesMeetingandExhibit,AIAA2005-794, 2005.

[5]AllenR,MendonçaF.DESvalidationsofcavityacousticsoverthesubsonictosupersonicrange[C]//Proceedingsof10thAIAA/CEASAeroacousticsConference,AIAA2004-2862, 2004.

[6]PengSH,HaaseW.AdvancesinhybridRANS-LESmodelling,notesonnumericalfluidmechanicsandmultidisciplinarydesign[M].USA:Springer, 2008 : 132-141.[7]BattenP，RibaldoneE,CasellaM,etal.Towardsageneralizednon-linearacousticssolver[C]//Proceedingsof10thAIAA/CEASAeroacousticsConference,AIAA2004-3001, 2004.

[8]BattenP，GoldbergU,ChakravarthyS.Reconstructedsub-gridmethodsforacousticspredictionsatallReynoldsnumbers[C]//Proceedingsof8thAIAA/CEASAeroacousticsConference&Exhibit,AIAA2002-2511, 2002.

[9]DaSilvaCRI,DeAlmeidaO,BattenP.Investigationofanaxi-symmetricsubsonicturbulentjetusingcomputationalaeroacousticstools[C]//Proceedingsof13thAIAA/CEASAeroacousticsConference,AIAA2007-3656, 2007.

[10]HenshawMJ.M219cavitycase:verificationandvalidationdataforcomputationalunsteadyaerodynamics[R].ResearchandTechnologyOrganization,RTO-TR-26,AC/323(AVT)TP/19, 2002.

Nonlinear numerical simulation of cavity noise

WANG Yiding1,CHEN Binqi1, GUO Liang2, ZHONG Fanjun2,TONG Mingbo1

InordertoevaluatetheM219cavitynoiseat0.6, 0.85and1.35Machnumber,nonlinearacousticsolveriscombinedwithReynolds-averagedNavier-Stokesequations.TheflowfieldofacavityiscalculatedbymeansofReynolds-averagedNavier-Stokesequations,whichcontainsbasiccharacteristicsofaverageflowfieldandturbulencestatisticalaveragesolutionofstatisticsdescriptionofturbulencefluctuation.Noisesourceisrefactoredbythenonlinearacousticsolver.Spreadofpressurefluctuationissimulatedprecisely.Acomparisonshowsthatthesimulationresultsofnonlinearacousticsolveragreewellwiththeexperimentresults.Comparedwithdetachededdysimulation，nonlinearacousticsolvercangreatlyreducetheamountofmesh.Inaddition,themethodcanprovidesomereferenceforinternalweaponsbaydesign.

cavity;nonlinearity;source;turbulence;internalweaponsbay

2014-02-10

王一丁(1985—)，男，四川乐山人，博士研究生，E-mail：wyding127@163.com；童明波(通信作者)，男，教授，博士，博士生导师，E-mail: tongw@nuaa.edu.cn

10.11887/j.cn.201504025

http://journal.nudt.edu.cn

V

A