L-矩阵多参数预条件AOR迭代法收敛性分析

罗 芳，康淑瑰，王振芳

（山西大同大学数学与计算机科学学院，山西大同，037009）

L-矩阵多参数预条件AOR迭代法收敛性分析

罗 芳，康淑瑰，王振芳

（山西大同大学数学与计算机科学学院，山西大同，037009）

文章主要研究了L-矩阵多参数预条件AOR迭代方法中参数的选取对收敛速度的影响，并给出了相应的比较定理,最后通过数值例子来进行说明。

预条件;AOR迭代法;L-矩阵;M-矩阵;收敛

考虑线性方程组

不失一般性，设A=I-L-U是一个n×n的非奇异矩阵,D是A的对角矩阵,-L和-U分别为A的严格下三角和上三角部分，x和b是n维列向量,迭代求解方程组(1)的AOR[1]方法定义为:

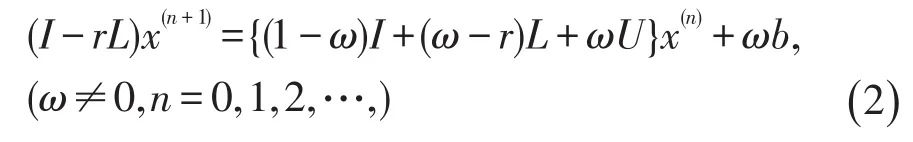
它的迭代矩阵表示为：

其中r和w≠0均为实参数，分别称为加速因子与超松弛因子。当r=0,w=1时，AOR方法为Jacobi方法；当r=1,w=1时，AOR方法为Gauss-Seidel方法；当w=r时，AOR方法即为SOR方法。

当r≠0时，AOR方法可以看作是SOR方法的外推，记作ESOR方法。此时，若记，则有：

1 解线性方程组的AOR方法

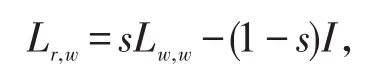
因此，若记μ为SOR方法的迭代矩阵Lw,w的特征值，λ为相应的Lr,w的特征值，则成立下面关系式：

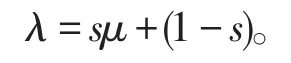
定理1[1]若A为L-矩阵，且满足 0≤r≤w≤1(w≠0)，则解方程组（1）的AOR方法收敛的充分必要条件是解方程组（1）的Jacobi方法收敛。

2 预备知识

为方便起见，我们首先给出一些将在后面用到的定义、引理和定理。

定义1[2]设A=[aij]∈Rm×n,如果aij≥0,对一切i,j成立,则称A是非负的,记为A≥0;如果aij＞0对一切i,j成立,则称A是正的,记为A＞0。如果A,B∈Rm×n满足A-B≥0,则记为A≥B；类似地，可以定义A＞B。通过n×1矩阵，也可以定义一个n维列向量x≥0,x＞0。

此外，我们用ρ(A)表示A的谱半径。

定义2[2]设A=[aij]∈Rn×n,若aij≤0,i≠j。则称A是Z-矩阵；称矩阵A=(aij)∈Rn×n为L-矩阵，若aii＞0,i=1,2,…,n,且aij≤0，i≠j。对于任一个Z-矩阵A,都可表示成A=sI-B,其中s是一个正数,B≥0。如果一个Z-矩阵A满足s≥ρ(B),则称A是M-矩阵。当s＞ρ(B)时,称之为非奇异的M-矩阵，其中ρ(A)表示A的谱半径。

引理1[3](Frobenius-Perron定理)若矩阵A≥0为不可约矩阵，则

(1)A存在一个正的实的特征值等于它的谱半径ρ(A)；

(2)相应于ρ(A)，存在一个正的特征向量x＞0，称为A的Perron向量；

(3)ρ(A)是矩阵A的一个单特征值;

(4)ρ(A)随矩阵A的任一元素增加而增加。

引 理 2[2]若A=[aij]∈Rn×n,A≥0,x=(ξj)∈Rn,x＞0。若α,β≥0使得αx≤Ax≤βx，则α≤ρ(A)≤β;若αx＜Ax,则ρ(A)＞α;若Ax＜βx，则ρ(A)＜β。特别地,若Ax=λx,则λ=ρ(A)。

引理3[2]A=[aij]∈Rn×n是一个Z-矩阵,则下列命题等价:

(1)A是非奇异的M-矩阵;

(2)A非奇异且A-1≥0;

(3)存在x∈Rn满足x＞0使得Ax＞0。

定义3[3]矩阵A称为单调的,如果Ax≥0，则必有x≥0。

定义4[4]如果M是非奇异的,则称A=M-N为矩阵A的分裂;如果ρ(M-1N)＜1,则称分裂收敛;如果M是非奇异的M-矩阵且N≥0则称为M-分裂;如果M-1≥0且N≥0,则称为正则分裂;如果M-1≥0且M-1N≥0,则称为弱正则分裂。

引理4[4]设A=M-N是一个M-分裂,则ρ(M-1N)＜1，当且仅当A是非奇异的M-矩阵。

引理5[5]若A,B都是非奇异的M-矩阵,如果A≤B,则A-1≥B-1。

引理6[6]关于A的一个正则分裂A=M-N,ρ(M-1N)＜1，当且仅当A是一个单调矩阵。

引理7[7]设A1=M1-N1,A2=M2-N2分别是单调矩阵A1,A2的弱正则分裂,使得如果存在一个正向量x使得0≤A1x≤A2x,且，则关于x的单调范数有

“谁在外面？”病房里的人听见门口的动静出声询问。雷染君回过神，抹干眼泪站起来，看见姜祈缓缓下了床，艰难地挪动到门边。雷染君推开门，目光第一时间落在他病服袖口之外的缠着纱布的双腕上。她紧紧抿住嘴唇，双手局促不安地握在一起。头发束成的马尾也像失去了往常的活力，毫无生气地耷拉着。

特别是如果当M-11N1存在一个正的Perron向量，则有

进一步，若x是的正的Perron向量，且（4）不等式严格成立，则（5）不等式也严格成立。

3 主要结论

为改善求解线性方程组(1)的迭代法的收敛速度或者使原来不收敛的迭代法变得收敛，往往对线性方程组进行预条件处理。其基本思想是在方程组的两端同时左乘一个特殊的可逆矩阵P∈Rn×n(P称为预条件因子)，左乘方程组(1)后，使原方程组变为

关于AOR方法的预处理是在2001年由D J Evans等人提出的，取预条件因子P=I+S，到目前为止，已经有许多种取S的方法,证明在多参数预条件因子Pα=I+Sα下AOR方法的收敛性。

其中：

0≤αij≤1(1≤i≠j≤n)是参数,其相应的预条件系统的AOR方法的迭代矩阵记为：

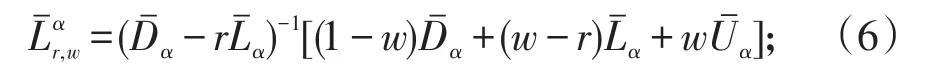
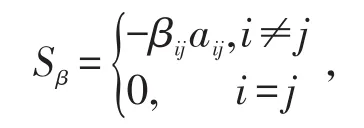
0≤βij≤1(1≤i≠j≤n)，其相应的预条件系统的AOR迭代矩阵为：

为了讨论的方便，我们先取

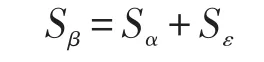
其中，

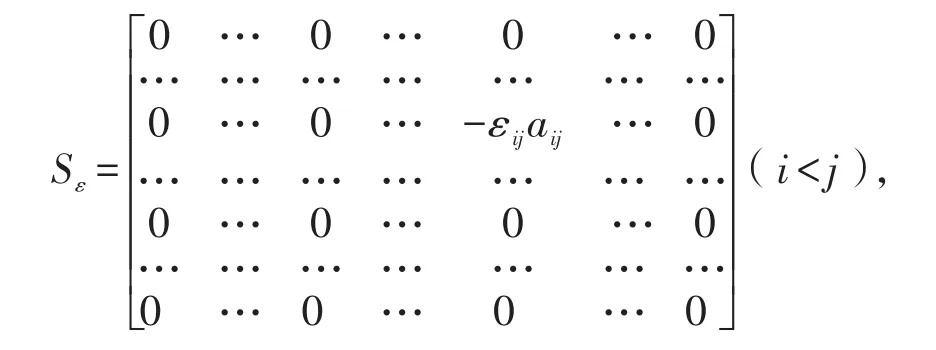
则，

而

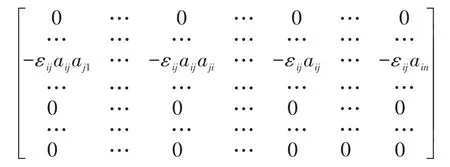
因此，若A是一个L-矩阵，则有故有，又均为M-矩阵，故由引理5，必有。又由文献[4]的定理2知，均为非负不可约矩阵，故由引理1，Lˉαr,w有正的Perron向量，再结合引理7，有

进一步，我们取Sε的上三角部分均为参数形式，即

可以得到，（8）式仍然成立。

对于Sε若为下三角的情形，我们同样先来考虑其简单形式，即取

则此时

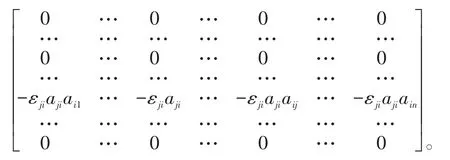
同理，当Sε的下三角部分均为参数形式时（9）亦成立。

综上讨论，我们可以得到：

定理2设A是一个L-矩阵,,其中:，满足：,则若ρ(Lr,w)＜1，0≤r≤w≤1,w≠0,就有＜1，且随着αij的增大，谱半径变小，进而，当αij均取为1时，谱半径最小。即当

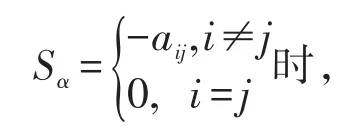
对应的预条件AOR方法收敛最快。

4 数值例子

为了说明含参预条件因子中参数对AOR方法收敛性的影响，我们考虑以下算例，见表1。设A为(其中由αij(i＞j)全部取为0.2,αij(i＜j)全部取为0.3所得；由αij(i＞j)全部取为0.4,αij(i＜j)全部取为0.5所得；由αij(i＞j)全部取为0.6,αij(i＜j)全部取为0.5所得；由αij(i≠j)全部取为1所得。

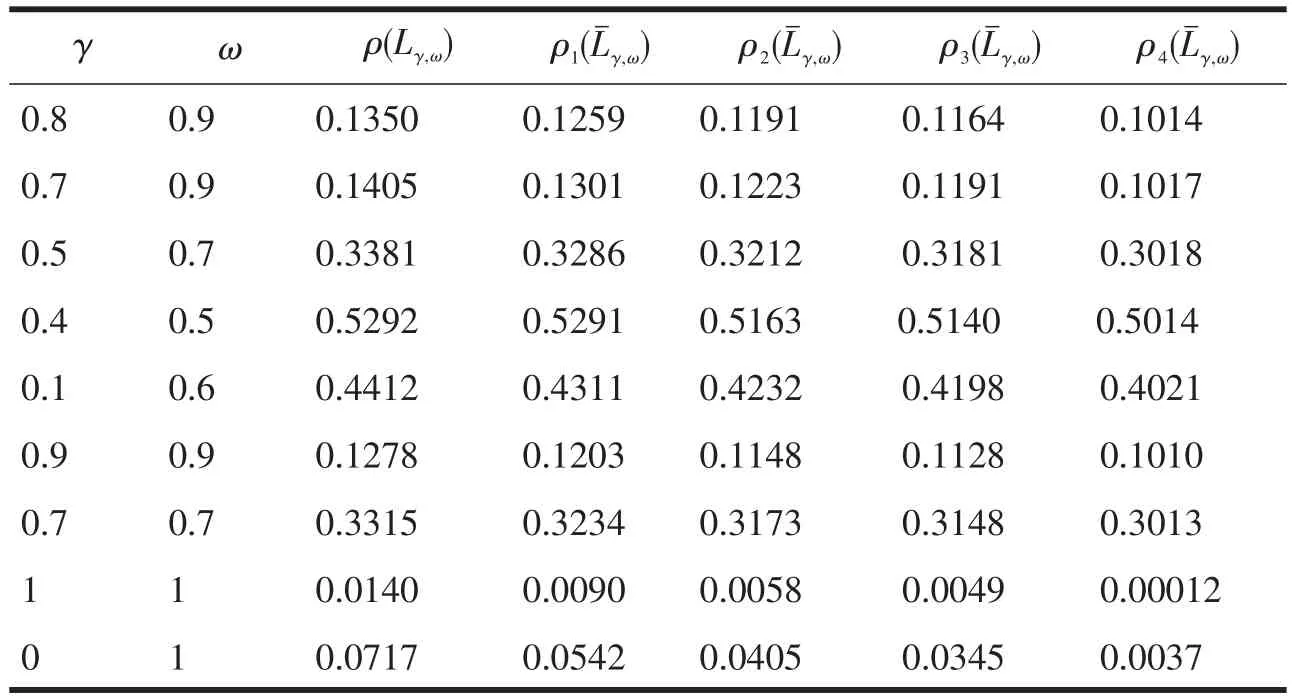
表1 选取不同的预条件因子下AOR迭代法的谱半径比较

[1]HADJIMOS A.Accelerated overrelaxation method[J].Math Comp,1978（32）:149-157.

[2]徐树方.控制论中的矩阵计算[M].北京:高等教育出版社，2011:37-44.

[3]YOUNG D M.Iterative Solution of Large Linear Systems[M].New York：Academic Press,1971.

[4]LI Wang.Comparison Results for AOR Iterative Method with a New Preconditioner[J].Internatonal Journal or Nonlinear Science,2006,2(1):16-28.

[5]CAO Z H.On the convergence of nested stationary iterative methods[J].Linear Algebra and its Applications,1995(221):159-170.

[6]VARGA R S.Matrix Iterative Analysis[M].New Jersey:Prentice-Hall,1981.

[7]NEUMANN M,PLEMMONS R J.Convergence of parallel multi-splitting iter-ative methods for M-matrices[J].Linear Algebra Appl,1987(88∕89):559-573.

〔责任编辑 高海〕

The Convergence Analysis of Multi-parameters Preconditioned AOR Iterative Method for L-matrices

LUO Fang,KANG Shu-gui,WANG Zhen-fang
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

The paper mainly studied the parameter’s influence on the rate of convergence for L-matrix multi-parameter preconditioned AOR iterative method A At the same time the corresponding comparison theorem is given.Lastly,we provide numerical experiments to illustrate the theoretical results.

preconditioner;AOR iterative method;L-matrix;M-matrix;convergence

O241.6

A

1674-0874(2015)06-0003-04

2015-09-15

山西大同大学校级科研资助项目[2012K7]

罗芳(1970-),女,山西右玉人,硕士，副教授,研究方向：计算数学。