多准则下反导作战单、多遭遇点预测模型*

李龙跃，刘付显，杨国哲，王东旭，王 菊

(空军工程大学 防空反导学院， 陕西 西安 710051)

多准则下反导作战单、多遭遇点预测模型*

http://journal.nudt.edu.cn

李龙跃，刘付显，杨国哲，王东旭，王 菊

(空军工程大学 防空反导学院， 陕西 西安 710051)

整个反导射击过程可以简单看作一个基于预测的遭遇点起始的，不断重复、修正的过程。分析遭遇点预测的时间和空间前提，并给出遭遇点预测的3个基本准则；在多准则下建立了单遭遇点预测模型，给出了模型公式中未知量的转化方法；分射击-观察-射击和射击-射击两种情况建立了多准则下多遭遇点预测和优化模型，并给出了拦截弹最晚发射时间的计算方法；就观察时机对遭遇点预测的影响进行了分析与建模。部分研究属于探索性的研究，相关结论对指控模型开发和实施连续反导，从方法和作战理念方面提供了一些参考。

反导作战；单遭遇点；多遭遇点；观察时机；预测模型

(AirandMissileDefenseCollege,AirForceEngineeringUniversity,Xi′an710051,China)

防空作战中，预判或评估杀伤目标的一个重要办法就是概率判断法，而当前和未来大多反导武器发射的拦截弹进入到与目标弹头的交战空域时，通过弹上综合制导雷达上传的信息进行目标捕获和跟踪，最终释放拦截器依靠动能直接撞击杀伤目标，属于典型的直接碰撞杀伤(HitToKill，HTK)。一些文献围绕反导遭遇点预测相关问题进行了前期研究，荆武兴等[1]考虑了不同发射场景下，如何通过快速规划拦截弹飞行方案和发射时间窗口来提高反导拦截弹的反应能力，重点研究反导遭遇时间的计算方法；王君等[2]研究了地空导弹(非机动)空气动力目标过程中遭遇点的预测问题；张友安等[3]在论文中提到了舰空导弹一般情况下弹目遭遇点的计算方法；万雨君等[4]建立了基于“当前”统计情况的遭遇点预测模型，而其重点是给出对机动目标的拦截弹导引律。国外方面，美国、以色列研制和部署的反导系统最为先进，相关研究也有很多成果，主要集中于反导拦截器的导航与制导控制等方面[5-8]。

除了上述研究，对于反导遭遇点预测还有一些问题需要关注：一是要判断火力单元从空间和时间上是否适宜对目标进行拦截；二是要考虑不同的预测准则，如果反导武器的射击准则不同，那么遭遇点的预测结果也就不同；三是面对同一波次多个目标攻击，除了单遭遇点计算，还要考虑计算多个遭遇点和拦截弹的发射时间间隔等问题。李龙跃等从以上三个问题出发，分析遭遇点预测的空间-时间前提，建立多准则下的单个、多个遭遇点预测模型，并就一些模型细节进行了探讨。

1 遭遇点预测的前提和预测准则

1.1 遭遇点预测的空间-时间前提

拦截飞机目标时通常要求目标对火力单元的航路捷径小于火力单元的最大杀伤航路捷径，且目标高度处在火力单元的杀伤高度范围内，飞机在不做大角度机动时，满足上述两点情况下一般都通过火力单元杀伤区[9]。同样，当弹道导弹目标飞经火力单元水平杀伤范围时，此时目标高度和目标相对火力单元的斜距分别处于该火力单元导弹拦截高度、导弹拦截斜距范围内时，目标才有机会被拦截。因此，目标弹道与火力单元杀伤区必须要有交点，用T表示目标、Rmax，Rmin分别表示火力单元最大和最小拦截斜距、Hmax,Hmin分别表示最大和最小拦截高度，则空间拦截可行性条件为Rmax≤RT≤Rmin，Hmax≤HT≤Hmin。

这里把目标离开杀伤区时刻与到达杀伤区时刻间的时间段称为杀伤时间窗口，当目标在时刻t(介于到达杀伤区时刻和离开杀伤区时刻之间)，拦截器飞至预测遭遇点，则满足拦截可行性时间条件。杀伤时间窗口可根据目标当前时刻，位置，速度以及火力单元位置，拦截弹杀伤最大、最小拦截斜距，最大、最小拦截高度迭代计算得到。理论上，只要目标在某时刻t尚未穿越火力单元杀伤区近界都可能是遭遇点，图1是遭遇点可预测性判断流程图。

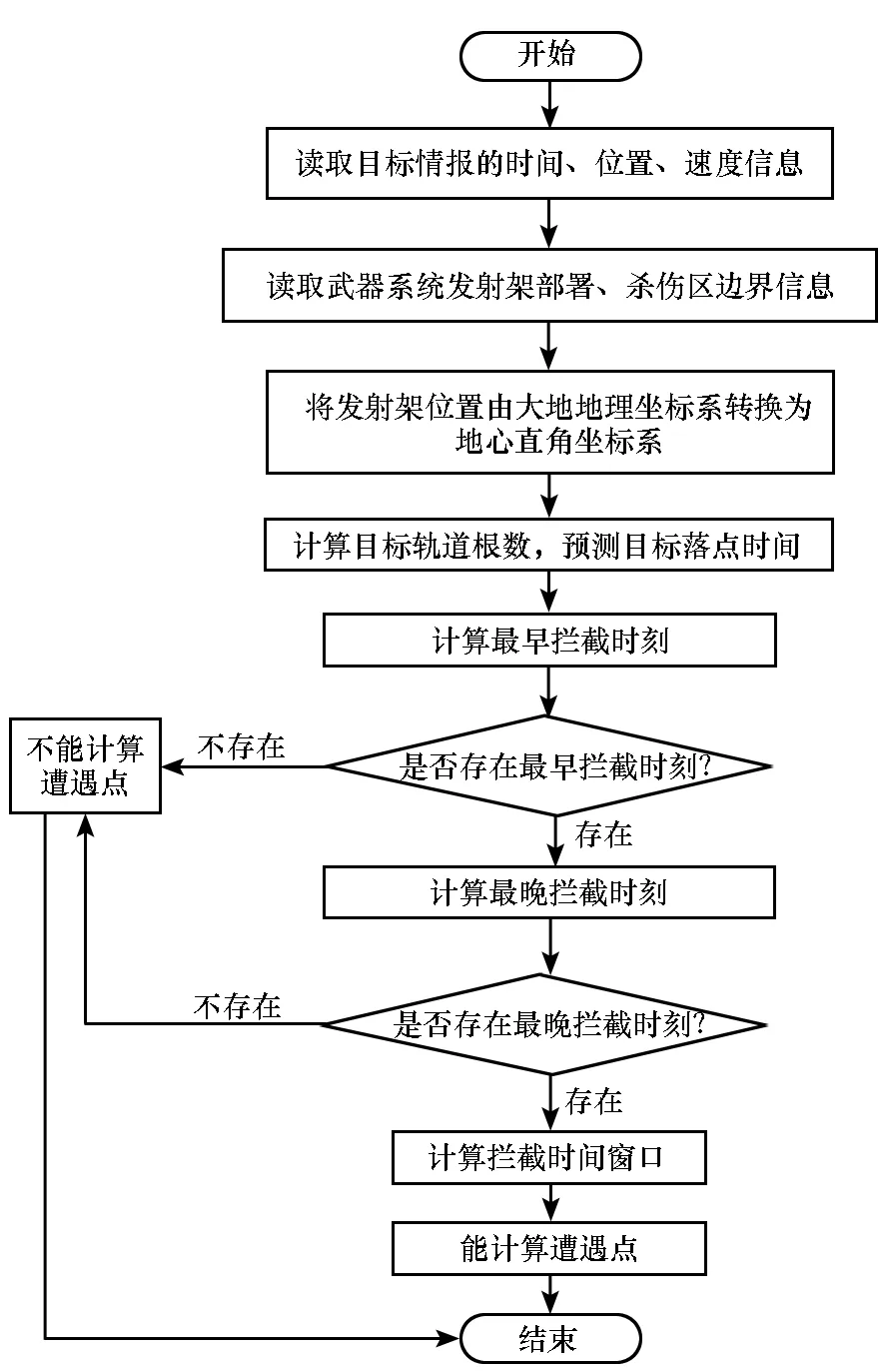
图1 遭遇点可预测性判断流程图Fig.1 Forecastability estimating process of impact point

1.2 遭遇点预测准则

根据反导射击习惯，将遭遇点预测准则分为：尽远准则、尽近准则和最大概率拦截准则。1)尽远准则。对弹道导弹目标一般情况下要尽量实现尽早发现、尽远拦截，尽远准则是为了充分利用拦截时间，尽可能多地增加拦截次数，提高总的拦截概率[10]。2)尽近准则。为了先拦截更重要的目标，有时把相对次要的目标尽可能排在最后面拦截，满足在杀伤区内构成一次射击条件即可。3)最大概率拦截准则。武器系统雷达对目标探测跟踪的时间越长，对目标的轨道参数预测越准确，计算出的遭遇点误差也越小。最大概率拦截准则要求遭遇点处于拦截器对目标的最佳杀伤点处，此时拦截概率最大。图2是3种准则下的遭遇点空间位置示意图。

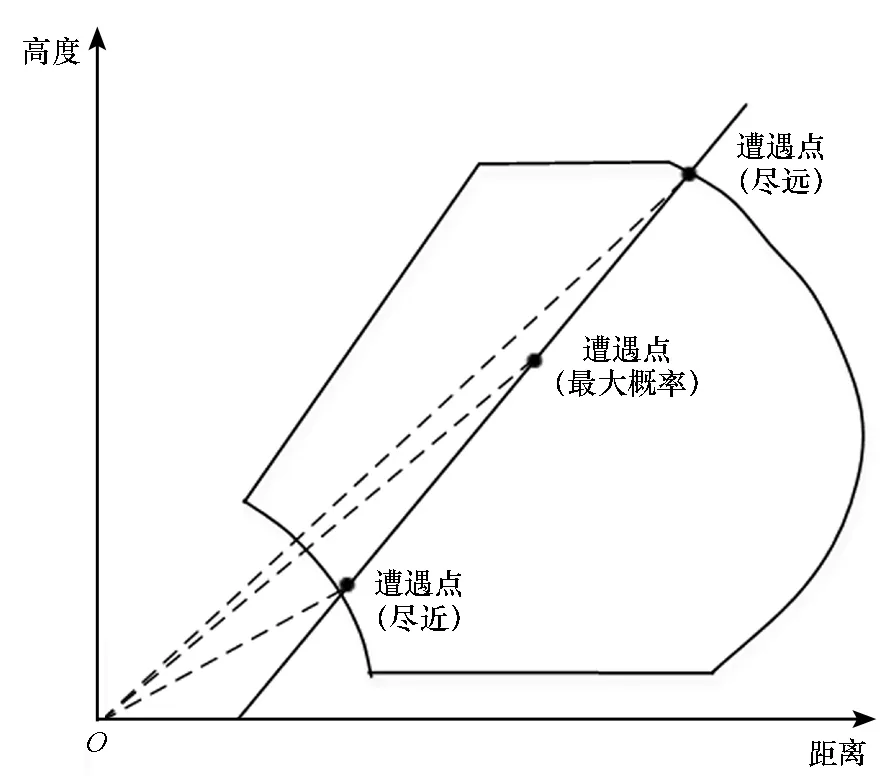
图2 不同准则下的遭遇点空间位置示意图Fig.2 Schematic of impact points at different criterions

2 多准则下单遭遇点预测模型

表1是本文所用参数及说明。

2.1 基本计算公式

单遭遇点拦截，是对来袭目标只进行一次拦截，一般情况下是由拦截需求和拦截边界条件限制决定的，一般适用于两种情况：一是只需要一次拦截就能满足拦截目标的需要；二是由于边界条件的限制，仅够完成一次拦截所需要的资源或时间。过程中可能出现两种情况：1)同时到达的多个目标[11-12]，研究相对成熟；2)目标到达具有一定时间间隔，研究相对较少。以尽远准则为例，尽远准则下遭遇点即为目标杀伤区远界与目标弹道的交点位置。根据相对运动原理，目标飞到最远遭遇点的时间与拦截弹从发射点到达遭遇点的时间相等，即

tpq(hit)-tpjy(launch)q=tpq(hit)-tqL

(1)

(2)

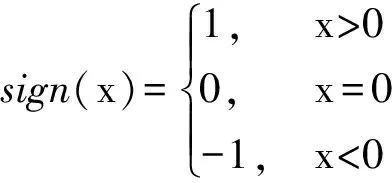
(3)

由式(2)可计算出尽远准则下单遭遇点的坐标

(4)

尽近准则、最大概率拦截准则与尽远准则下的单遭遇点计算一样，变量取不同值即可得到相应的不同准则下的公式，可用统一的式(5)来计算。

(5)

2.2 基本计算公式中未知量的转化

2.1节中的计算公式中并非所有未知量都是实际可获取的，仍以尽远准则下单遭遇点预测为例，假设目标位置L点相对于发射架pi的测量值为(Spi,φpi,εpi)，则

(6)

现在已经对式(4)中第一项完成了转化，α,β,LI分别可由式(7)～(9)计算得到。

(7)

(8)

(9)

由式(1)、式(2)可得

其中

(11)

(12)

先将式(9)代入式(7)、式(8)，式(11)、式(12)代入式(10)，最后再将式(8)、式(10)、式(7)代入式(4)可得未知量的转化后的尽远准则下单遭遇点计算模型。tpq1计算方法见3.1节，至此尽远准则下单遭遇点预测模型仅需输入目标L相对于发射架pi的测量值、目标落点坐标和发射架pi的坐标就可计算出遭遇点坐标，最大概率拦截准则和尽近准则下单遭遇点预测方法与上述方法一致。

3 射击-观察-射击模式下多准则多遭遇点预测模型

3.1 尽远准则下多遭遇点预测模型

(13)

式(13)中除了tpq1，其他参数均为已知。可看出式(13)是个以tpq1为变量的一元二次方程，依据一元二次方程求根公式

(14)

其中a,b,c分别对应的是式(13)中的二次项系数，一次项系数和常数项，则tpq1为

(15)

显然式(15)有2个解，取tpq1值较小的解，同样方法可求tpqi，将其代入式(12)，可以计算出尽远准则下第i个发射架发射的拦截弹第i次拦截目标时的遭遇点坐标(i为非0正整数)。

(16)

3.2 尽近准则下最晚发射时间点计算模型

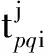
(17)

尽近准则下最晚发射时间点对应的弹头位置本质上是尽近遭遇点的上一个遭遇点，则

(18)

(19)

(20)

3.3 最大概率拦截准则下遭遇点预测模型

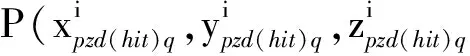
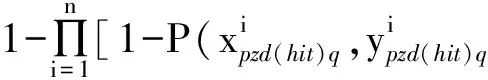
(21)

与尽远准则下遭遇点计算思路非常类似，式(22)是预测遭遇点Li的坐标计算公式，注意到如果将式(22)方形框中项变为Δt，则式(22)变为点L′的坐标计算公式，如果将式(22)方形框中项变为(Δt+tpq1)，则式(22)变为点L1的坐标计算公式。

(22)

将式(22)代入到式(21)中，便可进行相关模型求解工作。

4 射击-射击模式下多准则多遭遇点预测模型

4.1 尽远准则下多遭遇点预测模型

在射击-射击模式下需要考虑拦截弹发射时间间隔的确定问题，发射时间间隔分固定、可变两种。设发射时间间隔为Δtpq(launch)，(Δtpq(launch))min为最小发射间隔，设分配给目标的拦截弹数量为Q，其余参数沿用表1中给定参数，则

(Δtpq(launch))min≤Δtpq(launch)≤(Δtpq(launch))max

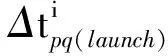
(Δtpq(launch))min

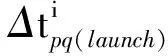
(23)

(24)

4.2 最大拦截概率准则下多遭遇点预测模型

射击-射击模式下最大概率拦截准则时多遭遇点优化模型可将式(21)进行改写，分固定发射间隔和可变发射间隔两种情况。

固定发射间隔可由式(25)求得。

利用软件中的灵敏度分析功能对理论塔数进行分析。初始条件为，原料进料位置：第5块，萃取剂进料位置：第3块，回流比：1，溶剂比：0.9，对塔板数进行灵敏度分析。

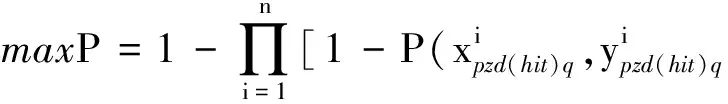
(25)

可变发射间隔可由式(26)求得。

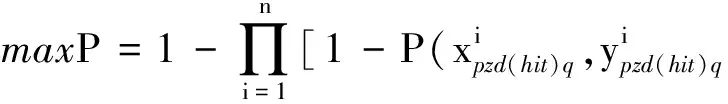
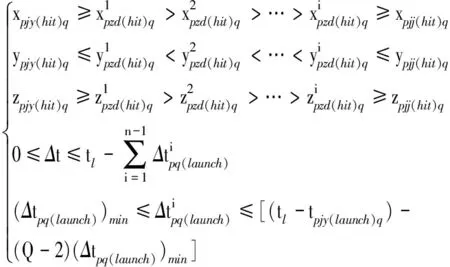
(26)

式(25)、式(26)中的遭遇点计算公式为

(27)

(28)

(29)

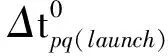
(30)

据此可对式(29)做进一步化简。

5 观察时机对遭遇点预测影响分析

由于存在杀伤效果观察环节，射击-观察-射击模式要比射击-射击模式更节省拦截弹资源，除了以上两种模式外，还有典型如“射击-射击-观察-射击-射击”“射击-射击-观察-射击”“射击-观察-射击-射击”等混合模式，实际作战也可以从“射击-射击-观察-射击”“射击-观察-射击-射击”中择优选取。观察时机的选取对遭遇点预测影响很大，尽远准则下的遭遇点预测需要尽远、尽快完成对目标的拦截过程。

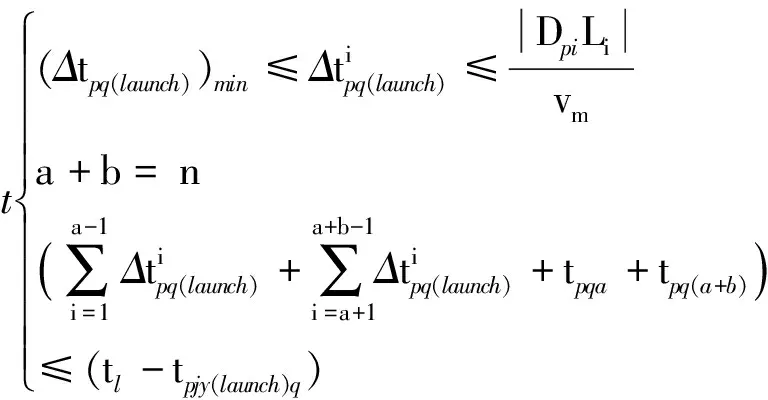
(31)

(32)

(33)

(34)

(35)

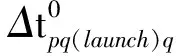
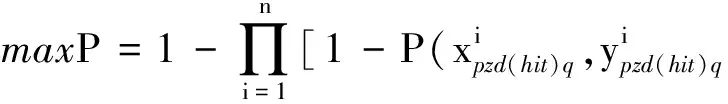
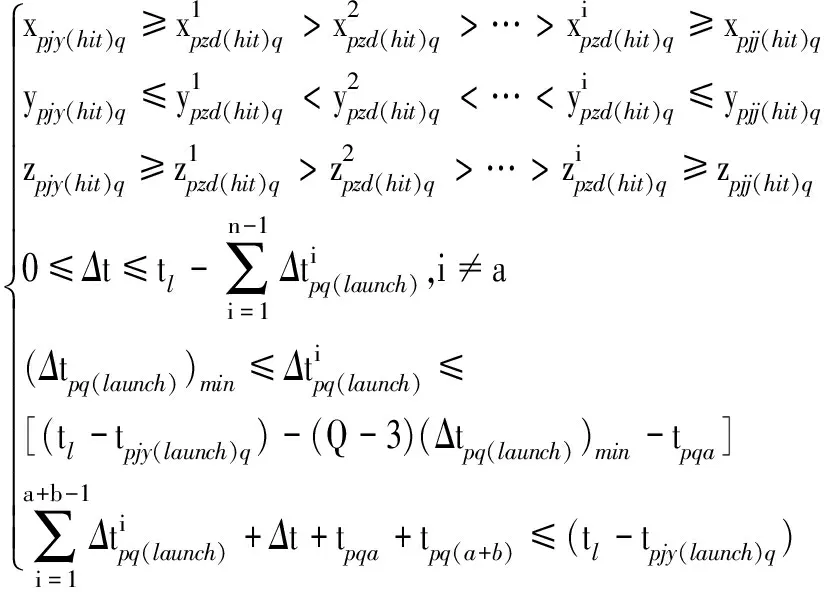
(36)

6 实例分析

假设有2枚来袭弹道导弹，见表2，已知2个目标的弹道与武器杀伤区远、近界的交点[14]，设杀伤区边缘的杀伤概率为0.6。

显然，根据表2不同准则下的单遭遇点坐标可以直接得到。假设目标1只能有一个遭遇点，对目标2分别采取射击-观察-射击和射击-射击两种模式，对目标3采取射击-射击-观察-射击模式，则尽远准则下3个目标的遭遇点坐标和杀伤概率见表3。

限于篇幅，不再算出其他准则下3个目标的遭遇点坐标和杀伤概率。根据目标2的参数，代入射击-观察-射击模式下的最大概率拦截遭遇点计算模型，可得滞后发射时间Δt与杀伤概率之间的关系图，如图3所示。在拦截目标2的过程中，Δt不能大于30s，否则不能保证两次拦截，两个遭遇点的总杀伤概率在Δt=30s时取得最大值，不再写出具体结果。对目标2，代入射击-射击模式下的最大概率拦截遭遇点计算模型，这里取发射间隔为10s和20s，经过仿真得到滞后发射时间与每个遭遇点及总杀伤概率之间的关系，见图4和图5。

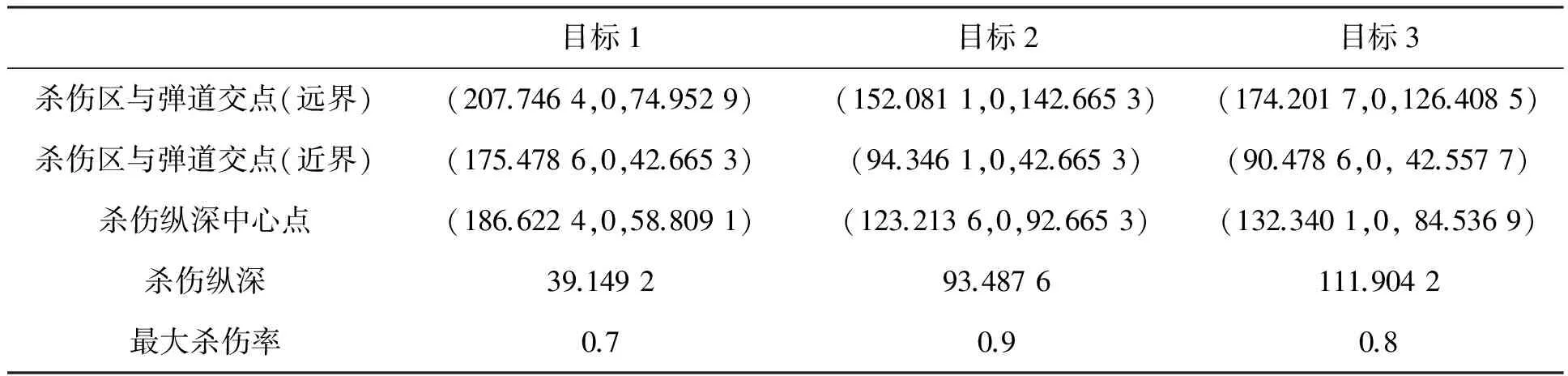
表2 相关已知参数[14]

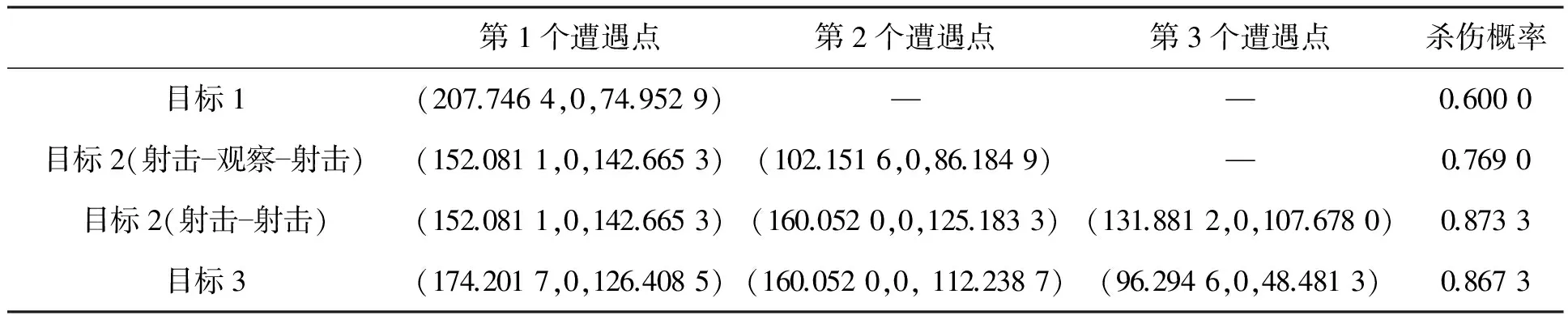
表3 尽远准则下3个目标的遭遇点坐标和杀伤概率

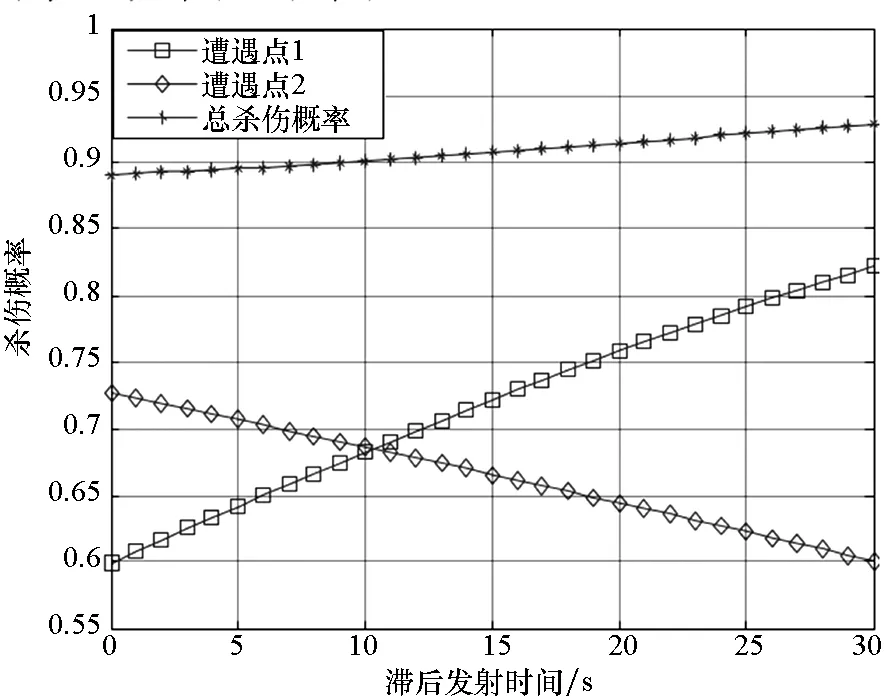
图3 对目标2在射击-观察-射击模式下滞后发射时间与杀伤概率关系图Fig.3 Relationship between interceptors′ delayed launch time and kill probabilities at shoot-look-shoot mode of shooting target 2

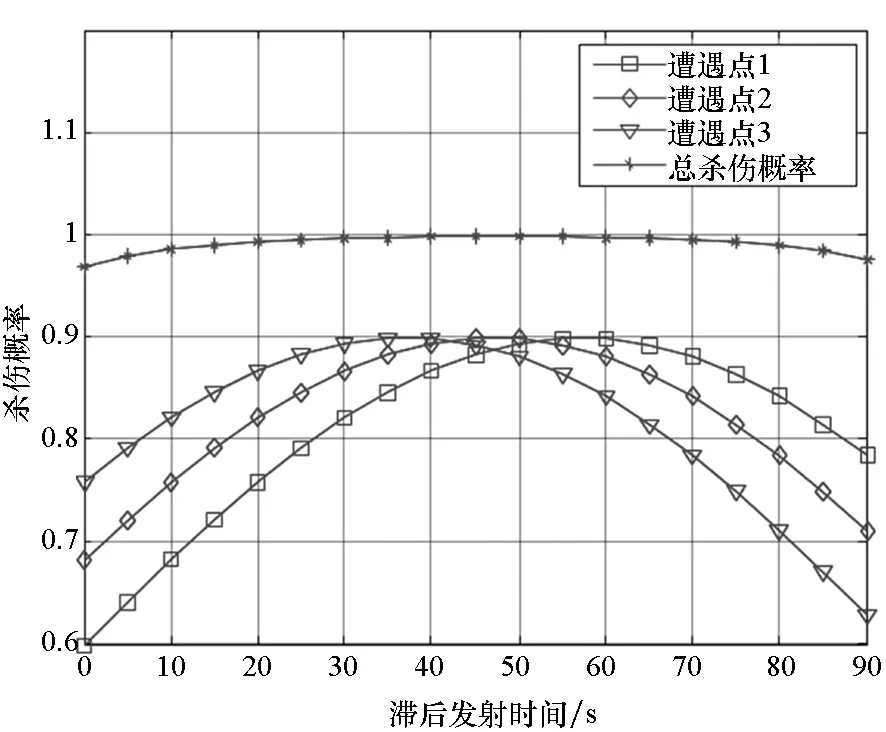
图4 对目标2在射击-射击模式下滞后发射时间与杀伤概率关系图(发射间隔为10s)Fig.4 Relationship between interceptors′ delayed launch time and kill probabilities at shoot-shoot mode of shooting target 2 (shot interval is 10s)

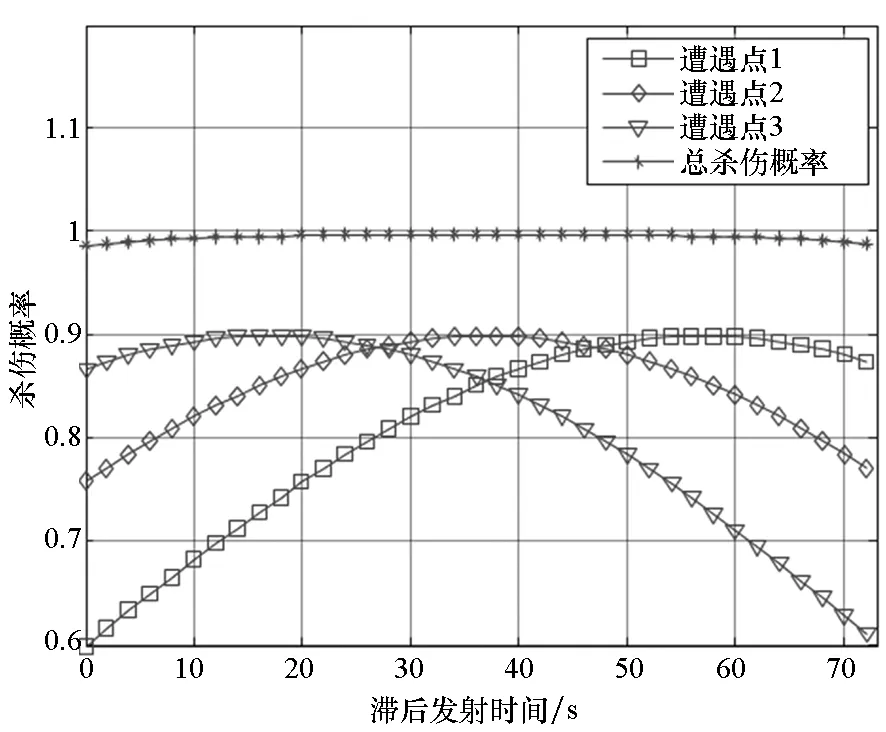
图5 对目标2在射击-射击模式下滞后发射时间与杀伤概率关系图(发射间隔为20s)Fig.5 Relationship between interceptors′ delayed launch time and kill probabilities at shoot-shoot mode of shooting target 2 (shot interval is 20s)

图4和图5可以看出目标2在发射-发射模式下，发射间隔为10s时，最佳滞后发射时间为45s；发射间隔为20s时，最佳滞后发射时间为36s

(前提是不小于武器系统最小发射间隔)。本文模型除了算出遭遇点坐标外，还可以计算出最佳滞后发射时间，见表4。

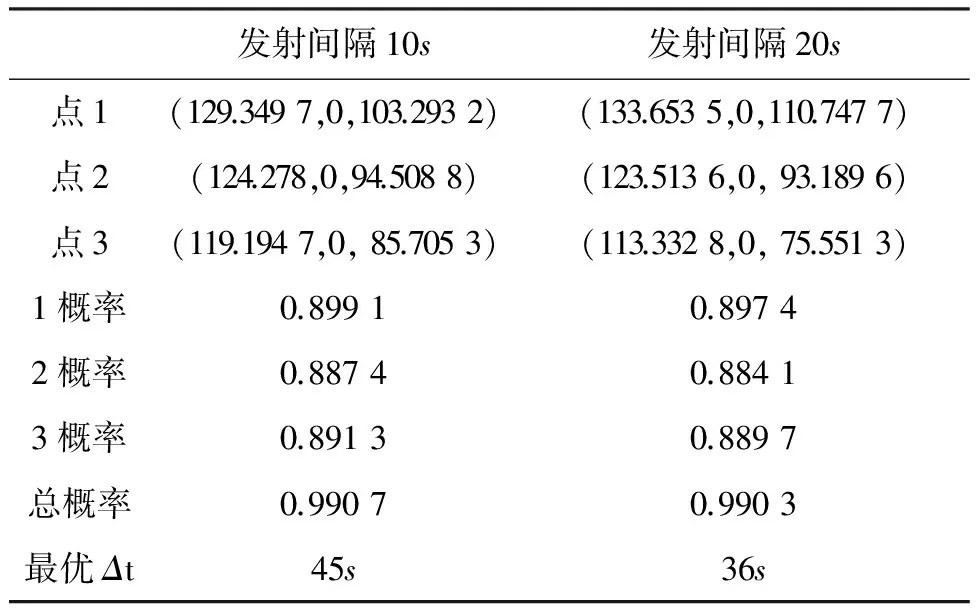
表4 对目标2在不同发射间隔下的遭遇点预测结果

限于篇幅，对目标3的遭遇点参数计算不再写出。通过实例分析，验证了模型的可用性，此外，还可以看出最大概率拦截准则下对目标的杀伤概率的确有所提高，射击-射击模式比射击-观察-射击模式的杀伤概率高，其原因在于发射间隔选取比较灵活。

7 结论

遭遇点预测本质上是一个计算过程，此外，目标指示信息的精度和弹道预测的准确度对准确预测遭遇点至关重要。主要在多准则下建立了反导作战单个核多个遭遇点预测模型，部分方法具有一定探索性，下一步还要考虑拦截弹的导引规律去确定发射点到遭遇点之间拦截弹的轨迹，而不是假设成直飞逼近。此外，计算方程的变量较多，求解问题得进一步研究。

References)

[1] 荆武兴,李罗钢,高长生.反导拦截飞行方案及时间窗口快速搜索算法[J].系统工程与电子技术,2013,35(6):1256-1261.

JINGWuxing,LILuogang,GAOChangsheng.Fastsearchalgorithmofflightprogramandlaunchtimewindowforinterceptionanti-missile[J].SystemsEngineeringandElectronic, 2013, 35(6):1256-1261.(inChinese)

[2] 王君,周林,雷虎民. 地空导弹与空中目标遭遇点预测模型和算法[J].系统仿真学报,2009,21(1):80-83.WANGJun,ZHOULin,LEIHumin.Forecastmodelandarithmeticonhitpointofground-to-airmissileandaerialtarget[J].JournalofSystemSimulation, 2009, 21(1):80-83. (inChinese)

[3] 张友安,马国欣,万宇. 一种弹目遭遇点预测方法[J]. 海军航空工程学院学报,2011,26(5):513-516.

ZHANGYouan,MAGuoxin,WANYu．Amethodtopredictimpactpointofmissileandtarget[J].JournalofNavalAeronauticalEngineeringInstitute, 2011, 26(5):513-516.(inChinese)

[4] 万雨君,刘鲁华,陈克俊,等. 基于预测命中点的机动目标最优制导方法[J]. 国防科技大学学报,2012,34(5):21-25.

WANYujun,LIULuhua,CHENKejun,etal．Optimalguidancelawbasedonhitpointforecastformaneuveringtarget[J].JournalofNationalUniversityofDefenseTechnology, 2012, 34(5):21-25.(inChinese)

[5]DwivediPN,BhalePG,BhattacharyyaA,etal．Generalizedstateestimationandmodelpredictiveguidanceforspiralingandballistictargets[J].JournalofGuidance,Control,andDynamics, 2014, 37(1):243-264.

[6]LiuYF,QiNM,TangZW.Effectsofdivert-thrustersonhomingperformanceofendo-atmosphericinterceptors[J].JournalofOptimizationTheoryandApplications, 2013, 156(2):345-364.

[7]ZhengLL.BallisticmissileinterceptionfromUCAV[D].USA：NavalPostgraduateSchool，2011.

[8]KuiZL,FangYF,ChuanTX.Researchoncompoundcontroltechniquewithlateralimpulsivethrustvectorforairdefencemissile[C]. 32ndChineseControlConference(CCC2013), 2013, 10: 4386-4390.

[9] 全杰. 反导指挥决策的拦截可行性建模[J].指挥控制与仿真,2013,35(5):22-26.

QUANJie.Interceptingfeasibilitymodedofantimissilecommandingdecision[J].CommandControl&Simulation, 2013, 35(5):22-26.(inChinese)

[10] 季军亮,陈杰生,刘飞.匈牙利法的末段两层火力反TBM目标分配优化[J].火力与指挥控制,2011,36(10):192-195.

JIJunliang,CHENJiesheng,LIUFei.Optimizationoftargetsassignmentofdual-layerfireATBMinreentryphasebasedonhungary[J].FireControlandCommandControl, 2011, 36(10): 192-195. (inChinese)

[11] 符小卫,李金亮,高晓光. 防空威胁联网建模与分析[J].兵工学报,2013,34(7):904-909.

FUXiaowei,LIJinliang,GAOXiaoguang.Modelingandanalysingofair-defensethreatnetting[J].ActaArmamentarii, 2013, 34(7):904-909. (inChinese)

[12] 徐豫新,王树山,马晓飞.Monte-Carlo法在武器系统射击参量设计中的应用[J]. 系统工程理论与实践,2012, 32(4): 854-859.

XUYuxin,WANGShushan,MAXiaofei.ApplicationofMonte-Carlomethodonthedesignofammunitionsystemfiringparameters[J].SystemsEngineering-Theory&Practice, 2012, 32(4):854-859.(inChinese)

[13] 陈红彬,钱林方. 中口径火炮提前发射修正弹反导能力研究[J]. 弹道学报,2012,24(4):47-50.

CHENHongbin,QIANLinfang.Researchonleadinglaunchingtrajectorycorrectionprojectileofmediumcalibergunagainstmissile[J].JournalofBallistics, 2012, 24(4):47-50. (inChinese)

[14] 段锁力. 末段高层反导火力单元任务规划关键问题研究[D].西安：空军工程大学，2012.

DUANSuoli.Researchonthepivotalmissionplanningproblemsoftheterminalhighaltitudeanti-missileweapon[D].Xi′an:AirForceEngineeringUniversity, 2012. (inChinese)

Multi-criteria forecast models of antimissile single/multiple impact points

LI Longyue, LIU Fuxian, YANG Guozhe, WANG Dongxu, WANG Ju

Thewholeantimissileprocesscanbeviewedasaniterativelyprocessbasedonimpactpointsforecastingwhichshowesthatimpactpointswasmainlyfocusedonbypresentresearchinthefollowingway.Thetime-spacerequirementsforimpactpointsforecastingwereanalyzed,and3forecastingcriterionswereproposed.Theantimissilesingleimpactpointsforecastingmodelat3criterionswasestablished,andtheunknownvariablesofthemodelwerechangedintovalueswhichradarcanmeasure.Forshoot-look-shootscenarioandshoot-shootscenario,antimissilemultipleimpactpointsforecastingandoptimizationmodelwasgaveat3criterions,andthecalculatingmethodoflatestlaunchtimewasdiscussed.Theimpactofdifferentlookoccasionwasanalyzedandmodeledduringimpactpointsforecastingprocess.Partialtheoriesandmethodswasexploratoryresearch,relatedconclusionsmademaybebenefitsforantimissilesustainedshootingdecisionmaking.

antimissilebattle;singleimpactpoint;multipleimpactpoints;lookoccasion;forecastmodel

2014-10-24

全军军事学研究生资助项目(2014JY525)

李龙跃(1988—)，男，河南驻马店人，博士研究生，E-mail：lilong_yue@126.com； 刘付显(通信作者)，男，教授，博士，博士生导师，E-mail：liuxqh@126.com

10.11887/j.cn.201504029

TJO

A