数形结合思想在二次函数中的应用

高春侠

“数（代数）”与“形（几何）”是数学的两个基本研究对象，这两个内容既互相独立又互相联系，体现在数学解题过程中包括“以数解读形”和“以形分析数”两个方面。数形结合思想就是把数和形有机组合，使数学问题得到转化，“形”让“数”更具体明了，“数”使“形”更形象灵活。因此，数形结合思想在数学解题中有广泛的应用。数形结合思想在二次函数中的应用比较广泛，借助数形结合思想可以方便快捷地解决二次函数问题，怎样利用数形结合思想解决二次函数问题呢？要在解题中有效实现“数形结合”，最好能够明确“数”与“形”常见的结合点，从“以数助形”角度来看，主要有以下两个结合点：第一，以数轴、坐标系为桥梁把函数图象几何化;第二，利用面积、距离、角度等几何量来解决二次函数问题。

一、在已知图形中搜集信息

二次函数图象的顶点在原点O，经过点A（1，1）;点F（0，1）在y轴上，直线y=﹣1与y轴交于点H。

（1）求二次函数的解析式;

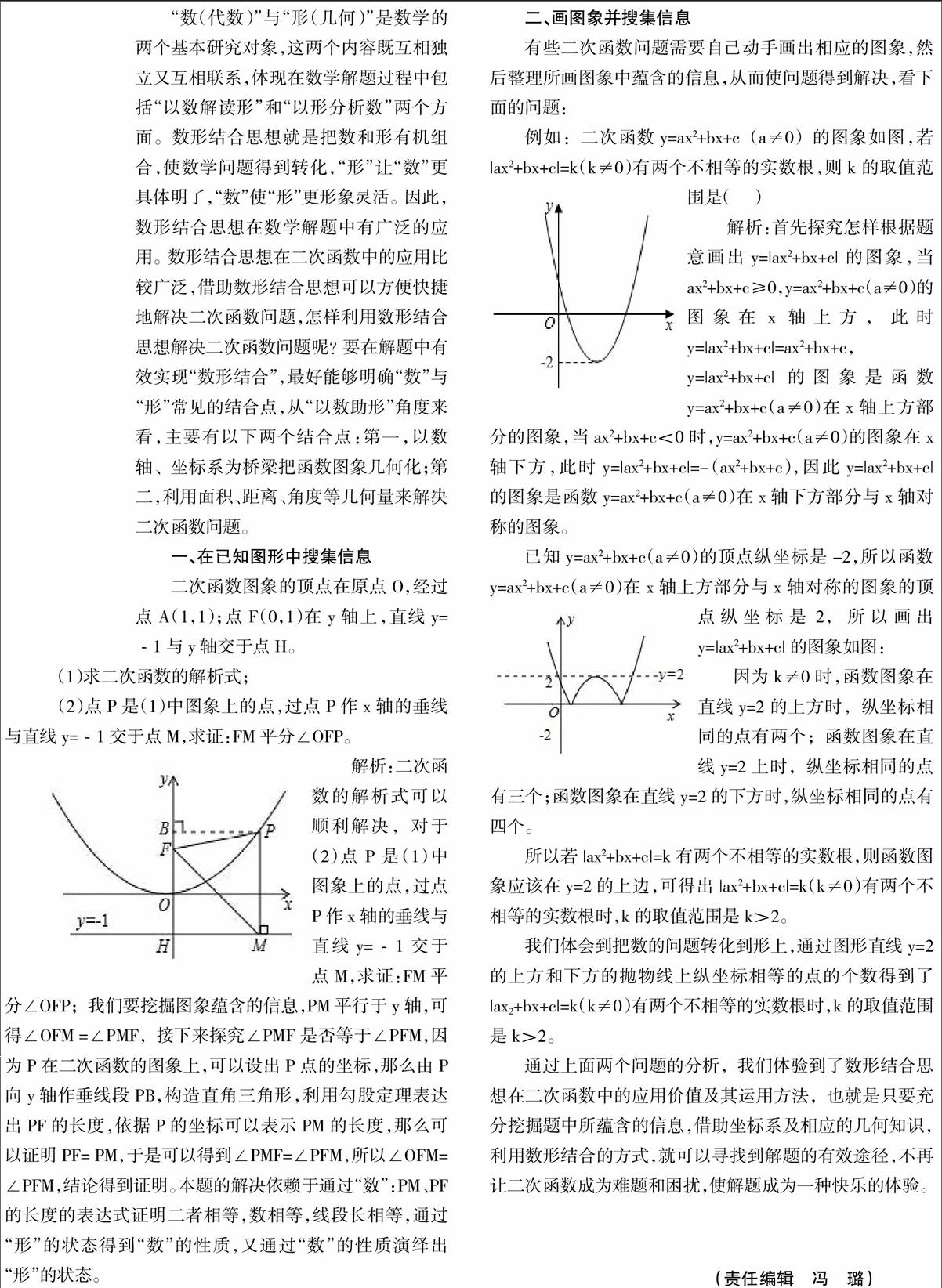
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP。

解析：二次函数的解析式可以顺利解决，对于（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP;我们要挖掘图象蕴含的信息，PM平行于y轴，可得∠OFM =∠PMF，接下来探究∠PMF是否等于∠PFM，因为P在二次函数的图象上，可以设出P点的坐标，那么由P向y轴作垂线段PB，构造直角三角形，利用勾股定理表达出PF的长度，依据P的坐标可以表示PM的长度，那么可以证明PF= PM，于是可以得到∠PMF=∠PFM，所以∠OFM=∠PFM，结论得到证明。本题的解决依赖于通过“数”：PM、PF的长度的表达式证明二者相等，数相等，线段长相等，通过“形”的状态得到“数”的性质，又通过“数”的性质演绎出“形”的状态。

二、画图象并搜集信息

有些二次函数问题需要自己动手画出相应的图象，然后整理所画图象中蕴含的信息，从而使问题得到解决，看下面的问题：

例如：二次函数y=ax2+bx+c（a≠0）的图象如图，若|ax2+bx+c|=k（k≠0）有两个不相等的实数根，则k的取值范围是（ ）

解析：首先探究怎样根据题意画出y=|ax2+bx+c|的图象，当ax2+bx+c≥0，y=ax2+bx+c（a≠0）的图象在x轴上方，此时y=|ax2+bx+c|=ax2+bx+c，y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象，当ax2+bx+c<0时，y=ax2+bx+c（a≠0）的图象在x轴下方，此时y=|ax2+bx+c|=-（ax2+bx+c），因此y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴下方部分与x轴对称的图象。

已知y=ax2+bx+c（a≠0）的顶点纵坐标是-2，所以函数y=ax2+bx+c（a≠0）在x轴上方部分与x轴对称的图象的顶点纵坐标是2，所以画出y=|ax2+bx+c|的图象如图：

因为k≠0时，函数图象在直线y=2的上方时，纵坐标相同的点有两个;函数图象在直线y=2上时，纵坐标相同的点有三个;函数图象在直线y=2的下方时，纵坐标相同的点有四个。

所以若|ax2+bx+c|=k有两个不相等的实数根，则函数图象应该在y=2的上边，可得出|ax2+bx+c|=k（k≠0）有两个不相等的实数根时，k的取值范围是 k>2。

我们体会到把数的问题转化到形上，通过图形直线y=2的上方和下方的抛物线上纵坐标相等的点的个数得到了|ax2+bx+c|=k（k≠0）有两个不相等的实数根时，k的取值范围是k>2。

通过上面两个问题的分析，我们体验到了数形结合思想在二次函数中的应用价值及其运用方法，也就是只要充分挖掘题中所蕴含的信息，借助坐标系及相应的几何知识，利用数形结合的方式，就可以寻找到解题的有效途径，不再让二次函数成为难题和困扰，使解题成为一种快乐的体验。

（责任编辑 冯 璐）