双隶属度模糊粗糙支持向量机

韩虎，党建武

兰州交通大学电子与信息工程学院，兰州730070

双隶属度模糊粗糙支持向量机

韩虎，党建武

兰州交通大学电子与信息工程学院，兰州730070

针对支持向量机方法处理不确定信息系统时存在的两个问题：一方面支持向量机训练对噪声样本敏感，另一方面支持向量机训练未考虑信息系统的不一致，利用模糊理论与粗糙集方法分别计算得到两种隶属度：模糊隶属度与粗糙隶属度，并将两种隶属度引入到标准支持向量机中得到一个新的支持向量机模型——双隶属度模糊粗糙支持向量机（DM-FRSVM）。分析该模型对于不确定问题的解决思路并进行对比研究，实验结果表明，在对于含有不确定信息的样本集进行分类时，DM-FRSVM表现出更好的推广性能。

支持向量机；不确定问题；模糊理论；粗糙集

1　引言

支持向量机方法在很多应用中取得了很好的推广性能，但是对于不确定信息的处理，标准支持向量机方法还存在着许多困难。然而在实际应用系统中，信息的不完全、不精确或模糊性又时常发生，因此对于不确定条件下的支持向量机研究就显得尤为重要［1-3］。

知识获取的不确定性主要来源于两个方面：一是数据本身的不确定性，二是信息系统中知识有限的分辨能力引起的不确定性［4-5］。对于数据本身的不确定性（主要包括噪声或孤立野值点）往往通过模糊技术予以解决，由知识有限的分辨能力引起的不确定性问题，粗糙集提供了丰富的理论与方法［6-7］。

针对以上两种不确定性问题，有学者通过引入模糊理论与粗糙集方法，分别得到两种不确定支持向量机模型：模糊支持向量机（FSVM）与粗糙支持向量机（FRSVM）［8-9］。模糊支持向量机是根据不同输入样本对分类的贡献不同赋以不同的隶属度，从而消弱噪声或野点对分类的影响。粗糙支持向量机利用模糊粗糙集中的下近似算子为每个训练样本分配隶属度，解决了条件属性与决策类标之间的不一致性问题，通过放松约束条件，使求出的最优超平面间隔变大，从而提高支持向量机的泛化能力。模糊支持向量机与模糊粗糙支持向量机都是针对不确定问题提出的两种求解模型，它们的不同点主要体现在下面三个方面：

（1）FSVM使用每个训练样例隶属于该样例的类标所在集合的隶属度对C-SVM原始问题目标函数中该样例的错分程度进行惩罚，重新规划了软间隔支持向量机。FRSVM利用模糊粗糙集中的下近似算子为每个训练样例分配一个隶属度，在硬间隔SVM的约束条件中通过每个样例的隶属度适当地放松约束条件，重新规划了硬间隔支持向量机。

（2）FSVM中隶属度的计算考虑的总是样本与样本所在类之间的关系，距离类中心越近，则样本获得的隶属度值也就越大。但是FRSVM中隶属度的计算考虑的却是与其最近的异类样本之间的关系，距离最近的异类样本越远，则隶属于下近似的程度越大，即隶属度值越大。

（3）FSVM的主要目的是消弱噪声或野点对分类的影响，而FRSVM的目的是解决条件属性与决策类标之间的不一致性问题，两种不确定方法的侧重点不同。

然而在一个实际的信息系统中，往往同时包含了上述两种不确定信息，本文提出一种新的双隶属度模糊粗糙支持向量机模型（DM-FRSVM），该模型同时利用模糊理论与粗糙集方法，分别为每个训练样本计算得到两种不同性质的隶属度，将得到的两种隶属度融入到标准支持向量机模型中，得到一个新的优化问题。

2　标准支持向量机

对于给定的一组样本集｛xi，yi｝，i=1，2，…，l，这里yi=1或-1，SVM依据结构风险最小化原则，将其学习过程转化为如下所示的优化问题；

其中训练样本xi被函数zi=φ（xi）映射到高维特征空间，w∈RN是超平面的系数向量，b∈R为阈值，ξi为松弛变量，C≥0是一个常数，控制对错分样本惩罚的程度。

采用拉格朗日乘子法把上述优化问题转换为其对偶问题：

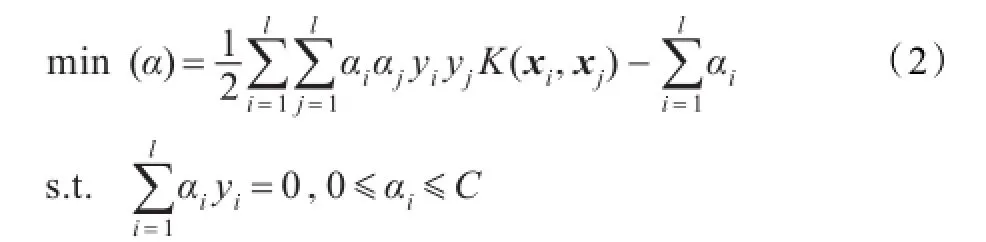
于是相应的分类决策函数为：

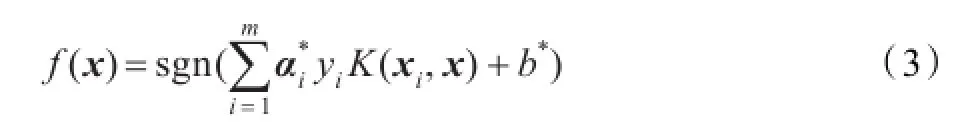
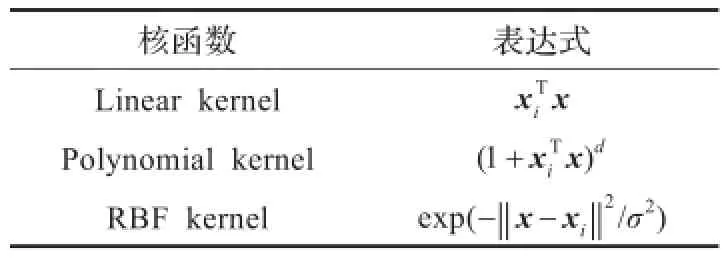
表1　常用核函数

3　双隶属度模糊粗糙支持向量机（DM-FRSVM）

模糊支持向量机通过对噪声或异常样本指定较小的隶属度，从而抑制噪声对分类器的影响；模糊粗糙支持向量机利用模糊粗糙集中的下近似算子为每个训练样例分配一个隶属度，用于解决条件属性与决策属性之间的不一致性问题。然而在一个实际的信息系统中，往往同时包含了上述两种不确定信息，本文同时利用模糊理论与粗糙集方法，分别为每个训练样本计算得到两种不同性质的隶属度，将得到的两种隶属度融入到标准支持向量机模型中，构造了一种新的双隶属模糊粗糙支持向量机模型。

3.1两种隶属度计算方法

为了方便描述，给两种隶属度分别命名为粗糙隶属度和模糊隶属度。

（1）粗糙隶属度

定义1给定非空有限论域U，R是U上的二元模糊关系。如果对于任意∀x，y，z∈U，R满足以下性质

①自反性：R（x，x）=1；

②对称性；R（x，y）=R（y，x）；

③传递性：min（R（x，y），R（y，z））≤R（x，z），称R是一个模糊等价关系。

更一般的，如果对∀x，y，z∈U，R满足自反性和对称性，同时满足T-传递性；T（R（x，y），R（y，z））≤R（x，z），则称R是模糊T-等价关系。

定义2给定非空有限论域U，如果实值函数k:U×U→R满足半正定性和对称性，那么该函数被称为核函数。例如高斯函数：

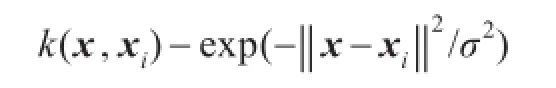
定理1［11-12］任意值域在单元区间的核函数k:U×U→［0，1］，且满足k（x，x）=1，那么k至少是Tcos（a，b）传递的，其中

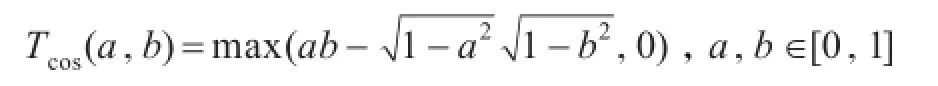
根据以上内容可知，部分核函数满足自反性、对称性和Tcos-传递性，那么由此类核函数计算的样本之间的关系是一个模糊Tcos-等价关系，核函数可用于模糊粗糙计算中的关系提取。因此将模糊粗糙集中的模糊关系用核函数代替，就得到了核模糊粗糙集模型，具体定义如下：

定义3［13］给定非空有限论域U和U上满足自反、对称和Tcos-传递的核函数k，对任意U上的模糊子集X∈F（U）的模糊下近似和上近似定义为：

以高斯核函数构造的模糊等价关系为基础，利用高斯核模糊粗糙集中的下近似算子为每个训练样本分配隶属度。对于如果x∈di，在计算时，需要搜索di以外的距离x最近的样本y，然后计算为x隶属于di类的模糊下近似的隶属度。换句话说，样本x隶属于其自身类别的下近似程度取决于其最近的异类样本，距离越大，则隶属于下近似的程度越大，当样本x∉di时，由于在di以外距离x最近的样本是其自身，因此。

（2）模糊隶属度

自2002年Lin提出模糊支持向量机以来，模糊支持向量机的研究主要集中在隶属度函数的设计方面。然而到目前为止，隶属度函数的设计还没有一个可遵循的一般性准则［14-15］。本文采用基于距离的模糊隶属度计算方法来确定模糊隶属度值。首先定义两类样本的中心，分别记为x+和x_，同时定义两类样本的半径：

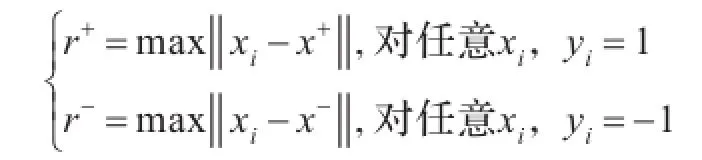
其中，‖‖·表示两点之间的欧氏距离，根据上面的定义构造隶属度函数如下：

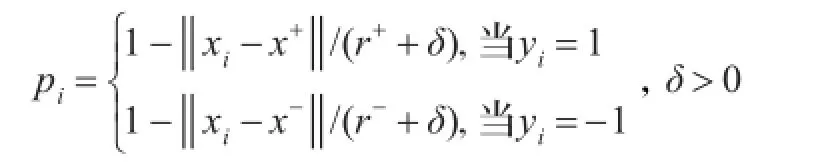
3.2DM-FRSVM

给定一组训练样本集（x1，y1），（x2，y2），…，（xl，yl）∈RN×Y，Y=｛-1，1｝，对于不确定问题，根据上面内容可以为每个样本分别计算得到模糊隶属度ui和粗糙隶属度si，将ui和si作为权重重新构造一组训练样本集（x1，u1，y1s1），（x1，u2，y2s2），…，（xl，ul，ylsl），其中yi代表样本所属的类别信息，即yi=1或yi=-1。为了描述简单，将上面加权训练样本集重新表示为：（x1，u1，y1），（x2，u2，y2），…，（xl，ul.yl）∈RN×Y，Y=［-1，1］，对于上述不确定问题的分类，构造双隶属度模糊粗糙支持向量机模型如下所示：

式（4）中约束项由模糊支持向量机中1-ξi变成了，因为在不确定分类问题中，样本已经由确切的属于某一类变成了以一定概率或一定隶属度属于某一类。采用拉格朗日乘子法求解优化问题（4），则得到式（5）的对偶优化问题：

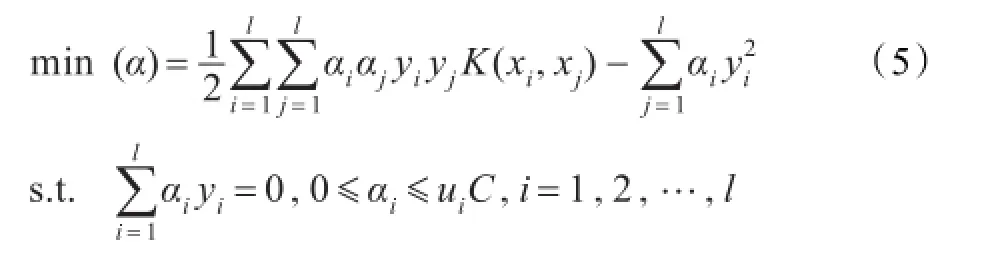
如果训练样本xi确切地属于某一类，即yi∈｛1，-1｝，那么上面所讨论的优化问题都与模糊支持向量机一致，再进一步，如果训练样本xi的模糊隶属度都为1，则上面所讨论的优化问题变成了标准支持向量机的形式。因此DM-FRSVM可以看做是对标准支持向量机和模糊支持向量机的进一步扩展。

4　实验结果与分析

本部分对UCI机器学习数据库中的5个基准数据集进行对比试验，它们的有关信息如表2所示。对于Iris数据集，将第1类与第3类合并为新的一类，第2类保持不变，对于Thyroid和Wine两个数据集，将第2类与第3类合并为新的一类，第1类保持不变，这样就将一个多类问题转化成了一个2分类问题。

表2　数据集信息

实验中对每个分类问题将数据标度到区间［0，1］，所有实验均采用RBF核函数，并给定其参数σ=1，同时给定拉格朗日乘子的上界C=100。实验分别采用标准支持向量机（SVM）、模糊支持向量机（FSVM）、模糊粗糙支持向量机（FRSVM）和双隶属度模糊粗糙支持向量机（DM-FRSVM）进行分类对比，表中测试误差都是在10重交叉验证基础上取平均值，具体内容见表3。

表3　对比实验结果

通过表3的实验数据可以看出，在上述5个基准数据库上，双隶属度模糊粗糙支持向量机的测试误差要低于其他三种支持向量机，分类性能明显要好于标准支持向量机。而模糊支持向量机与模糊粗糙支持向量机的结果并不一致，相比于标准支持向量机，在Iris数据集上模糊粗糙支持向量机的测试误差降低了2.96%，模糊支持向量机的测试误差提高了1.9%，在Wine数据集上，情况正好相反，模糊支持向量机的测试误差降低了0.29%，模糊粗糙支持向量机的测试误差提高了0.59%。

为进一步证实上面得出的两点结论，在上述5个数据集上选取10%靠近最优分类面的样本改变其类别属性。使用上面四种支持向量机进行对比研究，表中测试误差都是在10重交叉验证基础上取平均值，具体内容见表4。

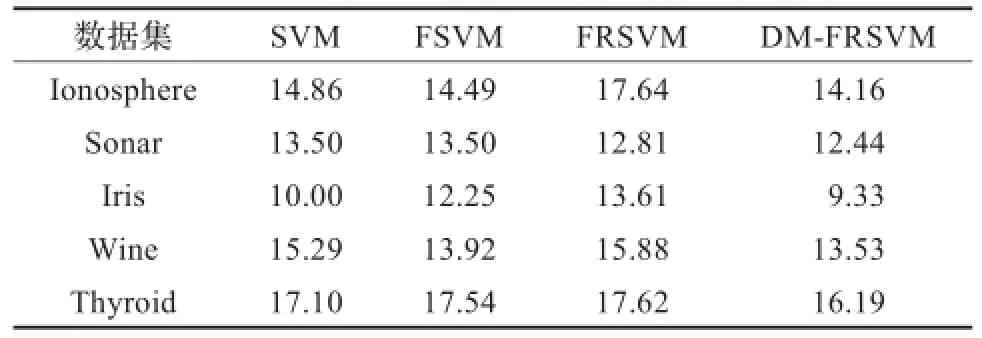
表4　对比实验结果

5　结论

本文针对支持向量机方法处理不确定信息系统时存在的两个问题：一方面支持向量机训练对噪声样本敏感，另一方面支持向量机训练未考虑信息系统的不一致性，利用模糊理论与粗糙集方法计算得到两种隶属度：模糊隶属度与粗糙隶属度，并引入到标准支持向量机中得到一个新的双隶属度模糊粗糙支持向量机模型（DM-FRSVM）。实验结果表明，在对于含有不确定信息的样本集进行分类时，DM-FRSVM表现出更好的推广性能。最终实验结果证实该方法在提高支持向量机效率，改善支持向量机结构方面是可行的。由于在该方法中涉及了多个参数的选取，因此进一步研究各参数地选取和分析它们之间的关系是需要进一步研究的问题。

［1］邓乃杨，田英杰.数据挖掘中的新方法—支持向量机［M］.北京：科学出版社，2005.

［2］Burgers C.A tutorial on support vector machines for patter recognition［J］.Data Mining and Knowledge Discovery，1998，2（2）：121-167.

［3］Sanchez V D.Advanced support vector machines and kernel methods［J］.Neuro Computing，2003：5-20.

［4］王国胤.Rough集理论在不完备信息系统中的扩充［J］.计算机研究与发展，2002，39（10）：1238-1243.

［5］Lin T Y.Granular computing-structures，representations，and applications［J］.Lecture Notes in Computer Science，2003，2639：16-24.

［6］Qian Y H，Liang J Y，Dang C.Consistency measure，inclusion degree and fuzzy measure in decision tables［J］.Fuzzy Sets and Systems，2008，159（18）：2353-2377.

［7］Lin C F，Wang S D.Training algorithms for fuzzy support vector machines with noisy data［J］.Pattern Recognition Letters，2004，25（14）：1647-1656.

［8］Chen Degang，He Qiang，Wang Xizhao.FRSVMs：Fuzzy rough set based support vector machine［J］.Fuzzy Sets and Systems，2010，161（4）：596-607.

［9］Lin C F，Wang S D.Fuzzy Support Vector Machines［J］. IEEE Trans on Neural Networks，2002，13（2）：464-471.

［10］刘华富.支持向量机Mercer核的若干性质［J］.北京联合大学学报，2005，19（1）：40-42.

［11］Yeung D S，Chen D G，Tsang E C C，et al.On the generalization of fuzzy rough sets［J］.IEEE Transactions on Fuzzy Systems，2005，13（3）：343-361.

［12］Moser B.On representing and generating kernels by fuzzy equivalencerelations［J］.JournalofMachineLearning Research，2006，7（12）：2603-2620.

［13］Moser B.On T-transitivity of kernels［J］.Fuzzy Sets and Systems，2006，157（13）：1787-1796.

［14］张翔，肖小玲，徐光祐.基于样本之间紧密度的模糊支持向量机方法［J］.软件学报，2006，17（5）：951-958.

［15］张秋雨，竭洋，李凯.模糊支持向量机中隶属度确定的新方法［J］.兰州理工大学学报，2009，35（4）：89-93.

Fuzzy rough support vector machine with dual membership.

HAN Hu，DANG Jianwu

School of Electronic and Information Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China

It is difficult for support vector machine to deal with uncertain information because SVM is not only sensitive to noises and outliers but also the inconsistence between conditional features and decision labels is not taken into account. In order to overcome the problem，two types of membership are introduced into standard support vector machine，one type of membership is computed by the distance between the training samples and their center as fuzzy membership，the other type of membership is computed by the distance between the training samples and the nearest training sample with different class label as rough membership.At last several comparative experiments are made to show the performance and the validity of the proposed approach.

support vector machine；uncertain problem；fuzzy theory；rough set

A

TP18

10.3778/j.issn.1002-8331.1311-0260

甘肃省自然基金（No.1308RJZA224）；兰州交通大学青年基金资助项目（No.2011024）。

韩虎（1977—），男，博士，副教授，主要研究方向：机器学习，数据挖掘；党建武，男，教授，博导，主要研究方向：神经网络，智能计算。E-mail：hanhu-lzjtu@163.com

2013-11-18

2014-02-28

1002-8331（2015）22-0150-04

CNKI网络优先出版：2014-04-01，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0260.html