基于卡尔曼滤波的无人机姿态测量研究*
袁 亮,楚仕彬
(新疆大学机械工程学院,乌鲁木齐 830047)
基于卡尔曼滤波的无人机姿态测量研究*
袁 亮,楚仕彬
(新疆大学机械工程学院,乌鲁木齐 830047)
文章针对无人机姿态测量中受制于计算机存储和处理每个参数字节的限制,使得计算精度也同样受到一定限制,舍入误差不可避免的存在于系统之中,对于卡尔曼滤波状态估计的误差可以由测量更新过程来修正,然而对误差协方差矩阵P却没有相应的修正,随着迭代次数不断增加,将导致P矩阵失真,打破其对角对称性。为提高无人机姿态测量的准确性,由此设计由陀螺仪、加速度计和磁强计组成的姿态测量系统,采用UD分解扩展卡尔曼滤波方法,实现对四元数的估计,并通过实验进行分析验证,实验结果表明该UD分解扩展卡尔曼滤波方法能够在低动态环境下准确解算出姿态角度,并能有效克服舍入误差的影响。
卡尔曼滤波;无人机;姿态测量
0 引言
在实际应用卡尔曼滤波的时候,我们需要存储大量的参数,并且需要进行大量的矩阵运算,在小型四旋翼无人机的控制中,主控制器的规格一般较低,并不能实现高精度的计算,只能采用精度较低(单精度32位)的算法来执行卡尔曼滤波。这使得舍入误差不可避免的存在于系统之中,随着迭代次数的增加,误差协方差矩阵P会逐渐失真,从而导致卡尔曼增益矩阵K失真。小的增益会使状态估计反应迟缓,大的增益会产生不稳定、动荡的状态估计。极端的协方差矩阵失真也能够导致软件系统的崩溃。因此在实际应用卡尔曼滤波的过程中,要尽可能的减小误差协方差矩阵计算的误差,特别是P必须保持正定。
为了消除舍入误差对滤波结果的影响,提高滤波精度,在实际应用中可以使用高精度算法(64位)来执行卡尔曼滤波,文献[1]中提出采用约瑟夫式的协方差更新,可以有效的提高计算精度,文献[15]提出采用平方根式的卡尔曼滤波,可以有效的提高计算精度,并且能够保持误差协方差的对称性和正定性。
1 系统组成及姿态解算原理
本文所采用的姿态测量系统主要由三轴加速度计、三轴陀螺仪和三轴磁强计组成。主控制器读取姿态测量传感器的数据,通过卡尔曼滤波对传感器测量数据进行融合处理,得到当前最优四元数,从而计算出无人机的姿态角度。

2 采用UD分解算法
受到处理器有效字长的限制,卡尔曼滤波在实际滤波过程中存在舍入误差积累,随着卡尔曼滤波运行次数不断增加,矩阵的失真就越大,从而出现误差协方差矩阵P不能保持正定性,滤波出现不稳定的情况[2]。
对P(n×n维)矩阵进行UD分解,即P=UDUT,其中U(n×n维)为单位上三角矩阵,且对角线元素为1,D(n×n维)为对角阵,P为对阵正定矩阵。并且产生唯一UD分解步骤如下:
(1)对于第n列,有
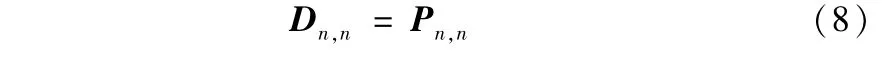
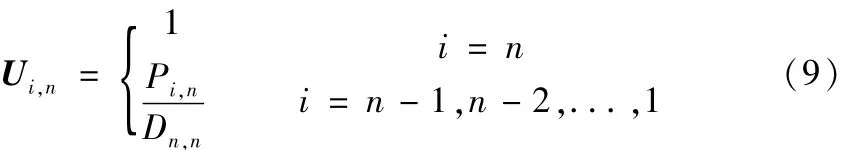
(2)对于其它列,j=n-1,n-1,...,1,有
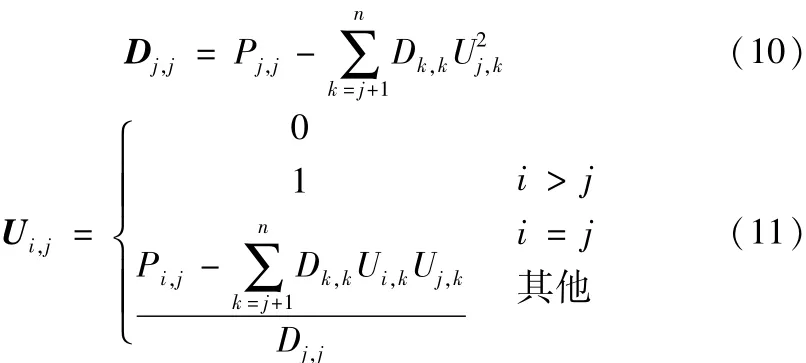
3 UD分解的扩展卡尔曼滤波算法
本卡尔曼滤波将四元数作为状态估计量,并且四元数更新采用三阶毕卡算法,与此同时将加速度计和磁强计的测量值作为观测量。滤波原理如图1所示。
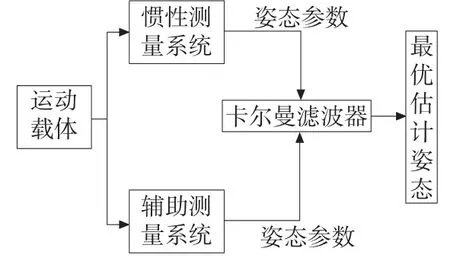
图1 卡尔曼滤波原理
3.1 卡尔曼滤波状态方程
目前求解四元数微分方程主要有两种方法:一种是四阶龙格库塔法,另一种就是本文所使用的三阶毕卡逼近法。其预测方程为:

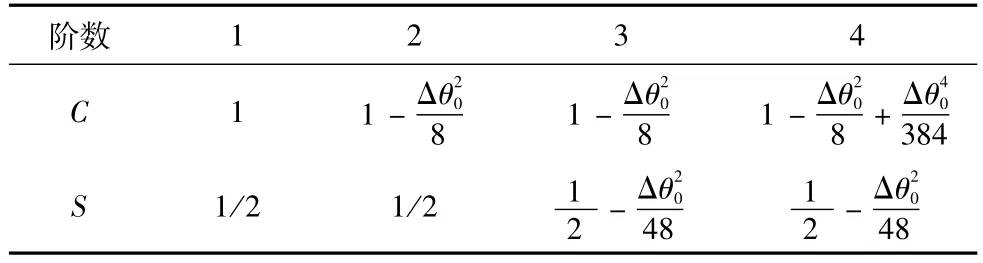
表1 毕卡各阶表达式

3.2 卡尔曼滤波观测方程
将加速度计和磁强计传感器测量的值作为观测量Z(t)。

3.3 采用UD分解算法的扩展卡尔曼滤波流程
根据卡尔曼滤波的原理,基于UD分解的扩展卡尔曼滤波流程如下:
UD分解算法的实现步骤。

上述过程即为采用UD分解算法的卡尔曼滤波的实现步骤,滤波器每次执行都按此过程循环。
(6)经过卡尔曼滤波之后,就能得到最优估计四元数,再通过式(3)便可得到姿态角度。
4 实验
4.1 实验准备及参数设定
为验证本文的算法,使用“第七实验室”的开发板captain,该开发板集成STM32405RG(主控制芯片)、MPU6050(三轴陀螺仪和三轴加速度计)、HMC5883(磁强计),同时该开发板具有丰富的通讯接口,能够将姿态数据通过UART上传至上位机进行分析。构建验证系统如表2所示。

表2 系统试验参数

表3 卡尔曼滤波参数初始化
4.2 软件实现
本软件开发平台为Keil uVision4,姿态测量过程分为系统初始化、姿态初始化、姿态更新三个过程,如图2所示。
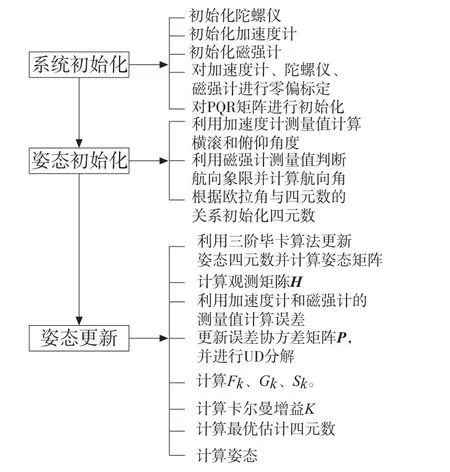
图2 姿态测量过程
根据参考坐标系定义,判断航向的象限如表4所示。

表4 航向象限的判断
4.3 实验结果
本实验采用一个能够实现匀速转动和加速转动的转台,动态测量姿态和传感器的数据,本实验数据的采集频率为100Hz,采集次数600次以上,为保证无人机飞行过程中能够稳定、可靠的飞行,姿态变化不超过±60°,本实验均是在此姿态范围内进行实验。图3和图4为静止时刻俯仰测量对比图,从图中我们可以看出,采用UD分解算法的扩展卡尔曼滤波测量值更为稳定和精确,能够有效的抑制舍入误差对系统稳定性的影响;图5为在匀速转动的情况下的对比图,从图中可以看出,在步进电机转动匀速改变姿态的过程中,采用UD分解算法的扩展卡尔曼滤波测量值更为稳定,在局部抖动的情况下,依然能够消除抖动,准确的测量姿态;图6为加速运动情况下的对比图,从图中可以看出,在加速运动的过程中,采用UD分解算法的扩展卡尔曼滤波能够较为准确的跟踪姿态,不会因加速运动出现剧烈的角度变化,未采用UD分解的算法虽然也能大体跟踪姿态,但是其抖动较为明显,不适宜在无人机上使用。
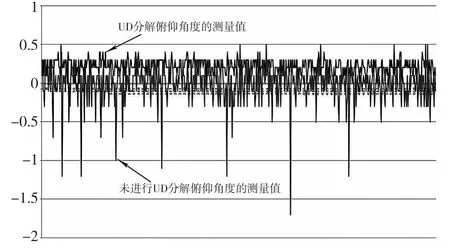
图3 静止时刻俯仰测量对比图
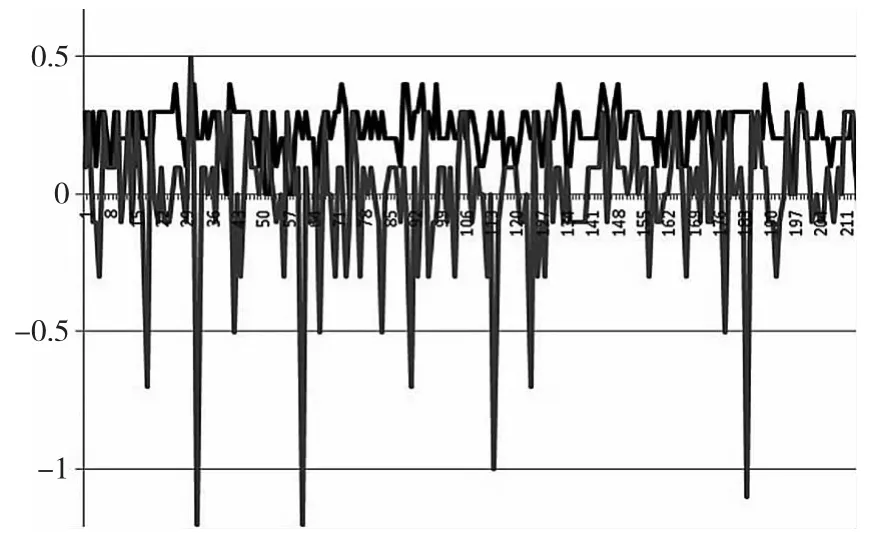
图4 静止时刻局部放大图
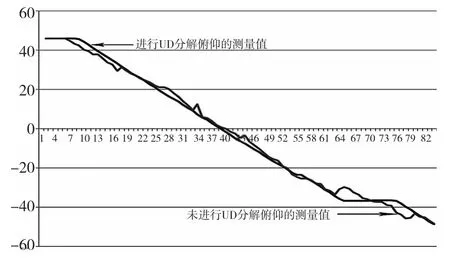
图5 匀速运动情况下的测量值
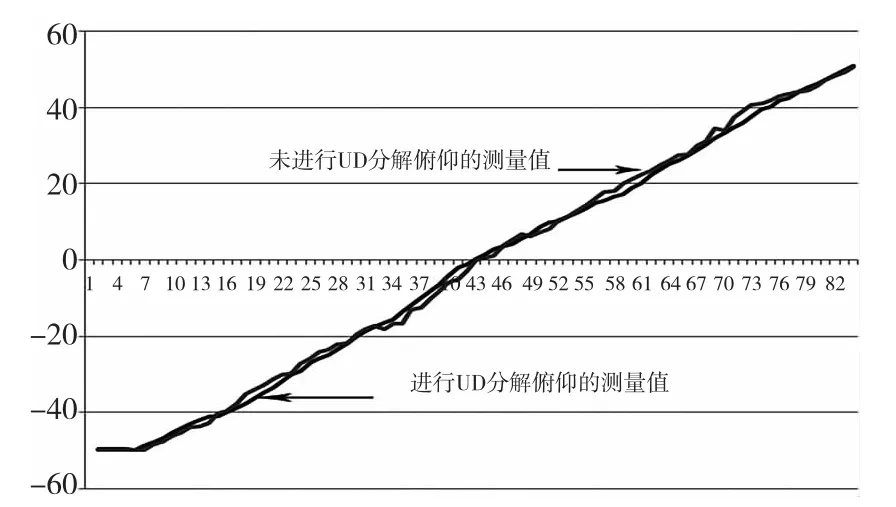
图6 加速运动情况下的测量值
5 结论
本文研究基于UD分解算法的扩展卡尔曼滤波在四旋翼无人机姿态测量中的应用,通过实验,发现采用UD分解算法的扩展卡尔曼滤波能够更为稳定的测量姿态,能够有效抑制舍入误差带来的影响,防止P矩阵发散,提高姿态测量精度。
[1]李涛,练军想,曹聚亮,等.GNSS与惯性及多传感器组合导航系统原理[M].北京:国防工业出版社,2011.
[2]冯鹏,邹世开.卡尔曼滤波器UD分解滤波算法的改进[J].遥测遥控.2005,26(1):10-14.[3]张秋阳.无人机姿态测算及其误差补偿研究[D].长沙:中南大学,2011.
[4]陈祖贵.UDU分解滤波算法及其应用[J].中国空间科学技术,1989(6):39-48.
[5]隋树林,袁健,张文霞,等.基于UD-EKF自主光学导航方法仿真[J].系统仿真学报.2007,19(3):482-485.
[6]A M Sabatini.Quaternion-based extended kal-man filter for determining orientation by inertial andmagnetic sensing[J]. 2006,53(7):1346-1356.
[7]李建文,郝顺义,黄国荣.基于UD分解的改进型强跟踪滤波器 [J].系统工程与电子技术.2009,32(8):1953-1957.
[8]E R Bachmann,IDuman,et.al.Orientation Trac-king for Humans and Robots Using Inertial Sensors[R].Robotics and Automation.1999:187-194.
[9]H J Luinge,P H Veltink.Measuring orien-tation of human body segments usingminia-ture gyroscopes and accelerometers[J].Medical and Biological Engineering and Computing.2006,43(2):273-282.
[10]王宏伟,马广富.基于正交最小二乘和UD分解的模糊建模方法[J].控制与决策,2003,18(6):758-763.
[11]XUE Liang,QIN Wei.et.al.Application of Quaternion Based Extended Kalman Filter for MAV Attitude Estimation Using MEMS Sensors[J].Nanotechnology and Preci-sion Engineering.7(2),2009.163-167.
[12]G.J.Bierman.Measurement updating using the U-D factorization[J].Automatic.1976,12:375-382.
[13]数学手册编写组.数学手册[M].1版.北京:高等教育出版社,1979.
[14]王学斌,徐建宏,张章.卡尔曼滤波参数分析与应用方法研究[J].计算机应用与软件,2012,29(6):212-215.
[15]Arasaratnam,Haykin.Square-Root Quadra-ture Kalman Filtering[J].signal processing IEEE.2008,56(6):5859-2593.
(编辑 李秀敏)
Research on UAV Attitude Calculation Based on Kalman Filter
YUAN Liang,CHU Shi-bin
(Mechanical Engineering Academy,Xinjiang University,Urumqi830000,China)
Subject to the limitations of computer storage and processing parameters of each byte,which makes the precision of calculation is also subject to certain restrictions,rounding errors inevitably exist in the system,the errors of Kalman filter state estimation can be corrected by the update process ofmeasured,but the error covariancematrix P can notbe corrected,along w ith the iteration number increased,the covariance matrix P w ill become distortion.It is diagonal symmetry w ill broken.In order to improve the attitudemeasurement accuracy of UAV,thus design the attitudemeasurement system composed of gyroscope accelerometer andmagnetometer,using themethod of UD decomposition EKF to data fusion to estimate Quaternion and verified by the experiment.The experimental results show that the UD decomposition EKFmethod can accurately calculate the attitude angle in low dynamic environment,and can effectively overcome the influence of rounding errors.
kalman filter;unmanned aerial vehicle;attitude estimate
TH165;TG659
A
1001-2265(2015)07-0110-04 DOI:10.13462/j.cnki.mmtamt.2015.07.030
2014-09-26;
2014-10-27
国家自然科学基金(61262059,31460248);新疆优秀青年科技创新人才培养项目(2013721016);新疆自治区科技支疆项目(201591102)
袁亮(1972-),男,乌鲁木齐人,新疆大学副教授,博士,研究方向为机器人控制技术,计算机图像处理,(E-mail)ylhap@163.com。

