基于自适应变异粒子群优化算法的产品装配序列规划*
陈海彬,郭建文,孙振忠,王 松,张智聪
(1.东莞理工学院机械工程学院 东莞 523808;2.华南理工大学机械与汽车工程学院 广州510640)
基于自适应变异粒子群优化算法的产品装配序列规划*
陈海彬1,郭建文1,孙振忠1,王 松2,张智聪1
(1.东莞理工学院机械工程学院 东莞 523808;2.华南理工大学机械与汽车工程学院 广州510640)
为提高产品虚拟装配序列规划水平,提出了面向装配序列规划的自适应变异粒子群优化算法。算法针对产品装配序列规划离散性的特点,在基本粒子群算法的基础上,对粒子位置、速度与粒子速度和位置更新操作进行了重定义,通过引入遗传算法中的变异算子来提高算法跳出局部最优的能力,同时改变惯性权重的取值方式以加快算法的收敛速度。以一柱塞泵的装配规划实例来分析该算法的性能,验证了自适应变异粒子群优化算法的可行性;与遗传算法和粒子群算法的比较证明自适应变异粒子群优化算法更有效。
自适应;变异粒子群;装配序列规划
0 引言
研究表明,在制造企业中装配费用占整个生产费用的比例大于40%,装配时间占整个工作时间的40%~60%[1]。装配规划是在确保装配可行的基础上,确定装配轨迹、顺序、辅助工具等装配方案。良好的装配规划能有效地提高装配质量和效率,降低装配成本[2]。装配序列规划[3](Assembly Sequences Planning,ASP)是装配规划的重要组成,其实质是在一定的约束条件下,从大量的可供选择的装配序列中确定满足需求(如时间、费用、可靠性等)的最优方案,可视为一种NP问题。
近年来,遗传算法[4]、蚁群算法[5]、模拟退火算法[6]、人工神经网络[7]、粒子群算法[8](Particle Swarm Optimization,PSO)等智能优化算法在ASP中得到应用。然而,当种群规模较小时,遗传算法收敛速度就会很慢,不易得到理想装配序列[9];模拟退火算法对解空间的拓展不够好,不容易搜索到最有效的区域,搜索效率低[10];人工神经网络算法缺乏全局搜索能力;蚁群算法在搜索后期容易出现停滞现象。相对于其它智能算法,粒子群算法是解决ASP的较优方法,但粒子群算法同样存在早熟收敛的不足[11]。
为此,本文提出基于自适应变异粒子群优化算法(Adaptive Particle Swarm Optimization Algorithm with Mutation,AMPSO)以解决产品装配序列问题。方法针对ASP离散性特点,重定义粒子位置、速度及位置和速度的更新操作,引入变异算子来保证算法不过早收敛。实验表明算法能有效提高ASP的效率和质量。
1 目标函数的构造
1.1 评估指标


2 基于AMPSO的产品装配序列
2.1 基本PSO算法的重定义

2.2 算法的改进及实现步骤
AMPSO算法通过加入变异算子,一方面可以提高算法的局部搜索效果;另一方面可以保持群体的个体差异性,防止早熟收敛现象的发生,增加了粒子最终收敛到全局最优解的概率。
(1)粒子初始化。ASP的解为一可行的装配序列矩阵AS,同时AS又由装配零件序列AP、装配方向序列AD和装配工具序列AT组成。随机初始化产生AP序列,由其确定最优AD和AT序列。
(2)初始适应度计算。根据式(4)可以直接计算各粒子的适应度函数值,并确定初始个体最优序列和初始全局最优序列。
(3)惯性权重计算。惯性权重ω按照式(7)取值:
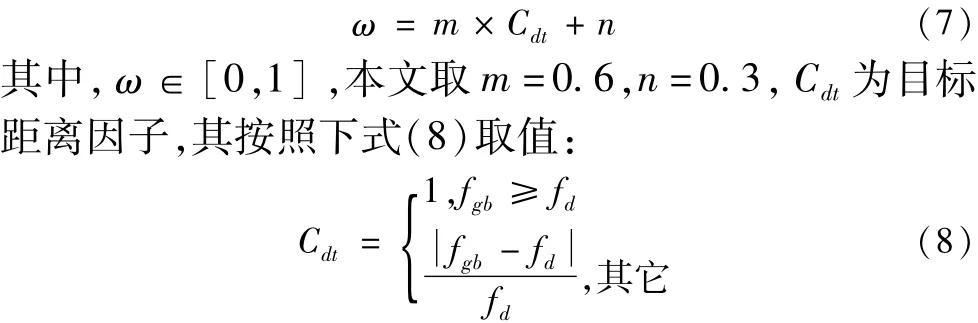
其中,fgb为目前找到的全局最优装配序列适应度函数值,fd为全局最优装配序列期望适应度函数值。
(4)粒子更新。装配零件序列AP根据式(5)和式(6)更新,而装配方向序列AD和装配工具序列AT则由更新后的AP序列得到,AD和AT序列为更新后的AP序列的最优序列。
(5)适应度更新。由公式(4)更新粒子群的适应度值,并更新各粒子的个体最优序列和全局最优序列。
(6)多样性因子更新。采用种群适应度值的标准方差σ作为衡量种群多样性的指标,其按照下式(9)取值:
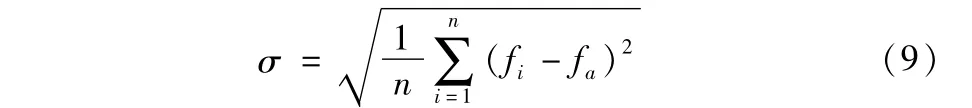
其中,n是粒子群的粒子数,fi是第i个粒子的适应度,fa为粒子群的平均适应度:
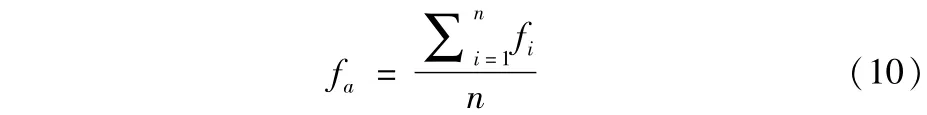
(7)变异。为避免早熟发生,特引入变异算子使得当前全局最优装配零件序列gBest发生变异,根据文献[13],变异概率pm计算公式如下:
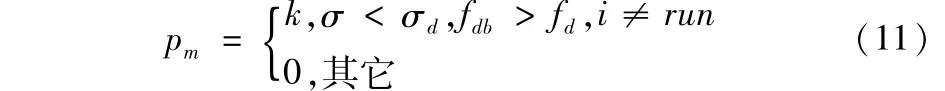
其中,k∈[0.1,0.3],σd为种群收敛临界标准差,其取值与实际问题有关,一般远小于σ的最大值,fd为期望最优适应度,i为当前迭代次数,run为最大迭代次数。当满足上述变异条件,而且满足fgb≥cf,则同时将随机生成的新种群替换旧种群。
(8)如果i<run,转到步骤3;否则转至步骤9。
(9)输出找到的最优序列gBest。
3 实例及比较分析
3.1 应用实例
图1为柱塞泵模型。模型由14个零件和子装配体组成,各零件可用装配工具如下所示:P1(T1)、P2(T2/T3)、P3(T2/T3)、P4(T2/T3)、P5(T2)、P6(T2)、P7(T1/T2)、P8(T2)、P9(T1)、P10(T3)、P11(T2)、P12(T2)、P13(T1)、P14(T3)。参数设置:cf=5,cs= 0.5,ct=0.2,cd=0.3,c1=0.5,c2=0.5,σd= 0.1,fd=2.1,k=0.2,sizepop=100,run=600。
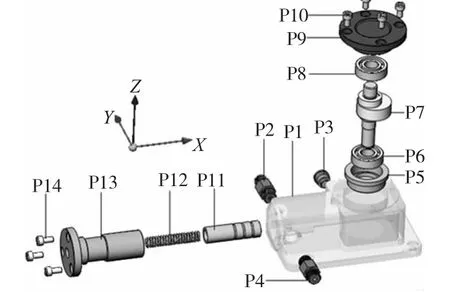
图1 某柱塞泵的三维实体模型
通过多次试验分析,全局最优适应度值为2.1,但全局最优装配序列有多个,如下序列为其中一个:P1(-Z&T1)→P5(-Z&T2)→P6(-Z&T2)→P7(-Z&T2)→P8(-Z&T2)→P11(+X&T2)→P12(+X&T2)→P13(+X&T1)→P9(-Z&T1)→P10(-Z&T3)→P14(+X&T3)→P4(+Y&T3)→P2(-Y&T3)→P3(-Y&T3)。
图2是50次试验各代平均适应度和最优适应度的平均值变化趋势;50次试验中有多次获得全局最优适应度值2.1。图3是其中一次试验的各代最优适应度和平均适应度的变化趋势。
从图2可以看出,50次试验中,第0代平均适应度均值为26.9501,而最优适应度均值为12.558,可见初始随机生成的装配序列整体质量较差,而且存在较多的不可行装配序列,但在算法结束的时候平均和最优适应度均值都能得到较好的结果,这说明该算法对初始装配序列的质量要求不高,对装配序列是否可行没有依赖。同时,从图2中还可以看出,最优适应均值和平均适应度均值稳步下降。从图3可以看出,平均适应度值发生了多次局部跳跃增大的现象,这是因为当前种群多样性较弱,陷入了局部最优,根据变异机制,发生了变异,种群得到了更新,增强了种群的多样性。从最优适应度和平均适应度曲线最终重合可知,种群经过多次变异之后最终收敛。
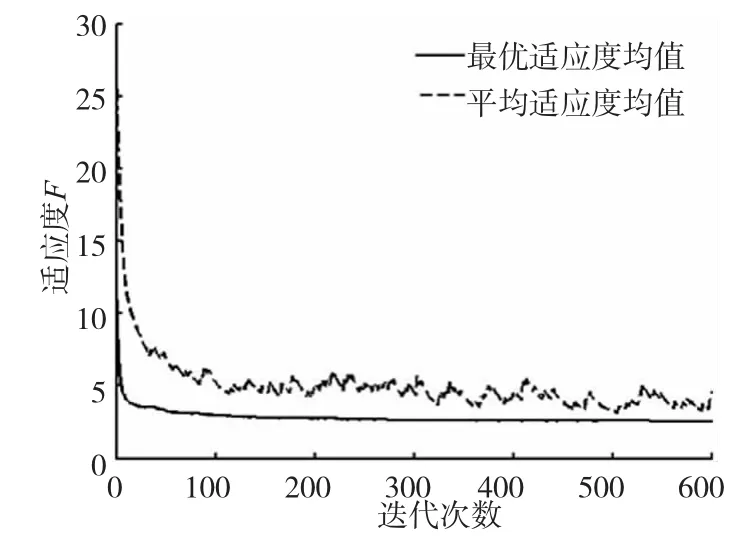
图2 平均和最优适应度的平均值
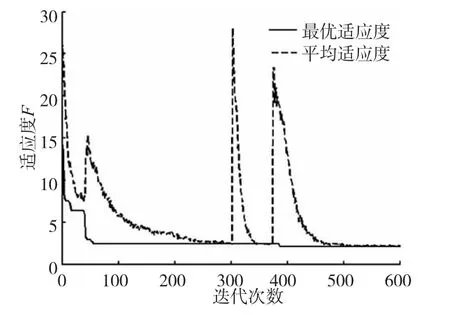
图3 最优和平均适应度
3.2 算法比较分析
为了验证AMPSO算法的有效性和优越性,现将AMPSO算法与遗传算法(Genetic Algorithm,GA)和PSO算法相比较。现仍然采用上述的相同实例进行装配序列规划,仿真环境和算法参数不变。其中GA的交叉概率取为0.8,变异概率为0.1,PSO算法的惯性权重取值为0.6。现比较三种算法迭代次数为600,重复运行次数为50,种群规模分别为20、50和100情况下的性能。

表1算法试验结果对比
从表1可以看出,在50结果中,AMPSO和PSO算法都能得到较多的可行装配序列,但是在种群规模较小的情况下,遗传算法将会得到较少的可行装配序列,且种群规模与可行序列数呈正相关;在相同种群规模下,AMPSO和PSO算法找到的最优装配序列比GA好;在不同种群规模下,GA始终没有找到全局最优解,而PSO和AMPSO算法可以有效的找到全局最优解,并且AMPSO算法找到全局最优解的个数要明显多于PSO,这说明AMPSO算法有着最强的寻找全局最优解的能力;在运行时间上,AMPSO和PSO算法要略多于GA。
本文以适应度函数值的标准方差为衡量种群多样性的指标,比较三种算法的种群适应度函数值得标准差均值随着迭代次数增加的变化情况,三种算法在种群规模为100,重复运行50次情况的下种群多样性对比曲线如下图4所示。
通过图4可以看出,遗传算法的多样性一直没有太大变化,这说明其收敛速度慢,而算法迭代次数的前部分AMPSO有着比PSO更快的收敛速度,但是在后期其波动较大,这是由于AMPSO算法加入了变异因子,当种群陷入局部最优时,根据变异机制,种群发生了变异,改善了种群的多样性,从而加大了算法收敛到全局最优解的概率,从全局看,AMPSO和PSO算法的种群多样性都稳步下降。

图4 种群多样性对比
4 结束语
本文在基本PSO算法的基础上,对粒子位置、速度与粒子速度和位置更新操作进行了重定义,并且通过引入GA中的变异算子来提高算法跳出局部最优的能力,提出了一种基于AMPSO的ASP方法。仿真实例结果表明:与GA和基本PSO对比,该算法具有收敛速度快、寻优能力强和能有效避免陷入局部最优解的优点,能有效提高产品装配序列规划的效率和质量。
[1]王峻峰,李世其,刘继红,等.计算机辅助装配规划研究综述[J].工程图学学报,2005(2):1-5.
[2]宁黎华,古天龙.装配序列规划问题求解的一种混合算法[J].计算机集成制造系统,2007,13(4):762-767.
[3]李原,张开富,王挺,等.基于遗传算法的飞机装配序列规划优化方法[J].计算机集成制造系统,2006,12(2):188-191.
[4]LAZZERINI B,MARCELLONI F.A genetic algorithm for generating optimal assembly plans[J].Artificial Intelligence in Engineering,2000,14(4):319-329.
[5]Mingxing Deng,Qiuhua Tang,Zhe Lei.An improved assembly sequence planning approach using ant colony algorithm[J].International Review on Computers and Software,2011,6(7):1307-1312.
[6]MILNER JM,GRAVESSC,WHITNEY D E.Using simulated annealing to select least-cost assembly sequences[C]//Proceeding of IEEE International Conference on Robotics and Automation.San Diego,1994(3):2058-2063.
[7]HONG D S,CHO H S.A neural network based computational scheme for generating optimized robotic assembly sequences[J].Engineering Application Artifical Intelligence,1995,8(2):129-145.
[8]Kennedy J,Eberhart RC.Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks.Perth:IEEE,1995:1942-1948.
[9]于嘉鹏,王成恩,王健熙.基于最大-最小蚁群系统的装配序列规划[J].机械工程学报,2012,48(23):152-166.
[10]曾冰,李明富,张翼,等.基于萤火虫算法的装配序列规划研究[J].机械工程学报,2013,49(11):177-184.
[11]吕振肃,侯志荣.自适应变异的粒子群优化算法[J].电子学报,2004,32(3):416-420.
[12]刘继红.复杂产品协同装配设计与规划[M].武汉:华中科技大学出版社,2011.
[13]刘卫宁,李一鸣,刘波.基于自适应粒子群算法的制造云服务组合研究[J].计算机应用,2012,32(10):2869-2874.
(编辑 李秀敏)
Product Assem bly Sequences Planning Based on Adaptive Particle Swarm Optim ization Algorithm w ith M utation
CHEN Hai-bin1,GUO Jian-wen1,SUN Zhen-zhong1,WANG Song2,ZHANG Zhi-cong1
(1.SchoolofMechanical Engineering,Dongguan University of Technology,Dongguan 523808,China;2.School of Mechanical&Automotive Engineering,South China University of Technology,Guangzhou 510640,China)
In order to improve the level of product virtual assembly sequence planning,the productassembly sequences planning based on adaptive mutation particle swarm optimization algorithm is proposed.In view of the discreteness characteristic of the product assembly sequences planning,on the basis of the basic particle swarm optim ization algorithm,the particle position,velocity and their update operation are redefined,themutation operator of genetic algorithm is introduced to improve the ability to jump outof local optimum,at the same time,by changing the value of inertia weightway to accelerate the algorithm convergence rate. The characteristics of adaptive particle swarm optim ization algorithm w ithmutation are showed via assembly planning experiment of a plunger pump.The experiment proved thatadaptive particle swarm optim ization algorithm w ith mutation is feasible,and the efficiency of adaptive particle swarm optimization algorithm w ith mutation is compared w ith the efficiency of genetic algorithm and particle swarm optim ization algorithm,the experiment show that the adaptive particle swarm optimization algorithm w ith mutation ismore efficient.
self-adaption;mutation particle swarm;assembly sequences planning
TH166;TG506
A
1001-2265(2015)07-0153-04 DOI:10.13462/j.cnki.mmtamt.2015.07.043
2015-01-19;
2015-03-30
国家自然科学基金项目(71201026);广东省教育厅科技创新项目(2013KJCX0179);东莞市社会科技发展项目(201310810101);东莞市高等院校、科研机构科技计划一般项目(2014106101007)
陈海彬(1984-),男,广东省汕尾人,东莞理工学院工程师,研究方向为数控与特种加工遥控维护规划研究;通讯作者:孙振忠(1969-),黑龙江肇源人,东莞理工学院教授,硕士生导师,研究方向数字化制造,(E-mail)hbchen@dgut.edu.cn。

