基于BP神经网络的大型螺纹旋风铣削表面粗糙度预测*
周 斌,曹 勇,王禹林,冯虎田
(南京理工大学机械工程学院,南京 210094)
基于BP神经网络的大型螺纹旋风铣削表面粗糙度预测*
周 斌,曹 勇,王禹林,冯虎田
(南京理工大学机械工程学院,南京 210094)
大型螺纹旋风铣削加工后的螺纹滚道表面粗糙度是影响其各项服役性能的关键因素之一。考虑到螺纹旋风铣削加工过程中表面粗糙度影响因素及螺纹圆弧形滚道结构特殊性,提取浮动支撑下降区域螺纹滚道侧表面的粗糙度值,建立基于BP神经网络的表面粗糙度预测模型,并通过对比模型预测值与试验值验证预测模型的精度。结果表明:BP神经网络模型的预测精度较高,预测误差在5%以内,最高可达到约1%。
螺纹旋风铣削;表面粗糙度;BP神经网络;预测模型
0 引言
大型螺纹旋风铣削加工过程中的工件多点变浮动支撑约束、多刀具周期性断续渐进成型切削等特点将影响加工后螺纹工件的螺纹滚道表面粗糙度;特别是在浮动支撑下降区域,因约束条件减少导致加工过程中动态响应相对于其他区域加剧,从而降低了螺纹工件加工后的表面粗糙度。而零件表面粗糙度是影响疲劳强度、接触刚度、摩擦磨损以及零件之间的配合等服役性能的关键因素,是评定零件加工质量的重要指标之一[1]。因此研究螺纹加工过程中浮动支撑下降区域表面粗糙度并建立预测模型尤其重要。建立精确的表面粗糙度预测模型,实现对硬旋铣螺纹滚道表面粗糙度的优化控制,有助于在实际生产前对表面粗糙度进行预测,从而保证螺纹的加工质量和加工效率,减少废品的出现,降低生产成本。
目前,国内外金属切削表面粗糙度的预测方法主要有理论建模法、设计试验法和人工智能法[2]。在多因素藕合作用下,利用理论建模法建立表面粗糙度预测模型的难度高、误差大、精度低[3-5]。设计试验法则无法对未加工过的工艺参数组合进行准确的预测。曹勇[6]等通过大型螺纹高速旋风铣削试验分析了各主要切削参数对螺纹滚道表面粗糙度的影响规律及影响因素进行了研究,但其未对其粗糙度进行预测。而人工智能法因其具有良好的任意非线性映射能力、自组织和自学习等优点被广泛应用于表面粗糙度的预测模型中[7]。其中,BP神经网络算法采用误差反向传播(Back Propagation)学习算法,因其具有很强的非线性处理能力并且预测精度较高而备受青睐。陈廉清等[8]针对外圆磨削中表面粗糙度的影响因素多、监测困难的问题提出了遗传算法与反向传播神经网络结合的表面粗糙度预测模型,并通过试验进行了验证。李波等[9]用BP神经网络的方法对高效深磨加工工程陶瓷Al2O3的工件表面粗糙度进行了训练、预测和分析。高腾等[10]提出一种基于BP神经网络的表面粗糙度在线辨识方法并且仿真和试验表明基于BP神经网络模型能够很好地预测表面粗糙度。
上述研究成果对螺旋螺纹滚道表面粗糙度的预测提供了很好的理论指导和借鉴意义。然而大型螺纹旋风铣削是圆弧型渐进铣削过程,与普通切削加工不同,因此,为预测旋铣加工过程中浮动支撑下降区域的螺纹滚道表面粗糙度,建立了基于BP神经网络的表面粗糙度预测模型,并通过试验验证模型的预测精度。结果表明,所建立的预测模型精度较高,该预测模型可为同类型的表面粗糙度预测提供一定的借鉴。
1 试验条件
如图1所示,以陕西汉江机床自主研发的HJ092× 80螺纹硬态旋风铣床开展螺纹旋风铣削试验,工件材料为GCr15,长度为4m,直径80mm。为研究浮动支撑下降区域的表面粗糙度,开展了切削速度、切削深度、抱紧系数及刀具个数的单因素工艺参数试验,共计进行了20组,具体数据可见表1。

图1 陕西汉江HJ092×80螺纹硬态旋风铣床

表1 预测模型所需的样本参数表
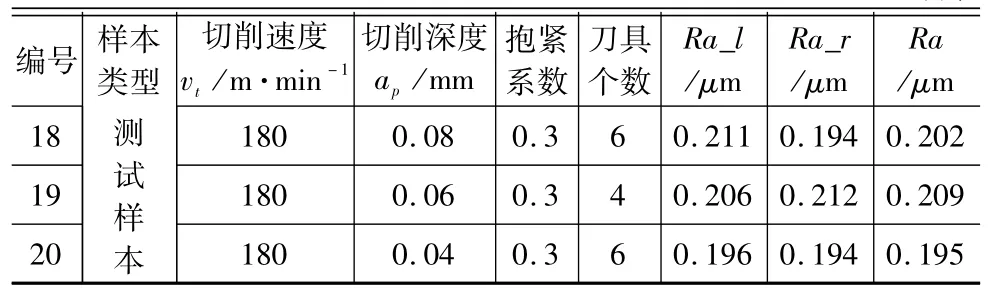
续表
由于螺纹类圆弧型滚道结构的特殊性并且丝杠副在服役过程中主要是螺纹滚道侧表面与滚珠接触,因此采用英国Taylor Hobson公司研制的白光干涉仪对螺纹滚道侧表面进行检测,其测量原理为非接触式测量,Ra重复精度≤3pm。为检测其滚道侧面的表面粗糙度,将螺纹工件倾斜15°,对滚道侧面表面粗糙度重复测量三次取平均值。
2 基于BP神经网络的表面粗糙度预测模型
2.1 BP神经网络
BP神经网络模型主包括输入层、隐层和输出层,模型的精度关键在于建立输入与已知的输出之间的一个满意关系及隐层的层数及节点数确定。输入层为4节点分别代表切削速度、切削深度、抱紧系数及刀具个数,输出层1节点代表预测的粗糙度,其模型结构如图2所示。

图2 神经网络预测模型图
为得到纯量,即将有量纲的物理量转化为无量纲,消除试验样本中奇异数据,在神经网络开始训练和测试前通常进行输入和目标输出数据的归一化,其算法如下

式中,dmax为输入和输出数据的最大值,dmin为输入和输出数据的最小值,di为第i个输入和输出数据。
较多的隐层数目可提高预测精度,但同时会带来网络复杂化和训练时间增加等问题。单个隐层可提供较的表面粗糙度预测精度,且网络简单、便于训练[11],故将隐层个数确定为1。结合神经网络模型图可知单个隐层的第K个节点的输入为:

其中,Ci,k为输入层节点与隐层节点的网络权值,θk为隐层节点的阈值,其中k≤m,m为隐层节点数目。
输出层第z个节点的输入为:
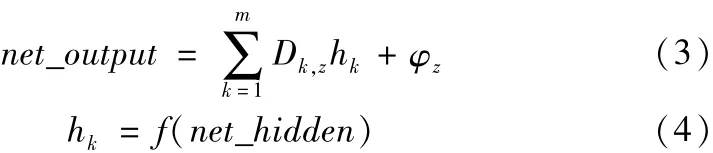
式中,φz是输出层节点的阈值,hk是隐层节点的输出,Dk,z是神经网络输出层节点与隐层节点之间的网络权值,f是隐层传递函数,通常为双曲正切S型函数。

输出层节点的输出为:

式中,Rp为螺纹滚道表面粗糙度人工网络模型的预测值,g为输出层传递函数,通常取线性函数。

输出层螺纹滚道误差函数为:

式中,Re为表面粗糙度的试验测量值。
BP神经网络模型的具体建立过程见图3,在matlab中建立BP神经网络预测模型通常选MSE作为性能函数,其训练精度MSE=1x10-3。
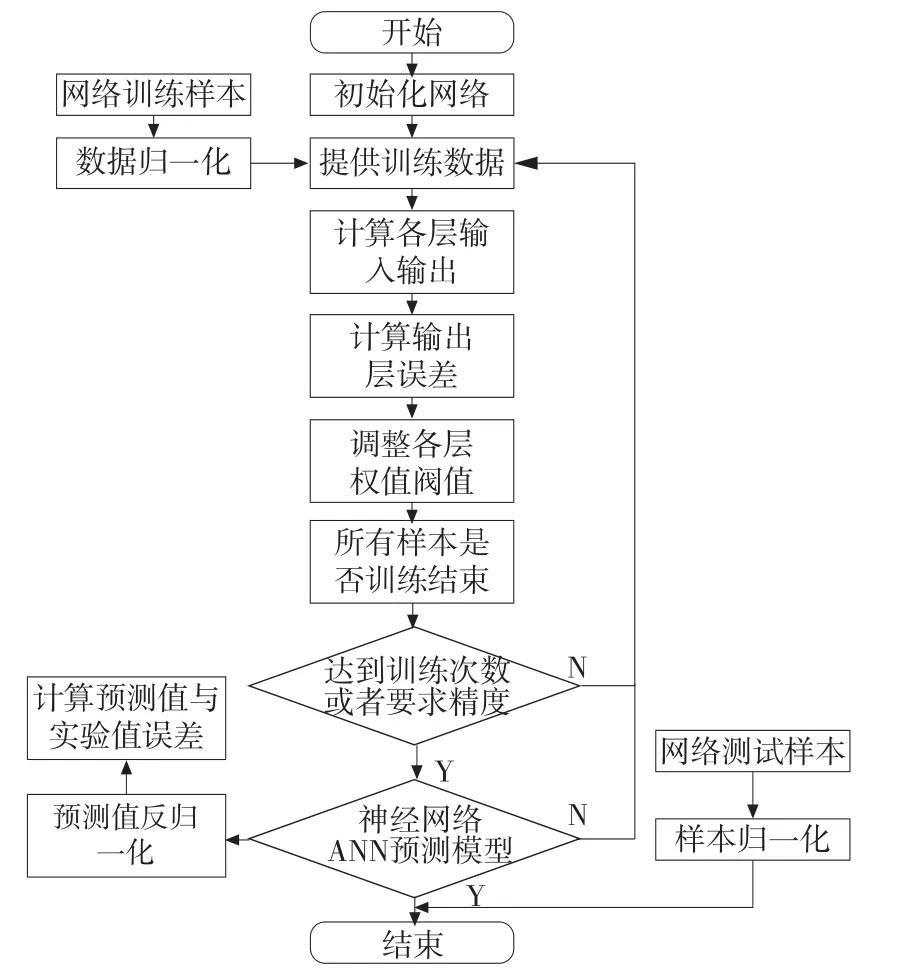
图3 神经网络预测模型算法
2.2 表面粗糙度值预测样本值的提取
为提高各表面粗糙度预测模型的精度和实现各预测模型的预测精度的对比,在浮动支撑下降区域内选取相同个数和切削工艺参数的训练样本和测试样。在建立预测模型之前,对样本中存在明显异常的试验数据点进行剔除处理,将剩下的样本合理分配为训练样本和测试样本,最终结果为训练样
本与测试样本之比为17:3。样本参数见表1,其中Ra_l、Ra_r、Ra分别表示左侧、右侧及左右侧平均粗糙度试验值。
2.3 表面粗糙度预测模型
依据式(1),首先对表1的训练样本和测试样本进行归一化处理,其中最大训练次数选为1000,神经网络预测模型基本参数见表2。经17组训练样本训练14次后,所有训练样本误差达到预先设定的精度0.001,即神经网络模型建立完成。

表2 神经网络结构参数及函数
3 表面粗糙度预测模型误差分析
针针对于所建立的各预测模型,将螺纹滚道表面粗糙度的预测误差定义为:

上式中,为预测误差值,Ra为试验值,Rp表示螺纹滚道粗糙度神经网络预测值。将表1的测试样本代入所建立的预测模型中,求出相应的预测值和预测误差,具体结果见表3,预测值与试验值的变化见图4。通过对比测试样本的试验值和预测值之间的误差来反映各预测模型的预测效果。

表3 螺纹滚道侧表面的表面粗糙度预测值及预测误差

图4 螺纹滚道表面粗糙度试验值和预测值对比
通过表3和图4可知发现无论是左侧、右侧还是整个螺纹滚道的粗糙度,BP神经网络模型的预测精度均较高,预测误差在5%以内,最高可达到约1%,并基本符合试验值的变化趋势。
4 结论
为预测大型螺纹旋风铣削加工过程中浮动支撑下降区域的表面粗糙度,考虑了切削速度、切削深度、抱紧系数及刀具个数对螺纹滚道表面粗糙度的的影响,建立基于BP神经网络螺纹滚道表面粗糙度预测模型,并通过试验验证模型的预测精度。结果表明:BP神经网络模型的预测精度均较高,预[参考文献]
测误差均在5%以内,最高精度可达到约1%。该预测模型可为同类型的表面粗糙度预测提供一定的借鉴。
[1]黄树涛,贾春德,姜增辉,等.高速车铣已加工表面粗糙度的理论与实验研究[J].哈尔滨工业大学学报,2005,37(5):717-720.
[2]段春争,郝清龙.切削加工表面粗糙度预测方法[J].组合机床与自动化加工技术,2013(8):4-7.
[3]D K,Ko T J,Kim H S.Optimization of feedrate in a face milling operation using a surface roughnessmodel[J].International Journal of Machine Tools and Manufacture,2001,41(3):451-462.
[4]Liu J.Prediction of surface roughness in CNC turning physical simulation[C]//Artificial Intelligence,Management Science and Electronic Commerce(AIMSEC),2011 2nd International Conference on.IEEE,2011:4127-4129.
[5]Lee K Y,Kang M C,Jeong Y H,et al.Simulation of surface roughness and profile in high-speed end milling[J]. Journal of Materials Processing Technology,2001,113(1):410-415.
[6]李隆.基于振动的大型螺纹旋风铣削建模与工艺试验研究[D].南京:南京理工大学,2013.
[7]曹勇,王禹林,冯虎田.大型螺纹硬态旋风铣削的表面粗糙度试验研究[J].组合机床与自动化加工技术,2015(1):26-29.
[8]陈廉清,郭建亮,杨勋,等.基于进化神经网络的磨削粗糙度预测模型[J].计算机集成制造系统,2013,19(11):2854-2863.
[9]李波,郭力.基于BP神经网络的表面粗糙度声发射预测[J].精密制造与自动化,2009(1):10-14.
[10]高腾,苗鸿宾,江敏.基于人工神经网络BTA钻削时表面粗糙度的预测[J].组合机床与自动化加工技术,2014(4):4-10.
[11]王俊平,李加彦.BP神经网络的学习过程与算法分析[J].计算机光盘软件与应用,2014(4):243-245.
(编辑 李秀敏)
Prediction of Surface Roughness of Large-scale Thread Hard Whirling Based on BP Neural Network
ZHOU Bin,CAO Yong,WANG Yu-lin,FENG Hu-tian
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)
Themachined surface roughness of large-scale thread hard whirling is the critical factor to influence the service performance.Considering the influence factors of surface roughness in the process of thread hard whirling and the special structure of thread arc-shaped raceway,surface roughness values of thread side raceway in falling area of floating support was obtained and the prediction model of surface roughness was provided based on BP neural network.Then prediction accuracy of themodelwas verified by contrasting the predictive value and the experimental value.The results show that BP neural network model has a relatively high prediction accuracy,prediction error is less than 5%and can up to 1%.
thread hard whirling;surface roughness;BP neural network;prediction model
TH162;TG506
A
1001-2265(2015)07-0005-03 DOI:10.13462/j.cnki.mmtamt.2015.07.002
2015-01-12;
2015-02-05
国家自然科学基金面上项目(51475244);江苏省"六大人才高峰"资助项目(2014-ZBZZ-006);中央高校基本科研业务费专项资金资助(30920130111001);南京理工大学“卓越计划”“紫金之星”(2015-zijin-07)
周斌(1991-),男,安徽宣城人,南京理工大学硕士研究生,研究方向为硬态切削技术,表面完整性,可靠性,(E-mail)zb_nust@163. com;通讯作者:王禹林(1981-),男,南京人,南京理工大学教授,研究方向为硬态切削,精密测控技术,可靠性技术,(E-mail)wyl_sjtu @126.com。

