基于分子动力学方法的孪晶银纳米线拉伸形变模拟

孙寅璐 高亚军 孙 倩 赵健伟

（南京大学化学化工学院，生命分析化学国家重点实验室，南京 210023）

基于分子动力学方法的孪晶银纳米线拉伸形变模拟

孙寅璐 高亚军 孙 倩 赵健伟*

（南京大学化学化工学院，生命分析化学国家重点实验室，南京 210023）

采用分子动力学方法研究了具有不同孪晶界密度的＜111＞晶向孪晶Ag纳米线在拉伸载荷下的形变行为, 讨论了孪晶界对纳米线力学强度的影响, 并分别阐明具有不同孪晶界密度Ag纳米线的塑性形变机理. 结果表明, 与单晶Ag纳米线的强度进行对比可知, 基于不同的形变模式, 孪晶界的引入对纳米线可以起到弱化作用或者强化作用. 以孪晶片层厚度的倒数（1/TBS）作为临界值, 当1/TBS小于0.2 nm-1时, 孪晶界作为位错源, 表现为对纳米线的弱化作用； 当1/TBS大于0.2 nm-1时, 孪晶界阻碍位错运动表现为强化作用. 强化作用机理分为两种： 当1/TBS介于0.2到0.5 nm-1时, 形变机理以孪晶界和位错相互作用为主, 断裂开口均在纳米线内部产生, 随着位错增殖形成孔洞, 进而向四周蔓延； 当1/TBS大于0.5 nm-1时, 孪晶界发生迁移以容纳位错活动, 位错不断增殖穿过孪晶界形成剪切带, 进而导致纳米线的颈缩. 由孪晶界密度不同引起的强化作用和弱化作用均随温度升高而减弱.

分子动力学； 银纳米线； 孪晶界密度； 拉伸载荷； 形变

1 引 言

金属纳米材料因其独特的机械性质、光电性质、热学性质和磁性质等，被广泛应用于电极材料、光学材料和催化材料等领域. 这些优异的性能与纳米晶粒中的高密度晶界及晶界原子的结构密切相关.1，2为了构建高强度纳米线，研究者们对关于晶界对纳米线的形变影响展开了大量的研究. 其中，孪晶界是一种特殊的晶界，晶界上下两部分关于孪晶界面对称，这种特殊结构常见于贵金属材料中.孪晶结构可使材料表现出良好的热稳定性和力学稳定性，尤其当材料尺寸减小到纳米级别时，界面原子的比例增加，孪晶界的作用愈发凸显，因此研究孪晶界对金属纳米线的形变影响显得十分必要.

实验上已经证实了高密度孪晶Cu纳米线具有极高的强度和拉伸塑性，这与孪晶界和位错的相互作用有关.3卢柯等4-7使用脉冲电沉积技术制备了高密度生长的孪晶Cu样品，其屈服强度高达900 MPa（比粗晶Cu高一个数量级），拉伸延展率可达13.5%.8研究表明，孪晶带宽（TBS）对纳米线的力学影响至关重要. 当TBS为15 nm时可获得最高的拉伸强度；当TBS ＞ 15 nm时，生长位错较少，孪晶界阻碍位错生长和运动实现强化，TBS越小阻碍效果越明显，因而纳米线强度增加； 当TBS ＜ 15 nm时，生长位错急剧增加，且随TBS减小而增多，生长位错分布在孪晶界周围成为位错源，故强化效用被掩盖.

理论上通常借助分子动力学模拟来研究孪晶界通过阻碍位错运动进而实现强化作用的机理.9-15大量的模拟研究表明，孪晶界密度能控制金属纳米线的力学性质和形变行为. Cao和Wei等16用分子动力学方法研究了＜111＞晶向孪晶Cu纳米线的形变机理，其研究表明孪晶片层厚度越小，孪晶纳米线的屈服应力越大. Deng和Sansoz17，18提出了相似的模拟模型，并且预测了不同尺寸的孪晶Cu纳米线其屈服应力和单位长度内的孪晶界个数成线性关系. 在拉伸塑性形变过程中，孪晶界既能作为位错源又能阻碍位错移动. Guo和Xia12根据动力学速率理论建立分析模型并讨论了二者的竞争关系. 此外Deng和Sansoz19进一步考虑了温度效应，提出了速控形变机理描述表面位错发射和孪晶界-滑移的相互作用.

尽管研究者们对孪晶纳米线的弹性形变和初始塑性形变已经展开了大量的分子动力学模拟研究，但是迄今为止，关于孪晶界对金属纳米线的形变影响仍不清晰. 大多数研究主要强调TBS的增强作用，而Deng和Sansoz20指出TBS也会弱化纳米线.最近，Jang等21报道了包含高密度孪晶界的Cu纳米柱原位试验，他们发现TBS不同导致了塑性形变的显著差异. TBS为0.6 nm时表现为韧性形变，而TBS为4.3 nm时表现为脆性形变. 可见，关于TBS对孪晶纳米线的结构和力学性质等方面的认识还不完整，仍需进一步阐明. 为了全面研究TBS对金属纳米材料力学性质的影响，在之前的研究中我们引入晶粒的长径比来表达TBS的概念，并且证实当TBS较大（长径比大于1）时，孪晶界对纳米线起到弱化作用，而当TBS较小（长径比小于1）时，孪晶界对纳米线起到强化作用.22文中虽然综合分析了孪晶界和晶粒尺寸对Ag纳米线的影响，但对于机理的阐述还不够深入. 为此，本文实施了不同孪晶界密度的Ag纳米线拉伸模拟，系统分析了随孪晶界密度增加其内在机理的转变机制，并进一步提出了导致强化作用的两种形变模式，为构建高强度纳米线打下理论基础.

2 模拟方法

构建了立方结构的FCC构型轴向为［111］晶向的孪晶Ag纳米线. 孪晶尺寸为6.7 nm × 6.7 nm × 28.33 nm，侧面为｛110｝面和｛112｝面. 包含的孪晶界（TB）个数范围从1到59，相应的TBS范围从0.47 到14.17 nm. 图1给出其中四种孪晶结构的初始构型，（a）、（b）、（c）和（d）分别代表TB数为1、5、14和39，相应的TBS分别为14.17、4.72、1.89和0.71 nm.（e）为同尺寸的理想单晶Ag纳米线，作为孪晶结构的对比研究. 体系的原子总数均在8万左右. 图中绿色原子代表表面原子，蓝色原子代表内部的FCC原子，粉色原子代表孪晶界原子. 采用Johnson解析的分析型Ag-Ag EAM势23来描述原子间相互作用，Verlet leapfrog数值积分法24获得原子的速度和运动轨迹. Nose-Hoover方法25，26控制体系温度，保持体系温度为10 K. 为了模拟真实体系，计算中x、y、z方向均采用自由边界条件. 时间步长为2.6 × 10-15s. 体系首先在10 K下自由弛豫2万步，待达到平衡后，沿［111］晶向（z轴）以0.058% ps-1的应变速率匀速双向拉伸直至断裂. 全部模拟计算均是在自主开发的大规模分子动力学仿真平台NanoMD软件27的支持下完成的，该软件的可靠性已经从大量的模拟研究中得到证实.28-34

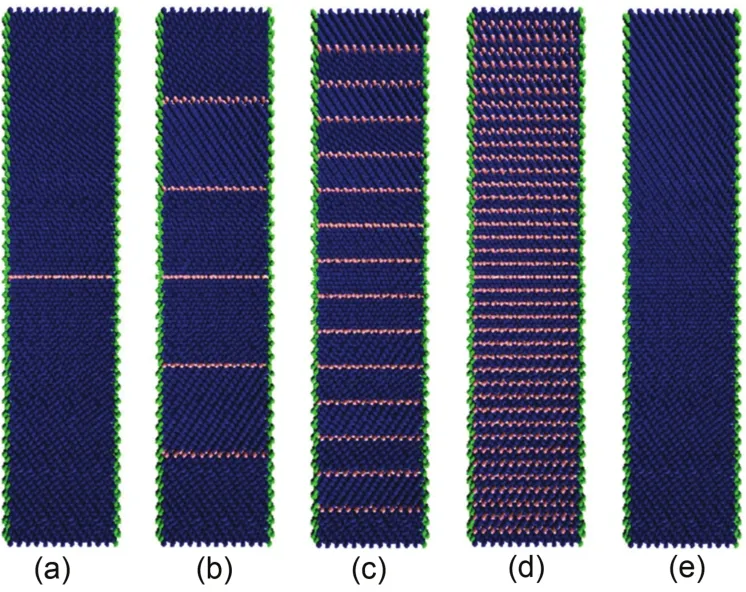
图1 ［111］晶向的孪晶Ag纳米线（NWs）的初始构型截面图Fig.1 Cross-sectional views of initial configurations of［111］ twinned Ag nanowires （NWs）

3 结果与讨论

3.1 形变过程的宏观性质分析

金属纳米线的宏观力学性质主要通过分析应力应变曲线得出. 图2为五种Ag纳米线拉伸载荷下的应力应变曲线. 各纳米线应力均随应变线性增加直至到达弹性极限. 线性部分斜率基本保持不变，说明孪晶界的存在不会影响纳米线的杨氏模量，这与之前实验观察到的结果一致.29计算的杨氏模量约为98.4 GPa，实验值为（102 ± 23） GPa，比粗晶Ag略高（83 GPa）.35从应力上比较四种孪晶纳米线不难看出，随着TBS的减小纳米线的应力极值明显增加. 但与Single比较发现，NW5、NW14和NW39的应力极值较大，而NW1的应力极值较小，说明引入孪晶对纳米线力学性质的影响（强化或弱化作用）与孪晶界密度密切相关. 需要注意的是，NW5在应力首次达到3.4 GPa后出现一短暂平台，而后继续上升至4.4 GPa，这一过程表现为应变硬化，在TBS为3.6 nm的Au纳米线拉伸过程中也表现出类似的现象.36

此外还比较了五种纳米线的塑性形变. 在图2中可以明显看出，四种孪晶纳米线的断裂应变都比单晶小，这种塑性降低是由孪晶界的塑性局部化导致的. 当引入的孪晶界较多时（NW39、NW14和NW5），纳米线应力显著上升但其塑性下降，因此可认为孪晶纳米线的应力提高是通过牺牲其塑性来实现的.16，31然而，这并不意味着孪晶纳米线的屈服应力越大其塑性就越差，NW39和NW14的最大应力和塑性都比NW5有所增强，与实验观察到的结果一致.21

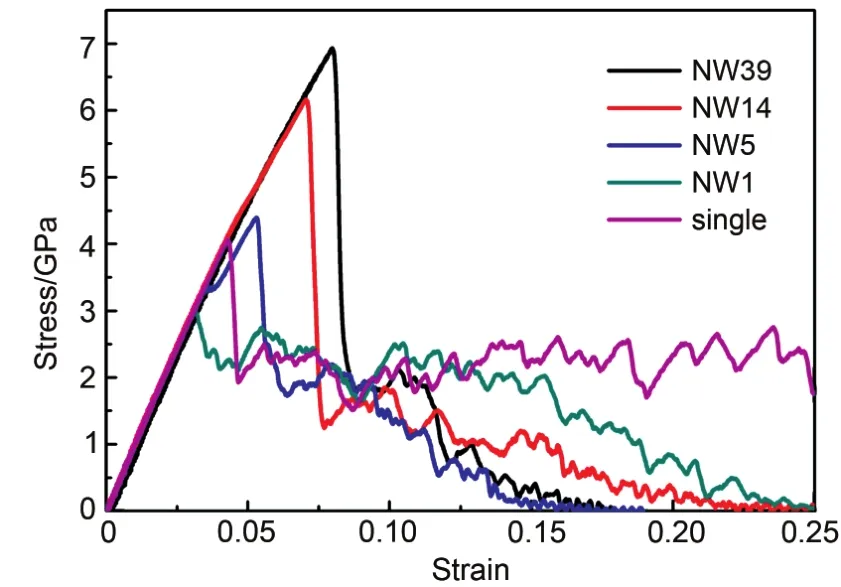
图2 不同孪晶界密度的Ag纳米线拉伸的应力应变曲线Fig.2 Stress-strain curves of Ag NWs with different TB densities

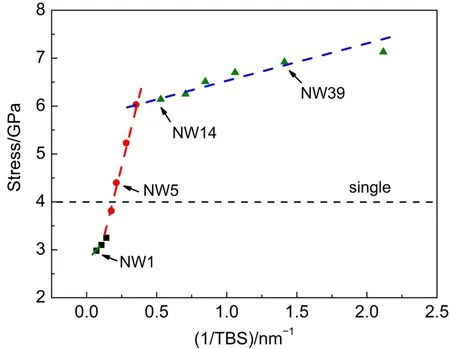
图3 不同孪晶界密度的Ag纳米线的应力极值和1/TBS的变化关系Fig.3 Evolution of ultimate stress as a function of 1/TBS in twinned Ag NWs with different TB densities

图3表明了纳米线应力极值和TBS的关系. 随着孪晶界密度变化可将应力极值的变化分情况讨论:当1/TBS小于0.2 nm-1时（方块部分），孪晶的最大应力都比单晶小，孪晶界对纳米线起到弱化作用，NW1即属于这种情况. 当1/TBS大于0.2 nm-1时，孪晶界对纳米线起到强化作用，而强化作用又因影响程度不同分为两种: 当1/TBS介于0.2和0.35 nm-1之间时（圆形部分），最大应力随TBS的减少迅速上升，与之前的模拟结果一致，孪晶内部可塞积位错的数量减小，因而位错穿过孪晶所需外加应力提高；19当1/TBS大于0.35 nm-1时（三角部分），最大应力随TBS的减少增幅变得平缓. 若将强化阶段进行整合，也可认为最大应力随1/TBS呈指数增长.

3.2 形变过程的微观结构分析

为了揭示TBS在孪晶纳米线中的塑性形变机理，对各类原子在形变过程中的变化情况进行了统计，如图4所示. 各类原子的变化数由当前原子数减去形变前的原子数计算得出，正数代表增加，负数代表减少，各类原子在形变过程中此消彼长，但无论原子类型如何转变，原子总数始终保持不变.

采用中心对称参数法研究纳米线的形变结构.当中心对称参数值pi介于0到0.4之间代表FCC原子，pi介于0.7到1.2之间代表HCP原子，pi大于1.2的原子代表其他原子，其中以表面原子为主.

在图4中，当纳米线处于弹性拉伸阶段时，其内部结构保持不变，各原子数不发生变化. 当拉伸到达纳米线的屈服点时，塑性形变即将发生，随着外力拉伸塑性形变不断增加，总体表现为FCC原子数下降，其他原子或HCP原子数增加. 由引入的孪晶界个数不同产生的塑性形变差异将在图4（a-d）中逐一说明.

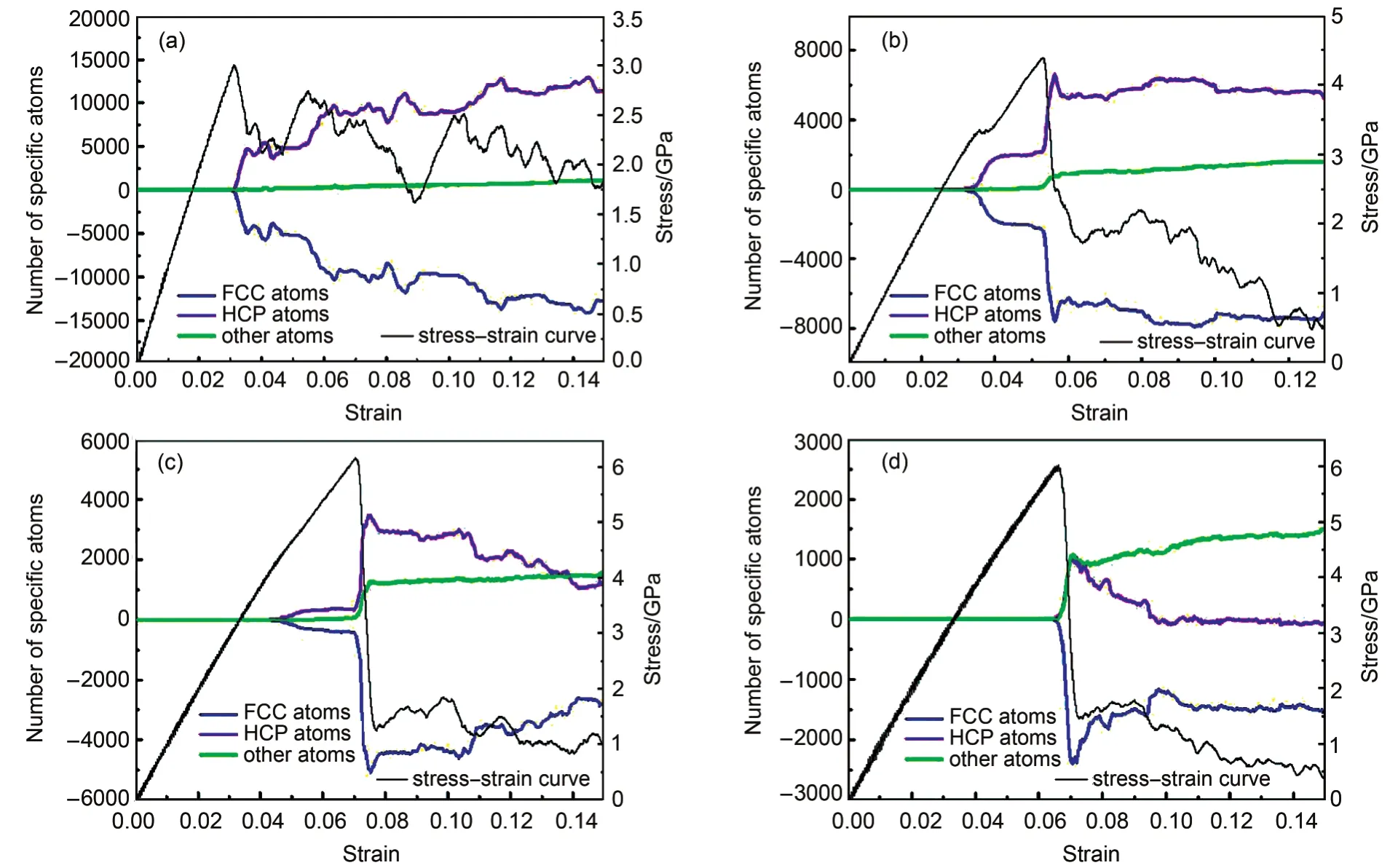
图4 各纳米线中不同种类原子个数和应力随应变变化图Fig.4 Variation number of different atoms and stress of each nanowire versus strain

图4（a）展示了NW1的FCC原子数呈震荡下降趋势. 在某些应变处，比如0.045和0.055之间以及0.09和0.102之间出现平台，FCC原子数保持不变，与应力应变曲线上的应力回复相对应，这是纳米线局部重结晶的结果； 图4（b）中FCC也有平台出现（集中在0.038和0.052之间），但图4（a）的差别在于，该平台紧随屈服点之后，反映的是纳米线的应变硬化阶段；随着引入孪晶界的个数增加，纳米线初始结构中的FCC原子不断减少，所以参与应变硬化的原子数相应减少（图4（c））； 当引入足够多的孪晶界时，应变硬化现象消失（图4（d）），形变模式发生转变.

在NW5、NW14和NW39中，孪晶界通过阻碍位错移动提高纳米线的强度. 当应力达到极值后迅速释放，FCC原子数急速下降，但随后的变化情况各不相同. 图4（a）中FCC原子数平稳缓慢下降； 图4（b）中FCC原子数基本保持不变； 图4（c）中FCC原子数在平稳后开始小幅度上升； 图4（d）中下降后的FCC迅速发生小幅度上升随后保持平稳状态. FCC原子数的增加表明在高密度孪晶纳米线的形变过程中存在去孪晶化现象.

四种孪晶纳米线在初始塑性形变过程中的HCP原子和其他原子的变化情况也各不相同. 图4（a）中的其他原子数基本保持不变，FCC原子数的减少主要体现在HCP原子的增加上，HCP曲线在震荡中逐步上升； 图4（b）中的其他原子数相较于图4（a）开始缓慢增加，在应变硬化阶段HCP迅速上升而后保持平稳； 图4（c）中的其他原子数在应变硬化结束后进一步增加，随后保持平稳，而HCP原子数在增加之后开始减少，进而出现低于其他原子数的情况. HCP的减少说明去孪晶化现象出现，塑性形变机理发生转变. 当孪晶界密度继续增加时，HCP原子比图4（c）中减少得更多，FCC原子主要向其他原子转化.

为了进一步探索不同孪晶密度下孪晶纳米线的初始塑性形变机理，我们对各纳米线在形变过程中的位图进行了分析. 图5为NW1的形变结构位图.对于有初始缺陷的晶体，位错将首先从晶体缺陷处萌生和发射. 由于模拟中使用自由边界条件，孪晶纳米线从自由表面和孪晶界交汇处开启定点位错（图5（a）），进而向内部展开位错成核和增殖（图5（b-d））. 拉伸形变过程中伴有不全位错的分解消失（图5（f，g））. 当积累到达一定程度时，位错打破孪晶界的限制，在邻近的孪晶片层内开始新的位错成核和增殖（图5（h-j））. 因此，在NW1的形变模式中孪晶界作为位错源，位错从自由表面和孪晶界交汇处启动成核.

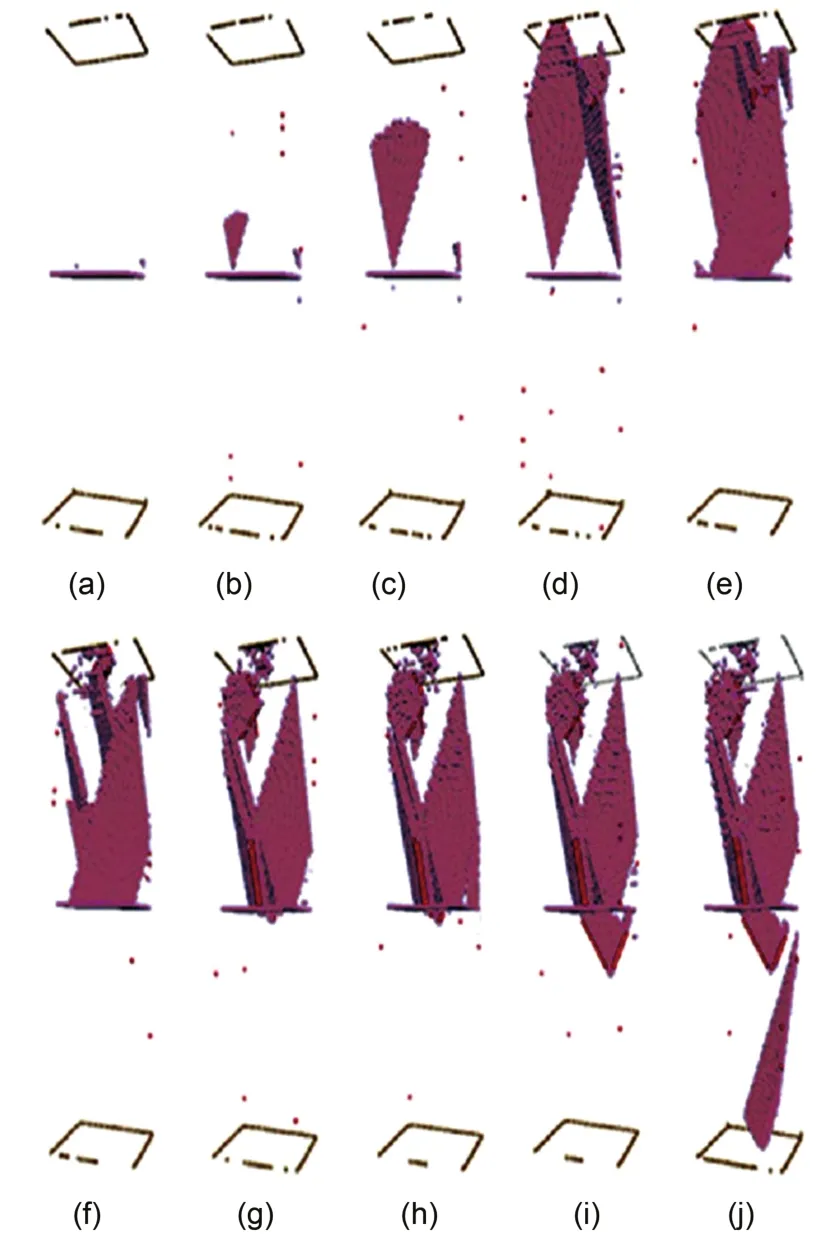
图5 NW1的拉伸形变结构位图Fig.5 Instantaneous deformation structures of NW1

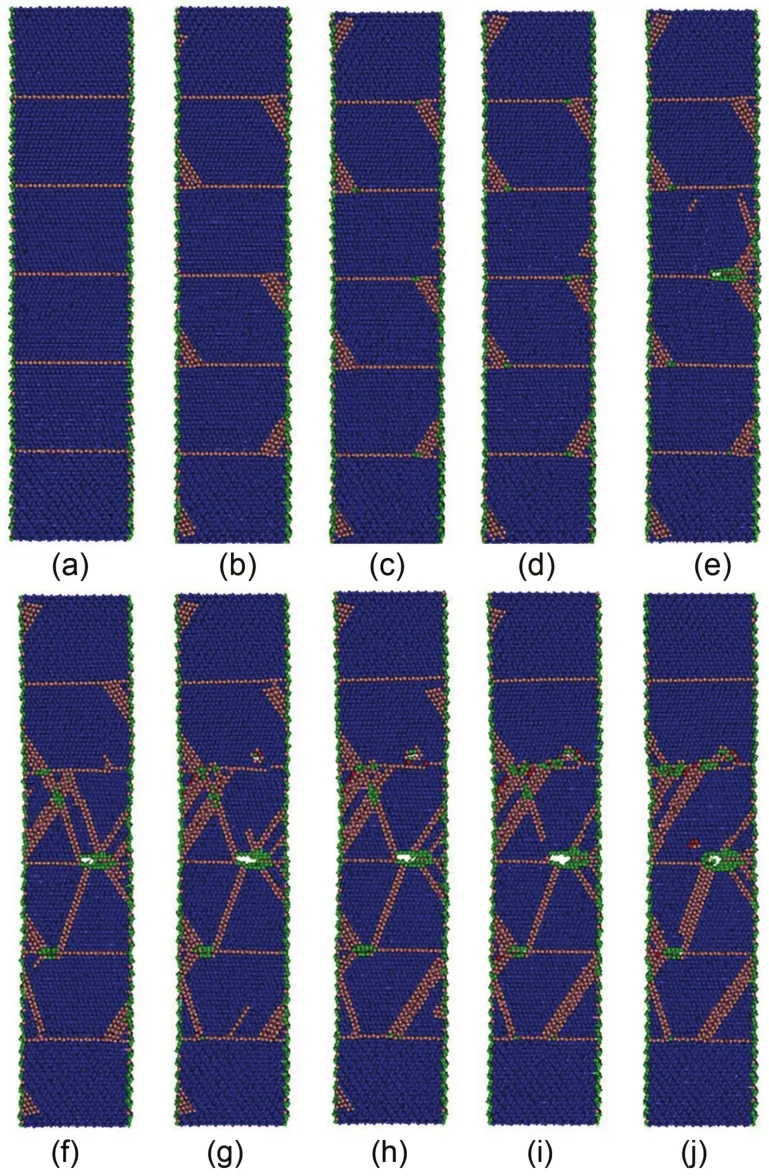
图6 NW5的拉伸形变结构位图Fig.6 Instantaneous deformation structures of NW5

图6为NW5在拉伸过程中的形变位图. 在塑性形变之前，NW5保持完美结构（图6（a））. 在应变硬化阶段，位错从表面发射受到孪晶界的阻挡（图6（b-d））. 在到达弹性极限时，孪晶界在改变位错方向的同时自身也遭到一定程度的破坏（图6（e））. 随着形变继续发生，有新的位错成核和增殖（图6（f））. 然而已经存在的位错趋于消失或是部分消失（图6（f-j）），这可能是因为位错之间或是位错与表面之间的相互作用导致的. 屈服应力之后，中间的孪晶面逐步遭到破坏. 所以1/TBS在0.2到0.5 nm-1之间的孪晶纳米线形变机理以孪晶界和位错相互作用为主导.

图7为NW14在拉伸过程中的形变位图. 在塑性形变之前，NW14保持完美的面心立方结构（图7（a））.在应变硬化阶段，位错从表面发射受到孪晶界的阻挡（图7（b-d））. 与图6不同的是，在到达弹性极限之前纳米线内部已产生新的位错成核和位错增殖（图7（e））. 孪晶界在阻挡位错时，位错和孪晶界的相互作用使得孪晶界发生迁移（图7（f-h））. 孪晶界的迁移导致颈缩区域的孪晶片层厚度增加，同时伴有不全位错消失. 随进一步拉伸，片层厚度显著增加以便为位错活动提供更多空间，位错不断移动和增殖直至打破孪晶界的限制. 孪晶界迁移使其储存位错的能力提高，从而容纳可观的塑性形变，提高纳米线的塑性. NW14的形变模式由孪晶界和位错相互作用向孪晶界迁移转变.

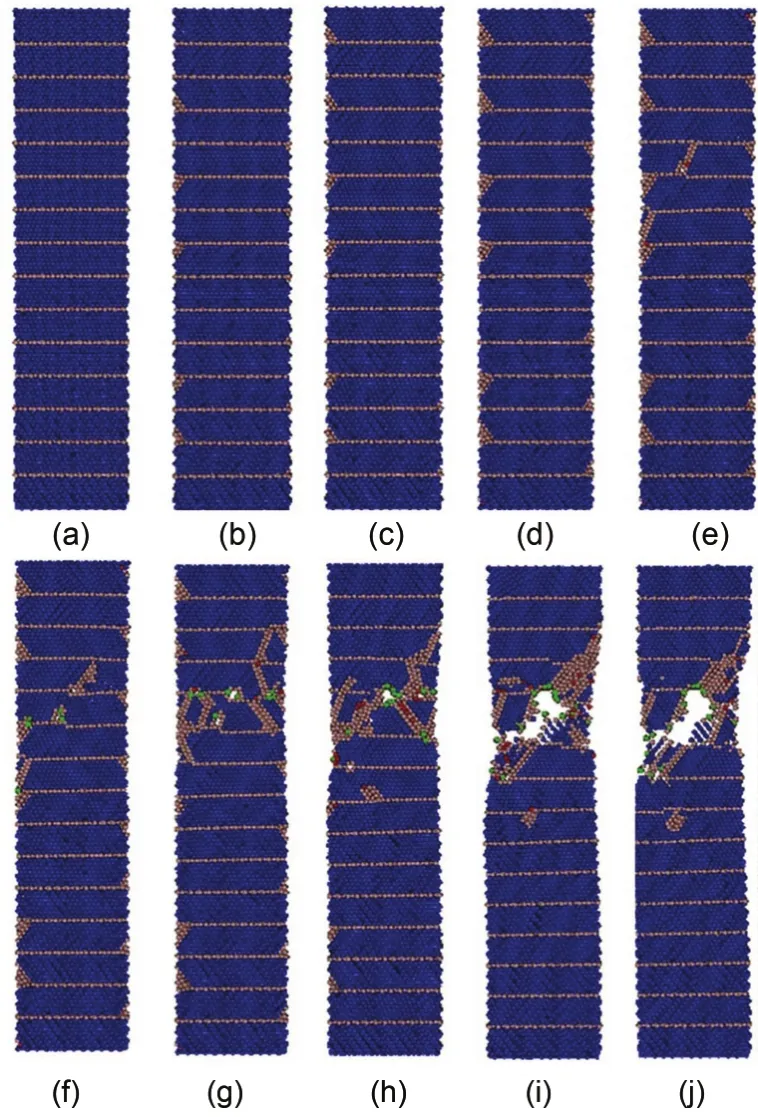
图7 NW14的拉伸形变结构位图Fig.7 Instantaneous deformation structures of NW14

图8为NW39在拉伸过程中的形变位图. 塑性形变开始发生时，初始位错从表面和晶界交汇处成核并且沿＜111＞方向移动和增殖. 在阻挡位错时，位错和孪晶界的相互作用使孪晶界发生迁移（图8（c-j）），孪晶片层厚度的增加为位错活动提供更多空间. 位错不断增殖穿过孪晶界形成剪切带，同时孪晶带在剪切方向受到了严重扭曲. 需要注意的是，NW39与NW5和NW14颈缩时的形变情况有显著不同，NW5和NW14断裂前的开口均在纳米线内部产生，随着位错增殖形成孔洞进而向四周蔓延； 而NW39的缺陷生成是在纳米线表面，随着拉伸向内部逐渐扩散. 剪切带在形成过程中表面附近出现局部混乱（图8（f-j）），这就解释了图4（d）中其他原子比HCP原子显著增加的原因.

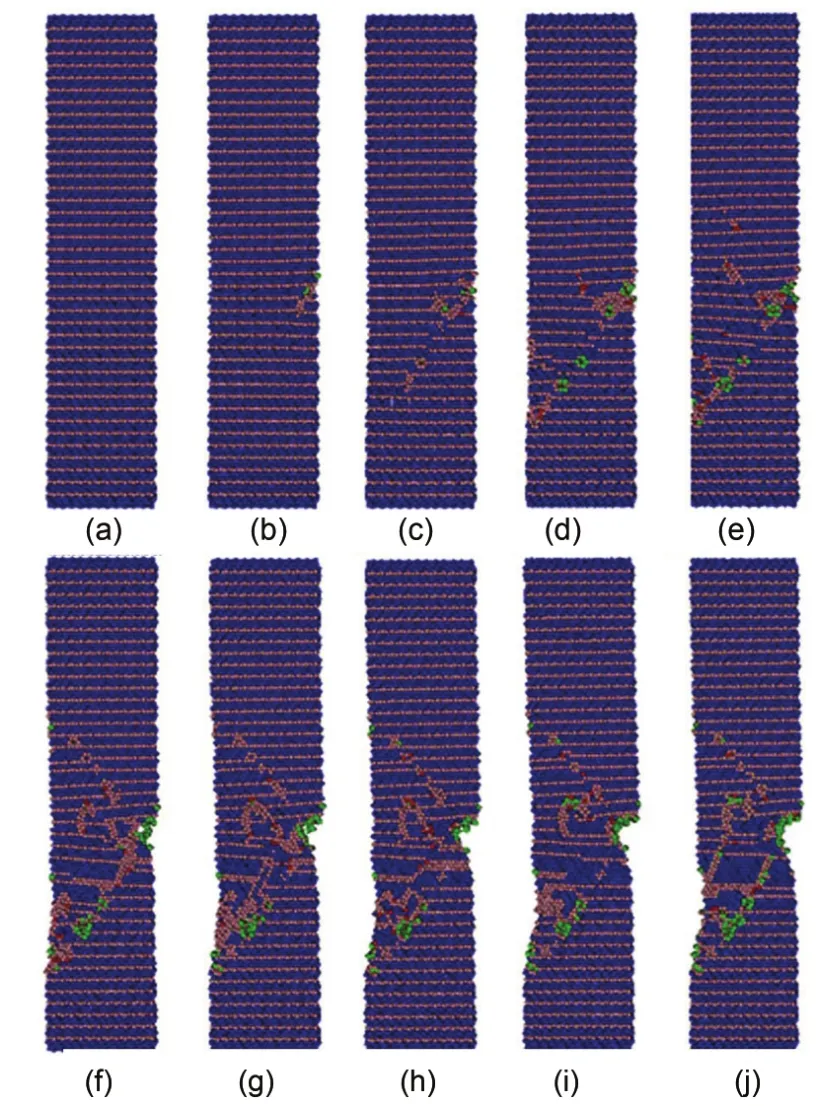
图8 NW39的拉伸形变结构位图Fig.8 Instantaneous deformation structures of NW39

此外还考察了温度对孪晶纳米线和单晶纳米线的影响. 如图9（a）所示，各温度下纳米线的应力极值随孪晶界密度升高呈现出类似指数的增长趋势.当温度从10 K上升至450 K时，原子动能增加，拉伸容易使原子偏离平衡位置，导致孪晶纳米线的强度减弱，并且由孪晶界密度不同引起的应力差值也相应减小. 图9（b）中展示了各孪晶纳米线与单晶纳米线的应力差值随温度的变化情况. 差值为正代表孪晶纳米线的强化作用，差值为负代表孪晶纳米线的弱化作用. 10 K下，由孪晶界密度不同引起的弱化作用和强化作用都很显著，两种作用效果均随温度升高而降低，在450 K时低密度孪晶界的弱化作用已经消失.

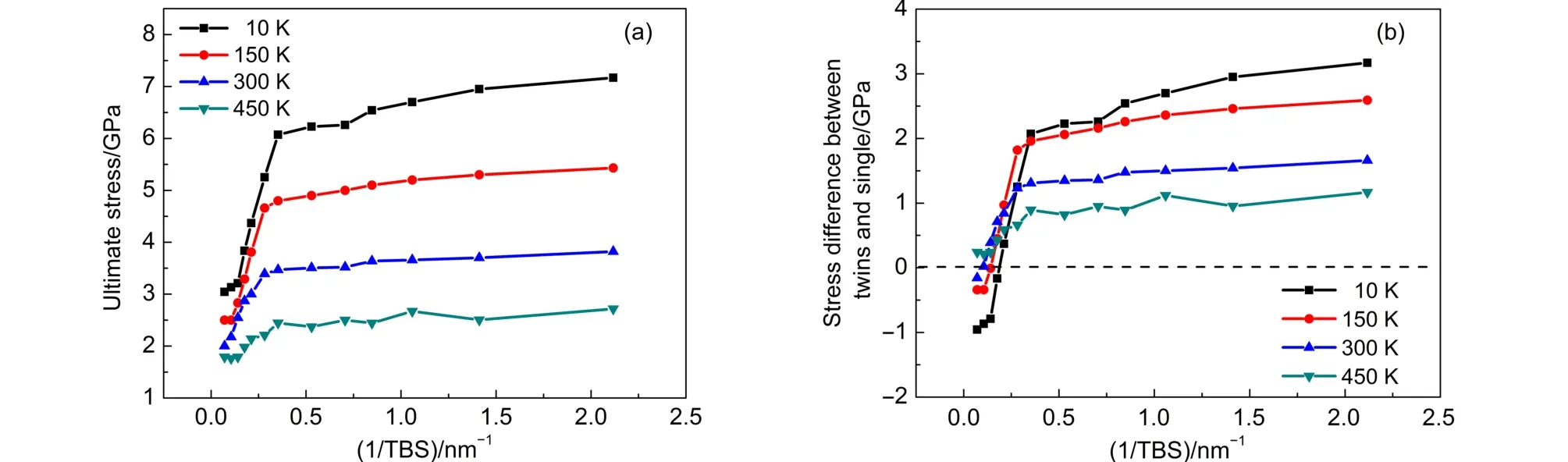
图9 应力极值随温度变化图Fig.9 Ultimate stress as a function of temperature

4 结 论

利用分子动力学方法研究了＜111＞晶向孪晶Ag纳米线在拉伸载荷下的形变行为，详细考察了孪晶界密度对纳米线的力学影响，揭示其内在的塑性形变机理. 由模拟结果可知，当1/TBS小于0.2 nm-1时，孪晶界作为位错源，表现为对纳米线的弱化作用； 当1/TBS大于0.2 nm-1时，孪晶界阻碍位错运动表现为强化作用. 其强化作用包括两种形式: 当1/TBS介于0.2到0.5 nm-1时，形变机理以孪晶界和位错相互作用为主，断裂开口从纳米线内部产生； 当1/TBS大于0.5 nm-1时，孪晶界发生迁移，位错越过孪晶界形成剪切带，表面原子无序进而导致纳米线的颈缩. 本文提出的孪晶纳米线的形变机理为构建高强度纳米线、避免纳米线的形变和失效奠定理论基础.

（1）Zhong，S.； Koch，T.； Wang，M.； Scherer，T.； Walheim，S.； Hahn，H.； Schimmel，T. Small 2009，5 （20），2265. doi: 10.1002/smll.v5:20

（2）Capolungo，L.； Spearot，D. E.； Cherkaoui，M.； McDowell，D. L.；Qu，J.； Jacob，K. I. J. Mech. Phys. Solids 2007，55 （11），2300. doi: 10.1016/j.jmps.2007.04.001

（3）Jin，Z. H.； Gumbsch，P.； Albe，K.； Ma，E.； Lu，K.； Gleiter，H.；Hahn，H. Acta Mater. 2008，56 （5），1126. doi: 10.1016/j.actamat.2007.11.020

（4）Lu，L.； Sui，M. L.； Lu，K. Science 2000，287 （5457），1463. doi: 10.1126/science.287.5457.1463

（5）Lu，L.； Shen，Y. F.； Chen，X. H.； Qian，L. H.； Lu，K. Science 2004，304 （5669），422. doi: 10.1126/science.1092905

（6）Lu，L.； Chen，X.； Huang，X.； Lu，K. Science 2009，323 （5914），607. doi: 10.1126/science.1167641

（7）Lu，K.； Lu，L.； Suresh，S. Science 2009，324 （5925），349. doi: 10.1126/science.1159610

（8）Shen，Y. F.； Lu，L.； Lu，Q. H.； Jin，Z. H.； Lu，K. Scr. Mater. 2005，52 （10），989. doi: 10.1016/j.scriptamat.2005.01.033

（9）Sangid，M. D.； Ezaz，T.； Sehitoglu，H.； Robertson，I. M. Acta Mater. 2011，59 （1），283. doi: 10.1016/j.actamat.2010.09.032

（10）Zhu，W.； Wang，H.； Yang，W. Acta Mater. 2012，60 （20），7112. doi: 10.1016/j.actamat.2012.09.018

（11）McDowell，M. T.； Leach，A. M.； Gaill，K. Nano Lett. 2008，8（11），3613. doi: 10.1021/nl801526c

（12）Guo，X.； Xia，Y. Z. Acta Mater. 2011，59 （6），2350. doi: 10.1016/j.actamat.2010.12.031

（13）Kulkarni，Y.； Asaro，R. J. Acta Mater. 2009，57 （16），4835. doi: 10.1016/j.actamat.2009.06.047

（14）Zhang，Y. F.； Huang，H. C.； Atluri，S. N. CMES-Comp. Model. Eng. Sci 2008，35 （3），215.

（15）Ding，F.； Li，H.； Wang，J. L.； Shen，W. F.； Wang，G. H. J. Phys. -Condes. Mat. 2002，14 （1），113. doi: 10.1088/0953-8984/14/1/310

（16）Cao，A. J.； Wei，Y. G. Phys. Rev. B 2006，74 （21），214108. doi: 10.1103/PhysRevB.74.214108

（17）Deng，C.； Sansoz，F. ACS Nano 2009，3 （10），3001. doi: 10.1021/nn900668p

（18）Deng，C.； Sansoz，F. Nano Lett. 2009，9 （4），1517. doi: 10.1021/nl803553b

（19）Deng，C.； Sansoz，F. Scr. Mater. 2010，63 （1），50. doi: 10.1016/j.scriptamat.2010.03.005

（20）Deng，C.； Sansoz，F. Appl. Phys. Lett. 2009，95 （9），091914. 10.1033/1.3222936

（21）Jang，D.； Li，X.； Gao，H.； Greer，J. R. Nat. Nanotechnol. 2012，7（9），594. doi: 10.1038/nnano.2012.116

（22）Sun，Q.； Yang，X. B.； Gao，Y. J.； Zhao，J. W. Acta Phys. -Chim. Sin. 2014，30 （11），2015. ［孙 倩，杨雄博，高亚军，赵健伟.物理化学学报，2014，30 （11），2015.］ doi: 10.3866/PKU. WHXB201409101

（23）Daw，M. S.； Baskes，M. I. Riv. Patol. Clin. 1983，50 （17），1285.

（24）Verlet，L.； Verlet，L. Phys. Rev. 1967，159 （1），98. doi: 10.1103/PhysRev.159.98

（25）Nose，S. J. Chem. Phys. 1984，81 （1），511. doi: 10.1063/1.447334

（26）Hoover，W. G. Phys. Rev. A 1985，31 （3），1695. doi: 10.1103/PhysRevA.31.1695

（27）Zhao，J. W.； Yin，X.； Liang，S.； Liu，Y. H.； Wang，D. X.； Deng，S. Y.； Hou，J. Chem. Res. Chin. Univ. 2008，24 （3），367. doi: 10.1016/S1005-9040（08）60077-X

（28）Gao，Y. J.； Wang，H. B.； Zhao，J. W.； Sun，C. Q.； Wang，F. Y. Comput. Mater. Sci. 2011，50 （10），3032. doi: 10.1016/j.commatsci.2011.05.023

（29）Sun，Y. L.； Sun，W.； Fu，Y. Q.； Wang，F. Y.； Gao，Y. J.； Zhao，J. W. Comput. Mater. Sci. 2013，79，63. doi: 10.1016/j.commatsci. 2013.06.004

（30）Liu，Y. H.； Zhao，J. W.； Wang，F. Y. Phys. Rev. B 2009，80 （11），115417. doi: 10.1103/PhysRevB.80.115417

（31）Wang，F. Y.； Gao，Y. J.； Zhu，T. M.； Zhao，J. W. Nanoscale Res. Lett. 2011，6，291. doi: 10.1186/1556-276X-6-291

（32）Gao，Y. J.； Fu，Y. Q.； Sun，W.； Sun，Y. L.； Wang，H. B.； Wang，F. Y.； Zhao，J. W. Comput. Mater. Sci. 2012，55，322. doi: 10.1016/j.commatsci.2011.11.005

（33）Gao，Y. J.； Wang，F. Y.； Zhu，T. M.； Zhao，J. W. Comput. Mater. Sci. 2010，49 （4），826. doi: 10.1016/j.commatsci.2010.06.031

（34）Wang，D. X.； Zhao，J. W.； Hu，S.； Yin，X.； Liang，S.； Liu，Y. H.；Deng，S. Y. Nano Lett. 2007，7 （5），1208. doi: 10.1021/nl0629512

（35）Wu，B.； Heidelberg，A.； Boland，J. J.； Sader，J. E.； Sun，X. M.；Li，Y. D. Nano Lett. 2006，6 （3），468. doi: 10.1021/nl052427f

（36）Deng，C.； Sansoz，F. Acta Mater. 2009，57 （20），6090. doi: 10.1016/j.actamat.2009.08.035

摘要： 设计合成了一种新型的基于咔唑单元的树枝状3,6-双噻吩咔唑衍生物（BTCPh）, 通过电化学聚合法制备出其均聚物及与3,4-乙烯二氧噻吩（EDOT）的共聚物薄膜. 利用电化学工作站-紫外可见光谱联用装置对两种聚合物的光谱电化学和电致变色（EC）性能进行表征. 测试结果表明, 均聚物（PBTCPh）薄膜在不同电压下可显示黄、绿、蓝、灰四种颜色； 而EDOT单元的引入使共聚物P（BTCPh-EDOT）进一步增加了掺杂态, 从而显示出更加丰富的五种颜色（橙、绿、棕绿、蓝、灰）. 此外, 两种聚合物薄膜均具有良好的光学对比度和快速的响应速度, 因而使其在智能窗及显示器方面展现了潜在的应用前景.

关键词： 电致变色； 咔唑； 噻吩； 树枝状； EDOT

中图分类号： O646

doi: 10.3866/PKU.WHXB201509062

Simulation of Tensile Deformation of Twin Silver Nanowires Based on Molecular Dynamics

SUN Yin-Lu GAO Ya-Jun SUN Qian ZHAO Jian-Wei*
（State Key Laboratory of Analytical Chemistry for Life Science，School of Chemistry and Chemical Engineering，Nanjing University，Nanjing 210023，P. R. China）

This study investigated the deformation behavior of ＜111＞ twin Ag nanowires with differing parallel twin boundary （TB） densities under tensile loading via molecular dynamics （MD） simulations. The effect of TB density on the ultimate stress of nanowires is discussed, and the plastic deformation mechanisms of nanowires are illustrated. The results show that, in contrast to a single crystalline nanowire with the same size, the introduction of the TB can strengthen or soften nanowires through individual deformation modes, which indicates that there exists a critical twin boundary space （TBS） （where the value of the critical 1/TBS is 0.2 nm-1）. Below 0.2 nm-1, softening occurs, whereby TBs become the source of dislocations. Above 0.2 nm-1, TBs impede dislocation movement, which results in a strengthening effect. The strengthening mechanisms are divided into two types. When 1/TBS ranges from 0.2 to 0.5 nm-1, the TB-dislocation interaction is the controlling factor. Fracture opening appears within the nanowires, and voids form, with dislocation multiplication, and then spread to the surrounding regions. When 1/TBS is greater than 0.5 nm-1, TBs migrate to accommodate dislocation activity. Dislocations increase and transfer across the TBs. Shear banding is activated during the process, which contributes to the necking of nanowires. The strengthening and weakening effects caused by differences in TB density decrease with increasing temperature.

Molecular dynamics； Ag nanowire； Twin boundary density； Tensile loading； Deformation

多色显示树枝状聚（3，6-双噻吩咔唑）及其共聚物的电化学和电致变色性能

边高峰1,2胡 彬3欧阳密1王萍静1吕晓静1,*戴玉玉1张 诚1,*

（1浙江工业大学化学工程学院，杭州 310014；2杭州师范大学有机硅化学及材料技术重点实验室，杭州 311121；3周口师范学院，稀土功能材料及应用重点实验室，河南 周口 466001）

July 24，2015； Revised: September 4，2015； Published on Web: September 6，2015.

. Email: zhaojw@nju.edu.cn； Tel: +86-25-83596523.

O641

10.3866/PKU.WHXB201509063

The project was supported by the National Natural Science Foundation of China （21273113，21121091）.

国家自然科学基金（21273113，21121091）资助项目