系杆拱桥的横向振动特性分析*

刘世忠

（兰州交通大学土木工程学院 兰州，730070）



系杆拱桥的横向振动特性分析
*

刘世忠

（兰州交通大学土木工程学院 兰州，730070）

依据能量原理，选取系杆拱桥横向基频阵型为正弦波，计算了系杆拱体系的横向振动应变能以及动能，利用Rayleigh法，得到了系杆拱横向振动的基频计算公式，基频公式物理概念明确，与有限元法相比具有计算简便、精度高等优点；根据平衡原理推导出吊杆“非保向力效应”矩阵，采用自编程序计算了吊杆“非保向力效应”对系杆拱自振特性的影响。结果表明：吊杆“非保向力效应”对系杆拱桥的低阶横向自振频率有较大影响，吊杆的“非保向力效应”可提高系杆拱桥的横向振动基频，对系杆拱的抗震设计具有参考价值。

系杆拱桥；能量原理；横向基频公式；非保向力效应单元

引 言

改革开放以来我国已经修建了许多钢管混凝土拱桥，我国也是世界上地震灾害频发的国家之一，已有研究成果显示［1-2］，系杆拱横向第一振型占其地震反应的主要部分，笔者提出的系杆拱横向第一自振频率计算公式相对于空间有限元建模计算简便易行，计算精度高，可满足系杆拱抗震计算要求。依据平衡原理推导了吊杆“非保向力效应”矩阵，利用自编程序计算了吊杆“非保向力效应”对系杆拱自振特性的影响。结果表明：吊杆的“非保向力效应”对系杆拱桥横向低阶自振频率的影响不能忽略，但对竖向基频和高阶振动频率的影响较小。

1 系杆拱桥横向振动的应变能

假定拱肋横向振动基频对应振型按正弦函数y =A sin（π·G/GS）曲线振动［3］，其中GS为拱的总长度，G为从左端沿拱轴线任一点的弧长。拱肋两端支座处由于系梁（拱座）的约束不但使得y=0，而且扭转也为零，拱肋横向弯曲转角为d y/d s；引起的系杆截面的弯曲转角为（d y/d s）cosα，α为拱肋与系杆连接处的夹角；系杆对拱脚的约束力矩为（2EI/L0）·（d y/d s）cosα，EI为系杆横向抗弯刚度，L0为跨度。

设拱肋发生一阶横向振型，其对应的弯曲应变能可按下式计算：

其中：Π为体系的总应变能；Π0为拱肋的弯曲应变能；ΠH为横撑的弯曲应变能；ΠX为斜撑的弯曲应变能；ΠR为系杆对拱脚约束而产生的转动应变能。

由振型函数得拱肋（两片）的弯曲应变能为

其中：EGIG为一片拱的横向弯曲刚度。

设拱肋在横撑（斜撑）节点由于横向弯曲引起的相对于初始状态的转角为β，β=d y/d s=y′，则由此引起的横撑与斜撑的杆端弯矩为MH与MX，表达式［］为

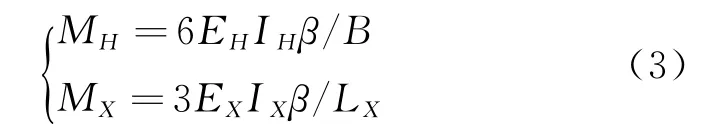
其中：EHIH，EXIX分别为横撑与斜撑的抗弯刚度；B为两拱肋横向宽度；LX为斜撑的长度；对于只设横撑没有斜撑的拱，MX=0。

一个横撑和斜撑的应变能分别为

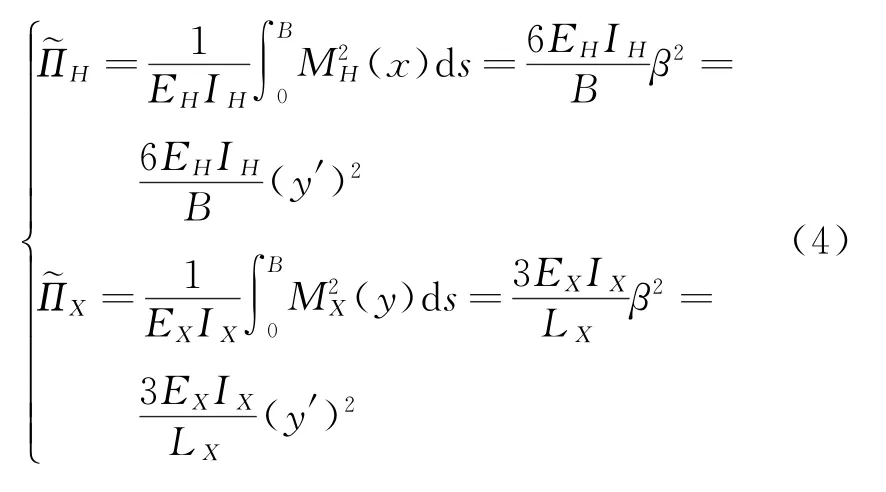
则全部横撑和斜撑的应变能为

系杆转动应变能为

设Δ为横撑在顺桥向的间距；系杆拱横向振动时的总应变能为

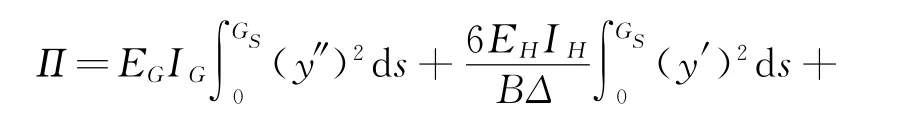
2 系杆拱桥横向振动的基频计算公式

设系杆拱横向振动的总应变能为Π，动能T为

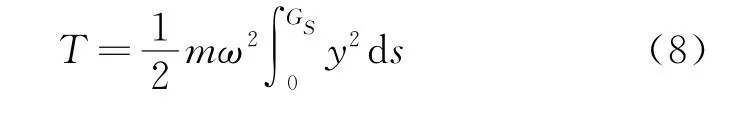
则由Rayleigh法知，体系的总应变能与动能相等，即得

将y=Asin（π·G/GS）代入式（9）计算整理得

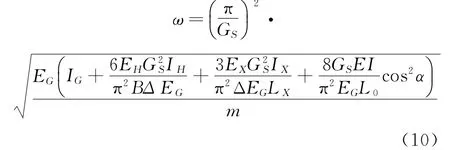
如横撑，拱肋斜撑和系杆为同一种材料，则E= EG=EH=EX，此时，可令

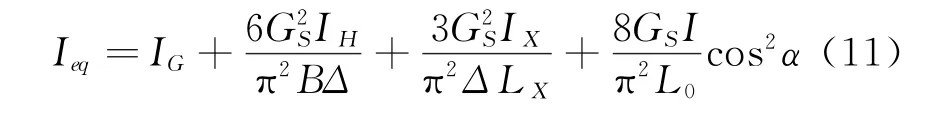
式（10）可简写为

3 算 例

3.1 下承式系杆拱桥［5］

某跨度为130m，桥宽25m的钢管混凝土系杆拱桥，系杆（纵梁）高为2.7m，宽1.6m的钢箱梁，吊杆采用50B级Φ100mm级钢拉棒，设计示意图见图1。

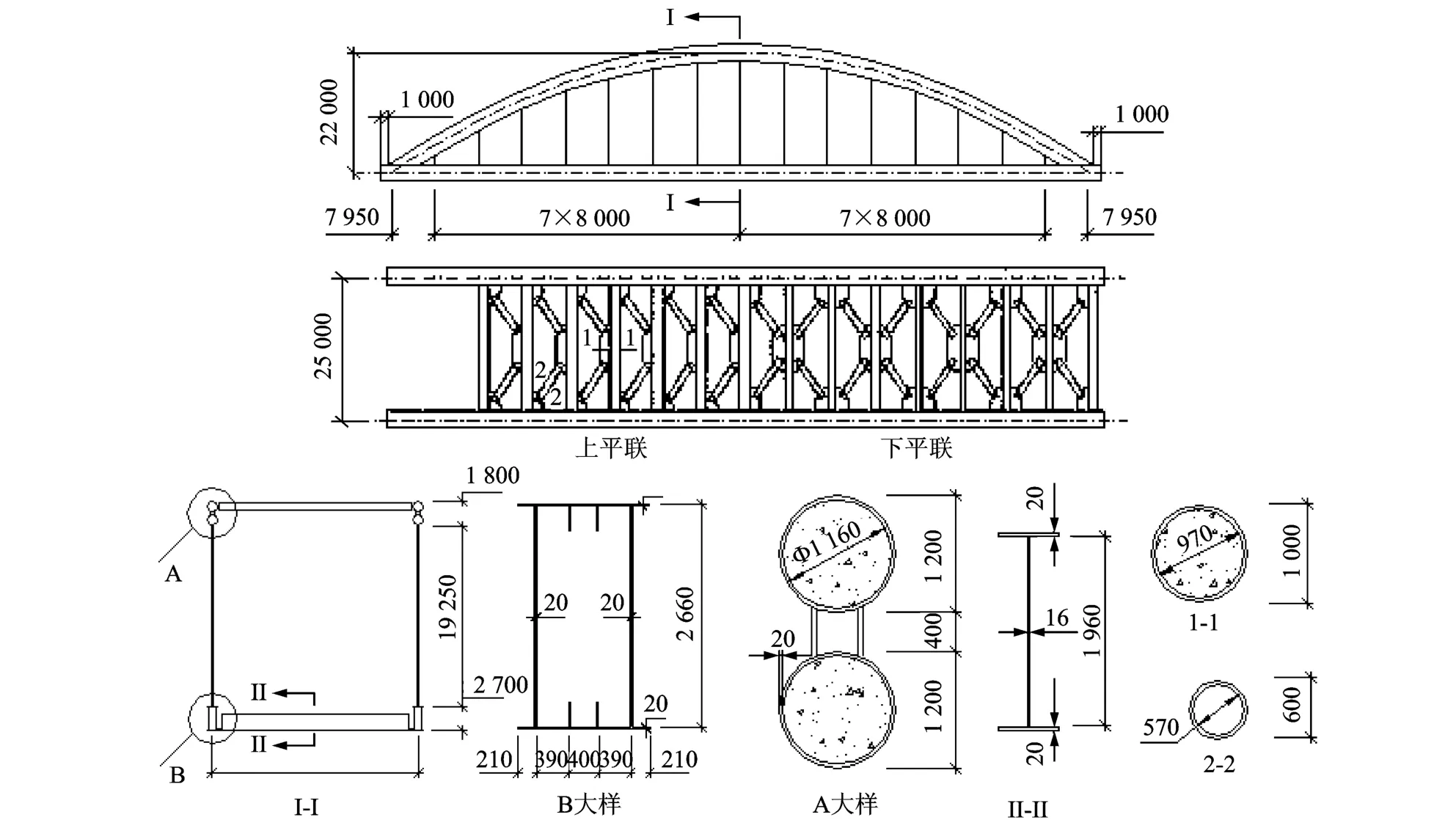
图1 设计示意图（单位：mm）Fig.1 Schematicdesign（Unit：mm）

系杆拱截面特性如表1所示。

表1　系杆拱截面特性Tab.1 Section properties of tied archbridge

拱肋弧长GS=137.366 m，跨度L0=130.00 m，节间长Δ=8 m，肋间斜撑长LX=14.84 m，拱肋与系杆夹角为α=0.605 6 rad，EG=E=2.1×108k Pa，EX=EH=3.3×107k Pa，单根拱肋的线质量m=8.758 k N·s2/m。

将以上参数代入式（10）、（11）可得

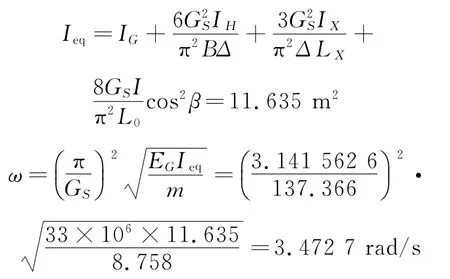
与三维有限元自振特性分析［4］所得横向一阶自振频率ωF=3.479 8 rad/s相比，相对误差小于1％，说明文中对系杆拱桥横向振动基频计算公式（11）具有相当高的精度。

3.2三连拱桥［3］

文献［3］给出的东岗黄河大桥为一三连拱铁路上承式拱桥（图2），采用空间动力分析SAP-V软件计算得到的横向振动基频及实测结果如表2所示（引自文献［3］表8-6）。第1，2频率代表两个边孔的横向振动，第3频率代表中孔的横向振动。

图2　东岗黄河大桥Fig.2 DONGGANG yellow river bridge

表2　三连拱桥横向自振频率Tab.2 Vibration frequency of triple arch bridge

桥梁基本参数为：拱轴弧长64 m，拱肋中心距2.6 m，单根拱肋横向平均惯性矩为0.100 5 m4，肋间横撑惯性矩为0.014 25 m4，节间长4.5 m，各构件材料弹性模量相同，为32.37×106k Pa，单根拱肋平均线质量m=7.34 k N·s2/m。由式（12）计算公式得

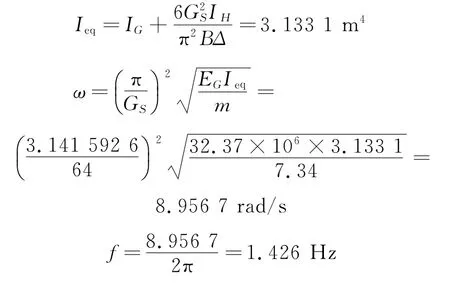
由推导的计算公式所得结果与有限元解第一孔横向振动频率的误差为3.06％，与实测值的误差仅为1.38％，完全满足工程计算精度需求。可见笔者依据能量原理推导建立的拱桥横向振动基频理论计算公式概念明确，计算简便，具有相当高的精度。

4 吊杆“非保向力效应”对系杆拱自振频率的影响

吊杆“非保向力效应”是指拱肋侧倾后，由于拱肋相对于桥面发生相对位移（ua-ub），吊杆发生倾斜，轴向拉力N对下弦桥面产生一个与侧倾方向相反的水平分力H，这个水平力H对拱肋相当于一个侧向水平弹性支撑作用效应，如图3所示。吊杆侧倾单元如图4所示。

如图3由平衡关系可得

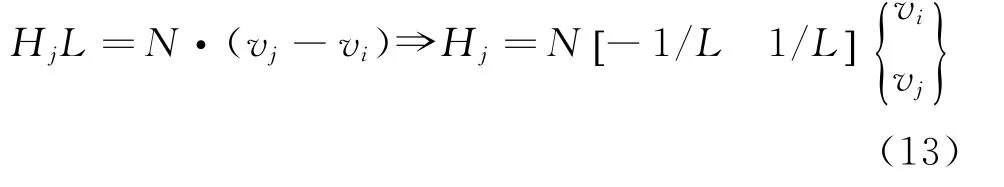
又因为Hj=-Hi，从而

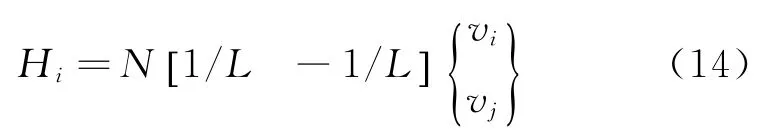
合并式（13），（14）可得

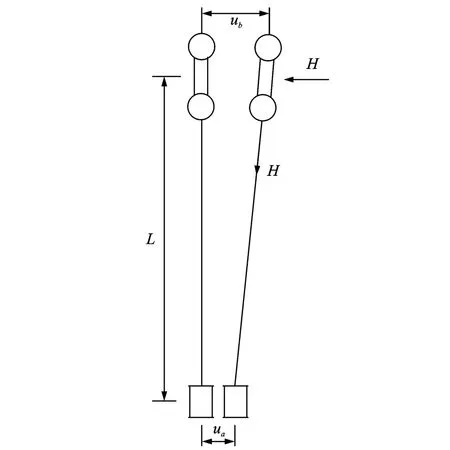
图3　“非保向力效应”图示Fig.3 Non conservative force effect graghic

图4　“非保向力效应”单元Fig.4 Element of non conservative force effect

令：

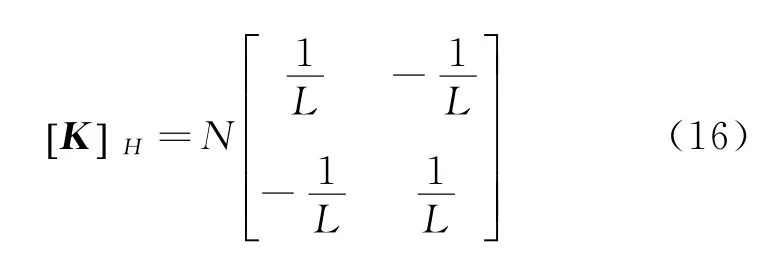
其中：［］KH称为吊杆侧倾刚度矩阵；N受拉为正，它反映出吊杆出拱平面“非保向力效应”的影响。

结构系统的无阻尼自由振动方程［6］为

频率方程为

式（18）采用修正的RITZ矢量直接迭加法［6-7］（MRVDS）的自编程序（PCFAP）计算，考虑和不考虑“非保向力效应”前6阶自振频率如表3所示，对应的振型如图5。

表3　自振频率比较表（ωi=2π/T i）Tab.3 Compare for vibration frequency（ωi=2π/Ti）

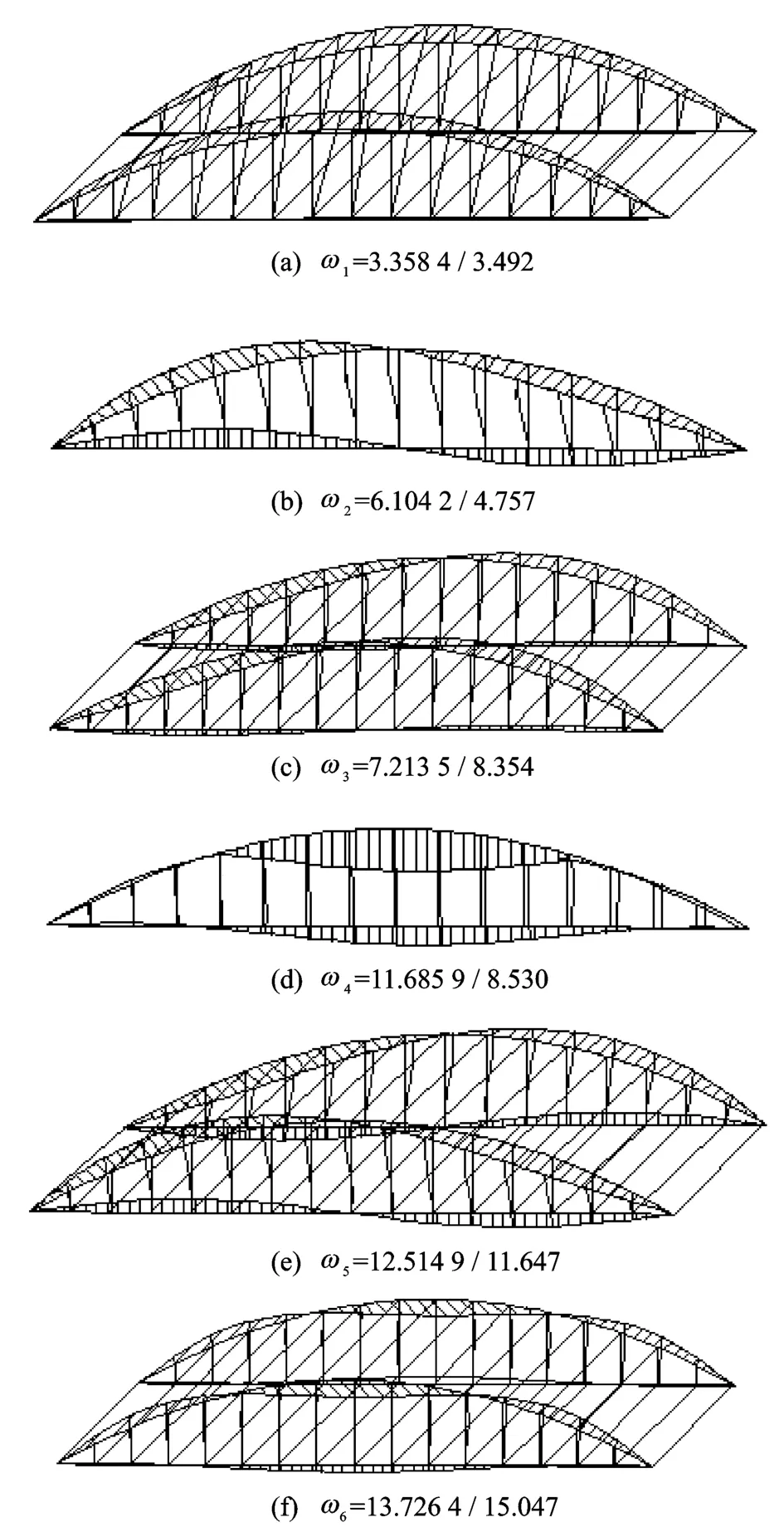
图5　系杆拱桥前6阶振型（单位：Hz）Fig.5 The six vibration type of the tied arch bridge（U-nit：Hz）

由表3和图5可知，吊杆的“非保向力效应”对系杆拱桥的横向低阶自振频率影响较大，吊杆的“非保向力效应”使得系杆拱桥的横向基频得以提高，使横向一阶和二阶自振频率分别提高9.57％和8.07％，而对高阶横向自振频率和竖向自振频率的影响较小。由图5可知，该系杆拱桥前6阶自振特性表现为：a.拱肋一阶横向振动；b.拱梁竖向一阶振动；c.拱肋横向二阶振动；d.拱梁竖向二阶振动；e.拱梁的竖向三阶振动；f.拱肋横向三阶振动。图5中自振频率物理意义为：不考虑“非保向力效应”ANSYS结果/考了“非保向力效应”的MRVDS法结果。

5 结束语

系杆拱桥的横向振动以及抗震问题［8］是桥梁工程师设计中必须认真研究的技术问题之一，这无不与基频特别是横向振动基频密切联系在一起，笔者为系杆拱桥的横向基频计算提供了简便的计算公式，探讨了吊杆“非保向力效应”对系杆拱桥自振特性的影响，笔者所得结论对系杆拱桥设计中的抗震计算与动力性能评估具有参考价值。

［1］ 范立础，胡世德，叶爱君.大跨度桥梁抗震设计［M］.北京：人民交通出版社，2001：35-45.

［2］ 李国豪.桥梁结构的稳定与振动［M］.北京：中国铁道出版社，1991：68-72.

［3］ 项海帆，刘光栋.拱结构的稳定与振动［M］.北京：人民交通出版社，1991：56-60.

［4］ 包世华.结构力学（上）［M］.3版.武汉：武汉理工大学出版社，2007：32-38.

［5］ 刘世忠，欧阳永金，沈波.钢管混凝土系杆拱桥的整体稳定性及自振特性分析［J］.甘肃科学学报，1994，6（1）：28-35. Liu Shizhong，Ouyang Yongjin，Shen Bo.An analysis of the structure stability and dynam IC behav 10R of a steel plpe arch bridge with vertical hangers［J］.Journal of Gansu Scieces，1994，6（1）：28-35.（in Chinese）

［6］ 吴鸿庆，任侠.结构有限元分析［M］.北京：中国铁道出版社，2000：89-96.

［7］ 任侠，吴鸿庆.用MRVDS方法求解振动特征值的若干问题［J］.铁道学报，1993，15（2）：93-100. Ren Xia，Wu Hongqing.On the convergence and rootmissing problem of the MRVDs method［J］.Journal of China Railway Society，1993，15（2）：93-100.（in Chinese）

［8］ 陈宝春.钢管混凝土拱桥设计与施工［M］.北京：人民交通出版社，1999：85-92.

U448.29

10.16450/j.cnki.issn.1004-6801.2015.02.001

刘世忠，男，1962年1月生，博士、教授博士生导师。主要研究方向为桥梁结构有限元分析，桥梁检测评估与加固。曾发表《大温差影响下刘家峡大桥基准索股的调整》（《桥梁建设》2014年第44卷第3期）等论文。

E-mail：Liusz2000@163.com

*国家自然科学基金资助项目（51368032）

2013-01-21；

2014-05-09