考虑变工况冲击的齿轮动态啮合力分析*

冯海生， 王黎钦， 郑德志， 赵小力， 戴光昊

（1.哈尔滨工业大学机电工程学院 哈尔滨，150001） （2.中国船舶重工集团公司第703研究所 哈尔滨，150036）



考虑变工况冲击的齿轮动态啮合力分析*

冯海生1， 王黎钦1， 郑德志1， 赵小力1， 戴光昊2

（1.哈尔滨工业大学机电工程学院 哈尔滨，150001） （2.中国船舶重工集团公司第703研究所 哈尔滨，150036）

为研究变工况冲击对齿轮传动系统动特性影响，文中基于弹塑性接触理论，给出一种可以考虑变工况冲击、啮入冲击、节点冲击的齿轮接触碰撞力参数预估算法，并结合多体动力学软件建立柔性齿轮传动系统动力学模型。该模型和算法可用于大接触变形和承受频繁冲击齿轮传动系统稳态和瞬态动特性分析。研究表明：与啮入冲击导致的稳态动态啮合力相比，变工况冲击引起的瞬态动态啮合力具有幅值大、冲击时间短等特点；在不同工况下，啮入冲击会引起不同周期的齿轮动态啮合力波动；滑动摩擦系数对齿轮切向摩擦力的节点冲击影响更大。研究结果对齿轮的接触碰撞力参数预估及全面认识齿轮传动系统瞬态动特性等研究具有积极的意义。

齿轮传动系统；变工况冲击；柔性体模型；接触碰撞；动态啮合力

引 言

齿轮系统作为传递动力和运动的机械装置而广泛应用于航空、航天、船舶等行业，其动特性研究也一直是国内外研究的热点。长期以来，对齿轮传动系统稳态动特性研究较多；而考虑节点冲击和变工况冲击的齿轮传动系统瞬态动特性研究较少。

文献［1］利用有限元法分析滑动摩擦和齿廓修形对齿轮副啮合特性的影响。结果表明滑动摩擦对齿轮啮入、啮出冲击影响不大，但会引起齿轮节点冲击。然而此文献并没有考虑变工况冲击所引起的齿轮系统瞬态动特性。文献［2-3］对齿轮瞬态相对转速变化而引起的齿轮瞬态啮合冲击做了有益的研究。文献［2］给出齿轮传动接触冲击的概念，并利用有限元分析冲击速度对冲击合力和冲击应力的影响。结果表明，冲击合力和冲击应力与冲击转速呈近似的线性增长关系。文献［3］在考虑电动机、柴油机变负载驱动的工况下分析高速重载齿轮传动系统瞬态动特性，结果发现齿轮瞬态动态啮合力远大于其稳态动态啮合力。

随着高性能计算机的广泛应用，使得利用多体动力学分析大柔度、强非线性的齿轮传动系统动特性成为现实［4］。文献［5］认为相对刚性体模型和有限元模型，利用模态缩减法的柔性多体齿轮传动系统模型能够提供更加合理的仿真效率和计算精度。当前，影响齿轮传动系统多体动力学模型计算效率和精度的主要因素是齿轮接触力参数和柔性体模态缩减法的优化，其中现有接触力参数的预估多涉及稳态接触力参数而对瞬态接触力参数涉及较少［6-7］。因而，研究考虑瞬态和稳态冲击作用的齿轮接触力参数预估对齿轮传动系统动特性分析和减振降噪机理都具有重要意义。

文中在系统分析变工况冲击、啮入冲击、节点冲击等典型齿轮啮合碰撞速度的基础上，结合弹塑性变形恢复系数提出一种适用范围更大的齿轮接触碰撞力参数预估算法。该算法适用于大接触变形、频繁变工况冲击下齿轮传动系统的瞬态和稳态动特性分析。并对某型船用斜齿轮传动系统的多啮合周期动特性进行不同工况下的对比分析，以确定变工况冲击、啮入冲击、节点冲击等齿轮冲击所引起齿轮动态啮合力的变化行为。经验证，文中所提接触碰撞力参数预估算法可应用于齿轮传动系统的瞬态和稳态动特性研究。

1 齿轮接触碰撞力的计算方法

齿轮接触碰撞力可由法向接触力和切向摩擦力合成得到，如式（1）所示：

其中：F为接触碰撞力；Fn为法向接触力；Ff为切向摩擦力。

1.1法向接触力Fn

由于齿轮啮合传动时不可避免地存在轮齿变形，而应用等效弹簧阻尼模型来表示齿轮法向接触力，如式（2）所示：

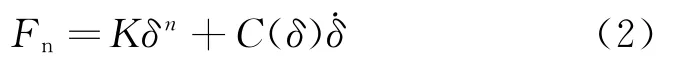
其中：K为等效接触刚度系数；δ为齿轮啮合点法向变形量；n为碰撞指数；C（δ）为接触阻尼多项式；.δ为齿轮法向变形速度。

1.1.1接触阻尼多项式C（δ）

C（δ）用来表征碰撞能量的损失。接触阻尼多项式采用文献［8］的非线性滞后阻尼模型，如式（3）所示：

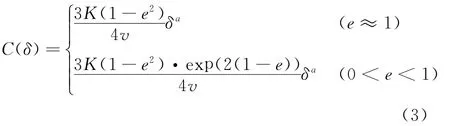
其中；v为齿轮啮合碰撞速度；e为碰撞恢复系数；a为非线性阻尼力指数。

1.1.2碰撞恢复系数e

e的实质是表示碰撞过程中的动能损失。为分析发生较大接触变形的齿轮传动系统动特性，文中采用文献［9］提出的改进碰撞恢复系数计算方法，如式（4）所示。该计算方法不仅包括弹性变形还引入弹塑性变形、有限塑性变形，同时还扩大已有碰撞恢复系数计算模型的应用范围。

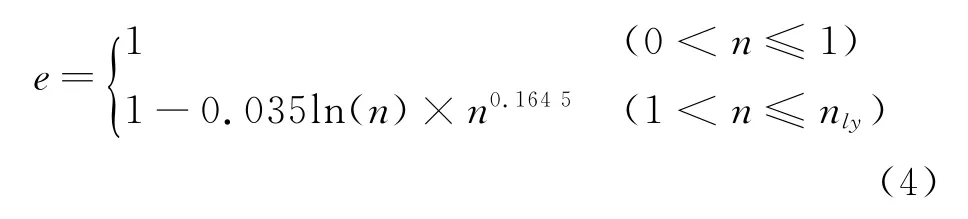
其中：n=v/vy；其他具体参数详见文献［9］。

1.1.3接触相对变形量δ

表征最大阻尼时的相对变形量。由Hertz接触理论可得弹塑性小变形接触碰撞中的变形量，即

由式（3）～（5）可知齿轮啮合碰撞速度v是接触阻尼、碰撞恢复系数、接触变形量的直接影响因素之一，也就是说，轮齿间的瞬态相对转速变化是导致齿轮传动系统动态啮合力变化的主要原因之一。大量研究表明，齿轮冲击作用是导致齿轮相对转速发生波动的最主要诱因之一。在齿轮传动系统的起动、加减速、突然停机和其他大范围工况波动等瞬态工况将产生较大接触碰撞力，文中将此瞬态区域的冲击力定义为变工况冲击力。同时，由于轮齿的受载变形和安装误差导致轮齿产生啮入、啮出冲击力。当齿轮传动考虑滑动摩擦时，因滑动速度方向在节点前后发生改变而导致节点冲击力的出现。

综上所述，通过计算变工况冲击、啮入冲击、节点冲击等典型齿轮冲击作用的齿轮啮合碰撞速度，则可求解建立包含瞬态冲击或稳态冲击齿轮动力学模型所需的齿轮接触碰撞力参数。

1.1.4齿轮啮合碰撞速度

（1）变工况冲击时的齿轮啮合碰撞速度

由于齿轮发生变工况冲击时其相应的齿轮啮合碰撞速度相差较大，则可将主、从动齿轮的变工况冲击假设为一个运动质量体与静止质量体的正心接触碰撞。变工况冲击速度如下所示：

其中：ω1，rl分别为主动齿轮的输入转速和分度圆半径。

（2）啮入、啮出冲击的齿轮啮合碰撞速度

在齿轮啮合过程中，由于存在轮齿误差和变形而导致主从动齿轮的基节不相等，导致齿轮的转速发生突变，进而引起啮入、啮出冲击。研究表明，啮入冲击对齿轮传动系统动特性的影响明显比啮出冲击大。因此文中仅研究啮入冲击，其啮入冲击速度vs如式（7）所示：

其中：αE1′为考虑轮齿误差和变形的实际啮合点压力角；r1′为实际啮合点E1′与主动齿轮中心点O1的连线O1E1′与两齿轮中心线之间的夹角。

（3）节点冲击的齿轮啮合碰撞速度

依据齿轮啮合原理，主、从动齿轮在齿面任意接触点H（除节点外）切线方向上的绝对速度不相同，则导致主、从动齿轮齿面的相对滑动。任意接触点H的相对滑动速度vt如下所示：

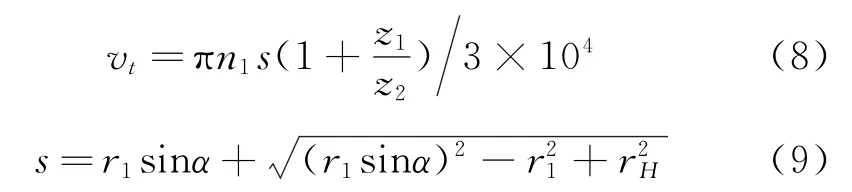
其中：s为任意啮合点H与节点在啮合线上的距离；rH为H点的主动齿轮啮合点半径。

通过式（6）～（8）可知，当齿轮啮合碰撞速度为变工况冲击速度时，则能够建立分析瞬态冲击和稳态冲击的齿轮传动系统动特性模型。

1.2切向摩擦力Ff

当考虑齿轮间的滑动摩擦时，则可采用库仑摩擦模型来表示切向摩擦力，如式（10）所示：

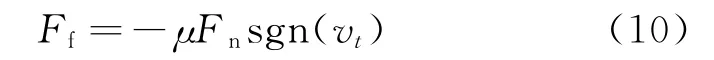
其中：μ为滑动摩擦系数；vt为啮合点的相对滑动速度。

一般工况下，齿轮的实际润滑状态为介于完全弹流润滑和边界润滑二者之间的混合弹流润滑，其滑动摩擦因数范围为0.04～0.10［10］。

2 齿轮传动系统的多体动力学模型

为研究考虑较大柔性变形、强非线性的齿轮传动系统动特性而基于ADAMS（Automatic dynamic analysis of mechanical systems，简称ADAMS）建立柔性多体齿轮传动系统的动力学模型。在ADAMS中采用Impact函数来计算法向接触力，如下式所示：

其中：δmax为接触碰撞中最大变形量；Cmax为最大接触阻尼；其他参数见式（2）。

由于软件所推荐参数并没有考虑到不同工况下齿轮传动的特殊性，所以ADAMS仿真计算中参数预估成为近年多体动力学研究的重点。但对大变形、变工况冲击的齿轮传动系统齿轮接触碰撞力参数预估研究较少，而文中在系统分析变工况冲击、啮入冲击、节点冲击等典型齿轮啮合碰撞速度的基础上，结合弹塑性变形恢复系数提出一种适用于大变形、变工况冲击的轮齿间接触碰撞力参数预估算法。考虑齿轮传动系统不同工况要求，根据式（2）-（9）则可计算式（11）所需参数的预估值以建立包含瞬态和稳态齿轮系统动特性分析模型。

综上所述，基于模态缩减法和ADAMS的柔性多体齿轮传动系统动力学模型建立及其动力学仿真分析的主要过程包括：建立三维实体模型；施加约束、负载；设置接触碰撞力参数；选择动力学方程求解方法等。

3 齿轮传动系统的仿真分析

将文献［11］提供的齿轮参数代入到文中算法所建的动力学模型中，其相应的动态啮合力结果对比如图1所示，文中的结果（图1（a））与文献结果基本一致，初步验证文中所提接触碰撞力参数预估算法正确。

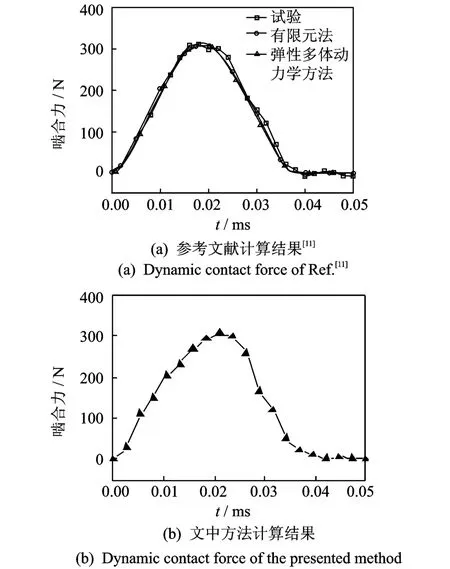
图1　结果对比图Fig.1 The diagram of comparison result

3.1仿真分析模型

以某船用减速器斜齿轮副的多啮合周期为研究对象，其几何参数如表1所示，材料均为20Cr Mn Mo。如第2节所述建立斜齿轮传动系统多体动力学模型（如图2）。同时，在主动齿轮上施加转速驱动，被动齿轮施加负载扭矩。动力学方程求解算法为变系数、变步长的预估校正算法。

表1　斜齿轮几何尺寸参数Tab.1 Structural parameters of helical gear

文中将分析此船用减速器两种极限工况下（如表2所示）的变工况冲击、啮入冲击、节点冲击对齿

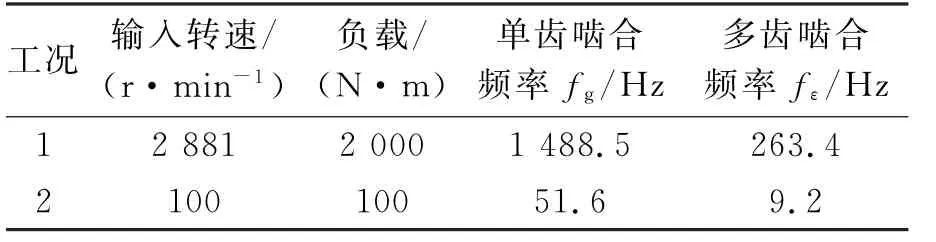
表2　齿轮传动系统动力学仿真参数Tab.2 Dynamic parameters of gear transmission

fg=1/Tg=（w1·z1）/60；fε=1/（ε·Tg），其中ε为重合度轮动态啮合力的影响。同时，为隔离高频振动噪声的影响，而对计算结果进行相应的Butterworth低通滤波降噪处理，其截至频率为5 k Hz。

图2　斜齿轮传动系统多体动力学模型Fig.2 Multi-body dynamics model of helical gear transmission

3.2瞬态和稳态区域的动态啮合力对比分析

如图3～5所示，在齿轮起动瞬间存在幅值较大的变工况冲击力，其幅值远大于稳态过程的啮入、啮出冲击力，并且冲击时间较短。而在稳态阶段则存在以静态法向啮合力值为中心的幅值较小、周期性变化的啮入啮出冲击力，而且其变化周期随着输入工况的不同而有所变化。如图4所示，工况1的稳态区域的啮入啮出冲击力变化周期为单齿完整啮入、啮出的多齿啮合周期Tε。如图5所示，在工况2的啮入啮出冲击力变化周期则主要为单齿啮合周期即Tg。如表3所示，稳态工况的动态啮合力均方差值与静态法向啮合力基本相同，表明基于文中模型的仿真结果是有效性。以上齿轮瞬态啮合力分析结果较已有研究［2-3］更加适合描述齿轮多周期啮合过程的动特性。

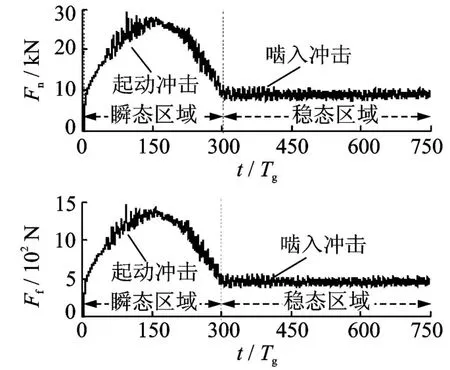
图3　工况1的法向动态接触力及摩擦力时域图Fig.3 The diagram of dynamic normal force and friction at case 1

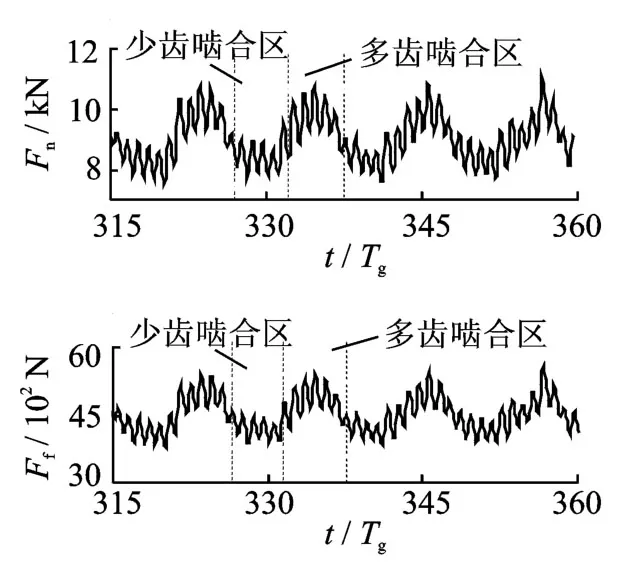
图4　工况1的法向动态接触力及摩擦力时域局部图Fig.4 The partial enlarged diagram of dynamic normal force and friction at case 1

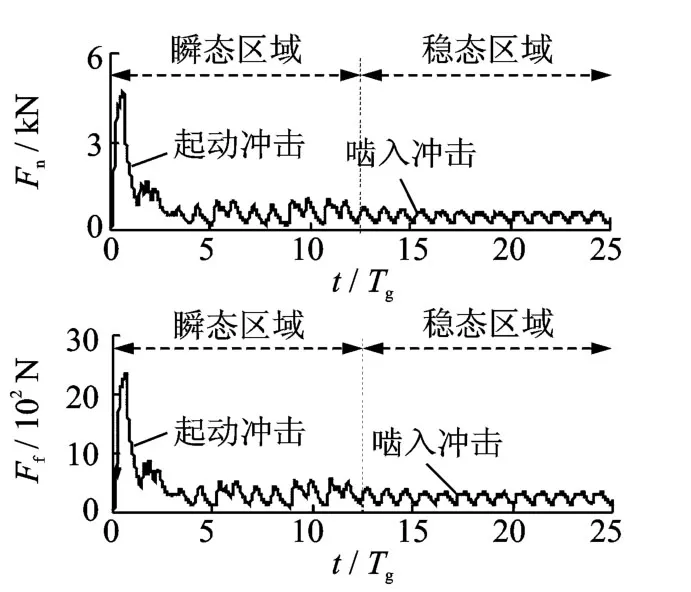
图5　工况2的法向动态接触力及摩擦力时域图Fig.5 The diagram of dynamic normal force and friction at case 2

表3　不同工况下动态啮合力的波动Tab.3 Fluctuation of dynamic meshing force at different cases N

结合表3和图3～5可知，工况2的变工况冲击力、啮入冲击力波动幅度大于工况1的变工况冲击力及啮入冲击力波动幅度，其中工况2的变工况冲击力的衰减幅度都大于工况1的相应衰减幅度。这是由于随着齿轮传递载荷增大，齿轮的接触变形增加、接触阻尼所吸收冲击能量变多，从而降低工况1的变工况冲击力及啮入冲击力波动幅度和衰减幅度。

3.3切向摩擦力分析

由式（10）可知，齿轮切向摩擦力与法向接触力的变化趋势同步、幅值成比例（如图3～5）。图3～5中的法向接触力、切向摩擦力为其各分力平方和的根，故图3～5中的法向接触力、切向摩擦力均为正值。由图6～7可知，齿轮相对滑动速度方向发生周期性（Tg）改变时，摩擦力的方向也发生相同周期的改变；同时由式（10）可知滑动速度和摩擦力的方向变化相反。

3.4不同滑动摩擦系数下的节点冲击分析

鉴于齿轮啮合位置不同时轮齿间的滑动摩擦系数不同，文中选择两组混合润滑状态下极限滑动摩擦系数（μ=0.05，μ=0.1）分析其对齿轮动态啮合的影响。

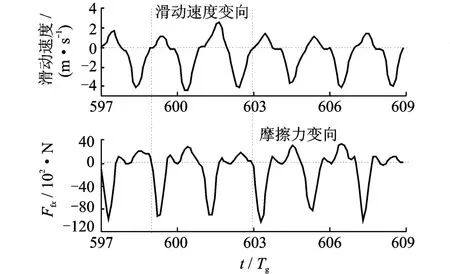
图6　工况1的摩擦力x向分量的时域图Fig.6 The diagram of x-component friction at case 1

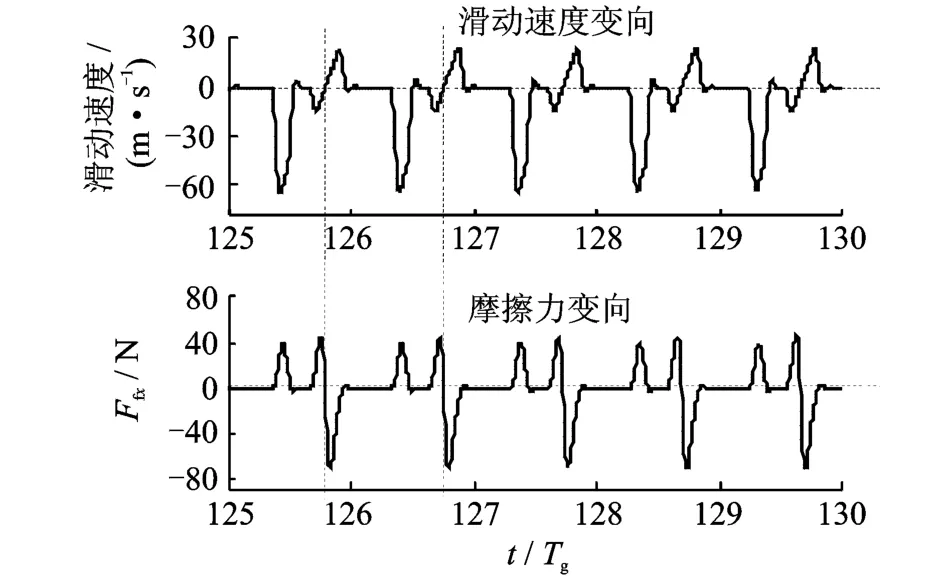
图7　工况2的摩擦力x向分量的时域图Fig.7 The diagram of x-component friction at case 2

如图8～11和表4所示，当轮齿间滑动摩擦系数增加时，不同工况下齿轮摩擦力的节点冲击幅值增加60％以上，而法向动态啮合力只有在工况1下有一定的波动，在工况2下几乎不变。由此可见滑动摩擦系数对工况1的齿轮动态啮合力影响较大。

图8　工况1的不同摩擦系数法向动态接触力x向分量时域图Fig.8 The diagram of dynamic normal force with different friction factor at case 1

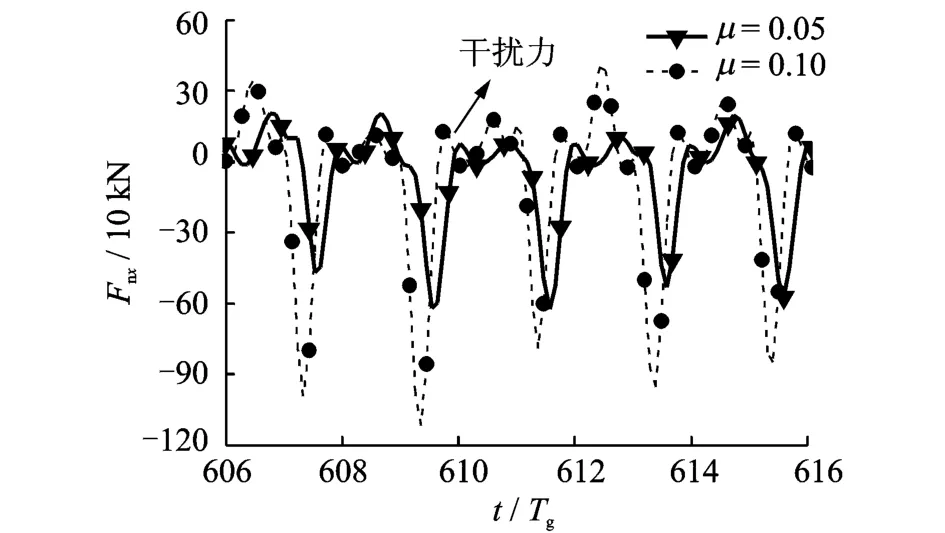
图9　工况1的不同摩擦系数切向摩擦力x向分量时域图Fig.9 The diagram of friction with different friction factor at case 1

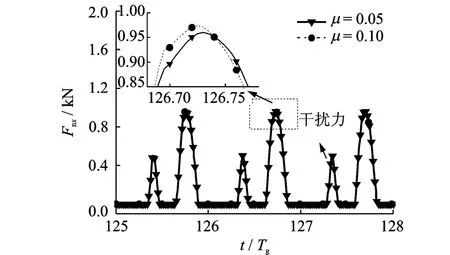
图10　工况2的不同摩擦系数下法向动态接触力x向分量时域图Fig.10 The diagram of dynamic normal force with different friction factor at case 2

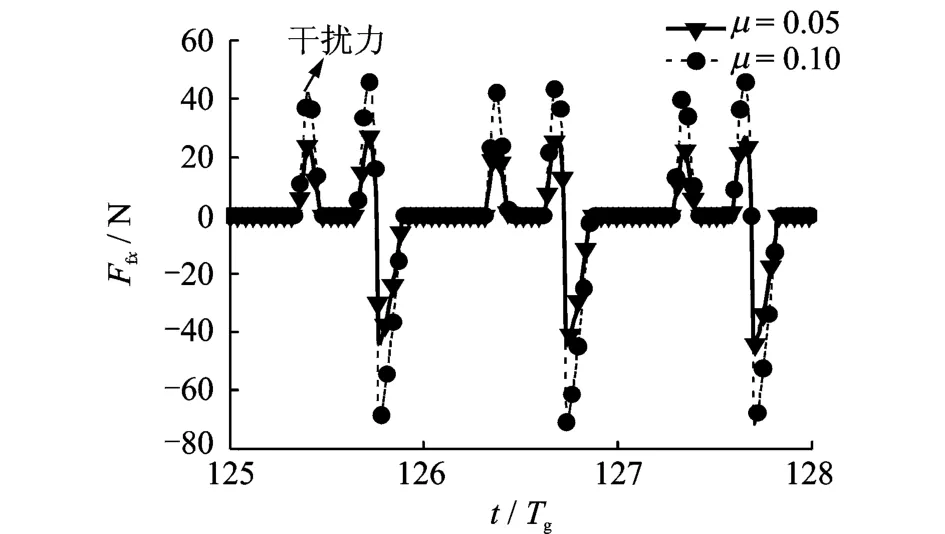
图11　工况2不同摩擦系数下切向摩擦力x向分量时域图Fig.11 The diagram of friction with different friction factor at case 2

表4　不同工况和摩擦系数下动态啮合力的波动Tab.4 Fluctuation of dynamic meshing force at different cases and friction factors N

与工况1相比，存在于法向接触力和切向摩擦中的干扰力在工况2时更加明显。这是由于工况1的载荷远大于工况2的载荷，所以相同的干扰力在大载荷工况下就不明显。针对干扰力产生的原因，将会在后续工作中研究。

4 结 论

1）针对齿轮动态啮合传动问题，给出一种考虑齿轮变工况冲击、啮入冲击、节点冲击的齿轮接触碰撞力参数预估算法，并结合多体动力学软件建立柔性多体齿轮传动系统动力学模型。该模型和参数预估算法适用于大接触变形和承受频繁冲击力的齿轮传动系统稳态和瞬态动特性分析。

2）相对啮入冲击和节点冲击，变工况冲击所引起的瞬态齿轮动态啮合力具有幅值大、冲击作用时间短等特点；啮入冲击引起的稳态齿轮动态啮合力具有周期性振动的特点，其中在转速较高、载荷较大工况下呈现多齿啮合周期（Tε）波动特征，而在低转速轻载荷工况下则表现为单齿啮合周期（Tg）波动。

3）低转速轻载荷工况下变工况冲击力、啮入冲击力的波动幅度大于转速较高、载荷较大工况下变工况冲击力、啮入冲击力的波动幅度。

4）由于滑动摩擦系数的增加，将导致齿轮切向摩擦力的节点冲击剧烈波动；而对齿轮法向接触力的节点冲击影响较小。

［1］ 吴勇军，王建军.一种考虑齿轮副连续啮合过程的接触有限元动力学分析方法［J］.航空动力学报，2013，28（5）：1192-1200. Wu Yongjun，Wang Jianjun.A contact finite element method for dynamic analysis of continuous engaged gear pairs［J］.Journal of Aerospace Power，2013，28（5）：1192-1200.（in Chinese）

［2］ 唐进元，周炜，陈思雨.齿轮传动啮合接触冲击分析［J］.机械工程学报，2011，47（7）：22-30. Tang Jinyuan，Zhou Wei，Chen Siyu.Contact-impact analysis of gear transmission system［J］.Journal of Mechanical Engineering，2011，47（7）：22-30.（in Chinese）

［3］ Khabou M T，Bouchaala N，Chaari F，et al.Study of a spur gear dynamic behavior in transient regime［J］. Mechanical Systems and Signal Processing，2011，25（8）：3089-3101.

［4］ 王 炎，马吉胜，郑海起，等.含柔性转子的齿轮-轴承系统动态特性分析［J］.振动、测试与诊断，2012，32（1）：495-499. Wang Yan，Ma Jisheng，Zheng Haiqi，et al.Dynamic characteristics analysis of gear-bearing system with flexible Rotor［J］.Journal of Vibration，Measurement &Diagnosis，2012，32（1），495-499.（in Chinese）

［5］ Ebrahimi S，Eberhard P.Rigid-elastic modeling of meshing gear wheels in multibody systems［J］.Multibody System Dynamics，2006，16（1）：55-71.

［6］ Seifried R，Schiehlen W，Eberhard P.The role of the coefficient of restitution on impact problems inmultibody dynamics［J］.Proceedings of the Institution of Mechanical Engineers，Part K：Journal of Multi-body Dynamics，2010，224（3）：224-279.

［7］ Tamarozzi T，Ziegler P，Eberhard P，et al.Static modes switching in gear contact simulation［J］.Mechanism and Machine Theory，2013，63：89-106.

［8］ 秦志英，陆启韶.基于恢复系数的碰撞过程模型分析［J］.动力学与控制学报，2006，4（12）：294-298. Qin Zhiying，Lu Qishao.Analysis of impact process model based on restitution coefficient［J］.Journal of Dynamics and Control，2006，4（12）：294-298.（in Chinese）

［9］ Feng Haisheng，Wang Liqin，Zheng Dezhi，et al.A-nalysis on dynamic contact force in high power density gear transmission based on flexible model［J］.Applied Mechanics and Materials，2013，328：547-551.

［10］Xu Hai，Kahraman A，Anderson N.Development of a generalized mechanical efficiency prediction methodology for gear pairs［R］.The Ohio State University，Department of Mechanical Engineering，2005：650.

［11］Ziegler P，Eberhard P.Simulative and experimental investigation of impacts on gear wheels［J］.Computer Methods Applied Mechanics and Engineering，2008，197（51），4653-4662.

TH132.41

10.16450/j.cnki.issn.1004-6801.2015.02.001

冯海生，男，1983年1月生，博士生。主要研究方向为高速齿轮传动系统动态特性及振动特性分析。曾发表《Transient dynamic analysis of high power density gear transmission》.《Proceedings of the Institution of Mechanical Engineers，Part J：Journal of Engineering Tribology》，2014，Vol.228，No.12）等论文。

E-mail：fenghaisheng01@163.com

*国家重点基础研究发展计划（973计划）资助项目（2013CB632305）；国家自然科学基金资助项目（51005050）；“十一五”国家传动基础资助项目

2013-10-16；

2013-12-20