重视基本活动经验 培养学生合情推理

钱长国

摘 要：基本活动经验是指学生的已有知识经验和生活经验。小学数学教学中教师要从学生的基本活动经验入手，创设情境，让学生通过观察、猜想、验证、归纳、类比、联想等方法，培养学生的合情推理能力。

关键词：基本活动经验；合情推理

中图分类号：G623.5 文献标识码：A 文章编号：1992-7711（2015）18-073-2

《小学数学课程标准（实验稿）》在课程的具体目标中指出：“培养和发展学生的合情推理能力。”合情推理最早是美籍数学家波利亚在30年代提出的概念，它是指“观察、归纳、类比、实验、猜测、矫正和调控等日常生活中积累的知识、经验，经过非演绎（非完全演绎）的思维而得到的合乎情理、理想化的一种推理方法。

波利亚说：“有效地应用合情推理是一种实际技能”。在小学数学教学中，教师要从学生的基本活动经验入手，培养学生的合情推理能力。

一、从学生生活经验入手，沟通算理联想推理

苏教版教材第7册中教学乘除混合运算时，有这样一道题，让学生计算56÷4÷7与56÷（4×7）的结果进行比较。教师让学生先猜想，然后通过计算得出：56÷4÷7=2，56÷（4×7）=56÷28=2。所以推理出56÷4÷7=56÷（4×7）。教学到此程度，不少教师都会让学生记住：在三个数连除算式中可以把后两个数用小括号括起来，括号里除号变乘号。它们的结果是一样的。事实上，我们可以根据学生已有的知识经验和生活经验进一步帮助学生理清算理，明了意义，更有助于学生理解、记忆。教师可以通过编生活中的应用题来理解算理。如：学校为了倡导足球文化，把56只足球平均分给三至六年级4个年级，每个年级7个班，平均每班分得足球多少只？学生有两种列式理由，一是根据数量关系式先求出平均每个年级分得足球多少只？（56÷4），再求平均每班分得足球多少只？（56÷4÷7）。第二种求法是先求出三至六年级共有几个班？（4×7），再求平均每班分得足球多少只？56÷（4×7）。最后让学生比较算理，思考所求问题，进一步得出：56÷4÷7与56÷（4×7）都是求平均每班分得足球多少只，它们是相等的。

二、借助线段图让学生观察，直观推理

小学数学教学中，巧妙借助线段图教学，可以化难为易，变抽象为具体，可以有效地帮助学生合情推理。

如：“学生问老师多少岁，老师说：‘当我像你这么大时，你刚3岁。当你像我这么大时，我已经39岁。那么，老师今年多少岁？”

这个问题，如果不借助线段图来直观观察，多数学生很难理解题目中隐藏的隐蔽条件，从而很难去推理。如果用线段图来表示，便于学生在头脑中形成正确的表征。

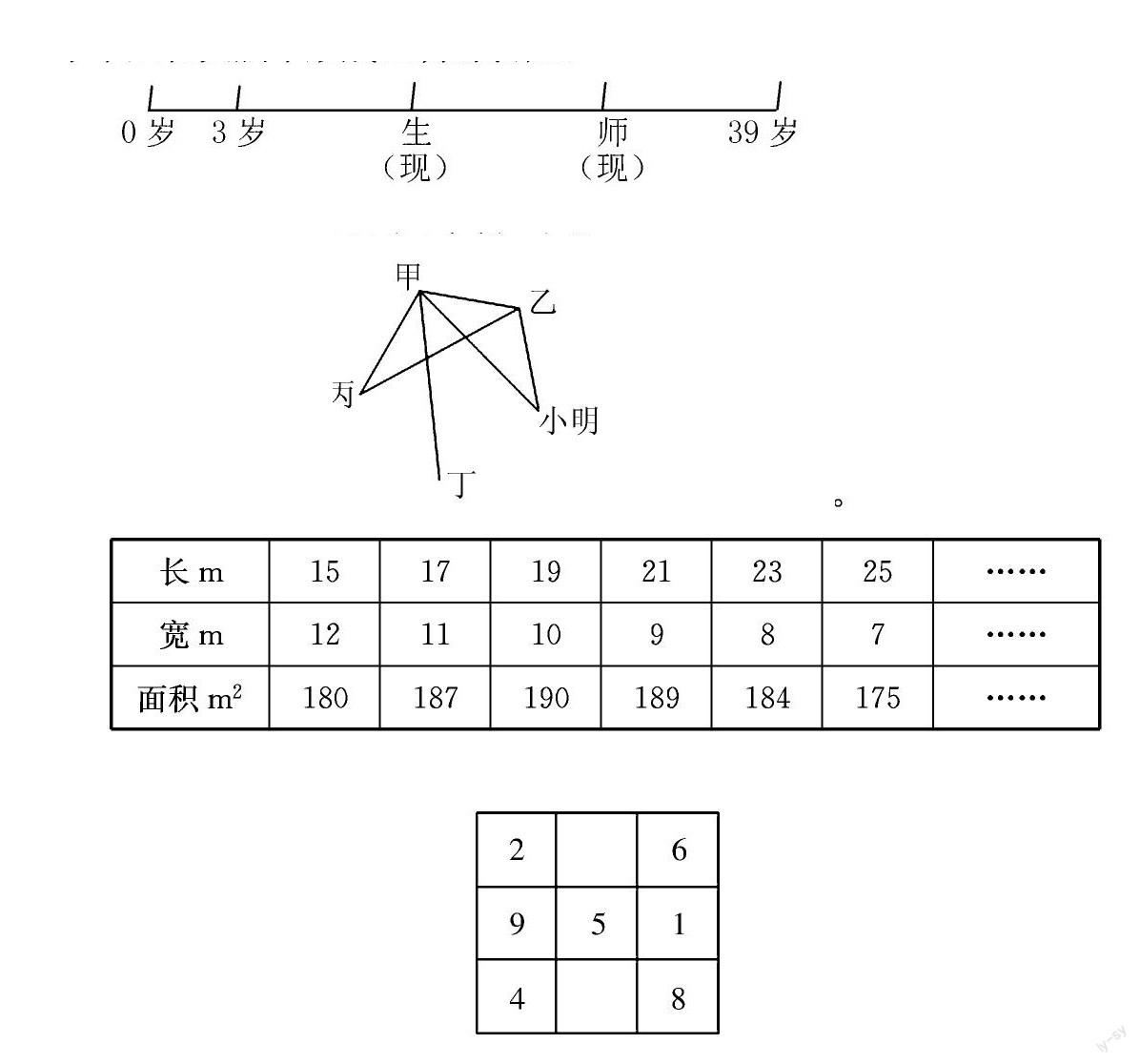
从0岁开始画起，学生3岁，老师是学生现在的年龄。中间存在着一个年龄差。而今年老师与学生的年龄也同样存在着相同的年龄差。当学生长到老师的年龄时，老师已39岁了。又相隔一段年龄差。也就是说，39-3=36岁实际上就是师生之间年龄差的3倍，所以年龄差应该是（39-3）÷3=12岁。这样可以推理出老师今年的年龄就是39-12=27岁。

又如：“甲、乙、丙、丁和小明一共五人进行羽毛球比赛，每两人比赛一场，比赛中途做了一次统计：甲比了4场，乙比了3场，丙比了2场，丁比了1场。这时小明比赛了几场？”这道题如果老师不借助描点画图连线，学生在理解上就会无从下手，丈二和尚摸不着头脑。根据题意可以用点来代替甲、乙、丙、丁、小明5人，用连线法画图如下：

甲比了4场，说明甲与其他4人分别比赛了1场。根据丁比了1场，说明丁只能跟甲比一场，其余都没有比。根据乙比了3场，可知乙与甲、丙、小明各比了1场。丙比了2场，很明显从图中可以看出丙与甲、乙各比赛了1场。由图可以推理出，此时小明只与甲、乙各比了1场，即小明在中途统计时只比赛了2场。

三、通过枚举，合情推理

小学数学教学中，一一枚举，可以清楚地看出一些数量前后变化规律，有助于问题的解决。如“张大伯用一根39米长的草绳靠一面墙围成了一个长方形篱笆，长与宽都取整米数，当长=（ ）米，宽=（ ）米时，围成的长方形篱笆面积最大？

教师可启发学生通过列表枚举去自主探究。

长m151719212325……

宽m121110987……

面积m2180187190189184175……

通过列表，可以看出，当长等于15米，宽等于12米时，长方形面积是180平方米。当长等于19米，宽等于10米时，长方形篱笆的面积最大是190平方米。当长分别为21米、23米、25米，长方形面积由189平方米逐步减少到175平方米。

有些题目，在枚举时，要适时地进行调控、矫正、推理要合乎情理。

如：“将“1～9”九个数分别填入下面的九宫格中，使九宫格中横排、竖排、对角线上的三个数之和分别都相等。”

要把“1～9”九个数填入右图中，使横、竖、对角线上的三个数之和都相等。可以先求出1+2+3+……+9的和是45，每一排之和是45÷3=15。我们可以来枚举一下，1～9九个数哪三个数相加的和等于15呢？

①枚举如下：1+9+5=15 2+8+5=15 3+7+5=15 4+6+5=15，与5相加的另外两个数只有这四组。由此可以推理出九宫格中中间一个数是5。也只有5在中间才能保证四种情况即横、竖排及两条对角线上三个数之和都等于15。

②枚举：9+2+4=15 8+1+6=15 8+3+4=15 7+6+2=15；

通过观察思考：可以知道以上8组数中，与5相加的数有4组，与8相的数有3组，与6相加的数也有3组；分别是A组2+8+5=15，8+1+6=15，8+3+4=15；B组4+6+5=15，7+6+2=15，8+1+6=15。这样我们可以大胆推断8与6都在九宫格的四角上。只有在角上，才能保证横排、竖排及一条对角成上的三个数之和都等于15。但是8与6又不能在一条对角线的两个角上，因为这样6+8+5=17，和就不等于15了，不符合要求。为此，8与6在一排上的两个角上，中间只能是1。这样一推理，就很快推理出8、5、2一组，6、5、4一组，1、5、9一组。填起来就很容易了。显然，列举时教师要引导学生不重复，不遗漏，重视培养学生有序列举的习惯。

四、建立模型，猜测推理

数学习题中，有些题要思考路径，让学生在头脑中先建立模型，再顺藤摸瓜，猜测推理。

如：在等号左边填上合适的运算符号和括号，使计算结果等于右边的数。

（一）3 3 3 3=1， （二）3 3 3 3=2。

我们在解这类题目时，可以从结果入手，通过建立模型来解决问题。

先看“3 3 3 3=1”，要使4个3的运算结果等于1，可以这样想，3与1之间有什么关系？很显然：3-2=1，这就是模型。我们只需要将最前面的3留下，剩下的3个3凑成2就行了。即：3-（3+3）÷3=1。当然也可以建立模型“0+1=1”，即3-3+3÷3=1。也可以建立模型“1×1=1”，即（3÷3）×（3÷3）=1。再来看“3 3 3 3=2”，可以建立模型1+1=2，即3÷3+3÷3=2；也可以建立模型5-3=2，但是前三个3凑不成5，这样的模型在实践探究中需要调整。

五、演示归纳，类比推理

杜威说：“经验就是教育的创造或改组。”数学教学中对学生的思维训练有时可以先借助实物演示，然后根据学生已有的认知水平与生活经验归纳、类比，让学生合情推理。

如教学：“有一个大正方体，在它的表面涂上颜色，然后将大正方体切割成棱长是1厘米的小正方体，已知两面都涂色的小正方体共有60个，求原大正方体的体积是多少立方厘米？”

教者可先让学生观察实物图，然后操作演示。启发学生思考这样一个数学问题，看“两面涂色的小正方体在大正方体的什么位置上？”学生观察得出：两面涂色的小正方体都在大正方体的12条棱上。但每条棱的两端两个小正方体都是三面涂色，不符合要求。通过观察，可以得出大正方体每条棱上有5个两面涂色的小正方体。那么可以推理大正方体12条棱上共有两面涂色的小正方体个数是5×12=60个。这与题目中所给的已知条件完全相同。通过归纳、类比，我们不难得出：大正方体12条棱的长度都相等，每条棱上两面涂色的小正方体个数是相同的，就是60÷12=5（个）。由于大正方体每一条棱的两端都有一个三面涂色的小正方体，由此可以推理出大正方体的一条棱上就由5+2=7个小正方体组成，即大正方体的棱长就是7×1=1（厘米）。这样大正方体的体积就是73=343立方厘米。

当然，合情推理在数学教学中它不是孤立存在的，有时与演绎推理、逻辑推理综合应用。合情推理只有植根于学生基本活动经验这块沃土，才能开出更加艳丽的花朵，结出丰硕的果实。