几类微分算子的一般表示
武 进,李云霞,张二喜
(成都理工大学管理科学学院,四川成都 610059)
几类微分算子的一般表示
武 进,李云霞,张二喜
(成都理工大学管理科学学院,四川成都 610059)
梯度,散度,旋度这三个概念不仅在物理学中有着重要的地位,同时在微分学中也地位突出。首先介绍了弧长微元,面积微元,体积微元在不同的坐标系下的表示。其次从物理学的角度阐明了梯度,散度,旋度的物理意义让我们对梯度,散度,旋度有一个新的认识,最后将梯度,散度,旋度在不同坐标系下表示,从不同的角度去研究,从而有一个更加通俗易懂的认识。
弧长微元;面积微元;体积微元;梯度;散度;旋度;一般表示
1 弧长微元,面积微元,体积微元
1.1 直角坐标系下的弧长微元,面积微元,体积微元[1-4]

进而可得

如图1所示建立直角坐标系并作图:

图1 直角坐标系
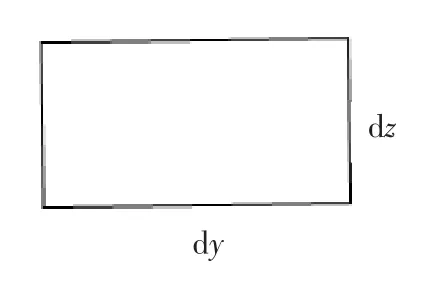
图2 平行六面体的主视图
1.2 一般坐标系下的弧长微元,面积微元,体积微元

要使变换有意义则其雅克比行列式:

其中

于是可得弧长微元:
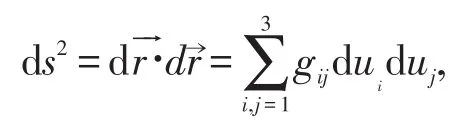
且gij=0(i≠j)即有

图3 直角坐标系
则有弧长微元

图4 平行六面体的主视图
于是可以得到前后面面积微元:

同样左右面面积微元:

上下面面积微元:

例1求圆柱坐标下的弧长微元,体积微元。
解设给出的向量

选取向量组


图5 圆柱坐标系中的一角
例2求球坐标下的弧长微元,体积微元。
解设给出的向量

我们选取向量组

2 几类微分算子的一般表示
2.1 梯度的一般表示[5-8]
2.1.1 梯度的物理意义
由Diragance定理:
2.1.2 梯度在一般坐标系下的表示
考虑函数f从点A(u1,u2,u3)变化到点由泰勒展式可知两点间的差分:

A,B两点之间的距离用向量表示为:

用差分表示为:

因而

这便是梯度在一般坐标系下的表示。
2.1.3 梯度在圆柱坐标,球坐标系下的表示
(1)梯度在圆柱坐标系下的表示。
由于在圆柱坐标下拐点

故梯度:

(2)梯度在球坐标系下的表示。
由于在球坐标下拐点

故梯度:

2.2 散度的一般表示
由Gamssdiragdnce定理:
2.2.1 垂直坐标系下散度的一般表示:
2.2.2 散度在一般坐标系下的表示
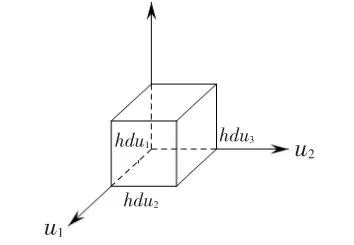
图6 直角坐标系
2.2.3 仿照垂直坐标系下散度一般表示的方法,则

证明不妨固定的方向由Gamssdiragdnce定理可知沿着方向的通量为,当Δh1→0时;同理当时
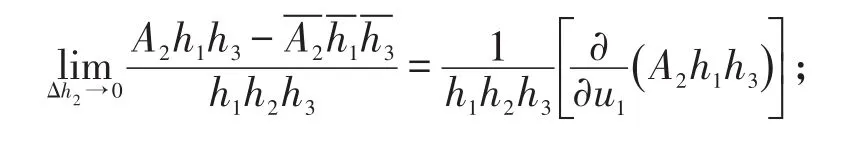

故

2.2.4 散度在圆柱坐标,球坐标系下的表示
(1)散度在圆柱坐标系下的表示:
圆柱坐标系下记向量

(2)散度在球坐标系下的表示:
球坐标系下记向量

则

2.3 旋度的一般表示
2.3.1 旋度的物理意义
由stoke定理:,即c是s

通过上式我们可知旋度的物理意义为单位面积之环流。的边界,两边积分可知:
2.3.2 一般坐标系下旋度的表示


上式为旋度的一般表示。
[1]葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007.
[2]仇庆文,陈恕行.傅里叶积分算子理论及其应用[M].北京:科学出版社,1985.
[3]P V VINOGRADOVA,A G ZARUBIN.Asymptotic estimates of a projection-difference method for an operator-differential equation[J].Journal of numerical mathematics,2013,21(3):181-200.
[4]杨秋霞.关于几类常微分算子特征值的研究[D].呼和浩特:内蒙古师范大学,2007.
[5]许美珍.常微分算子理论的发展[D].呼和浩特:内蒙古师范大学,2011.
[6]Xu X.Differential-operator representations of S_n and singular vectors in Vermamodules[J].Algebras and representation theory,2012,15(2):211-231.
[7]Kalantarov V K,Yilmaz Y.Decay and growth estimates for solutions of second-order and third-order differential-operator equations[J].Nonlinear Analysis:An International Multidisciplinary Journal,2013,89:1-7.
[8]马天.偏微分方程理论与方法[M].北京:科学出版社,2011.
〔责任编辑 高海〕
General Representation of Several Types of Differential Operators
WU Jin,LI Yun-xia,ZHANG Er-xi
(College of Managemen Science,Chengdu University of Technology,Chengdu Sichuan,610059)
These three concepts of gradient,divergence,curl play an important role not only in physics,but also prominent in the differential calculus.This article first introduced,arc length element,with an area of infinitesimal element of volume expressed in dif⁃ferent coordinate systems,for later in the gradient,divergence,curl in different coordinate systems is generally fully prepared.Second,from the point of view of physics we clarify the gradient,divergence,curl the physical meaning,we have a new understanding of the gra⁃dient,divergence,curl.Gradient,divergence,curl are shown different coordinate systems and studied from different angles,making it a more user-friendly understanding.
arc length element,area element,the element of volume,gradient,divergence,curl,generally express
O175.8
A
1674-0874(2015)03-0020-04
2015-02-24
武进(1985-),男,四川泸县人,硕士,研究方向:基础数学。

