收益曲线变动的宏观经济效应研究

周生宝，刘书舟

（1.山西大同大学数学与计算机科学学院，山西大同037009；2.西北政法大学经济学院，陕西西安 710122）

收益曲线变动的宏观经济效应研究

周生宝1，刘书舟2

（1.山西大同大学数学与计算机科学学院，山西大同037009；2.西北政法大学经济学院，陕西西安 710122）

通过研究我国收益曲线与宏观变量的关系，发现宏观变量与潜在因子高度相关，宏观变量是利率期限结构变动的主要驱动因素。政策利率的增加导致收益曲线向上转变，央行能影响所有收益曲线。斜率含有收益曲线短期的大量信息，汇率变化对收益曲线有显著解释能力，通胀和产出缺口的增加和减小会使利率升高和降低。

期限结构；收益曲线；宏观变量

宏观经济与金融市场密切相关，正确认识宏观经济变量和微观金融变量的关联关系对宏观经济、金融市场研究者以及货币政策制定者是具有挑战性的课题。短期利率是金融市场和宏观经济联系的桥梁，考察其期限结构的特征、宏观变量在其变动中的作用是恰当的切入点。

微观视角中，利率期限结构常用潜在因子的函数来刻画，目的在于预测未来利率与资产定价，但该理论认为期限结构的变化主要由风险溢价驱动，宏观变量的作用完全被忽略，潜在因子与宏观变量间的联系没有被考虑。宏观视角下则认为短期利率由通胀和产出缺口决定，而长期利率由短期利率的未来预期决定，但这种研究忽略了金融风险、信用风险的溢价变化对收益的影响。所以使宏观变量和期限结构结合起来是可行和有益的尝试。

Ang和Piazzesi[1]借助含宏观变量的仿射因子模型研究表明，在短期和中期收益曲线的变化中宏观变量起着重要作用。Hordchl[2]以只含宏观因子的期限结构模型分析了德国利率数据，发现宏观因子对期限结构的影响机制各不相同，通胀和产出冲击影响收益曲线的斜率，货币政策冲击影响曲线的曲率。Rudebusch和Wu[3]用结合新凯恩斯预期理论的仿射无套利模型进行研究，认为利率期限结构和宏观变量有密切联系，都受宏观变量影响，同时收益曲线的上升伴随着通胀和产出缺口的增加。这些表明宏观变量影响着利率期限结构，而利率变化反映出市场参与者对货币政策看法。不过这种研究主要集中于欧美国家。

我国利率市场化正不断深入，利率的确定与其特征越来越被各方所关注。如吴吉林[4]等、袁靖和薛伟[5]、周生宝[6]等从不同角度考察了宏观变量对收益曲线的解释能力及我国收益曲线的分解问题。随着市场经济改革的深入，利率的资源配置功能凸显，宏观经济与利率期限结构的关系研究更显重要。而且就开放的经济环境来说，汇率对宏观经济与金融市场有不容忽视的影响，然而汇率与收益曲线的关系研究并不多见。

基于此，本文考察2003年初到2014年底利率期限结构和宏观变量的关系，这期间包含了一次较大的经济危机，也包含了我国货币政策从从紧到稳健不断调整变化的过程。

1 数据与DNS模型

国债收益用连续复合月度数据从2003年初到2014底，期限为1,3,6,12,24,36个月，用yt(n)表示。

宏观变量为通胀率、经济增长率、产出缺口、汇率及政策利率。通胀率为πt=logCPIt-logCPIt-12，CPI经季节调整。经济增长率为GDP对数增长率grtGDP=logGDPt-logGDPt-12，月度GDP由三次样条插值计算。产出缺口用gapGDPt表示，用HP滤波法除去logGDP趋势，时期t的缺口只用HP滤波拟合到时期t，这能确保产出缺口数据不依赖于未来数据信息。汇率为直接标价法，et表示名义汇率，rert表示真实汇率。政策利率取央行发布的同业拆借隔夜利率，用rt表示。

三因子NS模型受到国内外金融机构的广泛关注，可表示为：

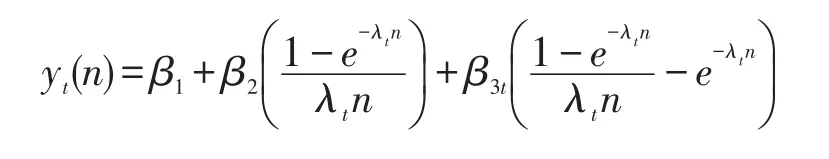
βi,i=1,2,3，λt为参数。如果βi时变则NS模型变为动态NS即为DNS模型：

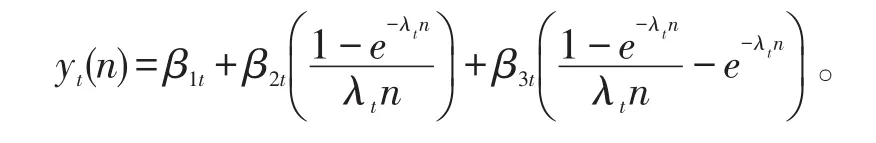
这种改进能使模型更好的刻画整条收益曲线的动态性。其中，λt较小则曲线有较小的指数衰减性，反之亦然，且较小和较大的λt分别能较好的拟合收益曲线的短期和长期。潜在因子β1t,β2t,β3t，可分别称为水平、斜率、曲率因子。β1t的增加会使所有收益曲线相等增加，它会改变收益曲线的水平，且其系数为1永不会衰减，可被看作长期因子。β2t被看为长期减去短期，而短期利率相对于长期利率会使β2t的负载增加更多，所以β2t的变化改变曲线的斜率，且β2t的系数从1开始但会很快单调减小为零，被看作短期因子。β3t的增加会使中期收益增加的比短期和长期增加要多，因此它与曲率密切相关，且β3t的最大值点由λt决定，其系数从零开始逐渐增加再减小为零，可被看作中期因子。

最优的λt会使β3t达到最大，所以估计参数θ={λt,β1t,β2t,β3t}可先固定λt，因为数据最大36个月，最小为1个月，6和12个月是合适的，所以取n=8，计算得λt=0.4583，其余参数θ={β1t,β2t,β3t}采用最小二乘估计。

实证角度看，最长期利率可看作水平因子的经验值，文中为yt(36)；最长和最短期限收益的差可为短期因子斜率的经验值，这里为yt(1)-yt(36)，而yt(6)+yt(12)-yt(1)-yt(36)可作为中期因子的经验值。文中估计的β̑1t,β̑2t,β̑3t与其经验值的相关性为0.98、0.98、0.96，两者高度相关。图1至3分别为因子估计值与经验值，表明模型对利率数据刻画较好。对潜在因子做单位根检验，ADF检验结果表明各因子估计值平稳。

2 收益曲线与宏观变量的关系

分析宏观变量和分解出的潜在因子的相关性可以理解宏观变量在收益曲线结构变化中的作用。

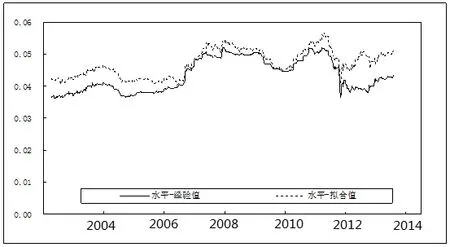
图1 估计的水平因子与其经验值

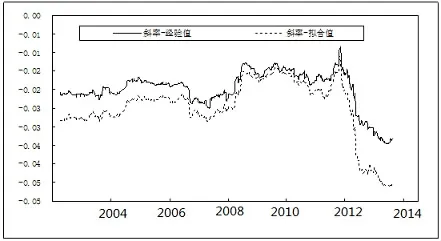
图2 估计的斜率因子与其经验值

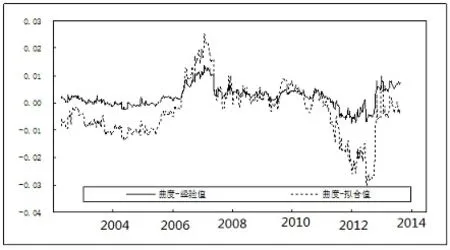
图3 估计的曲率因子与其经验值

由表1来看，首先β1t和β2t有较高相关性，表明它们可能被共同的因子影响。通胀与水平因子的相关性为0.87，说明全部收益曲线对通胀的变化都较敏感。另一方面，Diebold et al[7]（2006）认为水平因子可作为债券市场参与者对通胀的看法，这样水平因子的增加意味着会伴随近期经济的增长。然而如果中央银行对通胀预期上升做出反应而提高政策利率，就会限制通胀和产出缺口的增加。Rudebusch和Wu[3]（2008）认为央行可以把水平因子当作能被市场参与者觉察到的通胀目标，相应的文中发现通胀与水平因子的相关性为0.87，这较为合理。产出缺口和水平因子的相关性为0.50，这与泰勒规则一致。政策利率与水平因子的相关系数为0.95，说明政策利率的增加导致收益曲线向上转变。通胀和产出缺口的增加必伴随政策利率的增加，这会使利率升高。

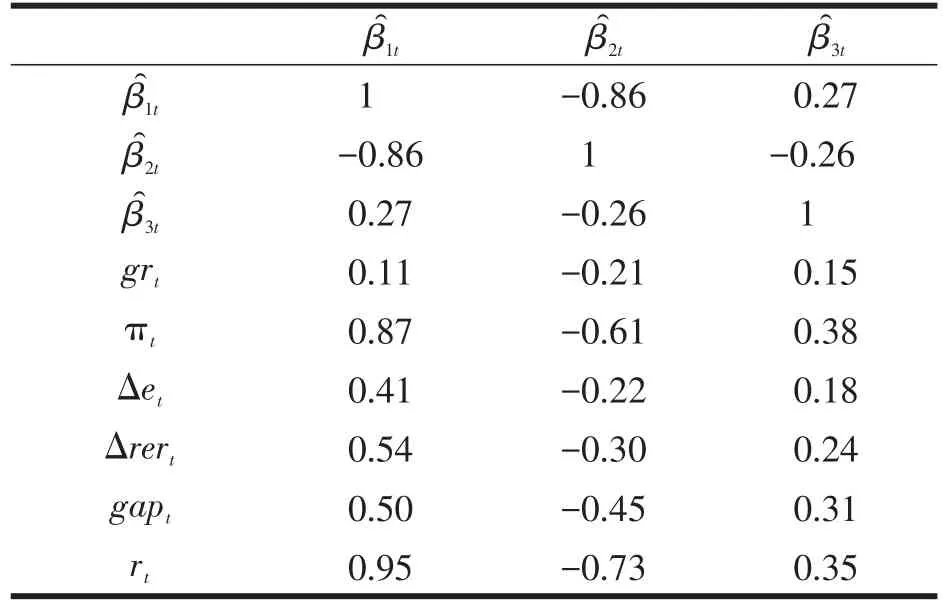
表1 相关系数值表

通胀与斜率因子的相关性显著为-0.61，可见斜率因子对未来通胀有显著预测能力，与此相应产出缺口和斜率因子的相关性为-0.45。政策利率和斜率因子的相关性为-0.73，表明政策利率对长期利率的影响高于对短期利率的影响。Rudebusch和Wu[3]（2008）认为，美国货币政策对斜率因子有较强但较短的影响，但对水平因子的影响不显著，这样美联储主要是通过改变斜率来影响收益曲线的。本文发现我国央行能影响短期亦能影响长期收益曲线。

汇率通过影响进出口商品和总需求成为影响通胀的另一途径，从而导致名义汇率变动对经济参与者预期有较大影响。本文发现汇率变化与收益曲线水平有正相关性，真实和名义汇率与水平因子的相关性为0.54和0.41，所以汇率水平的升高导致收益曲线上升。

宏观变量与曲率因子的相关性通常较小，而且现阶段对两者的关系没有统一看法。本文曲率因子与通胀、产出缺口、政策利率的相关性分别为0.38、0.31、0.35。Kaya(2013)[8]认为曲率因子可以代表一个独立的货币政策因子，研究显示曲率因子的增加与稳健货币政策正相关。本文的正相关与此一致。Moench(2012)[9]认为曲率因子反应了经济的周期波动，对曲率因子的负冲击将伴随经济增长的放慢。本文曲率因子与产出缺口正相关与此也一致。

如果宏观变量是真正的因子，做收益对宏观变量的回归将有较好的拟合效果，做回归：

n=1,3,6,12,24,36，εt为独立正交因子，xt为宏观变量向量。先用通胀和产出缺口做宏观变量，结果如表2所示。

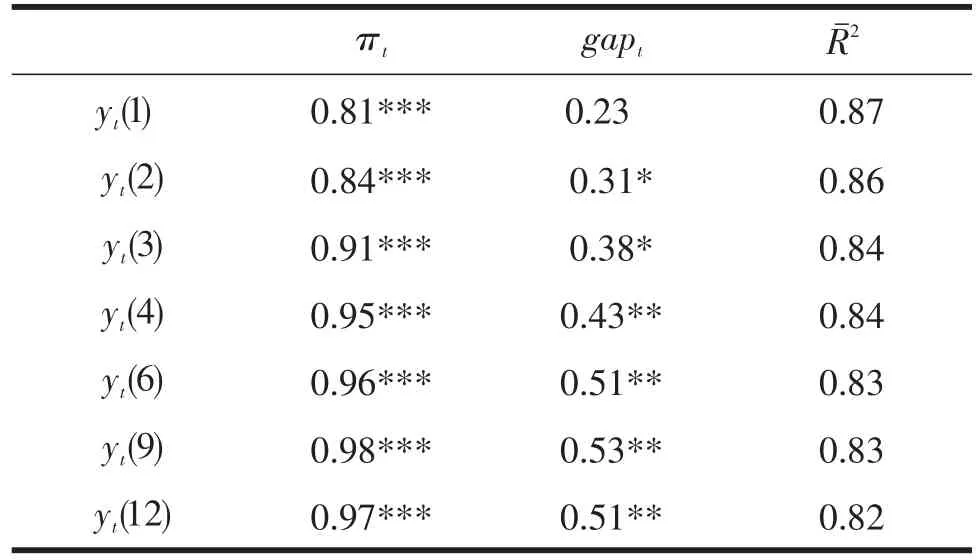
表2 不含汇率变动的回归结果

通胀因子的系数都是显著的，但产出缺口除最短期外都是显著，修正的R2较高且随期限增加逐渐从0.87降到0.82。系数符号与水平因子和宏观变量的相关性分析一致，通胀和产出缺口的变动使全部收益上升或下降。通胀系数的大小随期限的增加而变大，这与通胀与斜率因子具有负相关性一致。

以汇率作为第三个因子，可分析汇率在收益曲线变动中的作用。式1中加入Δet，结果如表3。加入Δet增加了模型对收益的解释能力，特别是对短期和中期。Δet系数显著为正，回归系数将随期限增加而减小，与汇率变化和斜率因子正相关一致，建议汇率也是影响收益曲线变动的重要变量。

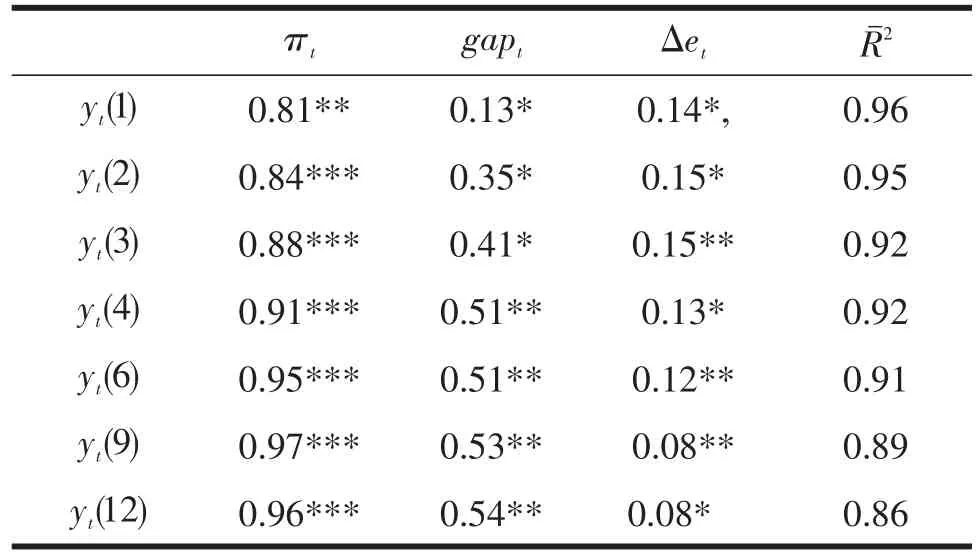
表3 含汇率变动的回归结果

考察残差与各因子的关系，发现短期中未被解释的部分主要与斜率相关，而收益曲线长期未被解释的部分与水平因子高度相关，表明曲线斜率含有短期的丰富信息，也说明增加汇率能显著增加对短期曲线的拟合优度。

3 结论

文章应用DNS模型从收益曲线分解出了水平、斜率、曲率因子。研究发现宏观变量与潜在因子有较高相关性，宏观变量是收益曲线期限结构变化的主要驱动因素。水平因子反应收益曲线的长期，央行可以把它当作能被市场觉察到的通胀目标。政策利率的增加导致收益曲线向上转变，央行有影响所有收益曲线的能力。斜率含有收益曲线短期的大量信息，汇率对收益曲线具有显著解释能力，所以可以通过影响斜率或进行汇率干预来影响收益曲线。通胀和产出缺口的增加和减小会使利率升高和降低，通过限制缺口的增加能抑制经济过快增长或通胀预期的上升。

[1]Ang A,Piazzesi M.A No-arbitrage Vector Autoregression of Term Structure Dynamics with Macroeconomic and Latent Variables[J].Journal of Monetary economics,2003,50:745-787.

[2]Hordahl P O T,David V.A Joint Econometric Model of Macroeconomic and Term Structure Dynamics[J].Journal of Econometrics,2006,131:405-444.

[3]Rudebusch G D,Wu T.A Macro-Finance Model of the Term Structure[J].Monetary Policy and the Economy,2008,118:906-926.

[4]吴吉林，金一清，张二华．潜在变量、宏观变量与动态利率期限结构-基于DRA模型的实证分析[J]．经济评论，2010(1)：80-88．

[5]袁靖，薛伟.中国利率期限结构域货币政策联合建模的实证研究[J].统计研究，2012(2)：42-47．

[6]周生宝，王雪标，郭俊芳．我国通胀预期与通胀的动态关联性-基于宏观金融模型的研究[J].中国管理科学，2014(22)：27-35．

[7]Diebold F X,Rudebusch G D,Aruoba S B.The Macroeconomic and the Yield Curve:a Dynamic Latent Factor Approach[J].Journal of Econometrics,2006,131:309-338.

[8]Huseyin Kaya.Forecasting the Yield Curve and the Role of Macroeconomic Information in Turkey[J].Economic Modeling,2013(33):1-7.

[9]Moench E.Term Structure Surprises:the Predictive Content of Curvature Level and Slope[J].Journal of Applied Econometrics,2012,27:574-602.

〔责任编辑 高海〕

Study on the Macroeconomic Effects in the Changes of Yield Curve

ZHOU Sheng-bao1,LIU Shu-zhou2
（1.School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009;2.School of Economics,Northwest University of Politics and Law,Xi′an Shaanxi,710122）

This paper investigates the relationship between China's yield curve and macro variables.We find that the macro vari⁃ables exhibit highly correlation with the latent factors and are the main driving force for the changes of the term structure.The increas⁃ing changes in the policy rate will lead to the increase of the yield curve,and the central bank has ability to affect the entire yield curve.The slope factor contains plenteous information on the short end of the yield,and the changes in exchange rate have significant explanatory power in model,and the changes in Inflation and the output gap will lead a corresponding change in rate.

term structure;yield curve;macro variable

F810

A

1674-0874(2015)03-0005-04

2015-03-09

国家自然科学基金项目[71273044];山西大同大学博士科研启动基金项目[2013-B-03]

周生宝（1979-），男，山西闻喜人，博士，讲师，研究方向:金融风险与管理。