关于环的两个元素和的性质的进一步讨论

林大华,戴立辉

（闽江学院数学系，福建福州350108）

关于环的两个元素和的性质的进一步讨论

林大华,戴立辉

（闽江学院数学系，福建福州350108）

结合环元素的乘法运算，对环中两个元素和的性质作进一步的讨论，得到了若干结果。

环；元素之和；性质

环是具有加法和乘法两个代数运算的代数结构，加法在环理论中占有极其重要的地位。由于环关于加法构成的代数结构是加群，因此，环R中的两个元素a,b的和a+b具有加群元素和的所有性质，所以单纯讨论环中两个元素和的性质意义不大。本文试图通过结合环元素的乘法运算来讨论环中两个元素的和，从而进一步得到环的两个元素和的若干性质。

1 预备知识

用R表示环；当R有单位元时，用1表示R的单位元；用N表示自然数集合。

定义1[1]设R是环，a∈R。

（1）若存在正整数k，使得ak=0，则称a是幂零元。

（2）若a2=a，则称a是幂等元。

（3）若R有单位元，且存在a-1∈R，使得aa-1=a-1a=1，则称a是可逆元，称a-1是a的逆元。

（4）若a≠0，且存在 0≠b∈R（0≠c∈R），使得ab=0(ca=0)，则称a是左（右）零因子。

定理1[2]设R是有单位元的环，a,b∈R，则

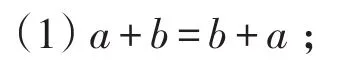
（2）当ab=ba时，

（3）当ab=ba时，，其中k≥2,k∈N；

（4）当ab=ba时，

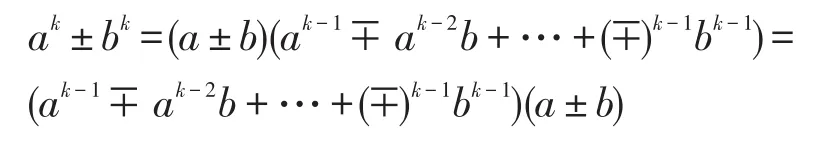
其中k≥2,k∈N。

推论1设R是有单位元的环，a∈R，则

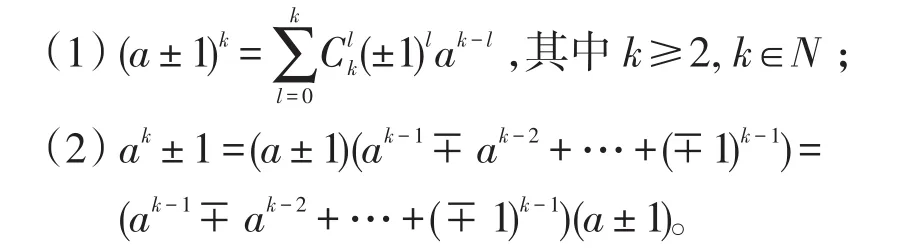
定理2[3]设R是有单位元的有限环，a,b∈R，若ab=1，则ba=1。

2 主要结论

定理3设R是环，a,b∈R，则

（1）当a,b是中心元时，a±b也是中心元。

（2）当a,b是幂零元，且ab=ba时，a±b也是幂零元。

（3）当a,b是幂等元，且ab=ba时，a+b也是幂等元⇔ab=0。

证明（1）因为∀r∈R，有ar=ra，br=rb，所以有

(a±b)r=ar±br=ra±rb=r(a±b)，故a±b也是中心元。

（2）由a,b是幂零元知，存在正整数m,n，使得am=0,bn=0。又(a±b)m+n=0，故a±b是幂零元。

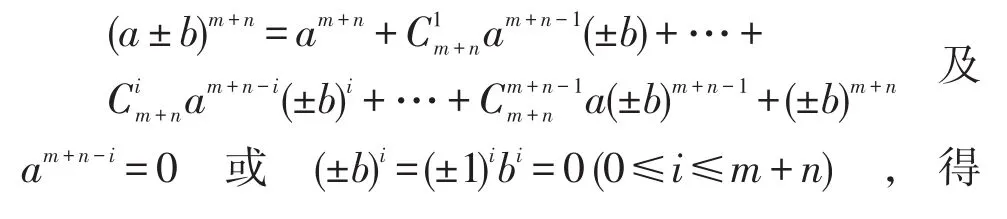
（3）由a,b是幂等元，得，所以a+b是幂等元

定理4设R是有单位元的环，且ab=ba，则

（1）当a是幂零元，b是可逆元时，a±b是可逆元。

（2）当a(≠0,1)是幂等元时，a-1既是左零因子，又是右零因子。

证明（1）因为a是幂零元，所以存在正整数k，使得ak=0，于是

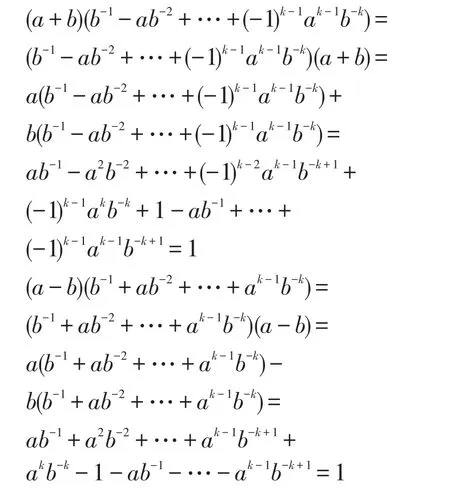
故a±b是可逆元，且

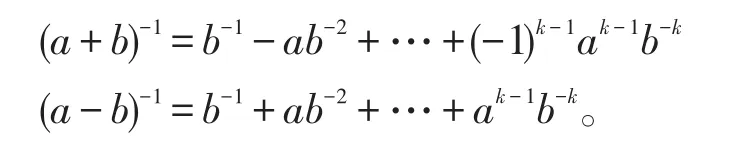
（2）因为a是幂等元，所以a2=a，于是，从而由可知，a-1既是左零因子，又是右零因子。

推论2设R是有单位元的环，如果是幂零元，则a±1是可逆元，且当ak=0时，有

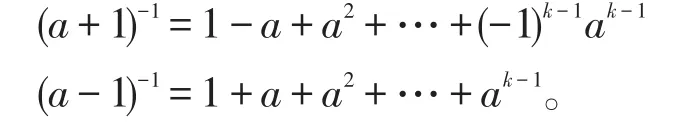
定理5设R是有单位元的环，a,b,a+b是R的可逆元，则也是R的可逆元，且

证明由，得，所以由a是可逆元知，是a的逆元，于是有，再由条件可知可逆，由此可知是的逆元，从而有

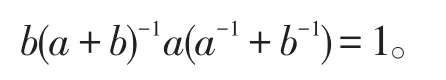
定理6设R是有单位元的环，，则

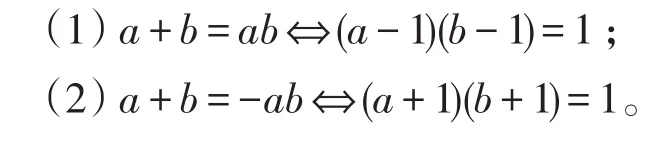
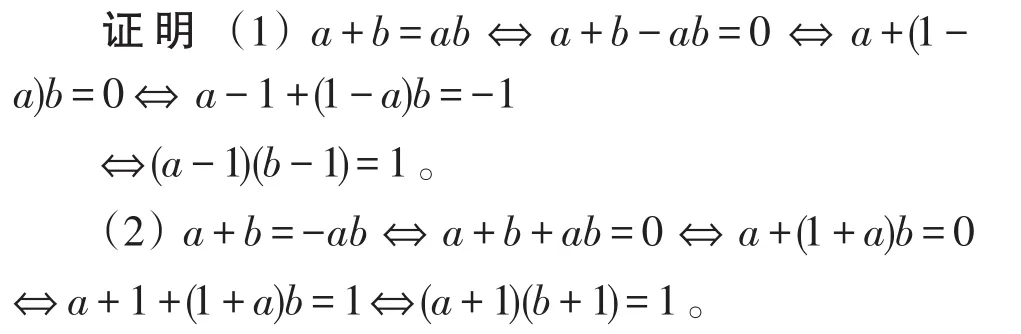
推论3设R是有单位元的有限环，a,b∈R，则

证明由定理6及定理2可得：

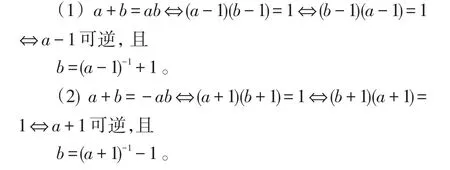
推论4设R是有单位元的环，a,b∈R，则

（1）当R是有限环时，若a+b=ab（或-ab），则ab=ba。

（2）当a-1（或a+1）是可逆元时，若a+b=ab（或-ab），则ab=ba。

证明（1）因为a+b=ab，所以由推论3，有b-1=(a-1)-1，于是

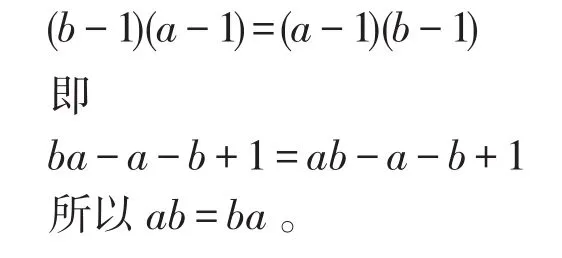
定理7设R是有单位元的有限环，则

证明（1）由推论4，有，所以当a是可逆元时，有，于是有，因此b是可逆元，且，即。

反之，当b是可逆元时，有，于是有，因此a是可逆元，且，即。

反之，当b是可逆元时，有，于是有，因此a是可逆元，且，即。

[1]熊全淹.近世代数[M].上海：上海科学技术出版社，1978.

[2]韩士安,林磊.近世代数[M].北京：科学出版社，2004.

[3]杨子胥，宋宝和.近世代数习题解[M].济南，山东科学技术出版社，2003.

Ker words:ring;sum of two elements;property

〔责任编辑 高海〕

Further Discussion on Property of the Sum of Two Elements in Ring

LIN Da-hua,DAI Li-hui
(Department of Mathematics,Minjiang University,Fuzhou Fujian,350108)

In this paper,we deeply discuss property of the sum of two elements by multiplication in ring.

O153.3

A

1674-0874(2015)03-0018-02

2015-02-27

福建省中青年教师教育科研项目[JB13164];闽江学院2013年度教育教学改革研究项目[MJUB2013033]

林大华（1959-），男，福建福州人，副教授，研究方向:代数学。