MQ径向基函数的理论、方法及应用∗

乔远阳，吴技莲，冯新龙

(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)

0 引言

径向基函数(Radial Basis Function,简称RBF)是一个取值仅依赖于离原点距离(本文使用欧氏距离)的实值函数,即或者还可以是到任意点的距离,其中称为中心点,即其研究的主要工作就是研究该函数张成的空间及其性质,并如何利用这个空间来解决一般对象的描述问题.径向基函数是处理多元函数逼近问题的一种有效方法.事实上,它是通过定义在[0,∞)上的一元函数φ与Rd上的欧几里德范数来表示元函数其中向量因此,用径向基函数处理多元函数逼近问题具有效率高,运算简单,易于编程,在计算机中储存方便以及各向同性,不依赖于网格,求解精度高等优点,其在函数逼近、偏微分方程数值解、神经网络、小波、多尺度分析以及地球物理学、测绘学、遥感与信号处理、图像处理、机器学习、天文学与采矿等领域得到了广泛的研究和应用.

目前在解决实际问题中常用到的数值方法有:有限差分法、有限元法、有限体积法、边界元法、无网格法等.虽然前四种方法解决了众多的科学和工程计算问题,但它们存在一个共同的缺点:求解过程中每次都需要剖分网格,计算工作量大,尤其是三维问题.所以要想彻底解决这些方法面临的网格重构问题,就应该避免使用网格.于是,无网格思想就被提出来了,并在近年来得到了迅速发展.目前,具有代表性的无网格方法主要有光滑粒子动力学法、无单元Galerkin法、重构粒子法、单位分解法、RBF法等十余种,其中无单元Galerkin法、RBF法和重构粒子法是无网格法研究的主流方向.RBF方法是以径向函数为插值基函数,在求解中采用配点形式,无需背景网格支持的方法.此方法的优点是不受单元形状的限制,在场量变化剧烈的地方,可以很容易地增加中心点的密度,因此避免了网格剖分在求解过程中的困难.

基于RBF的诸多优点,国内外研究人员进行了大量的科学研究并取得了丰硕成果,在此主要介绍RBF在计算数学上的应用.径向基函数的研究是从径向基函数插值开始的,以下章节中会给出径向基函数插值的基本理论结果.20世纪60年代,由Hardy[1]提出的MQ方法是一种无网格配置方法,目前它是径向基函数无网格法的主流.Hardy最早将其用于散点曲面插值拟合.20世纪80年代初,Franke[2]对数十种散点插值法综合比较,得出MQ方法是具有最好效果的方法.在之后的研究结果中,Micchelli[3]给出了RBF插值的可解性证明;Schaback[4]进一步研究了插值的存在性、唯一性和收敛性问题,使得RBF插值理论日趋成熟;此外,吴瑞丰[5]等人研究并构造了高精度RBF拟插值算子;Kansa[6]把径向基函数引入配点法中,首次成功地用以求解双曲、椭圆和抛物型问题;此后,RBF方法在偏微分方程求解方面引起了广泛关注,Franke[7]和Schaback首先建立了RBF方法在求解偏微分方程上的理论基础;Wu[8,9]主要从理论上研究了该方法的可解性和误差限.但是,Dubal[10]和Fornberg[11]进一步研究了这类基于RBF的方法,发现随着秩的增加,系数矩阵会变得病态,为了解决这个问题,Kansa[12]提出用块分解和LU分解格式取代全局求解器,从而避免病态矩阵的产生.此外,在前人工作的基础上,张云新[13]和张淮清[14]分别系统地研究了RBF方法在不可压缩流体和电磁场计算中的应用.

根据定义域的不同可将径向基函数分为全域型和紧支型,全域型RBF具有连续性和无限可微等优点,在近似函数方面能获得较高的精度,相对于移动最小二乘近似,其计算量大幅减小,对散点模型适应性强,且对空间维数不敏感.这在高维空间(二维和三维)问题分析中优势更加突出.虽然RBF方法基函数中心点和配点设置灵活、程序编制简便.但由于它是一种全域型方法,离散形成的代数矩阵是满阵,故得到系数矩阵的条件数很大,不便于求解较大规模的问题.为了解决这一问题,出现了多种可行的方法,如优化调整MQ径向基函数的形状参数[12,15]、紧支径向基函数[16]以及区域分解法[17].近年来,吴宗敏[18]给出了正定紧支径向基函数的构造法则,并构造出一系列正定紧支径向基函数;Buhmann[19]给出了基于TPS函数的正定紧支径向基函数.Wendland[20]给出的正定紧支径向基函数与吴宗敏的类似,但它们具有最少的自由度.这些正定紧支RBF具有系数矩阵稀疏、带状分布的特点,有利于解决大型问题,但它们不满足完备性条件,甚至不能正确描述常应变状态.

在过去的几十年里,径向基函数方法取得了长足的发展,但在严格的数学论证、计算效率、边界条件处理等方面还不能与成熟的有限元方法相媲美.虽然径向基函数方法的理论研究还不成熟,但因它不需要背景网格支持,故在许多应用领域中具有广阔的发展前景.

在本文后面的章节中,主要讨论RBF的定义、分类、插值和应用,并着重介绍了MQ-RBF的发展历程,理论知识及迭代自适应MQ-RBF方法在间断检测上的应用.由于MQ-RBF是全域型的,离散形成的系数矩阵是满阵且条件数很大,为解决这一难题,将采用维数分裂的方法进行处理,该方法非常适合并行计算.

本文接下来的结构框架如下:第二节主要介绍RBF的基本理论知识和插值方法,第三节主要介绍MQRBF的相关知识及其在间断检测上的应用,第四节主要对RBF方法进行了总结,并探讨了其研究的发展趋势和未来可能的研究方向.

1 径向基函数

本节主要介绍RBF的一些基本概念、分类及插值方法[14,21].

1.1 基本概念

首先给出径向函数(RF)和径向基函数(RBF)如下形式的基本定义:

定义1[14]对于给定的径向函数φ满足:若则有其中φ是仅依赖于的函数,这里为Euclidean范数.

定义2[21]对于给定的和非负一元函数φ:R+→R,径向基函数是由所有形如的函数及其线性组合张成的函数空间,其中为径向函数的中心.

简单地说,RBF就是一个距离基函数,其变量为空间距离r,故具有形式简单和各向同性等优点.在特定条件下,只要选取两两不同,则就是线性无关的,故其可形成径向基函数空间中的一组基,当选取几乎充满Rd时,及其线性组合便可逼近空间内几乎所有的函数.

径向基函数按定义域的不同可将其划分为全域型和紧支型两类,其中全域型函数在插值中具有较高的精度,但不善于求解高维问题;紧支型函数则由于求解矩阵为稀疏、带状分布的，故其计算量较小,适合大型问题的求解.常见的全域型RBF如表1所示.紧支型RBF可看作是全域型函数通过一个截断多项式,在给定的连续性条件和自变量维数下截断产生的,一般要求它在给定的维数空间内正定和连续.常见的紧支型RBF如表2所示.

表1 常见全域型RBF

表2 常见紧支型RBF

其中(1−r)+定义如下:

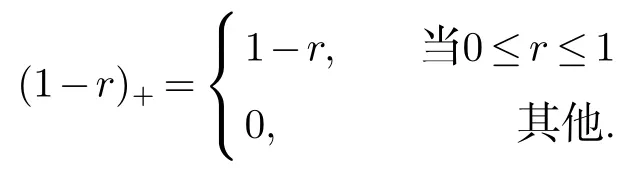
1.2 插值方法

插值法是一种非常重要且经典的函数逼近方法,RBF的研究也是从插值开始的.插值过程是通过给定的离散数据节点,寻求一个能逼近未知函数的近似函数,且要求近似函数在插值节点处的数值与原函数相等.根据给定问题条件的不同,将插值方法大体分为直接插值方法(包括拉格朗日插值和牛顿插值)和带导数条件的Hermite插值方法.对于RBF插值,与之对应的方法主要有Kansa插值、Hermite插值和拟插值等[14].RBF插值是在插值中选用径向函数作为基函数的插值方式.它最早源于1951年Kringe在矿藏领域用于沉积插值的各向同性、稳定的随机函数;随后在1971年Hardy应用多重二次插值方法,实现飞机外形曲面拟合问题并给出了MQ函数;另外,1975年Duchon从样条弯曲能最小的理论出发,提出了多元问题的薄板样条函数逼近方法.以上应用于不同领域的插值方法都为形成RBF插值奠定了基础.RBF插值的数学语言表述如下:

给定个已知节点和未知函数且其在节点上的函数值为若想对未知节点进行插值,首先需找到简单函数使得在已知节点满足插值条件:

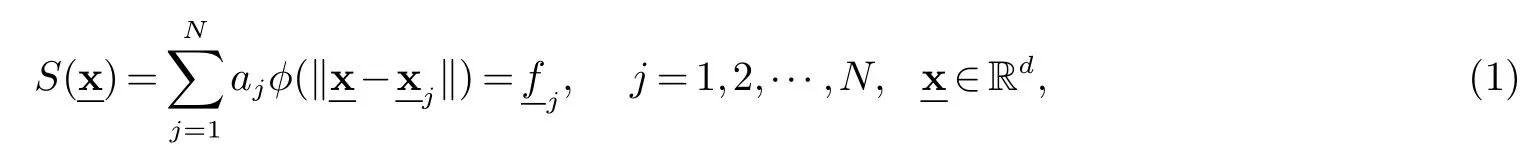
其中aj是待定系数,则方程(1)的矩阵形式如下:

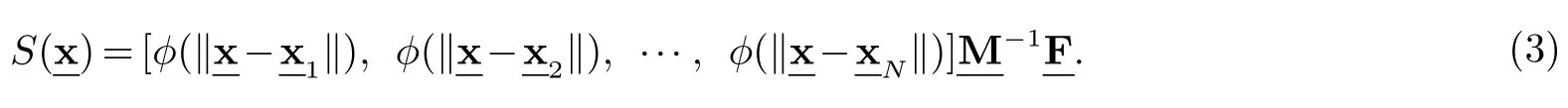
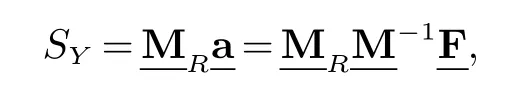
2 基于MQ-RBF插值的间断检测方法

图像边缘是以图像局部特性的不连续性形式出现的.图像边缘检测在图像处理中是众多科学家感兴趣的课题,经典的检测方法是给出一个满足初始条件的微分方程模型,使得初始曲线向着图像边缘移动.当到达图像边缘时,曲线停止移动,这样就找到了图像的边缘.数值拟合该微分方程常用的方法是水平集方法,该方法的优点是在不知道检测边缘的前提下可以很自然地检测到不同拓扑结构的图像边缘.但其缺点是,求解高维问题会耗费大量的计算时间.而MQ-RBF边缘检测方法在检测高维问题时,使用维数分裂的方法，这将在某种程度上降低求解的复杂度.

2.1 MQ函数发展历程

MQ函数是Hardy于1968年提出的一种径向基函数.Hardy[22]总结了MQ函数自发现以来20年间所取得的研究成果,并列举了MQ函数在众多工程方面的应用.他将MQ函数的发展历程分为以下三个阶段:

•1968-1972年是研究MQ函数基本方法的时期,在这一时期得到的比较实用的方法包括配置模型、最小二乘模型、密切模型、区域分解等;

•1972-1979年主要表现在MQ函数在各方面的广泛应用,如在大地测量学、地球物理学、测绘学、摄影测量学、遥感与信号处理、数字地形模型、水文学、地质学与采矿等领域的应用;

•1980-1988年是研究MQ-B函数及其数学论证的时期.

在这期间里,虽然MQ函数在微分方程和积分方程中有一定的应用,但主要还是将MQ函数用于插值方面.Franke在文[2]中指出:就精度、稳定性、有效性、内存需要及易于实现而言,MQ函数在所有的29种散乱数据插值格式中是最好的.对于MQ函数及其逆MQ函数[23]研究了奇Buhmann数维Euclidean空间上插值的收敛阶,得到如下结果:当n>3为奇数时,它们的收敛阶分别为n+1和n−1阶.此外他进一步研究了MQ函数单变量拟插值的收敛性问题.与此同时,他和Micchem[24]也研究了多变量整数网格上MQ函数的局部化性质的改进问题.这在某种程度上丰富了MQ函数的理论.

2.2 迭代自适应间断检测方法

图像的边缘检测是图像处理中一项重要的预处理技术,是图像分析与识别的重要环节,也是处理许多复杂问题的关键,被广泛应用于图像轮廓、特征的提取和纹理分析等方面.边缘检测法的种类有很多,如微分算子法、样板匹配法、小波检测法、神经网络法等.目前常用的高效边缘检测方法包括傅里叶共轭和增强共轭边缘检测方法,它们分别由Gelb[25]和Tadmor[26]提出,这两种边缘检测方法都是基于傅里叶方法,并已经成功地应用于多种领域.以下将给出一种更加精确的边缘检测方法:基于MQ-RBF的ε迭代自适应方法[26]

.虽然RBF方法在数值逼近间断的地方会产生吉布斯现象[27],但可以利用该现象构造一种更加精确的边缘检测方法.迭代自适应MQ-RBF方法主要利用扩散系数不同的增长率,来确定间断点的所在位置.即对于中心点总数N,如果形参固定,那么扩散系数的绝对值在间断或间断附近会达到局部最大并且会随着N的增大呈指数增长.同时,在远离间断的地方,扩散系数的量级成指数级衰减;但是如果在间断或间断附近把形式参数赋空,扩散系数的量级将成线性衰减.这种迭代自适应MQ-RBF方法应用于边缘检测的成功之处在于扩散系数的增长率随着形式参数自适应的变化而显著变化,并且无论所考虑的区域连续与否,扩散系数的变化都能容易的检测到.在Jung[26,28]等人的研究工作基础上,以一维和二维间断问题为例来研究自适应边缘检测方法.对于二维问题,采用维数分裂的方法进行求解,此方法的优点是程序简单易实现,计算效率高.

2.2.1 一维迭代自适应RBF方法

ε迭代自适应方法的关键思想是:固定网格形式和N,MQ-RBF逼近的精度仅依赖于εj.理论上,当被逼近函数f(x)足够光滑时,随着εj的增加会得到好的收敛结果.但事实上,εj并不能随意增大.当εj=0时,局部MQ-RBF就转变为分片线性函数φj=|x−xj|.但当所有的εj=0时,由于所有的基函数都是线性的,所以整体的逼近也呈线性收敛.由此,局部ε自适应方法可简单概括为:若中心点xj为间断点,则εj=0;若中心点xj为非间断点,则εj0.

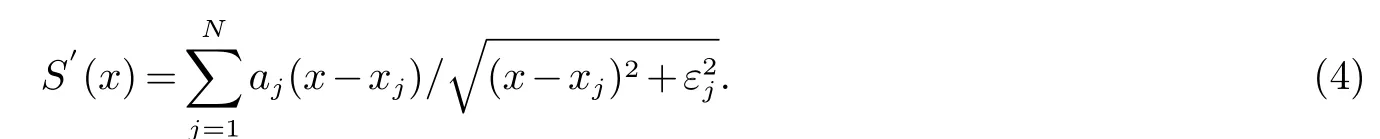
特别地,若εj=0,在xi=xj,i=1,···,N时,令

现定义如下集合:

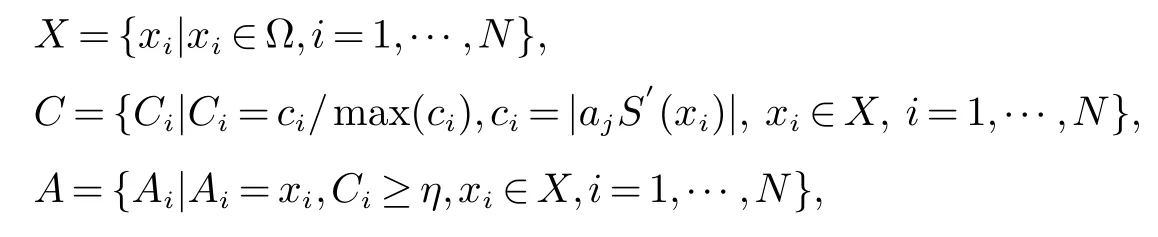
这里η是给定的已知数.

给定:{εi},1>η>0,δ>0,aold

步骤1:由(2)和(5)式计算a,

步骤2:求得间断点集合

步骤3:更新ε,即：若则εi=0;若为初始值,重新计算C;

步骤4:如果更新aold,重复步骤1→步骤3.

需要提及的是,对于集合C,可以只用一阶导数或扩散系数(Ci=|ai|,i=1,···,N)来作为步骤2的判断标准,但是,在某些特殊情况下，这二者都没有步骤1里定义的判断标准效果好.

现给出一个含有多个间断点的一维算例,在区间[−1,1]上其间断函数f(x)和间断点[f]如下:

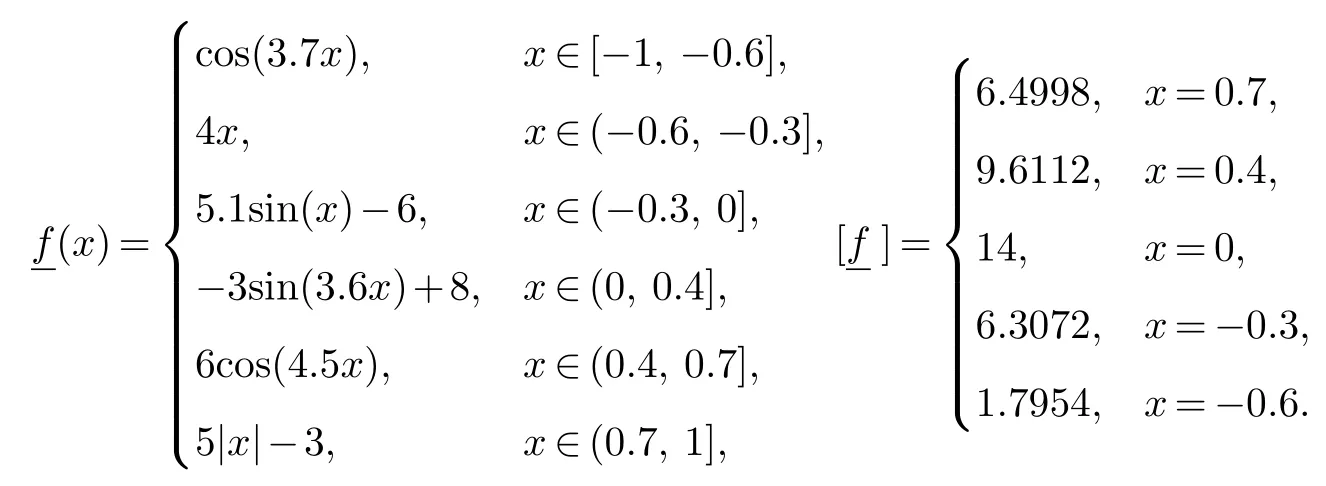
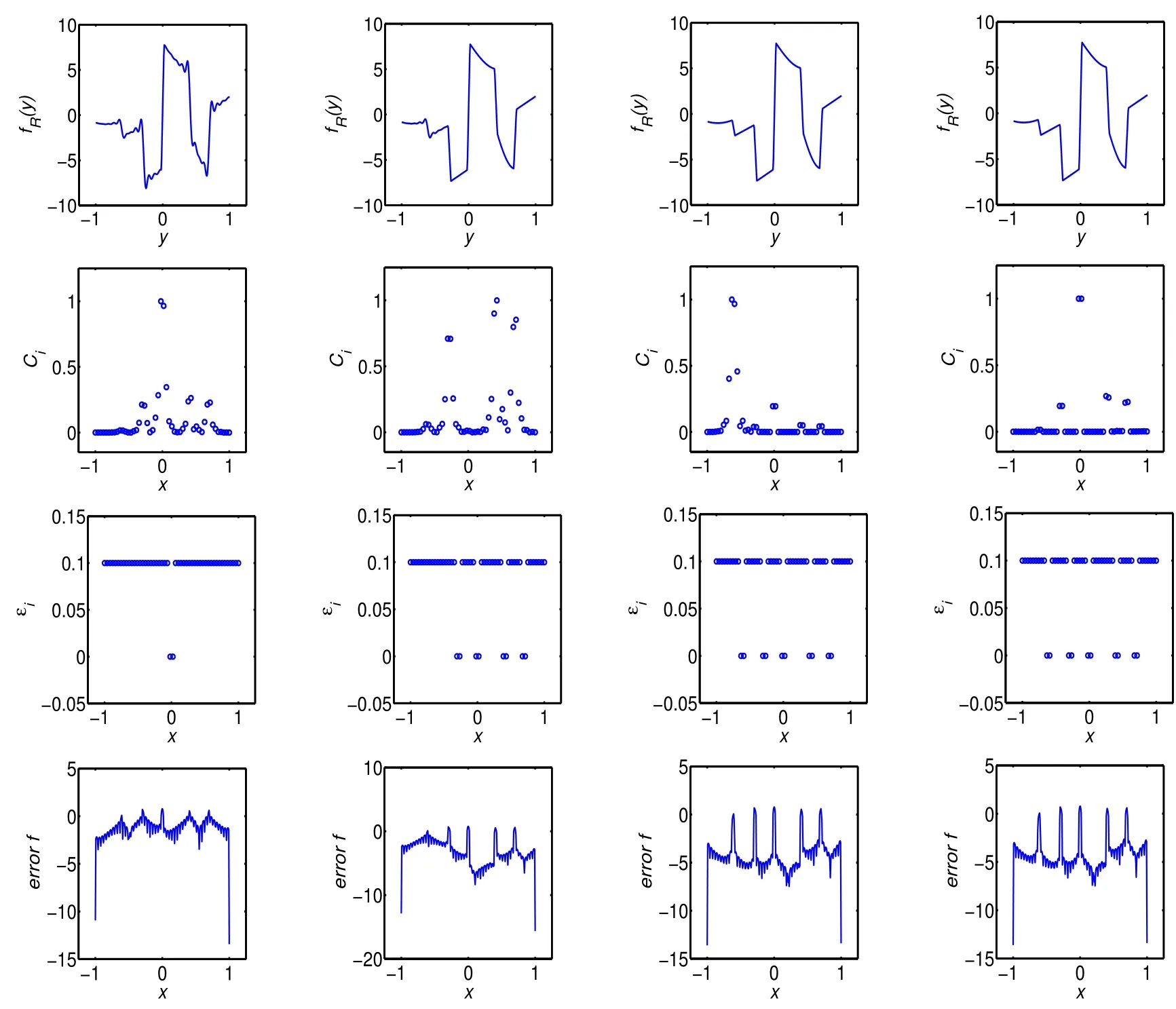
图1 第一行是重构函数(y),第二行是判断标准C,第三行是形式参数ε,第四行是error =log10|(y)−(x)|

2.2.2 二维迭代自适应RBF方法

由于整体方法需要求解的系数矩阵规模较大且为满阵的方程组,因此,对于二维问题将采用维数分裂的方法来降低求解的规模,并提高计算效率.由文献[26]得到,对于固定的ε=0.1,迭代自适应方法稳定条件就是求解的最小区域xmin和中心点个数N需满足关系式:xmin≈0.006N−0.1.

以下将给出一些二维的算例,并且所有例子中取δ=1e-10,形式参数的初值都为ε=0.1.图2中,从左到右依次给出一个大小为500×500的钟表表盘的图片以及x方向检测的边缘图,y方向检测的边缘图和两个方向合起来检测的结果,其中η=0.1,ε=0.1.图3中原图片大小为600×600,η=0.1.图4中原图片大小为465×500,η=0.03.图5中原图片大小为540×540,η=0.1.图6中原图片大小为554×435,η=0.1.图7中原图片大小为906×700,η=0.02.

需要说明的是,由于原始图片本身有一些噪点,就是较弱的间断点,所以在这些二维的例子中,其检测出来的边缘轮廓会有一些噪点,这是很正常的情况而不是说迭代自适应方法不好;相反地说明用这个方法来检测间断点是非常精确的.

图2 左图是原图,往右依次为x,y方向检测边缘图和两个方向合起来检测的轮廓图

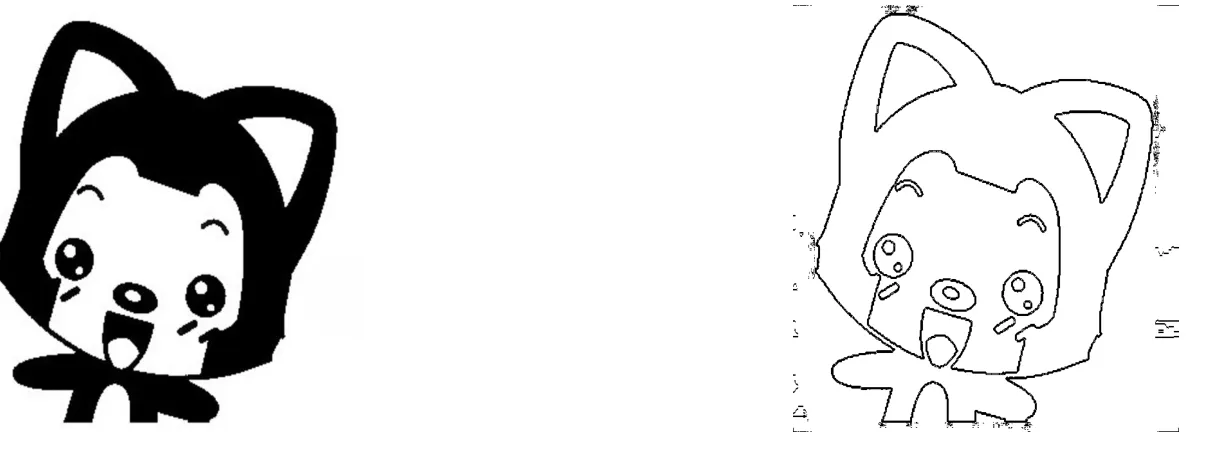
图3 左图是一个阿狸的原图,右图是检测的轮廓图

图4 左图是一个苹果的原图,右图是检测的轮廓图

图5 左图是一个二维码的原图,右图是检测的轮廓图

图6 左图是一个指纹的原图,右图是检测的轮廓图

图7 左图是一个闹钟的原图,右图是检测的轮廓图

3 结论

通过本文的研究发现,RBF方法具有不依赖于网格剖分、表达形式简单、易于编程、计算效率和精度较高等优点.但是,所要求解方程组的系数矩阵是满阵,故对其进行求解时需花费较长时间,并且该方法在理论分析上不及有限差分方法、有限元方法等那么完善,但这反而为今后的研究工作提供了一个方向.在今后的工作中，将会尝试研究高维情况下不同类型的RBF方法(如高斯型RBF,逆MQ-RBF等)在间断检测上的应用.由于MQ-RBF产生的插值矩阵是满阵,因此寻求一些高效的数值计算方法是很有必要的,如区域分解、并行计算等方法.此外,RBF方法是一种无网格法,故用它求解偏微分方程和反问题也将是今后研究的重点.

致谢本文撰写的顺利完成,作者要感谢美国Brown大学的曾维新教授和中国海洋大学的高振教授在相关题材方面进行的讨论和合作,并寄予了许多宝贵的建议和精心的指导,谨在此表示衷心的感谢.