设置分级例题，提升教学成效——以“网格中的锐角三角函数”为例

☉江苏省苏州市工业园区星海实验中学　杨　洪

设置分级例题，提升教学成效
——以“网格中的锐角三角函数”为例

☉江苏省苏州市工业园区星海实验中学杨洪

一、写在前面

复习课因没有现成的教材，给了教师很大的自主设计教学的空间.一线老师往往会打破复习课的章节限制，重新整合教学内容，并对教学方法和教学流程进行相应调整.复习课的设计，既要完成前一阶段知识的“继承”，又要为下一阶段的学习铺垫.因此，很多老师特别重视复习载体——例题的教学设计，想着法子提高例题的教学效益.近期，笔者就复习课的例题设计也进行了一番尝试，用分级设置的例题引导学生展开复习，取得了较好的成效.现结合“网格中的锐角三角函数”专题复习的例题及教学设计谈一些个人的感悟，希望能给您的教学带来一些启示.

二、例题设计及分析

1.背景分析

“锐角三角函数”主要涉及三个函数：正弦（sin）、余弦（cos）和正切（tan）.这三个函数的定义是本章教学的重点，我们不仅要让学生学会求直角三角形中某一锐角的这三个函数值，还要让他们学会建构直角三角形求函数值.这节课的设计正是基于这样的教学需求，通过一组以“网格”背景的函数求值题，将所学的锐角三角函数作为解题目标蕴含其中，力求在学生解答中渗透转化思想和模型思想.

2.例题解析

例1（A级题）如图1，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA= _________.

解析：在图1中，△ABC的三个顶点均在格点上，所以∠ABC=90°.所以.根据小正方形的边长为1，可得AB=3，BC=4，所以tan

图1

图2

例2（B级题）如图2，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上，则cosA=______.

解析：如图2，作CD⊥直线AB，D为垂足（说明：原图中没有辅助线和点D，下同）.所以，AD=4，CD=2，由勾股定理得

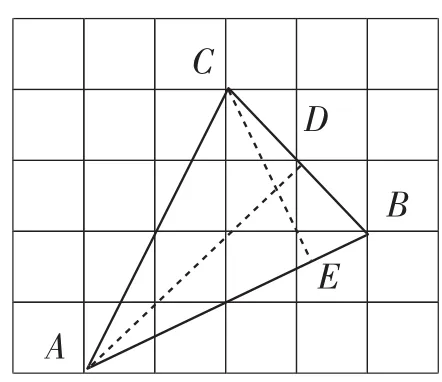
图3

例3（C级题）如图3，网格中的每个小正方形的边长都是1，△ABC的每个顶点都在网格的交点处，则sinA= _______.

解析：如图3，作AD⊥BC于点D，CE⊥AB于点E，由勾股定理得.根据“面积法”易得BC·AD=AB·CE.所以

简析：本节课的复习主题是“网格中的锐角三角函数”，这是近几年中考中常见的试题.为了帮助学生形成解题策略，教者围绕这一主题，共设计了三道例题.例1是一道“看看就能给出答案”的题目，难度较小，适合所有同学解答，所以设为“A级题”；例2，需要建构直角三角形，为了求∠A的余弦，还需先应用勾股定理求出AC的长，难度较例1有所增加，适合班级中等及以上学生解答，所以设为“B级题”；例3的考点明显增加，在正确添加辅助线后，解题还要用到勾股定理和三角形的面积公式等知识，难度较大，适合班级中学有余力的同学解答，设为“C级题”.这三道例题，梯度清晰，不同的难度适合不同的学生解答.教师设计例题时，不仅按照难度递增呈现例题，还将适做人群在题号后的括号内进行了标注，这样的设计是人性化的，给学生的自主选择提供了极大的便利.

3.教学设计

学生通读三道例题，在理清题目条件和结论的基础上，按照“就高不就低”的原则（“高”指难度较大的例题，下同）从中选择一道解答，完成后分别到课前已经划定的A级题、B级题和C级题交流区域交流，要求不仅要交流解题的结果，还要交流解题思路获得的过程，以及用到的数学知识和思想方法.在完成同级交流后，再回到原来的学习小组进行“异级交流”，主要是由解答“高位题”的同学进行“低位题”的思路分析及过程指导.最后，教师组织全班交流，主要交流“建构（应用）直角三角形求解”的共性解法和B、C级题求解时用到的转化思想.

简析：教者设计的教学流程，紧贴学生的认知需求，在个性学习上做足了文章.首先是审题，这是学生解题的基本能力，我们平常教学就应该高度重视.在这节复习课上，给学生一段时间单独审题，既符合常态教学需求，也是教者后续教学活动的基础.在这一时段内，学生可以详细解读每一题的条件与结论，并努力在脑海中初步搭建条件与结论关联的通道，形成预估“解题报告”，为下面的选题提供“理论支撑”.这种多道同类题的同步解读，不仅训练了学生的审题技能，还培养了学生分析问题的能力.接下来就是选题，教者预设了“就高不就低”的选题原则，意在逼着学生选择难度较大的例题解答.我们相信，每一名学生都会站在自己所能达到的高度上认真审视给出的这几道例题，理性地做出选择.事实上，学生最终做出的选择是“正态”分布的，绝大多数同学会选择B级题，选择A级题的是班级中数学基础薄弱的学生，而选择C级题的正是班级中那些“高手”.有了这种选题的经历，很多学生都能较为顺利地给出问题的答案，所以，接下来的自主解答显得十分顺利，耗时很少.在学生解题结束后，教者通过互动交流的方式让学生展示了自己的结果和获得结果的过程.整个交流分三个层次，“同级交流”是第一层次，重在结果与思路的交流；“异级交流”是第二层次，意在释疑解惑和共同进步；最后是教师引导下的“全班交流”，突出了例题的共性解法的建构和数学思想方法的提取.就整个教学设计来看，学生始终是教学的主体，教师几乎没有一丝干扰，预设的例题和流程很好地引导学生展开了课堂学习，知识的获得与应用在这样一种极其自然的状态下进行，取得较好的教学效果也就在情理之中了.

三、几点感悟

1.以考点整合为抓手，实现教学例题真分级

例题的分层、分级设置是一件好事，很多老师都想去做，而且一直在努力找到例题设置的一些策略.在对例题分级进行了一段时间的尝试后，笔者发现知识点的适度增减，可以调整例题的难度.据此，在例题分级的过程中，我们可以以考点整合为抓手，实现教学例题真分级.具体做法是先选择一道较为成熟的试题作为分级例题的“原型”，然后深入剖析“原型”所涉及的知识点，这里所说的知识点既包含一些显性知识，如解题所需要的数学的基础知识和基本技能，也包括隐含在题目或解题过程中的隐性知识，如渗透于题目中的数学思想和解题所必备的基本活动经验.通过对这些知识点的适度增减形成新的选题目标或改题方向，最终形成以“原型”为中心（即B级题）的三级题目.要说明的是，知识点的增减不应是数学上的加减，应是在原有知识点基础上的有效渗透或适度删除，要让学生审题与解题看不出人为设置的痕迹.以本文中的三道题目为例，例2是笔者进行分级的“原型”，网格中的三角形是一个普通三角形，其中一条边恰好是网格中水平方向的“格点线段”（说明：在教学中，我们把以格点为端点与网格水平线平行或垂直的线段叫做格点线段），另两条边则不是“格点线段”，所以本题不仅要建构直角三角形，还要用勾股定理求出直角三角形的边长，以上是对原型的分析，既包含了知识点的分析，也包含了解题思路和解题方法的分析.接下来，我们可以通过增加或减少“格点线段”来调整题目的难度，从而让例题自然分级.比如，例1中“格点线段”有两条，所求的正切值只与这两条线段有关，所以难度降了下来；例3中没有了“格点线段”，不仅要建构直角三角形，还要想办法求出与所要求的正弦值有关的两条线段的长度，三角形面积公式的引入让题目难度增加了不少，将这道题编排为C级题是合乎情理的.

2.以分级例题为载体，推进分层教学轻着陆

《义务教育数学课程标准（2011年版）》提出：数学课程“要面向全体学生，适应学生个性发展”，这就要求我们的教学不仅要让每一名学生都学有所获，还要让“不同的人在数学上得到不同发展”.因此，我们的课堂教学不仅要“求同”，还要“存异”.当所有学生“齐步走”的时候，我们还应关注那些学有余力的同学，要为他们准备一些难度稍大的学习资料，让他们既能“吃得了”，又能“吃得饱”.分层教学，正是基于这样的教学主张之上生成的教学方式，本文所述的例题分级及教学应用，恰到好处地将分层教学的理念转化成了教学行为.因此，课前，我们要围绕教学主线设计好分级例题，将课时核心有机渗透到题组中；课上，我们可以通过学生的自主选择与解答这些分级例题，让教学自然分层；课后，我们还可以为学生设计分层练习，让分级例题的教学效应进一步延续.通过分级例题的有效应用，分层教学也就会“落地生根”，真正落在实处.在笔者设计的“网格中的锐角三角函数”专题复习课上，正是有了课前的精心设计和课上的精准实施，加之与例题配套的练习的设置，学生真正开展了“有差异地学习”，几乎每一名学生的学习积极性都被调动起来，学习成效十分显著，他们在课上能自主选择并进行解答，交流气氛热烈，交流成果丰硕，在课后能准确地选择自己能够解答的“高”级练习，作业的正确率很高.

3.以教学适用为目标，确保分层设例不偏向

分层教学，分层是教学的一种辅助形式，我们最终实施的是教学内容和教学对象适度分级的教学.所以，设计的例题都应以教学适用为前提.例题的分级设置，应遵循人人受益的原则.我们的分级绝不是建立在“盲目地选择高难度的题目，或者是无休止地降低例题的难度”基础之上的.分级例题的设置，不仅要保证不同级别之间例题的梯度，还要保证选出的或者改编的例题紧扣本节课的课堂教学主线，切实为教师的教和学生的学服务.为了能让学生“有差异地学习”，我们设计的例题必须是难易适中，能让学生开展数学学习.难度过大的例题，不仅基础薄弱的同学不能解答，有时甚至连成绩优秀的同学同样不能求解，这样的例题编排使得每一名学生都没有收获，显然是不适宜的；例题过于容易，也是不妥的，三级例题之间差距不大，一方面学生选择困难，不利于培养学生学习数学的自信心，另一方面，题目过于容易，不太容易调动优秀学生学习的积极性，不利于培养其思维的深刻性.因此，想要让分级例题适用于教学，我们就应充分关注学情，将学情分析与目标设定和例题设计同步，力求例题设计符合学情，符合目标要求.以本文中的三道例题为例，在设计之初，笔者详细分析了近几年的中考现状和本单元的教学目标制定了教学目标，与此同步，笔者还对本班学生这一版块知识的掌握与应用情况进行了分析，摸清了基础薄弱学生和优秀学生的认知现状.有了这样的基础，笔者选择了一道中等难度的试题作为例题原型，通过叠加和删减知识点，在教学主线之上合理地渗透进一些与本单元关联较大的知识，让例题的难度有效增减，实现了紧贴教学目标和学情的有效分层.接下来的教学应用中，教者更是以适用为目标，对学生中出现的符合本课教学目标的生成进行了积极处理，而那些与本节课关联不大的问题则淡化处理，关注的是课时核心，成就的是方法积累和素养提升！

1.陈开金.网格上的问题［J］.上海中学数学，2007（5）.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.