基于热模态分析的主轴热误差鲁棒性建模*

杨昌祥，王立坚，何 川，卢红星，杨建国

（1.贵阳险峰机床有限责任公司，贵州黔南布依苗族自治州 550601；2.上海交通大学机械与动力工程学院，上海 200240）

基于热模态分析的主轴热误差鲁棒性建模*

杨昌祥1，王立坚1，何 川1，卢红星2，杨建国2

（1.贵阳险峰机床有限责任公司，贵州黔南布依苗族自治州 550601；2.上海交通大学机械与动力工程学院，上海 200240）

为提高数控机床的加工精度，针对主轴热误差提出一种基于热模态分析的鲁棒性建模方法。类比动力学模态分析，利用有限元分析方法对机床主轴进行热模态分析，获得主轴热模态时间常数和温度场，并以此为依据确定温度传感器在主轴上的安装位置，利用回归分析方法建立热误差数学模型。频率敏感性仿真实验结果表明，误差模型在不同热流输入频率下均具有非常好的拟合效果。最后通过实验验证了所提出建模方法的鲁棒性和准确性。

数控机床；热误差；误差建模；热模态；鲁棒性

0　引言

随着各行业对高端精密零件、设备需求的不断增长，制造业及相关研究领域认识到了提高机床精度的重要性。机床精度直接决定所加工零件的尺寸和表面精度，而热误差［1-2］是影响机床精度的一个重要因素，占机床总误差的50%左右。主轴热误差是机床热误差的重要组成部分，由于主轴内、外热源影响导致其结构发生热变形，进而造成所加工零件尺寸误差超出允许范围。

过去几十年，国内外研究人员对主轴热误差进行了大量的研究。杨建国等［3］通过对简化的一维主轴模型分析得出一种温度测点优化布置策略，使主轴热伸长与温度读数值之间呈近似线性关系，减少了温度传感器的使用，提高了测量效率。Kim.B［4］针对主轴热漂移误差提出一种状态空间模型，并在一台高精密车床上进行了补偿实验，取得了良好的效果。此外，杨漪［5］、蔄靖宇［6］、闫嘉钰［7］、吴雄彪［8］等也在机床热误差方面做了相关理论分析和实验探索。

然而，误差模型的精度和鲁棒性［9］仍是热误差补偿技术广泛推广的最大障碍。本文基于热模态分析，从热变形的本质出发，类比动力学振动模态分析，利用有限元方法对机床主轴进行热模态分析，在分析结果的基础上提出一种经济有效的温度传感器布置策略和高鲁棒性的误差模型，通过多元线性回归方法建立热误差模型。频率敏感性有限元仿真结果表明该误差模型具有良好的鲁棒性。将该模型应用于一台卧式车床进行主轴热误差鲁棒性预测实验，结果证明该建模方法对不同热流输入具有良好鲁棒性和预测精度。

1　热模态分析方法

利用有限元方法对机床进行动力学振动模态分析，早已成为机床设计制造过程中获得机床动力学特性的重要手段。有限元分析也被很多研究人员用于机床热误差的研究［10］，以便加强传统经验建模方法。然而，对机床进行热模态分析［11］以掌握机床热时间常数和模态形状也是十分重要的，目前，利用有限元方法进行机床主轴热变形的本质分析方面的研究还很少。

为了进行热模态分析，需要得到主轴温度场分布，首先求解热传递微分方程：

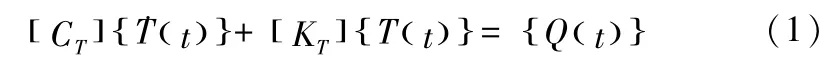
式中：［CT］是热容量矩阵，｛T（t）｝ 是节点温度向量，［KT］是热导量矩阵，｛Q（t）｝ 是节点热负载向量。

式（1）的特征方程为：

在模态分析中，特征向量矩阵 ［ΦT］可以作为解耦式的一个传递矩阵，把物理温度矩阵T（t）转换为模态温度矩阵｛θ（t）｝：

根据微分方程的性质，由式（1）、（2）和（3）可得到：

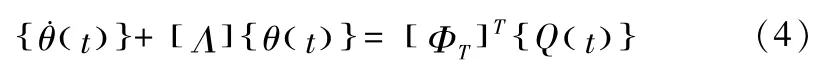
令，［ΦT］T｛Q（t）｝=｛ξ（t）｝ ，其中｛ξ（t）｝代表模态热负载向量。如果施加一个阶跃热流输入到机床主轴上，可得式（4）的解为：

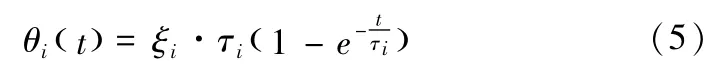
式中：θi（t）为第i个热模态的温度场分布。

由于主轴的热负载变化也大致可以看作一系列阶跃输入的组合。这样，主轴总体的温度响应就可以看作这些热模态的叠加。这种热模态分析的优点是整个热变形过程可以利用几个主要热模态来表示。每个热模态的权重定义为：

式中：ξi和τi分别为每种模式的热负载和时间常数。权重的大小决定了每种模态的比重。通常，其中几个模态占据总权重的一大部分，其余的热模态影响可以忽略不计。

1.1主轴热变形的有限元仿真

为进行主轴热模态分析，通常先建立主轴简化模型，然后进行有限元分析［12］。为方便描述，对主轴热误差进行简化处理，如图1所示，典型的主轴热变形包括三个误差量，分别为膨胀量ε，倾斜量δ，以及倾角θ。

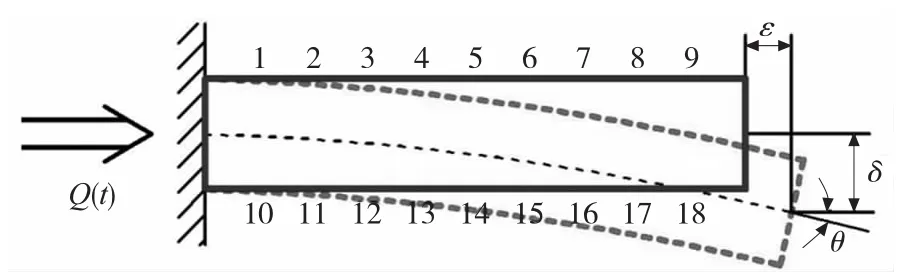
图1　简化主轴热漂移模式

在仿真中，假设热量输入Q（t）位于固定端，热误差产生的一端自由。热传递主要发生在机床部件接触表面以及与环境之间。假设上表面的热传递系数20W/m2K，下表面的热传递系数为100W/m2K，其它材料参数如表1所示。

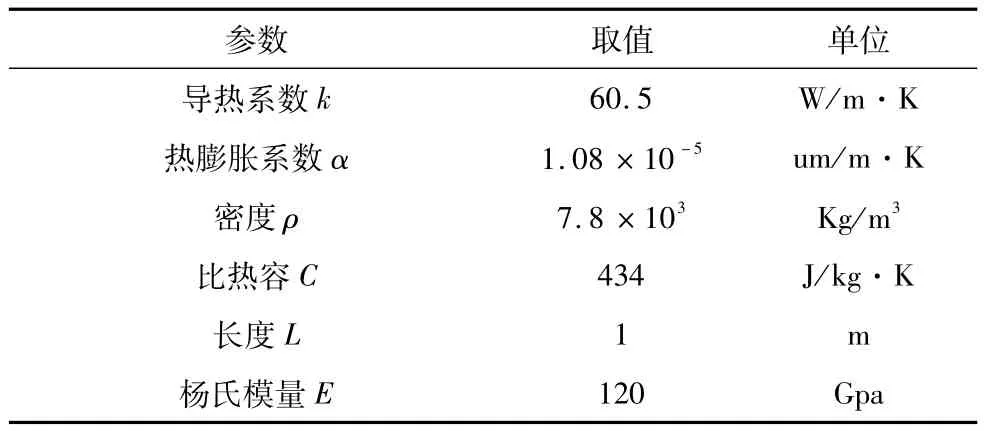
表1　主轴特性参数

1.2基于热模态分析的温度传感器布置

通过有限元分析结果发现，前四个热模态的权重系数大小逐次递减，四个权重之和占总比重的90%以上，说明前四个热模态在热变形的过程中起到了主导作用。前四个热模态的时间常数和温度场如图2所示。

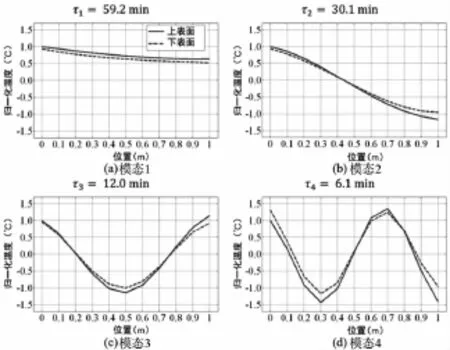
图2　前四个热模态的温度场

类似于振动模态分析，温度传感器位置的安放要遵循下面两条准则：

（1）接近主要温度场的最值处；

（2）接近主要热源。

根据这一策略，通过对前四个热模态权重分布以及温度场分布情况分析，可以确定温度传感器的安装位置。在仿真过程中，选择放置3个传感器进行温度测量，分别位于位置1，5，10处，如图3所示。

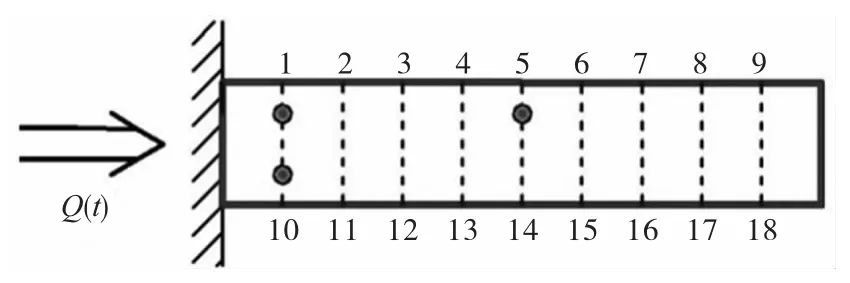
图3　温度传感器的布置

2　热误差鲁棒性建模

多元线性回归模型利用最小二乘法来拟合数值，相比于其它建模方法，比如人工神经网络，具有结构简单，逼近精度高，外推性好等特点，所以被广泛用来描述热误差的变化规律。但是多元线性回归模型受多重共线性问题的影响，选择建模时的温度变量合理与否，一直是影响热误差模型鲁棒性的重要因素。

以主轴热伸长ε为例，其形式如下：

式中：T1，T2，T3代表测点温度变量，β0，β1，β2，β3为回归系数，e为随机误差。基于最小二乘法原理利用数学软件可以方便计算出回归系数。

该建模方法的鲁棒性可通过频率敏感性仿真实验来验证。频率敏感性的重要性主要在于机床操作和环境条件的周期，这两个量会导致热负载按照特定的周期而改变。

由于生产安排和环境条件等，机床主轴的热源变化规律，通常服从一定的周期性。据此特点，在仿真实验中，在不同的频率热流输入下检测了频率的敏感性。一次热流的周期为20min，如图4a，该热流被用来训练模型。然后用两个传统的热流输入来验证模型，周期分别为40min和10min，如图4b和4c所示。设初始状态简化的主轴有限元模型的初始温度为20℃，分别施加图4所示的热流输入，进行有限元仿真，仿真结果如图5所示。

从图5中可以很明显看出，得到的热误差模型对频率变化具有很强的鲁棒性。仿真实验证明基于热模态分析所确定的温度传感器位置能够获取整个热变形的本质。显然，通过热模态分析可以有效地控制温度传感器的使用数量，从而降低误差建模的复杂程度，同时提高温度测量实验的效率。

图4　频率敏感性实验的热流输入

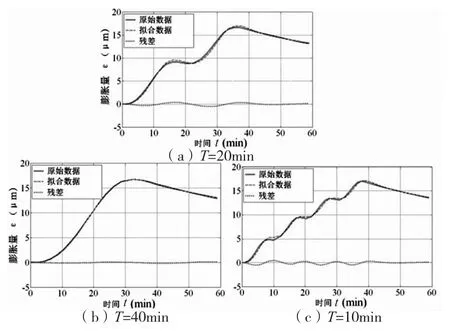
图5　频率敏感性实验结果

3　实验验证

所提出的热误差建模方法通过在一个卧式机床的主轴上进行验证。图6显示实验装置，其中主轴通过一个交流电机控制。通过一个电容传感器测量主轴的热膨胀。基于简单机床结构件热伸长理论，将3个温度传感器安装在主轴上来收集温度数据。

图6　主轴热伸长测试的实验装置

首先，进行训练实验1来得到主轴的热误差模型。按照图7a所示的主轴速度将机床运行70min，按一定的采样频率读取三个温度传感器的读数，温度记录结果如图7b所示。五个电容传感器实时记录机床主轴的热变形。利用多元线性回归分析方法建立变形量与温度变量之间的数学模型。为方便描述，以主轴热伸长为例，实验结果如图8所示，可以看出多元回归建模方法能够很好地拟合测量数据，残差在±1μm以内。

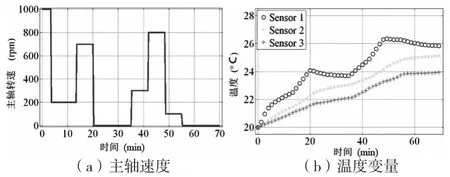
图7　实验1的实验结果

图8　实验1的测量和建模结果

为了验证所得热误差模型的鲁棒性，设计两组验证实验，分别为实验2和实验3。如图9所示，改变主轴速度变化模式，实验2中使热机时间缩短50%，实验总时间缩短为50min，实验3中使热机时间增加50%，实验总时间增加到90min。通过改变主轴实际运转时间，使主轴受热情况发生变化。两次实验均实时采集测点的温度数据和主轴热伸长量。根据所测温度和实验1中得到的主轴热伸长误差模型，分别对实验2和实验3进行误差预测。测量值和预测得到的误差如图9所示。

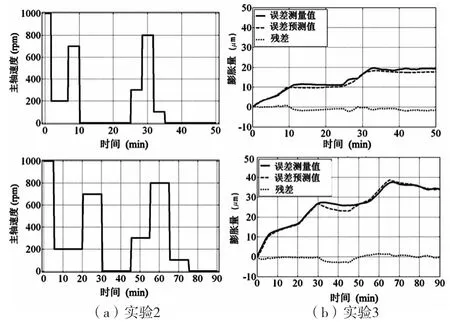
图9　主轴速度对于鲁棒性验证测量和预测误差

从实验结果中可以看出，绝大部分的热误差都可以通过得到的热误差模型来预测，两次实验的残差都在±2μm，证明所提出的建模方法具有很强的鲁棒性。从图中可以看出，在冷却阶段测量值和预测值的偏差相对于热机阶段较大。一方面，这一现象是由于主轴热源不仅仅来自于交流电机，还来自于主轴轴承的摩擦。另一方面，由于仿真阶段主轴的有限元模型过于简化，没有考虑主轴的内部结构造成的。所以，使用更详细的有限元模型进行热模态分析，同时增加温度传感器数量来获得更多的温度信息，是提高数控机床主轴热误差模型鲁棒性的一种有效途径。

4　结论

基于热模态分析，提出一种热误差鲁棒性建模方法，利用有限元分析来获取主轴主要热模态时间常数，权重系数及其温度场，类比振动模态分析，提出一种温度传感器的布置策略，既能较准确反映主轴热变形的本质，又能有效地控制温度传感器的使用数量，降低误差建模的复杂程度。通过多元线性回归分析的方法建立主轴热误差模型，结合温度传感器布置位置，进行频率敏感性有限元仿真实验，结果证明该误差模型具有良好的鲁棒性。

实验数据证明了建模方法的有效性和鲁棒性。本文基于热模态分析从热变形的本质出发，提出了一种经济有效的温度传感器布置策略和高鲁棒性误差模型，不仅可以节省大量的时间和精力在热误差模型的训练过程，而且保证了热误差模型的精度和鲁棒性，为后续误差补偿提供了良好的基础。

［1］Ramesh R，Mannan M，Poo A.Error compensation in machine tools—a review：Part II：thermal errors［J］.International Journal of Machine Tools and Manufacture，2000，40（9）：1257-84.

［2］Mayr J，Jedrzejewski J，Uhlmann E，et al.Thermal issues in machine tools［J］.Cirp Annals-Manufacturing Technology，2012，61（2）：771-91.

［3］杨建国，王秀山，赵海涛.机床热误差模型中温度测点布置［C］.重庆：2005年中国机械工程学会年会，2005.

［4］Kim BS，Song YC，Park CH.Robust Thermal Error Modeling and Compensation for a Nano Level Thermal Drift in a High Precision Lathe［J］.International Journal of Precision Engineering and Manufacturing，2011，12（4）：657-61.

［5］杨漪，姚晓栋，杨建国，等.基于主成分分析与BP神经网络相结合的机床主轴热漂移误差建模［J］.上海交通大学学报，2013，47（5）：750-753，759.

［6］蔄靖宇，赵海涛，杨建国.车削中心主轴箱热误差仿真及特性分析［J］.中国机械工程，2009，20（18）：2182-2186.

［7］闫嘉钰，杨建国.数控机床热误差的最优线性组合建模［J］.上海交通大学学报，2009，43（4）：633-637.

［8］吴雄彪，姚鑫骅，傅建中.基于贝叶斯网络的数控机床热误差建模［J］.中国机械工程，2009，20（3）：293-296.

［9］Yuan J，Ni J.The real-time error compensation technique for CNC machining systems［J］.Mechatronics，1998，8（4）：359-380.

［10］Weck M，McKeown P，Bonse R，Herbst U.Reduction and compensation of thermal errors in machine tools［J］.Cirp Annals-Manufacturing Technology，1995，44（2）：589-598.

［11］Yang J，Yuan J，Ni J.Thermal error mode analysis and robust modeling for error compensation on a CNC turning center［J］.International Journal of Machine Tools and Manufacture，1999，39（9）：1367-1381.

［12］Zhao HT，Yang JG，Shen JH.Simulation of thermal behavior of a CNC machine tool spindle［J］.International Journal of Machine Tools&Manufacture，2007，47（6）：1003-1010.

（编辑 赵蓉）

Robust Thermal Error Modeling for CNC Machine Tools Spindle Based the Thermal Mode Analysis

YANG Chang-xiang1，WANG Li-jian1，HE Chuan1，LU Hong-xing2，YANG Jian-guo2
（1.Guiyang Xian Feng Machine Tool Co.，Ltd.，Qiannan Buyei and Miao Autonomous Prefecture Guizhou 550601，China；2.School of Mechanical Engineering，Shanghai Jiao Tong University，Shanghai200240，China）

In order to improve the machining accuracy of NC machine tools，a robust thermal error modeling strategy based on the thermal mode analysis is presented.Finite element analysis is utilized to determine the time constant，weight and temperature field of each thermal mode.On this foundation，temperature sensors are placed to capture the dominant thermal modes of thermal deformation process.Multiple linear regression models are employed to describe thermal errors of spindle.Numerical simulation is conducted to verify the robustness of the thermal error models in terms of frequency sensitivity.At last，practical experiments are carried out and the results proved that the proposed modeling method is robust and effective.

CNC machine tool；thermal error；error modeling；thermal mode analysis；robustness

TH161；TG506

A

1001-2265（2015）02-0090-04 DOI：10.13462/j.cnki.mmtamt.2015.02.025

2014-06-06

国家自然科学基金项目（51275305）；国家科技重大专项课题（2011ZX04015-031）

杨昌祥（1969—），男，苗族，贵州惠水县人，贵阳险峰机床有限责任公司高级工程师，从事机床设计与制造，（E-mail）ycxxfmtw@126. com；通讯作者：卢红星（1990—），男，河南周口人，上海交通大学博士研究生，研究方向为精密加工与测试，（E-mail）lu_hx1990@126. com。