分段式永磁直线同步电机磁阻力分析及优化设计*

杨俊友，王 欢，白殿春，朴海顺

（沈阳工业大学电气工程学院，沈阳 110870）

分段式永磁直线同步电机磁阻力分析及优化设计*

杨俊友，王 欢，白殿春，朴海顺

（沈阳工业大学电气工程学院，沈阳 110870）

磁阻力是引起永磁直线同步电机（PMLSM）推力波动的主要原因，降低了电机的推力特性。文章分析了12槽11极PMLSM磁阻力形成机理及周期性分布规律，并采用有限元法论证了一种能消除推力波动的分段式初级铁芯的方法。分析结果表明，具有三个铁芯模块组合初级的直线电机能有效减小磁阻力。最后对分段式PMLSM磁阻力进行综合分析，为PMLSM本体设计和伺服系统设计提供参考。

永磁直线同步电机；磁阻力；有限元；分段式初级铁芯

0　引言

永磁直线同步电机（PMLSM）作为现代高速精密直线进给伺服系统驱动装置的最佳选择，具有推力密度大、电气时间常数小、损耗低、响应速度快等特点，广泛应用于精密机床中，具有很高的加速度、超高的刚度、高定位精度及平滑的无差运动［1］。永磁直线同步电机在静态情况下，由于动子铁芯两端开断，存在着明显的端部效应力；由于电机铁芯开槽，产生了齿槽效应力。端部效应力和齿槽效应力合称为磁阻力，是PMLSM推力波动的主要原因，是伺服控制系统扰动的主要来源。因此降低磁阻力能有效改善PMLSM伺服性能［2］。

文献［3］通过优化动子铁芯长度和端部开倒角减少了端部效应力，但忽略了齿槽效应的影响。文献［4］利用辅助齿有效降低了磁阻力波动，但是辅助齿增加了加工的难度。文献［5］对齿槽效应和端部效应进行了定性分析，并且提出了减小定位力的措施，但是缺乏具体的建模和数值分析。文献［6］对PMLSM空载时的齿槽效应力和端部效应力进行了研究，提出了单独分析计算左端和右端效应力，最终合成优化的设计方法，并采用傅里叶级数非线性回归分析法进行短初级优化设计，但在优化时未计及齿槽效应所引起的推力波动。文献［7］在PMLSM的次级轭铁的横向方向，安装两排永磁体，并将两排永磁体沿着运动方向错开一定距离以减小推力波动，采有限元法进行了分析和验证，但并没有涉及到一排永磁体，初级分段的设计方式。文献［8］提出采用单元电机段间移相的措施进一步削弱永磁直线电机推力波动的两单元段间移相设计方法，但并没有推广到N段，具有一定局限性。文献［9］提出分段式铁芯初级结构，利用数学公式推出铁芯距离与极距的关系，并进行有限元验证，但没有考虑到由于分段移相绕组所施加激励的变化，没有分析结果是否为最优。

本文首先分析PMLSM磁阻力产生原因，采用有限元法单独分析齿槽力和端部力对磁阻力的影响，提出了一种能有效降低推力波动的分段式初级铁芯方案，为PMLSM本体优化和伺服系统设计提供参考。

1　12槽11极PM LSM磁阻力分析

齿槽力和端部力共同构成了PMLSM的磁阻力，为了便于研究两者对推力波动影响大小，分别对其进行有限元分析：如图1a所示，PMLSM次级不开槽，此时只考虑端部效应对磁阻力的影响。图1b假设初级铁芯无限长，此时只考虑齿槽效应对磁阻力的影响［10］。通过有限元分析，分别得到齿槽力和端部力的分布情况，如图2所示。

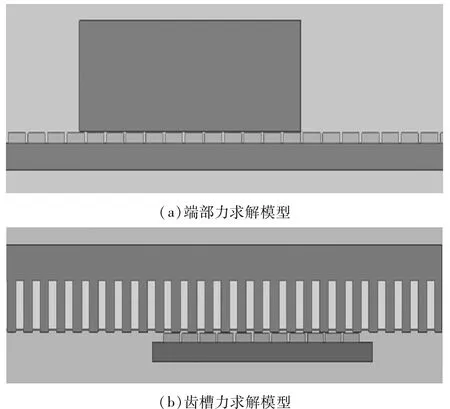
图1　磁阻力产生原理分析

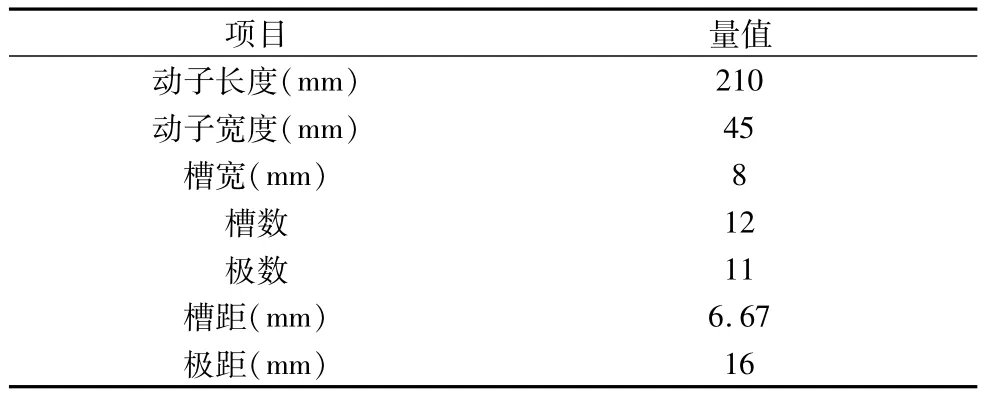
表1　原型机结构尺寸

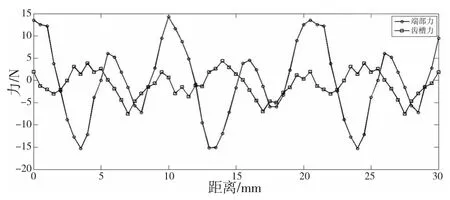
图2　端部力与齿槽力

图2结果表明端部力为磁阻力波动的主要部分，其周期为极距τ=16mm，齿槽力远小于端部力，其周期为7mm，接近于一个齿距。原型机尺寸如表1所示。

2　分段式初级铁芯模型

本文提出一种分段式初级铁芯结构（图3），进一步降低磁阻力波动大小，假设将k个初级铁芯单元沿次级纵向移动L=nτ+mτ/k距离，均匀排列，构成具有相同结构尺寸和电参数的组合式铁芯的初级，其中m与k互为质数，τ为极距，n为整数，且保证铁芯间隙大于τ［9］。其有限元分析取n=13，m=1，k=3。

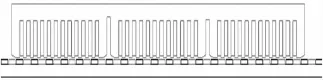
图3　三段式初级铁芯有限元模型

3　推力波动谐波分析

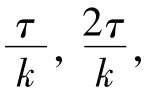
以上分析表明，导致稳态静推力波动的各个成分，如齿槽效应力、端部效应力和纹波推力均为以极距τ为周期的函数［7］，因此以Fourier级数形式表述作用在第1个铁芯模块推力波动函数为［9］：

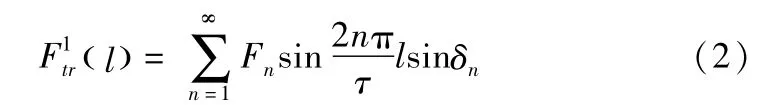
式中，l为第一个铁芯模块移动距离，Fn为n阶谐波频率的幅值，δn为初始相角，与选取X轴方向坐标原点相对应。则利用叠加定理可推出k个铁芯模块组合初级的推力波动为：

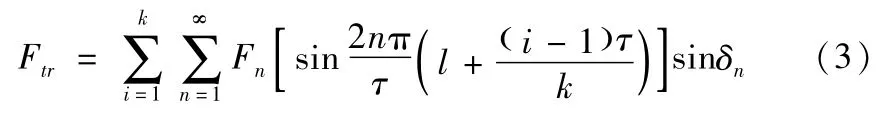
通过对式（3）进一步简化可得到k模块组合铁芯的推力波动Ftr计算式：

式（4）表明，推力波动中2、3阶等低阶分量均被消去，只包含k阶及其倍频分量。

将以上分析结果推广到更为一般的情况，将k个铁芯模块相互间按机械位置相差mτ/k排布，若k与m互质，其推力波动计算式与铁芯间机械位置相差τ/k布置时推力波动计算式相同，此时消除推力波动的效果等同于本文所推导结果；若m与k有公约数q，低阶频率成分均被消去，磁阻力构成成分只包含k/q阶及其倍频。

4　有限元分析

为了验证上面数学推导的结果，进行有限元分析，对相邻铁芯之间A相绕组的距离L进行有限元分析，取n=13，即L=210mm～220mm，结果如图4所示。

图4　不同铁芯距离磁阻力分布情况

利用有限元分析不同铁芯距离对磁阻力的影响，如图4所示，当L=211时得到最小化的磁阻力波动幅值为5.3N，原型机为12.7N下降了7.4N。根据数学公式L=nτ+mτ/k其中n=13，m=1，k=3得当L= 213.3时磁阻力波动幅值最小，而实际有限元分析为L=211时磁阻力波动幅值最小。因此通过公式计算所得到的L值并不是最优结果，还需要以其为基础，再进行局部优化，求得最佳L值。

图5　单段铁芯与三段铁芯磁阻力分布

图5对比分析单段初级铁芯与三段初级铁芯磁阻力分布情况，单段初级铁芯磁阻力峰峰值与平均推力的比值为12.95%（24.69N），优化之后三段初级铁芯磁阻力峰峰值与其平均推力比值为1.5%（9.7N），显著降低。

5　绕组的对称特性

本文对三段初级铁芯进行推力波动有限元分析，与单铁芯不同之处在于绕组如何分配三相电流，（按槽在图3中从左到右的顺序）：，其中绕组间机械位置角差2π/3。

为了得到三段式初级铁芯直线电机的推力最大值，分别对三段绕组单独通三相正弦交流电。有限元分析发现，若三段绕组通以相同相位三相正弦交流电，第二段铁芯会产生与另两段铁芯相反方向的推力，无法形成稳定推力。通过ansoft有限元分析发现，分别使每段电机感应电势相位相同，改变第二段铁芯初级绕组三相正弦交流电初始相位φ，能够解决此问题，得到稳定推力，如图7所示。

图6和图7中给出了单模块和组合模块电机的稳态推力比较曲线。组合电机的平均推力为654.40N，是原型电机190.29N的3.44倍。三段式初级铁芯PMLSM的平均推力不仅没有降低，反而略有增加。为便于比较分析推力波动的改善情况，将对推力波动值与对应电机平均推力的比值进行比较分析。如图7和图6所示，组合电机推力波动幅值由原型电机的22.75%（43.29N）下降到2.33%（15.28N），下降了8.7倍。

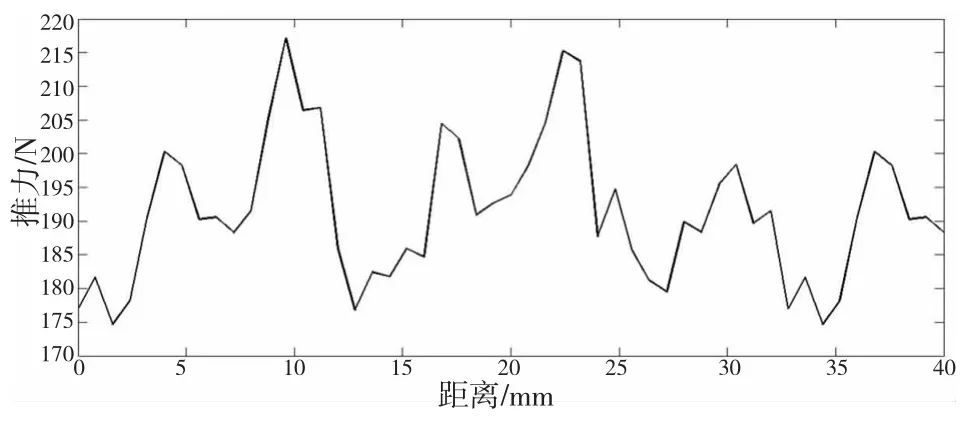
图6　原型机推力分布

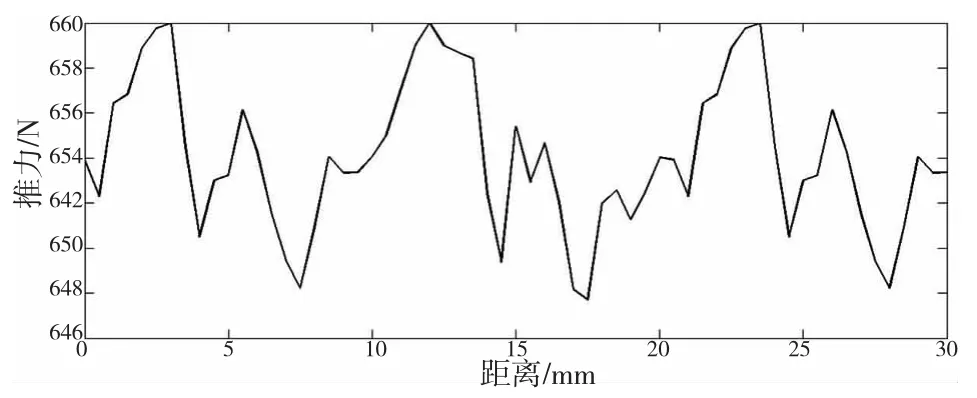
图7　优化后三段式初级铁芯推力分布

对单段初级铁芯原型电机和三段初级铁芯组合电机推力波动进行谐波成分分析，结果如图8所示。在单铁芯原型电机中，推力波动主要构成成分为2、3、5、7阶谐波，其来源为静磁阻力。对组合电机推力波动有影响的谐波成分为3阶和5阶，其中由静磁阻力波动产生的3阶谐波幅值最大，同时由电磁脉动产生的5阶谐波也有较大的幅值。谐波分析验证了组合铁芯方法消除低阶谐波的效果。在单铁芯原型电机中，对推力波动有影响的谐波成分为2、3谐波。三模块组合后，2、3阶谐波成分显著减小，残留为3阶谐波及其倍频，组合后总推力波动幅值大幅降低。

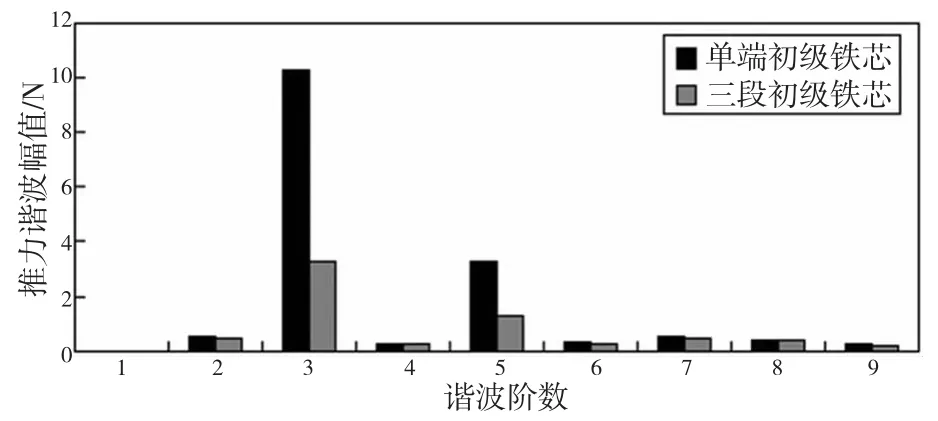
图8　单段初级铁芯与三段初级铁芯谐波分析

6　结论

本文首先阐述了PMLSM磁阻力的产生原理，分析对比齿槽力和端部力对磁阻力的影响，并采用有限元法论证了一种能消除静推力波动的分段式初级铁芯模型，优化初级铁芯移动距离，获得最大推力。分析结果表明，具有三个初级铁芯模块的直线电机能有效的减小磁阻力及推力波动，并且得到了三个铁芯模块绕组分配规律以及如何控制激励的初始相位以得到最大推力，最后通过综合分析，得到了分段式［参考文献］

初级铁芯结构间距离的基本确定方法，为PMLSM本体设计提供有效的依据。

［1］夏加宽，刘班，王成元.段间移相永磁直线同步电机的建模与自抗扰控制［J］.组合机床与自动化加工技术，2009（12）：61-65.

［2］M.S.Hosseini，S.Vaez-Zadeh，Modeling and analysis of linear synchronous motors in high speed maglev vehicles［J］.IEEE Transactions on Magnetics，2010，44（7）：2656-2658.

［3］Lee D，Zhou J，Jeong S.Optimal design of auxiliary-teeth to reduce detent force by end-effect inmoving coil type PMLSM［J］.Field Computation，2006，38（2）：4244-4250.

［4］Seok-Myeong，Jang-Young Choi，Han-Wook Cho，etal.Experimentand characteristic analysis of disk type PMLSM with Halbach Array［J］.IEEE Transactionson Magnetics，2005，41（10）：3817-3819.

［5］潘开林，傅建中，陈子辰.永磁直线同步电机的磁阻力分析及其优化［J］.浙江大学学报（工学版），2005（10）：169-174.

［6］Liu Chengying，Wang Hao，Zhang Zhijing，et al.Research on thrust characteristics in permanent magnet linear synchronous motor based on analysis of nonlinear inductance［J］. Proceedings of the CSEE，2011，31（30）：69-75.

［7］Yong-Jae Kim，Suk-seung Hwang.Cogging force reduction of a stationary discontinuous armature PMLSM by magnet segmentation［J］.IEEE Transactions on Magnetics，2009，45（6）：2750-2753.

［8］夏加宽.高精度永磁直线电机端部效应推力波动及补偿策略研究［D］.沈阳：沈阳工业大学，2006.

［9］程元雄.永磁同步直线电机推力波动的优化设计研究［D］.武汉：华中科技大学，2010.

［10］Yu-WuZhu，Dae-HyunKoo，Yun-HyunCho.Detent force minimization of permanent magnet linear synchronous motor by means of two different methods［J］.IEEE Transactions on Magnetics，2008，44（11）：4345-4346.

（编辑 赵蓉）

Detent Force Analysis and Optimization Design of Permanent M agnet Linear Synchronous Motor

YANG Jun-you，WANG Huan，BAI Dian-chun，PIAO Hai-shun
（School of Electrical Engineering，Shenyang University of Technology，Shenyang 110870，China）

The detent force is composed of cogging force and end effect force in permanent magnet linear synchronous motor（PMLSM）.The detent force is a major factor of thrust ripple of PMLSM，which deteriorates the motion control characteristics.This paper analyzed the forming principle and periodic distribution of 12-slot11-pole PMLSM's cogging force and demonstrates a kind of segmented core primary method which can eliminate static thrust fluctuation with finite element method（FEM）.Analysis results show that linear motor with three core module combination primary can effectively reduce detent force.Comprehensive analysis of the segmented core primary method was adopted to provide

for design of PMLSM servo system.

permanent magnet linear synchronous motor（PMLSM）；finite element method（FEM）；detent force；segmented core primary

TH166；TG659

A

1001-2265（2015）02-0071-03 DOI：10.13462/j.cnki.mmtamt.2015.02.020

2014-05-09

国家自然科学基金项目（51075281）；教育部高等学校博士学科点专项资助项目（20112102110002）；辽宁省高等学校创新团队资助项目（LT2010081）

杨俊友（1963—），男，天津人，沈阳工业大学教授，博士，博士生导师，主要从事特种电机及其控制、风力发电系统与控制等研究，（E-mail）junyouyang@yahoo.com。