谐波齿轮传动共轭齿廓求解方法的研究*

王敏杰，范元勋，祖 莉

（南京理工大学机械工程学院，南京 210094）

谐波齿轮传动共轭齿廓求解方法的研究*

王敏杰，范元勋，祖 莉

（南京理工大学机械工程学院，南京 210094）

在谐波传动啮合原理的基础上，给出一种共轭齿廓求解方法。利用Abaqus求解柔轮的初变形，提取齿圈中截面中性层节点的径向变形位移和切向变形位移，结合Matlab曲线拟合工具箱，以子项为正弦函数的多项式作为拟合函数，求取柔轮的变形函数。以此代替理论变形函数，完成柔轮单齿啮入啮出的运动仿真，对其运动轨迹的包络曲线进行最小二乘拟合，得到刚轮齿廓曲线。结果表明：基于包络理论，结合有限元法和运动仿真，对于求解共轭齿廓是可行的，为谐波齿轮传动的设计提供了参考。

有限元法；变形函数；运动仿真；包络

0　引言

谐波齿轮传动共轭齿廓的设计，是在已知柔轮齿廓曲线和原始曲线的基础上，通过对理论啮合方程的求解，得到刚轮齿廓曲线。求解过程中，柔轮变形函数的选取会直接影响啮合状态，误差过大易导致轮齿啮合干涉、啮合侧隙不均匀等现象的出现。但是，由于谐波齿轮传动的复杂性，柔轮的变形也呈现出复杂的变化规律［1］。目前，国内主要采用椭圆凸轮波发生器，将其装入柔轮后，柔轮齿圈中截面的理论变形函数是在柔轮中线不伸长、母线仍为直线、不考虑轮齿影响等相关假设的基础上，由弹性壳体理论求解而得。推导过程涉及椭圆积分运算［2］，方程形式较为复杂，这为共轭齿廓的求解增加了难度。

文献［3］以渐开线齿啮式输出谐波传动为研究对象，利用有限元分析和傅里叶函数拟合得到的负载变形函数对共轭齿廓进行修正，这种方法为共轭齿廓求解过程中变形函数的选取提供了新的思路。利用有限元分析软件ABAQUS以及Matlab曲线拟合工具箱求取柔轮空载变形函数，以此代替理论变形函数，结合运动仿真，给出一种谐波齿轮传动共轭齿廓的求解方法，为谐波齿轮传动的设计提供了参考。

1　共轭齿廓的基本理论

以谐波齿轮传动用于减速作为讨论基础，即刚轮固定，波发生器输入，柔轮输出。原始曲线指的是位于受载平面内柔轮的中线在波发生器作用下形成的弹性变形曲线［4］。图1为求解共轭齿廓的几何模型：与刚轮相固连的全局坐标系CG（xG，yG）是固定坐标系，其坐标原点OG与谐波传动装置的回转中心重合，纵轴yG是刚轮齿槽的对称线；局部坐标系CR（xR，yR）与柔轮相固连，其坐标原点OR是轮齿的对称线与柔轮原始曲线SR的交点，纵轴yR是柔轮轮齿齿廓的对称线；局部坐标系C0（x0，y0）与波发生器相固连，其坐标原点O0与全局坐标系原点OG重合，纵轴y0与波发生器的长轴重合。

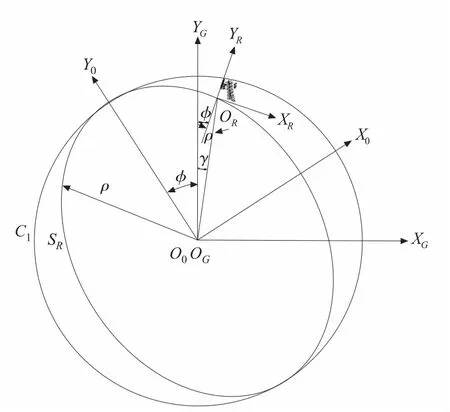
图1　求解共轭齿廓的几何模型

按照包络理论，得到与柔轮齿廓曲线相共轭的刚轮齿廓表达式［4］为：

式（1）中，ρ为柔轮原始曲线的极半径；φ为刚轮固定时，相应CR与CG两坐标系Y轴的夹角；φ为波发生器的转角；γ为柔轮转角；U/z1为广义传动比，U为柔轮变形波数，z1为柔轮齿数；ω为径向变形位移；υ为切向变形位移；μ为柔轮轮齿偏转角。

由式（1）可知，若能已知径向变形函数ω以及切向变形函数υ，便可代入共轭齿廓方程求解得到刚轮齿廓曲线。而对于式（1）的求解是关于隐函数偏导求解，推导过程较为复杂，若能结合运动仿真，可使求解过程变得简便。

2　柔轮初变形的有限元分析

柔轮的初变形是指将波发生器装入柔轮后，不加负载的条件下，由于凸轮的作用，柔轮不可避免发生的变形。以常用的环状刚轮、杯形柔轮和椭圆凸轮波发生器构成的双圆弧谐波齿轮传动为例，对共轭齿廓的求解方法作详细阐述。柔轮基本齿廓曲线为公切线式双圆弧齿轮基本齿廓，与ΓOCT15023-69标准［5］下的齿廓曲线一致，基本参数包括模数m=0.5mm，柔轮齿数Zr=200，刚轮齿数Zg=202，传动比i=100，柔轮径向变形系数ω*=1，齿圈壁厚δ=0.9mm。

2.1有限元模型的建立

在Pro/E中建立柔轮和波发生器的几何模型后，保存为x_t格式后导入Abaqus中。柔轮材料选用35CrMnSiA，对其进行调制和表面氮化处理，弹性模量为209GPa，泊松比为0.295；波发生器材料为45，弹性模量为209GPa，泊松比为0.269。考虑到较多的接触区域，选取单元类型为8节点线性减缩积分C3D8R，并采用沙漏控制。

对柔轮建模时，为保证有限元法的求解精度，考虑轮齿对变形的影响［6］，保留柔轮齿圈，并采用全模型代替对称模型。网格划分前，需从杯顶开始，用以轴线为法线的平面进行分割，先将齿圈前沿分割出来，然后将齿圈分为三个部分，前沿倒角、中间齿圈、后沿倒角；再将筒体和杯底分割开，通过扫掠分割将杯底倒角独立出来。

对波发生器的装配过程进行分析时，由于没有涉及波发生器的转动，可忽略椭圆凸轮和柔性轴承之间的滚动摩擦以及柔性轴承滚珠分布的影响，将波发生器组件简化为一个刚性薄壁环，其外轮廓为以柔性轴承厚度等距包络形成的曲线［7］。几何建模时，将波发生器分为上下两个半椭圆，上半部分下移距离ω，下半部分上移距离ω，其中，ω为最大径向变形量。柔轮的有限元模型如图2a所示，波发生器有限元模型如图2b所示。

图2　有限元分析模型

2.2定义约束条件

（1）分别指定波发生器上下两个半椭圆各自的参考点，限制波发生器的所有自由度，将其约束为刚体，给定上半凸轮参考点向上的位移和下半凸轮参考点向下的位移，其值为ω，以模拟波发生器装入柔轮的过程［8］；

（2）限制柔轮的轴向位移；

（3）将波发生器外表面和柔轮内表面定义为接触区域，在定义接触对时，以波发生器外表面为目标面，柔轮内表面为接触面。

2.3有限元结果分析

柔轮的径向变形云图如图3所示，切向变形云图如图4所示。提取柔轮齿圈中截面中性层的径向变形数值、切向变形数值，将其与理论变形函数进行比较。其最大径向变形值出现在波发生器长轴方向，极值为0.553mm，大于理论值0.5mm；在波发生器短轴杯口处，径向位移为负，最大值为-0.557mm，大于理论值-0.5mm。其最大切向变形值出现在与波发生器长轴成正负45°方向杯口处，极值为0.293mm，大于理论值0.25 mm。

图3　柔轮径向变形云图

图4　柔轮切向变形云图

进一步分析可知，柔轮杯口由于变形而将波发生器包裹其中，解释了谐波传动工作过程中柔性轴承外圈前沿出现磨损破坏的原因［9］。另一方面，由于实际工作过程中柔轮杯底的限制，其变形沿轴向并不均匀，使得柔轮母线发生倾斜，导致柔轮内壁与波发生器外轮廓并未出现理论所假设的紧密贴合［8］。因此，有限元结果与理论变形并不一致，其更接近于柔轮的实际变形。

3　拟合变形函数

结合谐波齿轮传动的啮合特征，以柔轮齿圈中截面中性层圆周方向上节点的径向位移和切向位移作为拟合变形函数的数据源。由于径向变形和切向变形是周期变化的，而且其函数是可积的，因此须用可积的周期函数对数据进行逼近拟合。基于此考虑，选取子项为正弦函数的多项式作为拟合函数。

Matlab拟合工具箱cftool中提供9项正弦函数的线性组合，需对各种结果的拟合误差进行分析，进而选择最优的拟合函数。拟合函数的优劣评判因素有误差平方和SSE、均方根误差RMSE、调整自由度复相关系数Adjusted R-square以及复相关系数R-square。前两个因素越接近0，后两个因素越接近1，说明离散数据和拟合函数的拟合度越高［3］。径向变形函数和切向变形函数可用统一的表达式表示：

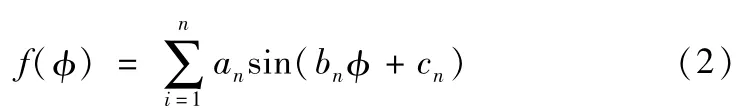
式（2）中，an、bn、cn为拟合函数的系数。

经过对9种不同拟合方式的比较，得到径向变形的最佳拟合结果如表1所示，最大拟合误差为0.00107mm，是最大径向变形量的1/517，对求解结果的影响可以忽略，拟合函数的选取是可靠的。拟合函数与理论径向变形函数的比较及其误差曲线如图5所示，最大误差为0.053mm。

表1　有限元径向变形函数拟合结果

图5　径向变形拟合与误差曲线

同理，切向变形的最佳拟合结果如表2所示，最大拟合误差为0.00053mm，是最大切向变形量的1/553，可以忽略。拟合函数与理论切向变形函数的比较及其误差曲线如图6所示，最大误差为0.043mm。

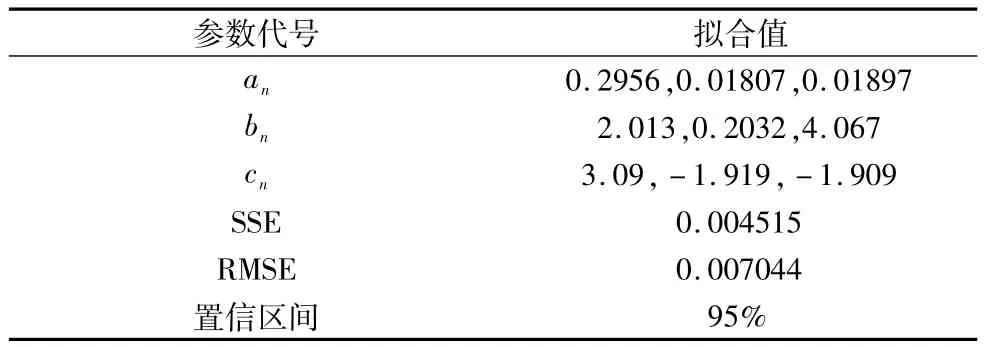
表2　有限元切向变形函数拟合结果

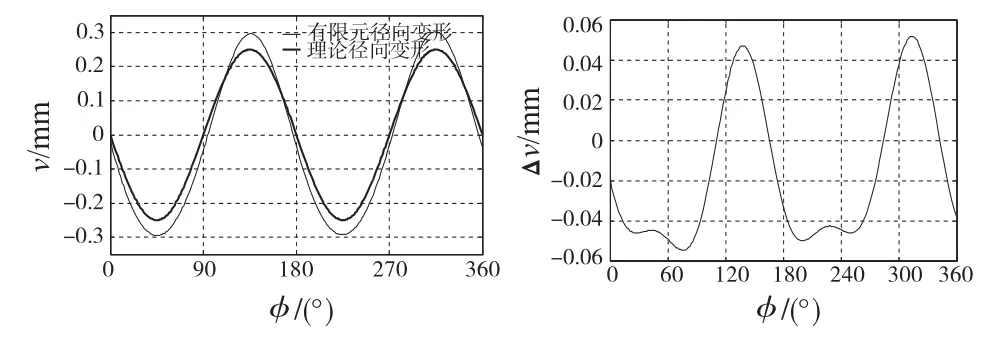
图6　切向变形拟合与误差曲线

由以上分析可知，拟合函数的方程形式较为简单，拟合误差可以忽略不计，以此作为变形函数是可靠的。

4　运动轨迹的包络

将得到的拟合函数表达式代入啮合方程式（1），利用柔轮坐标系到刚轮坐标系的坐标变换矩阵，确定柔轮齿廓在刚轮坐标系的映射，以柔轮单齿的一个完整啮入啮出过程为基础，获得柔轮轮齿相对刚轮轮齿的运动轨迹，再对这一系列的曲线族进行数学包络［10］。利用Matlab编程，可求得柔轮运动轨迹的包络如图7所示。

图7　柔轮运动轨迹的包络

运用包络法对共轭齿廓进行求解时，往往出现包络点超出工作范围，这种数学形式的包络齿廓工艺上无法实现。因此，求解刚轮齿廓时，需考虑刚轮的制造工艺和品质要求。本例中，利用最小二乘法，选择圆弧-直线-圆弧拟合刚轮齿廓曲线上的离散点。为了保证刚轮齿廓曲线的拟合精度，需比较刚轮齿廓点和拟合圆弧的偏差［4］，求得拟合齿形与理论齿形的最大误差为0.00869μm，平均误差为0.00576μm。参考小模数渐开线圆柱齿轮齿形公差，最大误差相当于6级精度齿形公差的1/1381。因此，从工程意义上讲，刚轮采用圆弧-直线-圆弧的齿廓是合理的。需要说明的是，所求齿廓曲线仅是刚轮参与啮合的工作段齿廓，求取全齿廓时还须考虑过渡圆角、柔轮齿顶与刚轮齿根应留有顶隙等因素。

5　结论

（1）利用Abaqus求解柔轮的初变形，选取子项为正弦函数的多项式作为拟合函数，对柔轮齿圈中截面中性层的径向变形位移和切向变形位移进行拟合。由分析可知，拟合函数的拟合误差可忽略不计，变形函数的选取是可靠的。

（2）用拟合函数替代理论变形函数，基于包络理论，结合有限元法和运动仿真的数值解法，对于求解谐波齿轮传动共轭齿廓是可行的。

但是，所求共轭齿廓的啮合性能和精度指标还需通过实验进一步验证。

［1］阳培，王长路.谐波齿轮传动中柔轮初始变形力研究［J］.机械强度，2006，28（8）：78-82.

［2］辛洪兵.双圆弧谐波齿轮传动基本齿廓设计［J］.中国机械工程，2011，22（6）：656-662.

［3］董惠敏，张春懋.齿啮式谐波传动柔轮负载变形函数及齿形修正的研究［J］.机械传动，2011，35（7）：7-11.

［4］沈允文，叶庆泰.谐波齿轮传动的理论和设计［M］.北京：机械工业出版社，1985.

［5］卢贤攒.圆弧齿轮啮合原理［M］.北京：机械工业出版社，2003.

［6］储著金，谭晶.谐波传动中柔轮轮齿对柔轮变形的影响分析［J］.机械传动，2014，38（2）：129-132.

［7］Han Xuefeng，Bai Yang，Li Ming，Jiang Hongguang.Alternating stress dynamics analysis of harmonic gear flexible wheel［C］.International Conference on Electrical Insulating Materials and Electrical Engineering.2012，5：487-493.

［8］齐书学.谐波传动柔轮结构参数优化与整机动态仿真［D］.大连：大连理工大学，2009.

［9］Chen X X，Lin S Z，Xing J Z.The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive［J］.Mechanism and Machine Theory.2014，73：1-24.

［10］范元勋，王华坤，宋德锋.谐波齿轮传动共轭齿廓的计算机数值模拟研究［J］.南京理工大学学报，2002，26（4）：389-392.

（编辑 赵蓉）

Study on Solving Method for Conjugate Profiles of Harmonic Gear Drive

WANG Min-jie，FAN Yuan-xun，ZU li
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

Based on meshing principle of harmonic drive，a method of solving conjugate profiles is proposed.The initial deformation of flexspline could be figured out by Abaqus.Radial deformation and tangential deformation of the deformed points on neutral surface of middle section would be collected.Combined with curve fitting toolbox of Matlab and taking sum of sin functions as fitting function，deformation function of the flexspline were got.Substitute theoretical deformation function with it，and after completing the motion simulation of engaging-in and engaging-out for a single tooth，fit the envelope curve of the flexspline' s motion trail by least square method.The tooth profile of rigid spline would be worked out.The result shows that based on the envelope theory，combined with finite element method and motion simulation，conjugate profiles can be worked out and it can provide reference for design of harmonic gear drive.

finite element method；deformation function；motion simulation；envelope

TH132.43；TG506

A

1001-2265（2015）02-0013-04 DOI：10.13462/j.cnki.mmtamt.2015.02.004

2014-05-29

国家自然科学基金项目（51105206）；中央高校自主科研专项计划项目（30920130121015）

王敏杰（1990—），男，江苏淮安人，南京理工大学硕士研究生，研究方向为机械设计及理论，（E-mail）wangm jie2008@163.com。