基于ADAMS的航发精锻叶片边缘砂带磨削机构的优化设计*
詹 飞,张明德,张卫青,徐浩驰
(重庆理工大学机械工程学院,重庆 400054)
基于ADAMS的航发精锻叶片边缘砂带磨削机构的优化设计*
詹 飞,张明德,张卫青,徐浩驰
(重庆理工大学机械工程学院,重庆 400054)
设计一种新型的砂带磨削机构,该机构采用伺服电机、螺母丝杆与弹簧的结构,实现了航发精锻叶片边缘的浮动磨削加工。基于Adams仿真软件平台,对新型砂带磨削机构进行仿真,得到接触力曲线。根据接触力曲线,采用均匀实验设计方法,优化砂带磨削机构的弹簧刚度系数、弹簧阻尼系数与导杆阻尼系数,优化后的新型砂带磨削机构的接触力稳定时间降低到0.1s内,且其接触力最大振动幅值较小,证明了文章设计的新型砂带磨削机构具有较好的接触力动态响应特性。
叶片边缘;砂带磨削;ADAMS;运动仿真
0 引言
航发叶片是航空发动机的关键零部件,其加工质量的优劣决定着航空发动机效率的高低。航发叶片边缘具有复杂的结构特点与较高的加工工艺要求,目前国内航空发动机精锻叶片进排气边缘通常采用普通铣床切边后进行手工打磨成型的加工方法。这种加工方法容易导致叶片进排气边缘的加工精度较低、加工后的叶片边缘型面一致性较差以及叶片边缘与叶身转接不圆滑等问题,从而增加叶片加工报废率[1]。
针对上述问题,本文设计了一种新型的砂带浮动磨削机构,采用伺服电机驱动螺母丝杆,以获得快速的输入激励响应,用弹簧连接丝杆与导杆,实现浮动磨削。利用机械动力学仿真软件ADAMS建立砂带磨削机构的动力学仿真模型,进行仿真分析,优化浮动磨削机构关键参数,提高接触力的动态响应特性。
1 航发叶片边缘结构特点及磨削加工工艺要求
本文以某航空发动机精锻叶片为例,如图1所示,分析航发叶片边缘的结构特点及磨削加工工艺要求。
叶片边缘结构特点:航发精锻叶片由榫头、叶身、阻尼台组成,叶片叶身长85.4mm,弦宽约58.9mm;叶片进排气边缘弧半径R的范围为0.18mm~0.67mm;叶身曲面由16个截面给定,每个截面由叶背、叶盆两条样条曲线和叶片进排气边圆弧光顺拼接而成。
叶片边缘加工工艺要求:航发精锻叶片边缘通常采用普通铣床切边后进行砂带磨削成型的加工工艺,叶片边缘型面轮廓的加工精度要求为0.06mm~0.1mm;表面粗糙度要求为低于Ra0.4μm[2]。
目前国内航发叶片砂带磨削机床的磨削机构主要采用气缸连接导杆,导杆与接触轮连接的方式实现恒压浮动磨削,这种结构的输入激励响应较慢,仅适用于叶片型面的恒压浮动磨削[3]。而叶片边缘曲面的加工余量不均匀,磨削机构需根据曲面的加工余量实时控制接触压力变化,对磨削机构的输入激励响应速度与接触力动态响应特性提出了较高的要求。

图1 航发精锻叶片
2 新型砂带磨削机构结构原理
新型砂带浮动磨削机构由伺服电机产生输入激励,通过弹簧连接丝杆与导杆,实现浮动磨削加工,能较好的适应叶片边缘曲面形状变化,满足叶片边缘结构特点;同时,机构采用伺服电机作为驱动,具有快速的输入激励响应,使用砂带磨削方式,能获得较好的表面粗糙度,满足叶片边缘的加工工艺要求。如图2所示,由图2可知其运动原理:

图2 新型砂带磨削机构原理图
气缸6的气缸杆伸出,使穿过丝杆内孔并连接气缸杆与导杆11的钢丝9处于放松状态,磨削机构通过导杆11与接触轮13的重力向下进刀,接触轮13与工件接触时,导杆11与接触轮13的重力与弹簧10弹力平衡,完成进刀动作。
当需要增加接触力时,伺服电机2通过同步带5快速驱动螺母带轮7反转,螺母带轮7的反转带动丝杆8向下移动,丝杆8的向下移动会使弹簧10产生的弹力减小,这时,导杆11与接触轮13的重力与弹簧弹力的合力就会对工件产生接触力;相反,伺服电机正转则控制接触力的减小。同时,安装在导杆11上的压力传感器12会不间断地向计算机系统反馈接触力信号,计算机系统根据反馈的接触力信号与叶片边缘曲面的加工余量实时调整伺服电机的角位移,从而实现接触力的精确控制。在加工完成时,气缸6收缩气缸杆,钢丝9处于张紧状态,带动导杆11与接触轮13向上运动,实现磨削机构的退刀动作。
3 磨削机构模型建立与仿真分析
3.1磨削机构仿真模型建立
由于ADAMS仿真软件的建模功能较为简单,而砂带磨削机构的模型建立又比较复杂,为了保证模型在仿真时的精度,采用三维软件UG构建砂带浮动磨削机构装配模型。将装配后的三维模型用Parasolid文件导入多体运动与动力学软件ADAMS中,如图3所示。

图3 3D模型导入ADAMS
在ADAMS/View中,砂带与同步皮带的仿真模型建立非常复杂,而其仿真模型的建立对砂带磨削机构接触力分析的影响较小,因此可将砂带的张紧作用对接触力的影响简化为丝杆与导杆之间弹簧的预压紧力;将伺服电机连接同步带轮产生的驱动置于螺母带轮上。由此可得整个系统的约束关系如表1所示。

表1 浮动磨削机构的约束关系
3.2接触力的计算
浮动磨削机构工作时的接触力为接触轮与工件接触而产生的垂直方向的力。在ADAMS/View中有两种计算接触力的方法,一种是冲击函数法(Impact);另外一种是补偿法(Restitution),这两种方法都是对接触约束采用惩罚算法而得到的。根据文献[4-5]知,补偿法(Restitution)较难对参数进行准确设置,因而选择冲击函数法(Impact)计算接触力。根据Impact函数计算两个构件之间的接触力为:

式中K—刚度系数;
x1—两物体要接触的初始距离;
x—两物体碰撞过程中的实际距离;
e—刚性力指数;
C—阻尼系数;
STEP—阶跃函数,可参考ADAMS用户手册
d—阻尼率达到最大所经过的距离。
根据接触的两构件的材料特性[6],确定接触力相关参数如下:
①刚度系数(Stiffness):2855/(N/mm),用于计算接触力法向作用力的材料刚度;
②指数(Force Exponent):2,反映材料非线性程度;
③阻尼系数(Damping):0.57/((N·s)/mm),反映出接触能量的损失;
④渗透系数(Penetration Depth):0.1mm,反映最大阻尼时的侵入深度。
3.3新型砂带磨削机构参数分析
对于新型砂带磨削机构而言,其接触力是由螺母带轮的旋转带动丝杆的上下移动,从而改变弹簧的拉力或压力而产生的。相同输入激励下的磨削机构,在弹簧刚度系数的不同时,会使螺母带轮在相同时间内转过的角位移不同,从而引起接触力最大振动幅值的变化;同时,弹簧阻尼系数与导杆阻尼系数会影响接触力达到稳定状态的时间[7]。由于新型砂带磨削机构的动态响应特性能主要通过接触力稳定时间与接触力最大振动幅值来进行评价。因此,这三个参数的取值对于新型砂带磨削机构的动态响应特性而言十分重要。
在ADAMS中,需将接触力稳定时间与接触力最大振动幅值设定为优化目标函数才能进行优化,而实现上述优化目标函数的设定十分困难。因此,需采用实验设计的方法对弹簧刚度系数、弹簧阻尼系数与导杆阻尼系数三个参数值进行优化设计。根据新型浮动磨削机构的结构设计,设定弹簧阻尼系数取值范围为0.1(N·s)/mm~10(N·s)/mm、弹簧刚度系数取5 N/mm~15 N/mm、导轨阻尼系数取值范围为0.1(N·s)/mm~10(N·s)/mm。选用的伺服电机转速为0 r/min~3000 r/min,航发精锻叶片进排气边缘曲面加工的接触力通常为5N~15N[8],建立实验设计因素水平见表2。

表2 实验因素水平表
对于上述实验因素及水平,若进行全面实验需113次实验,其实验次数过多、实验周期过长。针对这种情况,采用均匀设计法能通过较少的实验次数获得理想的实验结果[9]。根据均匀设计表(114)进行实验安排,如表3所示。

表3 实验安排
4 仿真实验结果及分析
航发精锻叶片进排气边缘在加工过程中对于接触力的控制调整十分频繁,接触力的变化小到0.5N~2N,大到5N~10N。为使砂带磨削机构在接触力的各种变化下都具有良好的动态响应特性,需对不同的输入激励进行实验,砂带磨削系统对弹簧的输入激励为:

式中,φ为螺母带轮角位移(rad);P为螺母丝杆的螺距(mm),根据磨削机构的设计取P=2mm;K为弹簧刚度系数。
现将输入激励分为2N、6N、12N三个水平,对螺母带轮与丝杆的转动约束(Revolute Joint)添加驱动(Motion),分别建立STEP函数:
2N:STEP(time,0,0d,0.01,-360d/K);
6N:STEP(time,0,0d,0.03,-360*3d/K);
12N:STEP(time,0,0d,0.05,-360*6d/K)。
进入仿真界面,设置仿真参数:仿真时间为0.5s,输出结果500次。对不同的输入激励分别按照表3进行仿真实验。每组参数值的仿真实验完成后,进入PostProcessor界面中,测量出接触力曲线,将相同输入激励下的各组仿真实验的接触力曲线输出到同一图表中进行对比,如图5~图7所示。

图5 输入激励为2N的接触力曲线
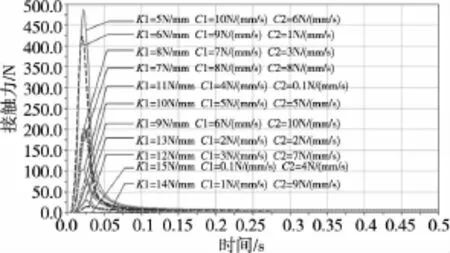
图6 输入激励为6N的接触力曲线
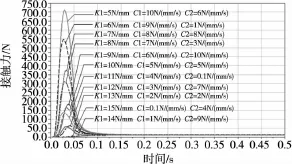
图7 输入激励为12N的接触力曲线
在PostProcessor界面中,通过工具栏的曲线跟踪(Plot tracking)功能,可以对每一组仿真实验的接触力曲线的相关特征数据进行提取。使用此功能可获得各组仿真实验的接触压力最大振动幅值、稳定时接触力值以及稳态偏差为±0.05N时的接触力稳定时间。
为方便对比不同实验因素水平以及不同输入激励下的接触力稳定时间、接触力最大振动幅值与稳定时接触力值,对上述获得的各值输入图8~图10所示图表中进行对比。
根据图8~图10的实验结果对比分析可知,当弹簧刚度系数为 13N/mm、弹簧阻尼系数为 2(N·s)/mm、导轨阻尼系数为2(N·s)/mm(实验序号9)时,浮动磨削机构在各接触力激励水平下的接触力稳定时间均较短,分别为0.016s、0.094s、0.09s;且接触力最大振动幅值均较小,分别为1.71N、29.19N、57.94N;稳定时接触力分别为1.12N、4.77N、10.48N。
根据优化后的弹簧刚度系数、弹簧阻尼系数与导杆阻尼系数,对螺母带轮添加新的驱动,建立STEP驱动函数,具体函数值为:STEP(time,0,0d,0.03,-360* 3d/13)+STEP(time,0.2,0d,0.23,-360*3d/13)+ STEP(time,0.4,0d,0.45,-360*6d/13)。进入仿真界面,设置仿真参数:仿真时间为0.6s,输出结果500次。进行仿真,进入PostProcessor界面中,测出磨削机构运动相关曲线,如图11所示。

图8 接触力稳定时间对比

图9 接触力最大振动幅值对比
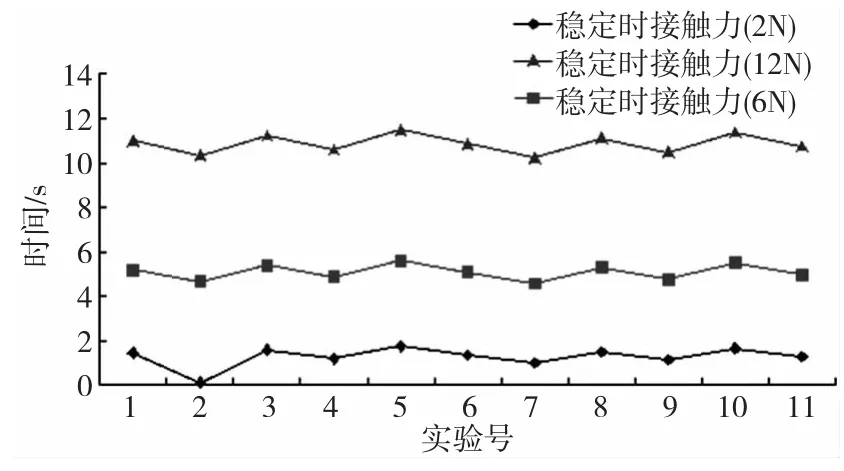
图10 稳定时接触力对比

图11 接触力仿真曲线
由图11知,接触力的变化趋势与螺母带轮角位移、弹簧变形量相一致,与实际相符。对优化后的新型砂带磨削机构的接触力进行多次调整,其输出的接触力均能在0.1s内达到稳定状态,接触力控制精度为±0.05N,且接触力最大振动幅值均较小。优化后的新型砂带磨削机构具有较好的接触力动态响应特性及较高的接触力控制精度,满足航发精锻叶片边缘磨削加工的要求。
5 结论
本磨削机构采用伺服电机、螺母丝杆与弹簧的结构,实现航发精锻叶片边缘的浮动磨削加工,具有快速的输入激励响应。通过ADAMS仿真分析与均匀实验设计方法,对该机构的弹簧刚度系数、弹簧阻尼系数与导杆阻尼系数进行优化设计,优化后的磨削机构的接触力能在0.1s内达到稳定状态,接触[参考文献]
力控制精度达到±0.05N,且接触力最大振动幅值较小,具有良好的动态响应特性以及较高的接触力控制精度,能够满足航发精锻叶片边缘磨削加工的要求。
[1]张岳.航发叶片七轴联动数控砂带磨削加工方法及自动编程关键技术研究[D].重庆:重庆大学,2012.
[2]蔺小军,汪文虎,单晨伟.航空发动机叶片加工新工艺研究[J].航空精密制造技术,2009(5):46-48.
[3]黄智.叶片型面数控砂带磨削技术基础及应用研究[D].重庆:重庆大学,2010.
[4]蒲明辉,吴江.基于ADAMS的链传动多体动力学模型研究[J].机械设计与研究,2008(2):57-59.
[5]刘凡,芮延年,吉绍山.基于Pro/E和ADAMS的步进机构的仿真[J].机械传动,2013(3):40-44.
[6]孔祥安.固体接触力学[M].北京:中国铁道出版社,1999.
[7]田启华,汤伟毕,杜义贤.基于虚拟样机的数控插齿机减速箱动力学分析[J].组合机床与自动化加工技术,2013(6):44-46.
[8]吴海龙.航空发动机精锻叶片数控砂带磨削工艺基础研究[D].重庆:重庆大学,2012.
[9]刘文卿.实验设计第一版[M].北京:清华大学出版社,2005.
[10]田会方,林喜镇,赵恒.基于Pro/E和ADAMS齿轮啮合的动力学仿真[J].机械传动,2006(6):66-69,98.
[11]刘虹,牛玉荣,倪冬.基于UG和ADAMS的TI蜗杆传动建模与动力学仿真[J].组合机床与自动化加工技术,2013(4):118-121.
(编辑 赵蓉)
Optimization Design of Aeroengine Precise Forging Blade Edge Belt Grinding Mechanism Based on ADAMS
ZHAN Fei,ZHANG Ming-de,ZHANG Wei-qing,XU Hao-chi
(School of Mechanical Engineering,Chongqing University of Technology,Chongqing 400054,China)
To achieve the floating and grinding of the blade edge of Aeroengine precision forging,a new belt grinding mechanism which mainly consists of servomotor,screw-nut pair and the spring structure is designed.Based on software platform of Adams,the contact pressure curve through simulating of the new belt grinding mechanism is obtained.According to the contact pressure curve,using uniform experimental design,optimizing the coefficient of spring stiffness,spring damping,guide rod damping,reduced the stable time of contacting pressure to 0.1 seconds after optimized new belt grinding mechanism,and the maximum vibration amplitude of the contact pressure is small than others,it proved that the design of the new belt grinding mechanism has good dynamic response characteristics of contact pressure.
blade edge;belt grinding;ADAMS;motion simulation
TH122;TG65
A
1001-2265(2015)02-0017-04 DOI:10.13462/j.cnki.mmtamt.2015.02.005
2014-11-04;
2014-12-09
“高档数控数控机床与基础制造装备“国家科技重大专项(2014ZX04001031);重庆市应用技术研究项目(cstc2012gg-yyjs70006)
詹飞(1987—),男,四川广安人,重庆理工大学硕士研究生,研究方向为复杂曲面零部件智能化制造与检测,(E-mail)272028996@qq. com;通讯作者:张明德(1975—),男,四川苍溪人,重庆理工大学副教授,研究领域为复杂曲面零件智能化制造及检测,(E-mail)zmd @cqut.edu.cn。

