一种新型球形机器人的结构设计*

林星陵，陈建毅

（厦门城市职业学院机械与自动化工程系，福建厦门 361008）

一种新型球形机器人的结构设计*

林星陵，陈建毅

（厦门城市职业学院机械与自动化工程系，福建厦门 361008）

针对目前球形机器人存在的结构复杂，控制困难等问题。在基于重心偏摆与力矩复合驱动的原理上，文章设计了一款控制配重块摆动的新型遥控球形机器人，重点分析其运动原理，建立系统的数学模型，并制作了一台样机。实验测试表明：该球形机器人的结构简单，可实现沿任意曲率的曲线运动以及任意转向的控制，且定位性能和复位性能好。

球形机器人；全向运动；减速电机

0 引言

球形机器人是近年来出现的一种新型机器人系统，是一种将所有零部件都内置到球壳内的封闭式系统。目前，球形机器人研究重点主要在驱动装置和控制算法两个方面。在驱动装置方面有单轮驱动、小车驱动、万向轮驱动、电机定子反转驱动和配重块驱动等，这些球形机器人采用了不同的驱动方式实现了球体的滚动［1-5］。但这些设计方案中均未在球壳内部设计一个相对稳定的工作平台，此外，还存在控制麻烦，能耗较大，不适合在路况较差的路面行走等缺点。

针对球形机器人结构方面问题进行改进，本文提出一种控制配重块摆动的新型球形机器人结构，所设计的球形机器人由于重心偏下可具有不倒翁的特点，在任何情况下都可以自动恢复到平衡状态，即使是与障碍物发生碰撞也会再经过短暂的不规则运动后恢复，所以此类球形机器人适合于在不方便人为直接干预的环境中运行，如管道、危险环境等［6-7］。

1 球形机器人的结构设计与运动分析

1.1 结构设计

本文设计了一款体积适中的遥控球形机器人，通过遥控器的控制，使球形机器人能按照要求的轨迹和速度到达指定位置，其三维结构如图1所示。

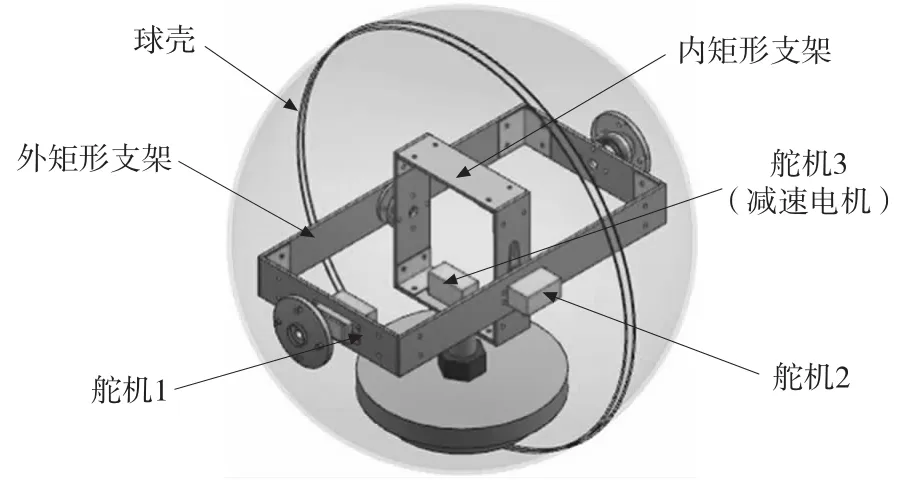
图1 球形机器人三维结构图

在球形机器人内部装有内外两个矩形支架，外矩形支架通过轴承与球壳实现滚动连接，通过控制外矩形支架带动配重块的摆动实现球体的直线运动，在外矩形支架上还可安装摄像头、驱动电源、控制电路等。内矩形支架与外矩形支架通过轴承、摇臂等连接，通过控制内矩形支架带动配重块的摆动实现球体的转弯。内矩形支架下面安装一配重块。

1.2 运动分析

在球形机器人系统中，当机器人处于稳定状态时，整个系统的重心与其支撑点在同一竖直线上，且重心位于最低点，通过改变球体重心的位置，使重力线相对于球体偏离其支撑点，从而得到一偏心力矩，进而实现球体的滚动［8-9］。这是球形机器人最基本的运动原理。

当整个系统的中心与球体的重心在同一竖直线上时，球形机器人处于静止状态。要使机器人运动起来，需启动系统的三个舵机，通过遥控器控制舵机1和舵机2在球壳内转动，以此来改变配重块的位置。此时，系统的重力和地面对球体的支撑力形成一个力偶，该力偶驱动球壳在平面上滚动［10］。在图1中，角度舵机1输出轴通过法兰盘与球壳相连接，当其转动时，会带动外矩形框架绕其轴线旋转一角度，这样系统就出现了重心偏移力矩驱动球形机器人实现直线滚动。球形机器人在直线运动过程中，通过与内矩形支架相连接的角度舵机2驱动配重块沿中心轴线向一侧摆动并与轴线形成一定夹角，重心的改变使得球形机器人与地面的接触点移动，从而实现球形机器人的转弯运动。转弯半径大小取决于配重与中心轴线的夹角，夹角越小，转弯半径就越大。舵机3（减速电机）与内矩形支架连接，通过控制舵机3自旋转运动，能实现球形机器人的任意转向。

2 球形机器人的运动学分析

球形机器人的舵机控制系统主要实现舵机1和舵机2的控制，要使三个舵机达到良好的控制性能，需建立正确的球形机器人数学模型。简化后的球形机器人重心偏离示意图如图2所示，运动简图如图3所示［11-12］。球壳及内外矩形框的重心在O1，由于球壳及内外矩形框为对称结构，其在运动过程中重心不会变化，单独内外矩形框的摆动并无法改变球体重心的位置。配重块的重心在O2，通过调整配重块的位置可以改变整个球形机器人重心位置，从而达到控制球形机器人滚动。

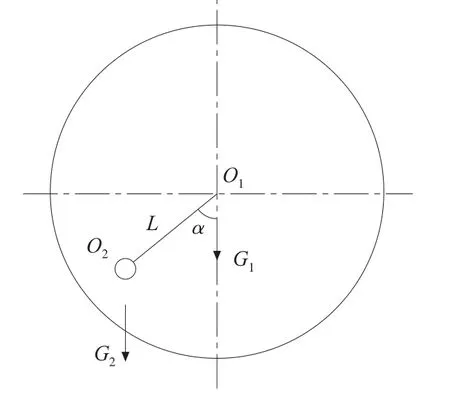
图2 球形机器人重心偏离示意图

如图3，xyz为世界坐标系，则xoy为球形机器人滚动的平面，XYZ为运动坐标系，球形机器人在xoy面内沿路径p（t）做曲线运动，m点为球壳与xoy平面的作用点［11-12］。α为O1O2与O1Z轴的夹角，即球体运动过程中配重块摆动的角度，α越大，则球体滚动速度越快，α的极限范围为-90°到90°。β为O1O2在XY平面内的投影与O1X轴的夹角，β的大小控制着球体转弯半径的大小，β越小，转弯半径越大，当β=0°时，球体做直线运动。由此，可以得到配重块重心O2点相对于XYZ坐标系的坐标值为（L sinαcosβ，L sinαsinβ，L cosα），此时，配重块重力和地面对球体的支持力形成一个力偶，驱动球形机器人在平面上滚动。

图3 球形机器人运动简图

根据图3的运动简图，可以定义变量；

（1）理想状态下，球壳与xoy面的作用点m在坐标系xyz的坐标为（x，y，0）。

（2）球体相对于世界坐标系的方位，由θ1，θ2，θ3定义，其中θ1，θ2，θ3分别为运动坐标系XYZ相对于世界坐标系xyz的欧拉转角。

（3）定义i，j，k为运动坐标系O1X轴，O1Y轴，O1Z轴的单位矢量。

设VG为球心O1的直线速度，ω为球体的角速度，r为球心O1到m点的矢径O1m，可以得到球体的角速度方程如下［12-13］；

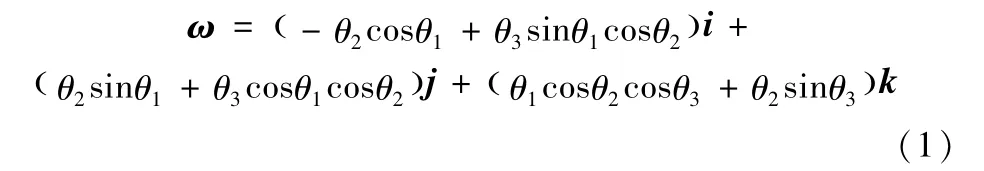
在理想状态下，球只做纯滚动，所以球与xoy平面的作用点m相对于地面的运动速度Vm=0。得到

又有r=-r k，其中r为球壳半径。将式（1）代入式（2）可得；

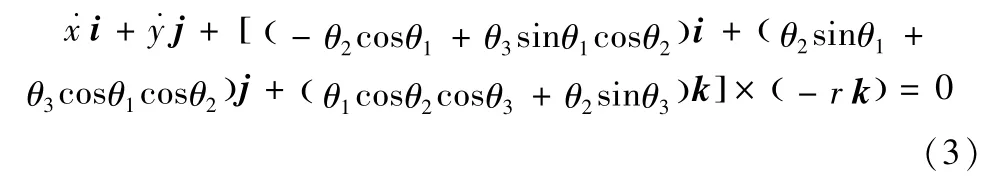
可以得到

将两个分运动合成，可得机器人的瞬时运动速度为；

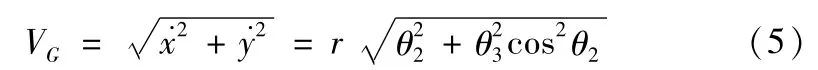
由此可见，该机器人的运动速度是由θ2和θ3来决定，因此可以通过调整舵机1和舵机2来分别控制θ2和θ3，即可达到控制球形机器人速度的要求。

通过对速度进行积分运算，可以得到球形机器人在世界坐标系中的位置关系；

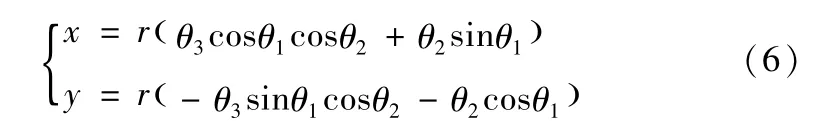
由图3可看出，球心的位置只是在z方向和m点有所区别。由（6）可见，球形机器人球心的位置是由θ1，θ2和θ3来决定，因此，控制了θ1，θ2和θ3就控制了球形机器人的运动位置。

3 样机验证

根据本文所设计的球形机器人结构进行了样机的制作，如图4所示。球体直径400mm，球壳材料为亚克力，以保证与外部的通信，内外矩形框及配重块均采用铝，利用太阳能电池板供电。

图4 球形机器人样机

经过样机实验，采用遥控器控制方式，验证了该设计方案的正确性。通过控制舵机1，成功实现了球体的直线运动。通过控制舵机1和2，成功实现了球体的转弯运动。通过控制舵机3，成功实现球体原地360°旋转。实验测试表明该球形机器人的结构是合理的，可以实现任意方向的运动和转向的控制。

4 结论

本文设计的球形机器人控制配重块摆动的内外矩形支架结构相互垂直，运动过程完全独立，均可进行独立的运动控制，相比之前的各球形机器人而言，可真正实现沿任意方向的直线运动或曲线运动。内矩形支架上的减速电机可实现球形机器人任意方向的转向。

在该球形机器人的结构上使用了两垂直相交且中心重合的框架结构，构思独特，具有创新性。从设计角度讲，该球形机器人为单层球体结构，结构简单，球体重心易于控制，并可安装各种探测设备，有较强的适应环境的能力等。为球形机器人的进一步实际应用和研究提供了一个实用有效的平台。

［1］李团结，苏理，张琰.直线电机驱动的全向滚动球形机器人的设计与分析［J］.机械设计与研究，2006，22（4）；46-52.

［2］江洁.内外驱动兼备的球形机器人设计及性能分析［D］.西安；西安电子科技大学，2010.

［3］赵勃，孙立宁，李满天.球形机器人研究综述［J］.机械与电子，2010（9）；65-70.

［4］张义刚.一种球形机器人的运动规划和控制研究［D］.西安；西安电子科技大学，2006.

［5］岳明.双驱动球形机器人及其运动控制的研究［D］.哈尔滨；哈尔滨工业大学，2008.

［6］战强，贾川，马晓辉，等.一种球形移动机器人的运动性能分析［J］.北京航空航天大学学报，2005，31（7）；46-49.

［7］刘大亮.一种球形移动机器人的运动分析与控制技术的研究［D］.北京；北京邮电大学，2009.

［8］聂志萍，董万福.一种全向滚动球形机器人运动结构的创新设计［J］.成都大学学报（自然科学版），2009，28（3）；63-65.

［9］付清岭.全方位球形机器人的研究［D］.北京；北京邮电大学，2003.

［10］刘彦翀.应用于球形机器人内部的双轴稳定平台研究［D］.北京；北京邮电大学，2010.

［11］孙汉旭，肖爱平，贾庆轩，等.二驱动球形机器人的全方位运动特性分析［J］.北京航空航天大学学报，2005，31（7）；37-40.

［12］白杰，党建军，张谋，等.一种新型球形机器人机构设计及运动仿真［J］.机械与电子，2008（11）；73-75.

［13］李团结，朱超.一种具有稳定平台可全向滚动的球形机器人设计与分析［J］.西安电子科技大学学报（自然科学版），2006，33（1）；53-56.

（编辑 李秀敏）

Structural Design of a New Kind of Spherical Robot

LIN Xing-ling，CHEN Jian-yi
（Department of Mechanical and Automatic Engineering，Xiamen City University，Xiamen Fujian 361008，China）

；Conventional spherical robots have the problems of complex structure and difficult control.To overcome these shortcomings，a new kind of remote control spherical robot by controlling the counterweight swing was designed，which driven by composite of gravity deviation and inertial moment.Its motion principle was analyzed and the mathematical model of the system was created.Furthermore，a prototype of this kind spherical robot was manufactured.The experimental results show that the structure of the spherical robot is simple.It can move along arbitrary curvature curve and arbitrary steering.Furthermore，it can achieve better localization performance and reset property.

；spherical robot；omni directional movement；gear motor

TH122；TG65

A

1001-2265（2015）05-0104-03 DOI：10.13462/j.cnki.mmtamt.2015.05.029

2014-08-25；

2014-12-15

2014年福建省高校杰出青年科研人才培育计划资助（JA14424）；厦门城市职业学院院级课题（KYQK2014-17）；厦门城市职业学院机电技术应用研究所科研平台

林星陵（1981—），男，福建南安人，厦门城市职业学院讲师，硕士，研究方向为机械设计，（E-mail）linxl519@qq.com。