单元模块备课 整体把握教材

黄丽红

基于当前教材的编排模式，编者试图通过一个单元模块实现某一专题的知识教学和技能掌握，让学生通过学习形成相对完整的知识体系。笔者将一个单元作为一个模块，从整体上考虑教学思路，有目的、有计划地备好具有关联意义的一类课，以明晰知识间的内在联系，力图有效构建知识网络，提高学生的思维品质和结构迁移能力。

一、通读教材，制订单元教学目标

数学中的学习单元并不是以某个主题为纽带将各部分内容简单地串联和相加以产生知识累加效应，而是有机地整合成一个模块。这就要求教师在备课时不能孤立地进行某一课时的设计，而应通读单元教材，大致了解整个单元的教学内容，系统分析解读例题所蕴含的知识技能、思想方法，以整体的视角统观教材，制订单元教学目标，把握单元教学要求。

以人教版一下第二单元“20以内的退位减法”单元教学模块通读为例。

1.十几减9（例1）。

分析解读：情境图→找数学信息、问题→点子图→算式计算，通过摆一摆、画一画，把具体的操作过程与抽象的计算方法相对应，让学生理解算理，掌握“破十法”“想加算减”等方法，体现算法多样，为学生脱离实物计算做好铺垫，同时渗透符号思想、抽象思想和集合思想。

2.十几减8（例2）。

分析解读：运用知识的迁移，借助例1的方法学习。学生根据情境图列出算式后，还应让学生通过摆一摆、画一画，展示“破十法”和“想加算减”等算法，在讨论和自我反思的基础上，确定适合自己的算法。

3.十几减7，十几减6（例3）

分析解读：根据金鱼池中红金鱼和黑金鱼的数量分别提出问题，引出13-7和13-6两道算式。然后让学生自己进行计算，学生用哪种计算方法都可以，把“教方法”转变为学生自觉构建方法。

4.十几减5、4、3、2（例4）

分析解读：教材脱离了直观的情境图，直接出示算式，启发学生迁移类推，用自己喜欢的方法计算，鼓励学生自主讨论，交流算法，培养学生抽象思维能力和知识迁移能力。

5.解决问题（例5，例6）

分析解读：①把握三点：一是有多余条件，二是用摆小棒（或画图）帮助理解数量关系，三是学习口答结果并填写答话中的数。②教学解决“求一个数比另一个数多几”的问题，重在借助摆圆片（或画图）帮助学生理解数量关系，使学生明确“谁多？谁少？谁比谁多？”再列出算式。“求一个数比另一个数少几”的问题则安排在“做一做”中。

6.整理和复习。

分析解读：①将20以内的退位减法算式进行整理，引导学生填写算式并发现算式排列的规律，梳理算法，回顾反思，加深对20以内退位减法的理解和记忆。②情境图给出了一个数学信息，另一个数学信息需要学生根据问题摒弃多余条件去寻找，以便学生进一步掌握解决问题的方法。

二、精读教材，凸显教学指导重点

单元模块内的每一部分内容，都从不同的侧面充实着单元主题。因此，在备课研讨时，教师要从知识的整体结构入手来研究每一个局部知识、技能的地位和作用。教师围绕单元教学目标层层深入精读教材，研读例题，在方法、思路看似相同的教学内容中剖析出每部分内容承载任务的不同，从而合理设计教学进程，突出教学指导重点。

例如人教版五上“多边形的面积”单元，整个单元都要突出转化思想，但单元模块内各个部分内容转化思想的运用是有侧重的。平行四边形面积计算公式的推导重在“扶”，引导学生通过剪拼实现平行四边形到长方形的转化，把新知转化为旧知解决问题。三角形的面积公式推导，教师要重点引导学生经历“破”与“立”的过程：学生会自觉迁移平行四边形面积推导的方法，试图通过用剪拼一个三角形的方法探求它的面积公式，学生任意剪拼后发现此法不具普遍性（要沿中位线剪才行），从而感受到看起来行，实际上不行的“破”的过程。在此基础上教师再着重指导学生用两个一样的三角形拼成一个学过的图形，从图形之间的关系推导出三角形面积计算方法。到梯形的面积计算时，则应突出“放”，要求学生综合运用学过的方法自己推导出面积计算公式。以上三种图形面积计算公式推导的思路一样——都是转化为已学的图形进行推导，但体验不同——如何转化，转化为什么图形，由此引发的教学指导重点也就不同，学生所经历的思维活动和学习收获也不尽相同。

三、横向联系，沟通知识内在联系

数学中各部分知识联系密切，新知识往往是旧知识的深化和发展，教师应引导学生把握知识的内在联系，经历知识从薄到厚、又从厚到薄的过程，融合表面看似毫不相关的各类知识，提高知识整合能力。

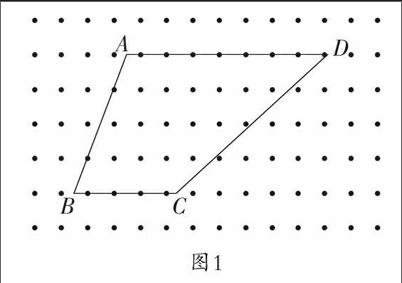
例如人教版四上第五单元“平行四边形和梯形”的备课。教师应立足整体，引导学生横向比较，沟通平面图形间的内在联系。教师可利用图1引发学生思考、想象：

①随着C点在直线上左右移动，会变成哪些图形呢？

②如果在直线上移动两个点，能得到什么图形？

③如果随意移动C点，又会变成什么图形？

让学生由静态图形联想到动态结果，通过点的动态变化想象图形的变化，再用课件进行验证，动静结合，以“动”促“思”，不仅深刻认识了图形的特征，沟通了平面图形之间的联系，又发展了学生的空间观念。

四、纵向联系，实现知识结构迁移

教师在进行单元备课时，应把不同年级知识纵向关联起来进行整体设计，通过连续递进的教学设计来培养学生的类比迁移能力。

例如，人教版三下第六单元“面积”的备课时，就要把它和低年级的长度概念、长度单位，高年级的体积概念、体积单位关联起来，因为这些知识虽然编排在不同的年级，却是一类纵向的有内在联系的知识。备课时要思考琢磨“种子课”（长度单位）应渗透什么数学思想和学习方法，该积累哪些学习活动经验。“生长课”的知识连接点和生长点在哪里，和后续的学习有什么关系，该如何为学生提供主动迁移的学习机会，把过去、现在和未来的学习关联起来备好一类课，不仅能让学生理清知识的来龙去脉，主动实现知识之间的结构迁移，还能有效提高教师的系统思维和整体策划能力。

（作者单位：福建省龙岩市普通教育教学研究室 责任编辑：王彬）endprint