服用织物拉伸性能的各向异性分析

潘 月，岑 洁，游晓悦，杨允出，b

（浙江理工大学，a.服装学院；b.浙江省服装工程技术研究中心，杭州310018）

服用织物拉伸性能的各向异性分析

潘 月a，岑 洁a，游晓悦a，杨允出a，b

（浙江理工大学，a.服装学院；b.浙江省服装工程技术研究中心，杭州310018）

为了揭示低应力作用下不同拉伸方向对织物拉伸性能的影响，采用Instron3344测试仪对4种机织物和4种纬编针织物进行测试及统计分析。主要研究内容包括：建立拉伸应变和弹性模量与拉伸角度之间的变化曲线，并阐述它们的变化规律；通过SPSS的非线性回归分析建立拉伸应变和弹性模量与拉伸角度之间函数关系的拟合方程。结果显示：机织物与纬编针织物在拉伸性能的各向异性方面具有不同的曲线特征，所建的三角函数拟合方程均具有较高的拟合优度。

织物；拉伸性能；各向异性；非线性回归

0　引 言

服用织物力学性能的各向异性对织物外观、缝制加工性能以及服装款式设计等都有重要的影响。为了揭示织物在不同方向的织物拉伸、弯曲等基本力学性能，许多学者进行了相关研究。张芝兰等［1］基于正交各向异性材料的力学原理，分析推导了任意方向上织物拉伸弹性模量与经、纬向拉伸弹性模量、剪切模量、柏松比以及拉伸角度之间的理论公式。李焰等［2］调查了平纹机织物在不同方向的断裂强力、断裂伸长率、定伸长弹性和折皱弹性等指标。洪维亚等［3］、谭磊等［4］对针织物在不同方向上的拉伸性能进行测试，并分析了影响断裂强力、断裂伸长和拉伸模量的因素，以及各指标与拉伸方向角之间的三角函数关系。徐军等［5］分析了在不同方向的织物弯曲长度、抗弯刚度、悬垂性能的影响。倪红等［6］基于BP神经网络对织物斜向弯曲刚度进行预测研究。但这些研究在拉伸性能方面重点分析的是断裂条件下的织物各向异性行为。一些研究还分析了不同方向对缝制、粘合加工后织物外观和性能的影响。如：朱柳静等［7］研究薄型丝织物在不同方向上的力学性能变化，并分析斜向织物延伸性、成形性和弯曲刚度对缝缩率和主观缝皱等级的相关性。Kristina等［8-9］调查了不同粘衬方向对粘合后织物的拉伸应变、拉伸回弹性、拉伸功和拉伸线性度等指标的影响。另外，随着三维服装CAD和动画领域对模拟织物真实性的要求不断提高，织物各向异性也已成为织物力学建模所考虑的重要因素之一［10］。

本文将在前人研究基础上，重点分析在低应力作用下织物拉伸性能的各向异性行为，为服装设计、生产及织物力学建模提供参考。

1　实验及方法

选取8种常用织物，其中机织物4种，针织物4种，其织物规格见表1。实验中织物拉伸方向共选取19个。（取纬向为0°）在0～180°区间，每隔10°取一个拉伸方向（见图1），按照图2的版样裁剪织物试样，并按20 cm×5 cm规格进行裁剪。测试实验前，织物放置在标准大气状态下静置24 h，然后采用Instron3344仪器进行拉伸性能测试。测试中仪器夹具的拉伸速度为100 mm/min，试样实际夹持长度为10 cm，并保持夹具边缘与试样上边缘平行，保证试样自然垂直。

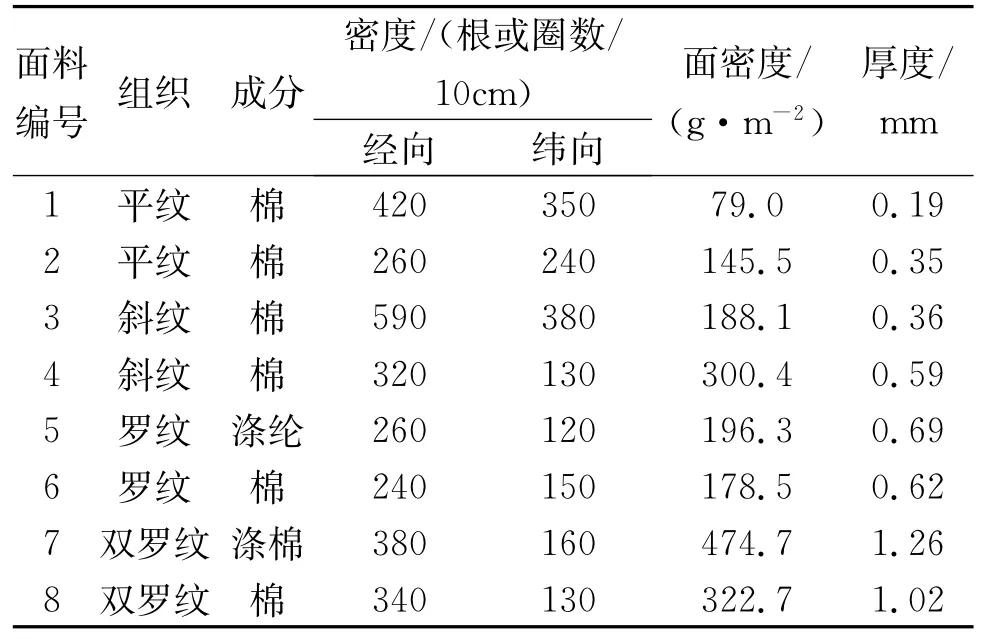
表1　织物规格参数

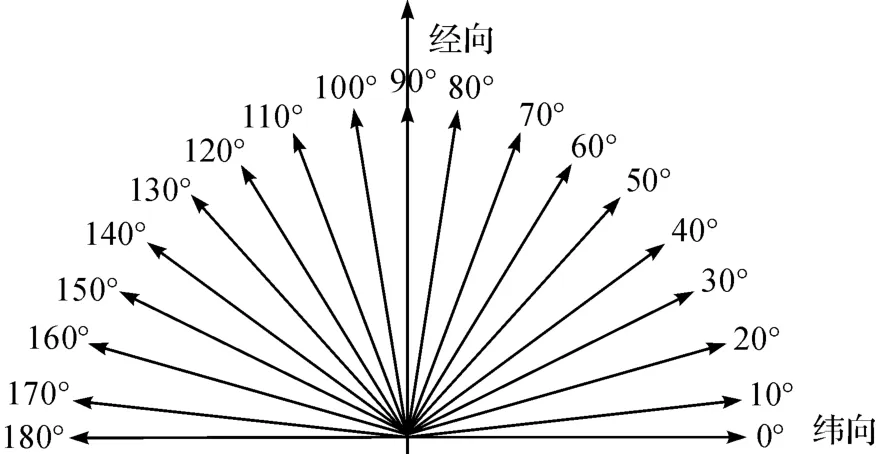
图1　织物拉伸方向的定义

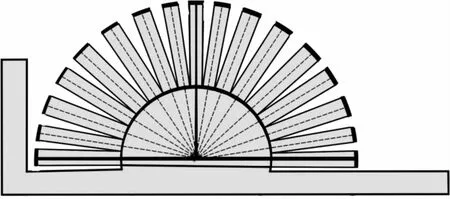
图2　试样裁剪版样

2　测试结果及分析

本文根据实验测得织物的拉伸特性及载荷范围（保证织物拉伸过程中无破损），并参考KES低应力下拉伸测试的载荷条件（500cN/cm），从而对机织物取25 N的载荷条件，针织物由于弹性较大而取10 N载荷条件，分别对它们的拉伸应变和弹性模量与拉伸角度之间的曲线关系进行分析。主要分析内容有：a）建立拉伸应变、弹性模量与拉伸角度之间的曲线，并描述其变化关系；b）通过SPSS非线性回归分析建立拉伸应变、弹性模量与拉伸角度之间的函数关系式。拉伸应变ε和弹性模量E的定义参见式（1）、式（2）；c）分析拉伸拟合函数中所包含的变化规律。

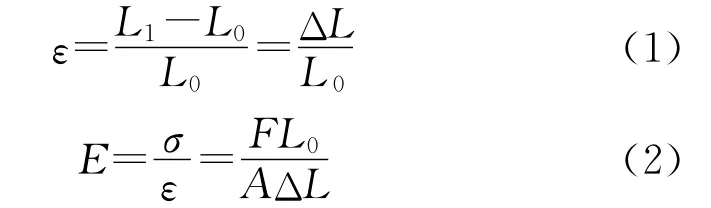
式中：L0为试样原始长度；L1为试样拉伸后的长度；ΔL为试样拉伸位移；A为试样横截面积；E为拉伸载荷；σ为拉伸应力。

2.1织物拉伸应变与拉伸角度的关系

2.1.1机织物拉伸应变与拉伸角度的关系

图3（a）给出了4种机织面料的拉伸应变与拉伸角度之间关系的实验数据和拟合曲线。由图3（a）可知，4种机织物的拉伸应变与拉伸角度的关系曲线均接近三角函数的波形规律，且0～90°区间和90°～180°区间的拉伸曲线形状呈近似对称关系。一般沿经向（90°）和纬向（0°）拉伸时，应变处于曲线低谷，斜向拉伸时，应变增大，在45°和135°附近出现拉伸应变的最高值，达到曲线波峰。不同织物拉伸性能有所差异，不同拉伸曲线的波幅有一定的变化。另外由于实验误差等因素的影响，0～90°区间和90°～180°区间的曲线形状也不完全对称。其中面料1、2和4对应的平纹布1、平纹布2和斜纹布2（面料4）的拉伸性能较接近，且纬向拉伸应变均大于经向；而面料3的拉伸曲线的波幅相对较小，且经向与纬向的拉伸应变值接近。

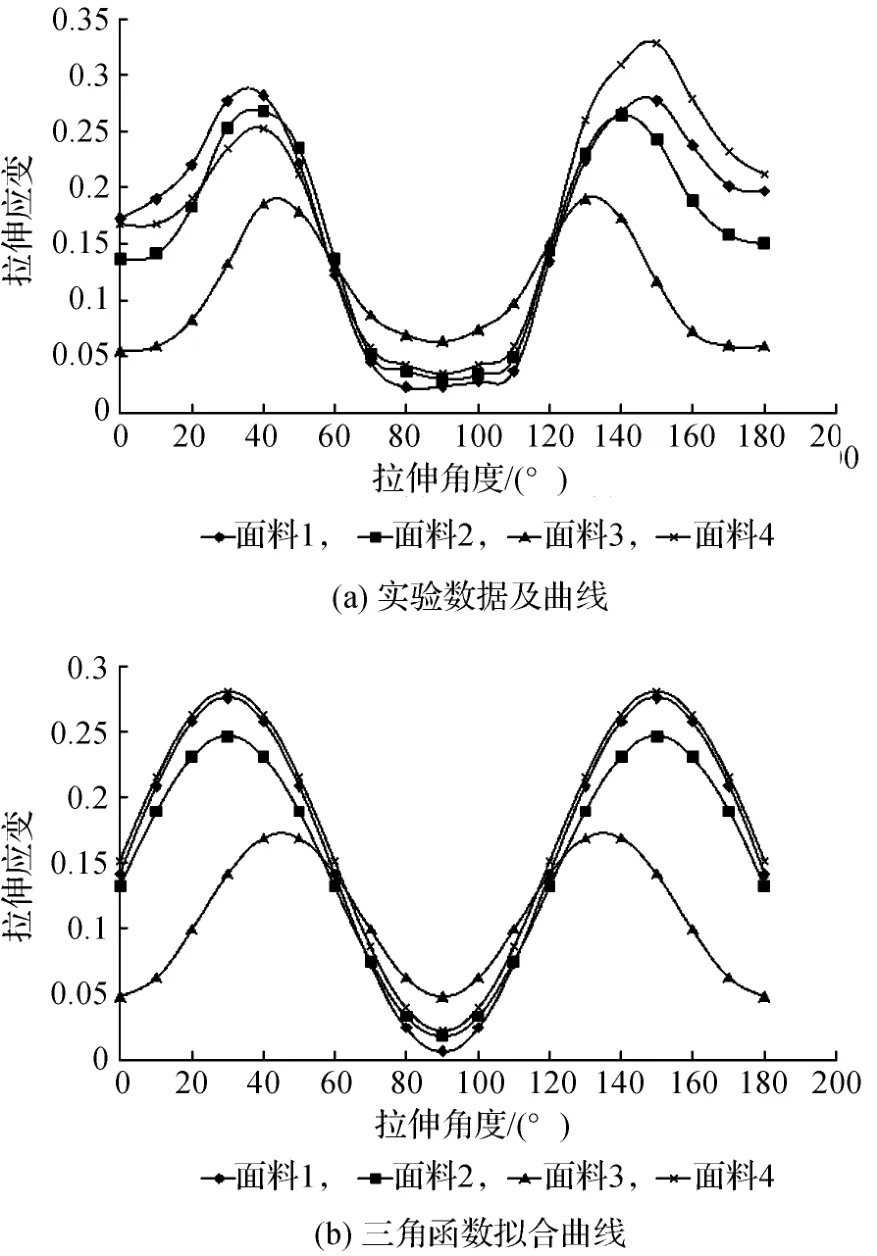
图3　机织物拉伸应变—拉伸角度的变化关系

根据曲线波形特征，进一步通过SPSS非线性回归分析，可得到不同机织物拉伸应变-拉伸角度曲线的回归方程（见表2）和三角函数拟合曲线（见图3（b））。

表2　机织物拉伸应变与拉伸角度非线性回归方程

2.1.2针织物拉伸应变与拉伸角度的关系

图4给出了纬编针织物试样的拉伸应变与拉伸角度之间关系的实验数据和拟合曲线。由图4可知，4种纬编针织物的拉伸曲线均呈中间下凹的形状。由于4种针织物在材料、结构等方面的差异，曲线下凹幅度呈现出较大差异，其中面料7为结构紧致的2+2涤棉罗纹组织，不同角度的拉伸应变值变化较大；面料5和6线圈结构较为疏松，拉伸应变曲线较为接近且各角度的差异不大；面料8的拉伸应变随角度的变化最为平稳。与机织物相比，纬编针织物的拉伸曲线在形状上存在较大差异，在0～90°区间和90～180°区间的曲线分别为单一的下降趋势和单一的上升趋势。四种针织物均在0°（纬向）时拉伸应变最大，在90°（经向）时拉伸应变最小，而机织物一般为斜向拉伸应变最大。

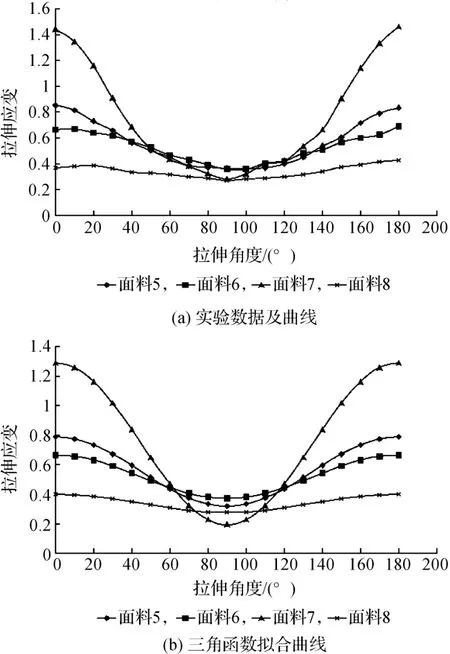
图4　针织物拉伸应变—拉伸角度的变化关系

根据实验数据得到曲线的波形特征，进一步通过SPSS非线性回归分析，就能得到不同针织物的拉伸应变-拉伸角度曲线的回归方程（见表3）和三角函数拟合曲线（见图4（b））。

表3　针织物拉伸应变与拉伸角度的非线性回归方程

2.2织物弹性模量与拉伸角度的关系

2.2.1机织物弹性模量与角度的关系

图5给出了4种机织物的弹性模量与拉伸角度关系的实验数据和拟合曲线。由于指标定义不同，织物的拉伸弹性模量曲线与拉伸应变曲线在形状上有较大差异。由图5（a）可知：面料3对应的斜纹布1的弹性模量曲线，在0～180°区间呈现较有规律的波形曲线特征；面料1、2和4对应的平纹布1、平纹布2和斜纹布2（面料4）在60～120°区间呈现单波峰的曲线形状，而在其它区间弹性模量值的变化较为平缓。根据曲线波形特征，进一步通过SPSS非线性回归分析，可得到织物弹性模量—拉伸角度曲线的回归方程（见表4）和三角函数拟合曲线（见图5（b））。

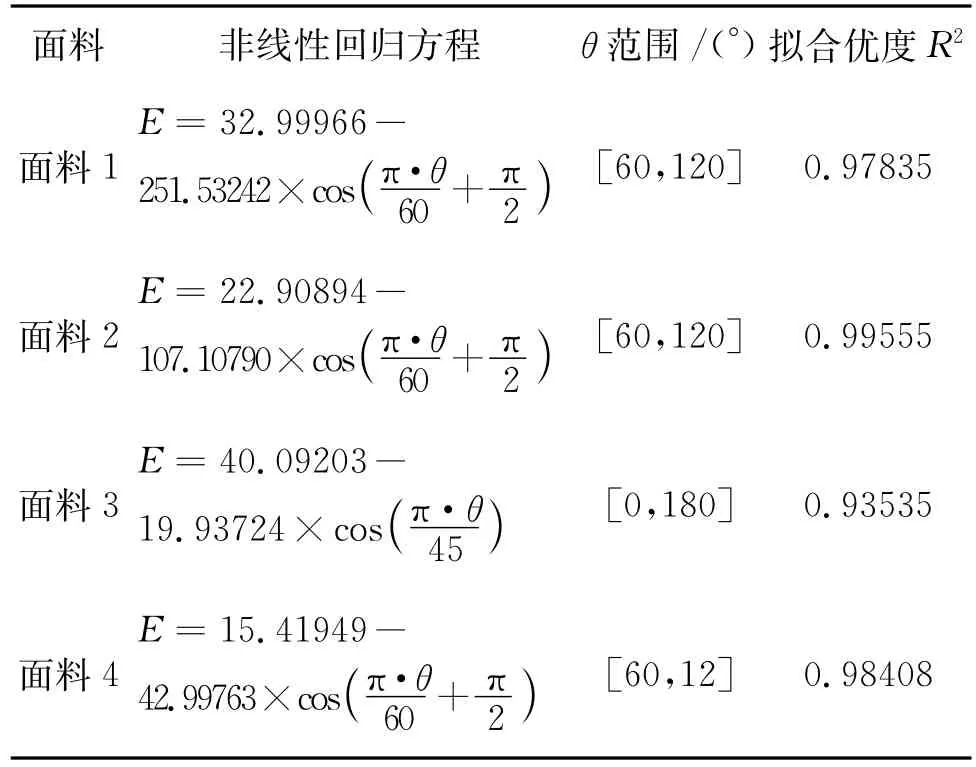
表4　机织物弹性模量与拉伸角度的非线性回归方程

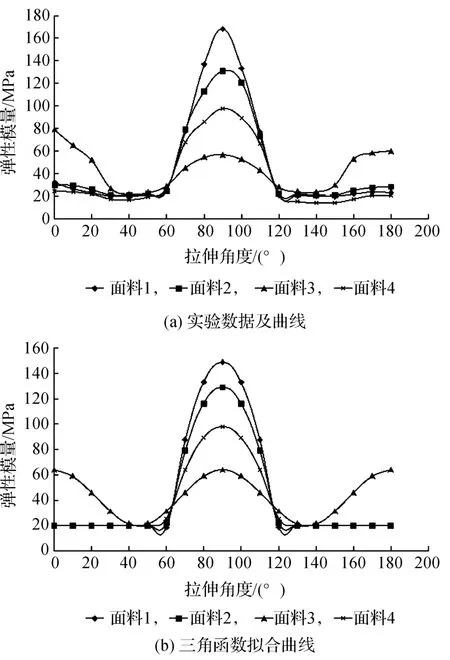
图5　机织物弹性模量—拉伸角度的变化关系

2.2.2针织物弹性模量与拉伸角度的关系

表5和图6给出了4种纬编针织物的弹性模量与拉伸角度关系的实验数据及预测拟合曲线。与机织物不同，4种纬编针织物的曲线形状在0～180°整个区间呈中间凸起的波峰形状。由于面料拉伸性能和厚度的差异，它们各自对应的弹性模量随角度的分布曲线也有一定差异。可以看到它们的曲线波形图形态上都较为接近，都相对于90°呈对称分布，这与其编织结构上的对称性有密不可分的关系。4种针织物的弹性膜量的峰值和谷值分别出现在经向和纬向。

表5　针织物弹性模量与拉伸角度的非线性回归方程

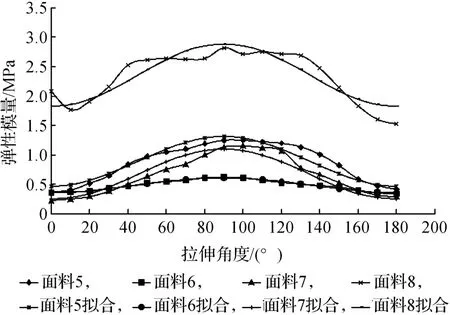
图6　针织物弹性模量—拉伸角度的变化关系

根据实验曲线波形特征，进一步通过SPSS非线性回归分析，可得到这4种针织物弹性模量—拉伸角度曲线的回归方程（见表5）和三角函数拟合曲线（见图6）。

3　机织物和针织物拉伸各向异性变化规律的探讨

根据实验中对机织物和纬编针织物的拉伸性能的测试和模型分析可以从中发现一定的规律性。观察面料3的拉伸曲线拟合公式ε=0.110+0.062× sin，并结合三角函数的波形规律，可以看到常数项0.110和三角函数的振幅0.062分别是有一定实际含义的。如果将θ=0°和45°分别代入拟合公式，就可以求得常数项0.110=，振幅0.062=。因为从拉伸曲线图上可以看出面料3经纬向拉伸应变是相近的，所以对于具有对称的组织结构并且在一定负荷下拉伸，经纬向的拉伸应变相近的织物，其拉伸应变随着角度的变化规律可以总结为：

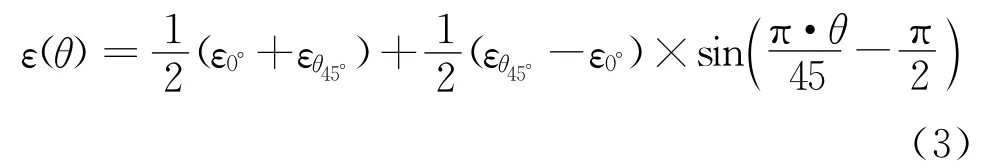
式（3）对经纬向拉伸应变相近并且具有组织结构对称性的机织物的各个角度拉伸性能预测具有重要意义。其实只要测试织物纬向（或经向）和45°角的拉伸性能再结合式（3）就可以计算出织物任意拉伸角度的拉伸应变值。

观察面料1、2和4的拉伸曲线拟合公式，运用同上的代入法，能够找到类似的规律。因为面料1、2和4都是相同负荷下经纬向拉伸性应变不同的机织物，所以这类织物拉伸应变随着角度的变化规律可总结为：

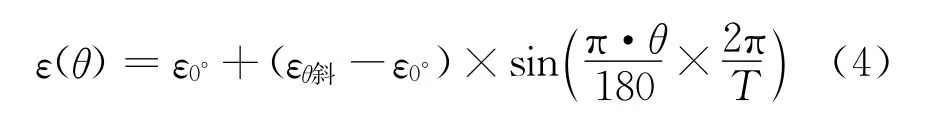
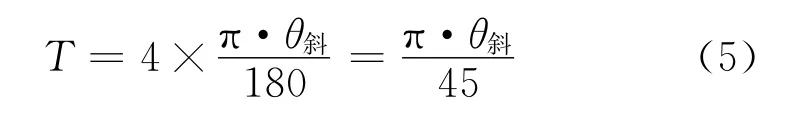
观察面料5、6、7和8，用同样的代入法，可以发现它们代表的纬编针织物拉伸应变随拉伸角度变化的规律可以总结为：

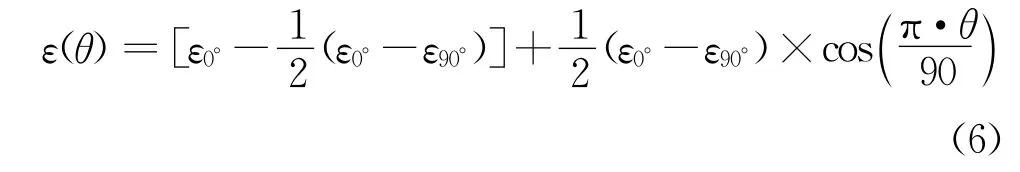
化简后即为

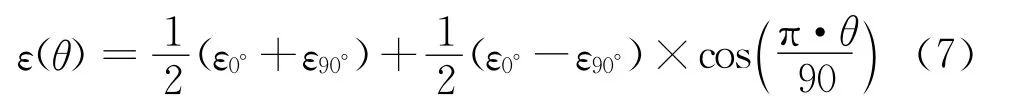
如果用θ＇表示θ角度对应的弧度，公式（7）最终化简为：

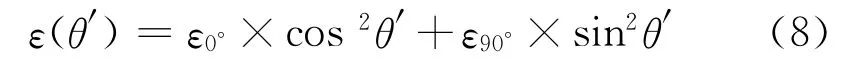
式（8）刚好满足了弹性力学中材料斜向（不考虑切应变）的应变公式（其中εx和εy以及α分别表示材料沿x轴和y轴方向的应变以及斜向与x轴的夹角），针织物的这一表现可能是因为其具有较大的弹性，因而也就更加符合弹性体的这个模型。由此可见公式（8）对于纬编针织物各个角度的拉伸性能预测具有重要意义，实际中只要测试织物纬向和经向的拉伸应变，然后利用式（8）就可以计算出纬编针织物任意拉伸角度的拉伸应变值。

上述分析可以说已经揭示了织物各个角度拉伸性能中特殊角度和任意角度之间的内在联系和规律。在测试某几个特殊方向拉伸性能的基础上，可以运用式（3）、式（4）和式（8）来预测不同织物拉伸应变随角度变化的情况。这使得我们在实际的织物的拉伸性能测试和预测中能够达到窥一斑而知全豹的效果，可以提高相关测试和工作效率。

4　结论

本文主要研究服用织物在低应力下拉伸的各向异性行为，结果有：

a）机织物的拉伸应变曲线近似双波峰的三角函数曲线，一般经向和纬向拉伸时，应变处于曲线低谷，斜向拉伸时应变增大，在45°和135°附近会出现拉伸应变的最大值。

b）纬编针织物的拉伸应变曲线呈中间下凹形状，试样均在0°或180°（纬向）时应变最大，在90°（经向）时应变最小。

c）机织物中，斜纹布1的弹性模量曲线，在0～180°呈现较有规律的三角函数波形曲线特征；平纹布1、平纹布2和斜纹布2的弹性模量曲线在60°～120°呈现单波峰的曲线形状，而在其它区间弹性模量值的变化较为平缓。

d）与机织物不同，4种纬编针织的曲线形状在0～180°呈中间凸起的波峰形状且波形图的形态相近。

e）各织物的拉伸应变、拉伸模量与拉伸角度间的三角函数拟合方程，均具有较高的拟合优度。可以运用相应的公式来计算预测其拉伸应变随角度变化的情况，特别是针织物拉伸性能的预测公式与弹性力学中材料斜向的应变公式具有高度一致性。

［1］张芝兰，李文璋，张亚莹.机织物各向异性力学性能的研究［J］.天津纺织工学院学报，1992，11（2）：1-7.

［2］李 焰，谭 磊.服用机织物力学性能各向异性的分析［J］.纺织学报，2003，24（2）：118-120.

［3］洪维亚，龙海如.罗纹针织物双向拉伸性能测试分析［J］.纺织科技进展，2009（6）：57-59.

［4］谭 磊，胡心怡.拉伸方向对针织物断裂强力和断裂伸长的影响［J］.天津工业大学学报，2001，20（5）：53-55.

［5］徐 军，姚 穆.织物弯曲刚度各向异性的探讨［J］.西北纺织工学院学报，2001，15（2）：102-104.

［6］倪 红，潘永惠.基于BP神经网络的织物斜向弯曲性能的预测［J］.纺织学报，2009，30（2）：48-51.

［7］朱柳静，吴巧英，高雪莲.轻薄丝织物斜向力学性能及缝纫缩皱研究［J］.丝绸，2010（3）：20-23.

［8］Kristina D，Eugenijia S.Influence of layer orientation upon textile systems tensile properties part 1：investigation of tensile strain and resilience［J］. Materials Science，2006，12（1）：73-78.

［9］Kristina D，Eugenijia S.Influence of layer orientation upon textile systems tensile properties part 2：investigation of tensile energy and linearity［J］. Materials Science，2006，12（3）：247-252.

［10］糜庆丰.各向异性织物建模与仿真［D］.杭州：浙江大学，2011：15-31.

［11］徐芝纶.弹性力学［M］.北京：高等教育出版社，2006：15-20.Anisotropic Analysis of Fabric Tensile Property

PAN Yuea，CEN Jiea，YOU Xiao-yuea，YANG Yun-chua，b
（a.School of Fashion Design and Engineering；b.Zhejiang Provincial Research Center of Clothing Engineering Technology，Zhejiang Sci-Tech University，Hangzhou 310018，China）

In this paper，Instron3344 tester is used to test tensile properties of 4 woven fabrics and 4 weft knitted fabrics in order to master the influence of different tensile directions on tensile properties under low stress.The main contents include：establish a curve graph between tensile strain and elasticity modulus and describe their change rules；use nonlinear regression in SPSS system to create fitting equations between tensile strain，elasticity modulus and stretching angle.The results show：woven fabrics and weft knitted fabrics have different curve characteristics in terms of anisotropic tensile behaviors，and all fitting equations of trigonometric function have high goodness of fit.

fabric；tensile properties；anisotropy；nonlinear regression

TS101.2

A

1673-3851（2015）06-0733-05

（责任编辑：张祖尧）

2014-12-09

浙江省自然科学基金项目（LQ12E05015）；浙江理工大学教育教学改革研究项目（jgyl1403）

潘 月（1990-），女，江苏南京人，硕士研究生，研究方向为织物服用性能分析。

杨允出，E-mail：gary0577@zstu.edu.cn