双圆弧谐波齿轮设计及性能仿真
袁安富,林 森,仲霞莉
(1.南京信息工程大学 信息与控制学院,南京 210044;2.江苏省气象能源利用与控制工程技术研究中心,南京 210044)
0 引言
针对目前国内制造业自动化转型,我国将成为全球工业机器人最大的市场。作为机器人的核心传动部件,谐波减速器将担当着举足轻重的地位。采用渐开线齿形谐波齿轮,柔轮和刚轮只是近似共轭[1],大多数齿均为边缘啮合或尖点啮合,这种啮合受力不均匀,轮齿容易磨损,而且载荷过大时容易造成齿与齿之间的干涉。而圆弧齿廓同时啮合的齿数更多,运动精度更高,柔轮的疲劳强度也得到很大提高。
1 谐波减速机结构形式[2]
谐波减速机中柔轮的结构一般分为圆柱型和钟形,本文主要分析圆柱形柔轮,轴连方式为凸缘外向的螺钉连接。波发生器结构众多,本文采用标准椭圆凸轮波发生器,这种波发生器可以使柔轮与刚轮的啮合达到理想状态,运转平稳,精度高,效率也较高。椭圆凸轮波发生器装入柔轮后,柔轮变形如图1所示,1表示柔轮变形前,2表示柔轮变形后。谐波减速器基本结构为:波发生器作为输入部件,刚轮作为固定部件,柔轮作为输出部件。

图1 柔轮变形图
图1中w为柔轮的径向位移,w0为柔轮长轴处的最大变形量,rm是柔轮变形之前的半径,ρr是原始曲线的极半径。
2 柔轮齿形设计及基本方程的建立[3~5]
2.1 柔轮齿形设计
根据圆弧齿轮的设计经验,对于精滚调质的软齿面圆弧齿轮,一般取全齿高h为2m~2.25m,其中m是模数。为了避免柔轮与刚轮轮齿之间的干涉,需要留有一定的顶隙,因此双圆弧齿廓谐波齿轮传动柔轮基准齿形齿高h可初步定为1.8m~2.12m, 柔轮齿顶高ha可以取为0.7m~1.0m,齿根高hf为1.1m~1.5m,取齿顶间隙Wa为0.2m~0.35m。齿形角取为25°。双圆弧谐波齿轮柔轮基本齿廓设计如图2所示。

图2 柔轮基本齿廓
2.2 柔轮齿廓方程的建立
根据图3所示,首先建立轮齿坐标系,以柔轮轮齿的的对称线为坐标xoy的y轴,以柔轮的中性线为该坐标的x轴,以齿廓的右边为例。
柔轮凸齿廓的圆心移距量X1为:
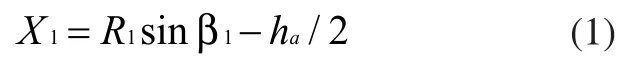
凸齿廓的圆心偏移量L1为:
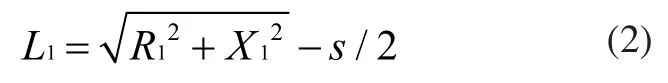
柔轮右侧凸齿廓的极坐标方程为:

其中,t为柔轮的壁厚,β1为凸齿廓的压力角,(XO1,YO1)为凸齿廓的圆心坐标。
柔轮右侧凹齿廓极坐标方程为:

式中,X2和L2分别为柔轮凹齿的圆心移距量和偏移量,为凹齿廓的压角,为凹齿廓的圆心坐标。
3 根据包络法求解刚轮理论啮合方程
3.1 建立坐标系
设一个固定坐标系(OXY)与波发生器相固连,Y轴与波发生器的长轴重合,原点O定于波发生器的圆心上,两个动坐标系(O1X1Y1)和(O2X2Y2)分别与柔轮和刚轮相固连,Y1轴与柔轮轮齿的对称轴相重合,O1位于柔轮的中线上。Y2与刚轮齿槽的对称轴线重合,O2位于刚轮的回转中心上。各个坐标系之间的关系如图3所示。
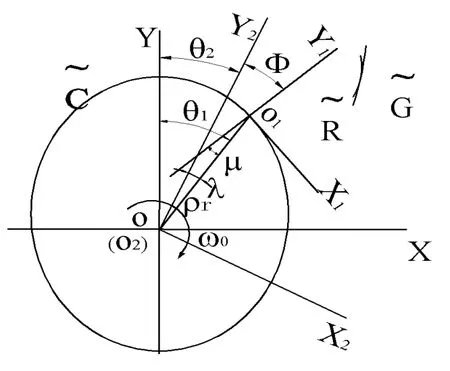
图3 包络法求共轭齿形时各坐标关系图
图中,θ1为柔轮特征曲线对应弧的转角,θ2为刚轮特征曲线对应弧的转角,λ为刚轮与柔轮对应弧中心角之差。μ为柔轮对称轴线相对于径失转过的角度,Ф为刚轮和柔轮两个坐标系的夹角。
3.2 各参数之间的关系
如图4所示,原始特征曲线的极坐标方程为:

式中,θ为柔轮非变形端的转角。
使用包络法求解刚轮齿形时其他各关系表达式为:
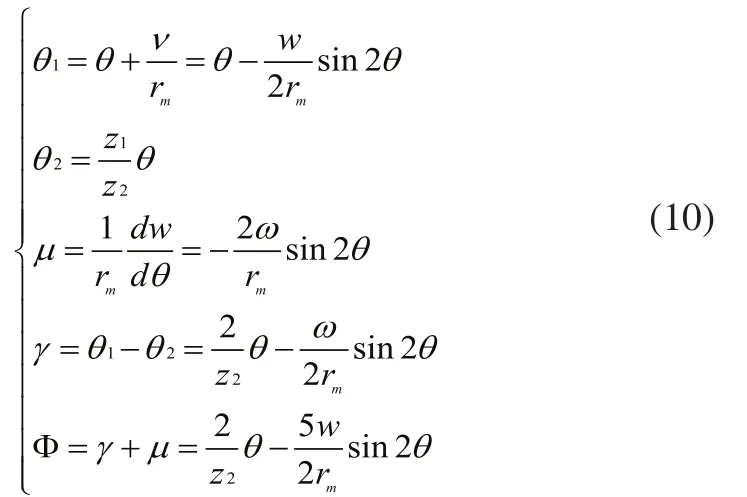
3.3 刚轮齿廓方程的建立
使用包络理论求解与柔轮共轭的刚轮齿廓基本方程为:

将柔轮凸齿廓AB段的方程(3)代入到式(11)中即可求得与其共轭的刚轮齿廓方程为:将柔轮凹齿廓CD段方程(6)代入到式(3.4)中即可求得与其共轭的刚轮齿廓方程为:
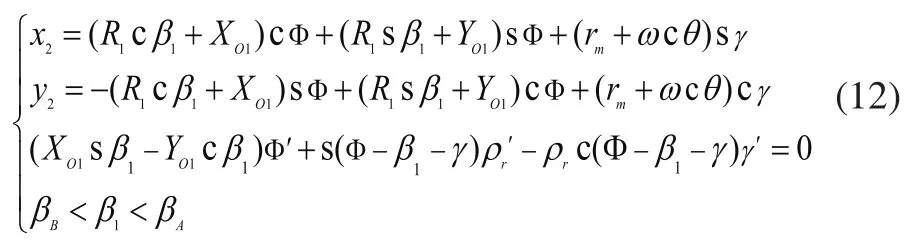

其中各偏导数分别为:

公式中的c代表cos、s代表sin。
4 实例分析
以传动比i=80的的谐波齿轮为例,采用双波传动,柔轮齿数Z1=160,刚轮齿数Z2=162,模数m=0.5,柔轮变形系w*=0.9,柔轮轮齿处壁厚为1m,光滑处壁厚为0.8m,柔轮凸齿廓的圆心移距量X1=0.19m、偏移量L1=0.71m,圆弧半径R1=1.09m,柔轮凹齿廓的圆心移距量X2=0.26m、偏移量L1=1.54m,圆弧半径X2=1.2m,波高为0.5,通过计算得出柔轮的齿顶圆为Φ81,齿根圆为Φ78.9,刚轮的齿顶圆为Φ80,齿根圆为Φ82.1。
使用三维软件UG,分别对柔轮、刚轮以及波发生器进行建模,添加装配约束,其具体装配图如图4所示,从图中我们可以看出,柔轮在波发生器的挤压作用下发生指定的变形,在长轴处,柔轮齿顶和刚轮齿顶处如设计一样,能够进入完全啮合状态,且有一定间隙,以防止轮齿间干涉,在短轴处,柔轮及刚轮轮齿能够完全脱开,互不干涉。与传统的渐开线齿形相比,双圆弧齿形啮合的齿对数更多。

图4 谐波齿轮装配图
5 对柔轮进行有限元分析[6,7]
5.1 有限元模型的建立
由于在谐波齿轮的设计过程中,我们已经使用三维软件对柔轮完成了建模,因此,将UG建立的柔轮模型以parasolid格式导出,再将此文件导入到ANSYS中。对柔轮材料参数进行设定:E=196GPa、泊松比μ=0.3。
5.2 网格划分
考虑到柔轮变形较大,所以选择solid185作为划分模型的基本单元,他能够用于模拟塑性、应力刚化、蠕变、大变形、大应变等场合。柔轮变形部位主要集中在轮齿处,所以对轮齿部位要划分的更精细一些,这样结果也就更准确,使用体分割的办法将轮齿和筒体进行分割,然后再分别对它们进行网格划分,划分后的模型如图5所示。

图5 柔轮网格划分模型
5.3 定义接触及添加约束
柔轮与波发生器的接触可以定义为刚—柔接触,接触方式为面—面接触,以柔轮的内壁为柔性面,以波发生器的外圈为刚性面。定义好接触对后,会自动生成TARGET170和CONTACT174两种接触单元。
由于所设计的减速器中,柔轮与箱体是螺栓连接,因此将柔轮底部的内缘定义为完全约束ALL DOF=0。
5.4 结果分析
柔轮的径向变形如图6所示,其最大变形量主要集中在长轴处,且对称分布,最大变形值为0.517m,接近设计时的理论波高0.5m。柔轮的整体变形如图7所示,由于在波发生器的短轴处,柔轮要向内收缩,所以也产生了一定的变形,而对于整个柔轮筒体,随着筒体远离轮齿,它的变形量也逐渐减小。

图6 径向位移

图7 整体位移
柔轮的应力云图如图8所示,其应力主要集中在长轴附近,且靠近与轮齿和光滑筒体的交界处,而柔轮的短轴处所受应力最小。将轮齿部位的应力云图进行放大后查看,如图9所示,发现应力主要集中在轮齿的齿根处,因此,柔轮的疲劳断裂将会首先从齿根处逐步向外延伸。
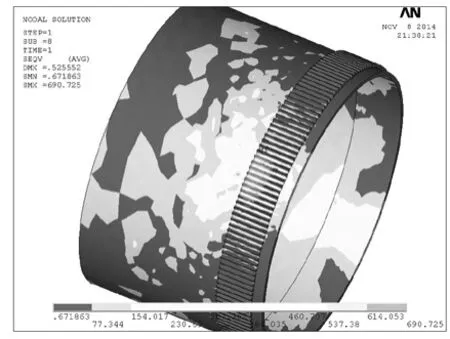
图8 应力云图

图9 局部放大图
6 结束语
本文通过三维软件UG对设计好的双圆弧谐波齿轮三大部件进行建模和装配,针对齿轮啮合顶隙、侧隙、啮合深度及啮合齿对数等多个方面,分析得出设计的合理性,并与渐开线齿形相比,双圆弧谐波齿轮同时啮合的齿数更多。
基于有限元分析软件ANSYS,对波发生器装入后的柔轮进行仿真分析,通过应力应变云图,得知柔轮的径向最大位移量与理论波高基本一致,其应力主要集中在波发生的长轴处及轮齿及光滑筒体的过渡处,在成功预测其危险断面的同时,为以后柔轮结构的优化设计提供一定理论依据。
[1] 毛彬彬,王克武.谐波齿轮的齿形研究和发展[J].煤矿机械,2008,29(7):6-8.
[2] 沈允文,叶庆泰.谐波齿轮传动的理论和设计[M].北京:机械工业出版社,1985.
[3] 辛洪兵.双圆弧谐波齿轮传动基本齿廓设计[J].中国机械工程,2011,22(6):652-662.
[4] Xiaoxia Chen,Yusheng Liu, Jingzhong Xing, Shu zhong Lin , Wei Xu . The parametric design of double-circular-arc tooth profile and its inf l uence on the functional backlash of harmonic drive[J].Mechanism and Machine Theory,2014,73:1-24
[5] 范元勋,王华坤,宋德峰.谐波齿轮共轭齿廓的运动学仿真研究[J].南京航空航天大学报,2002,34 (5):487-450.
[6] Oguz , Kayabasi, FehmiErzincanli. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modeling [J]. MaterialsandDesign,2007,28:441-447.
[7] 邱勇,胡晓兵,赵彦植.基于ANSYS的柔轮应力与应变有限元分析[J].机械制造,2012,5(576):14-16.

