强噪声背景下基于振动信号分析的齿轮故障诊断

李宏宇，程 刚，陈曦晖，胡 晓

（中国矿业大学 机电工程学院，徐州 221116）

0 引言

齿轮传动是煤矿机械最重要的传动方式，齿轮发生故障会导致机器工作效率降低，甚至严重事故[1]。因此，及时发现和诊断齿轮故障具有重要意义。利用振动信号对齿轮进行故障诊断是一种有效手段。

在强噪声背景下有用信息都被噪声淹没，如何从非平稳的振动信号中提取出故障特征信息是齿轮故障诊断的关键。针对强噪声背景，可利用小波阀值降噪原理对含噪信号进行降噪，得到信噪比较高的有效信号。获得有效信号后，故障特征的准确提取是关键，由于煤矿机械所处环境复杂，振动信号受诸多因素影响，利用传统的时、频域特征提取方法已不能准确反映齿轮工作状态。将EEMD和样本熵方法相结合可形成一种适用于提取非平稳信号的故障特征信息提取方法。EEMD分解可将齿轮振动信号分解为若干IMF分量，并可有效的抑制EMD中的模态混叠[2]。同时齿轮在发生不同故障时，各IMF分量的样本熵会发生改变。基于此，本文提出结合小波阀值降噪、EEMD熵特征的故障特征信息提取方法，并通过概率神经网络来对齿轮故障进行识别，验证所提方法的有效性。

1 诊断模型建立

1.1 小波阀值降噪原理

小波阀值降噪的实质是综合特征提取和低通滤波两者的功能，我们实测的信号一般是低频或较平稳的信号，而噪声信号往往是高频信号。对信号降噪就是抑制信号无用部分增强有用部分的过程[3]。

小波阀值去噪方法具有多分辨率、去相关性、选基灵活的特点，其中最为关键的是小波基和阀值规则的选取，这将决定信号去噪的质量。

1.2 EEMD熵特征

1.2.1 EEMD

EEMD利用了高斯白噪声具有频率均匀分布的统计特性，当信号加入白噪声之后，将使信号在不同尺度上具有连续性，以减小模态混叠的程度。其具体步骤和原理如下[4]：

1）在降噪后的信号x(t)中加入幅值具有均值为0，标准差取信号标准差0.3倍的白噪声ni(t)，则：

式中，i为xi(t)分解次数。

2）对xi(t)进行EMD分解，得到若干IMF分量cij(t)与1个余项ri(t)。其中cij(t)为第i次加入高斯白噪声后，分解得到的第j个IMF。

3）重复步骤1和步骤2N次。得到消除模态混叠的IMF为：

信号EEMD分解的最终结果为：

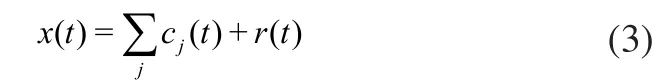
式中：r(t)为最终的残余分量，代表信号的平均趋势。

1.2.2 样本熵

样本熵是用来刻画时间序列复杂程度，反应时间序列维数发生变化时产生新模式的概率，以及时间序列在模式上的自我相似度。可很好地用于机械振动信号的分析[5]。

计算时间序列样本熵的步骤为[6]：

1）对于一个拥有Nt个点的数据序列x(1),x(2),…,x(Nt)可以组成一组m维的矢量：

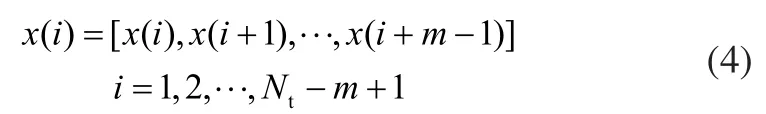
2）定义两个m维的矢量X(i)和X(j)之间的最大距离为：

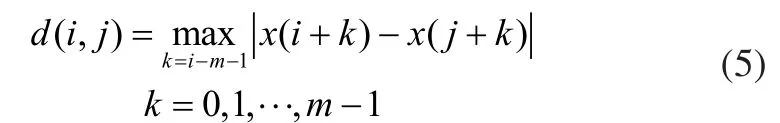
3）对于给定的阀值r，从1～Nt-m+1计算(,)d i jr＜的数目除以的值，记为，即：

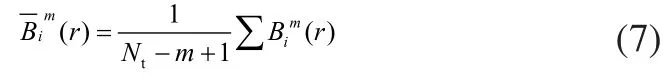
1.3 PNN神经网络

PNN神经网络是基于Bayes分类规则与Parzen窗的概率密度函数估计方法发展而来的一种并行算法，在解决分类问题方面得到了广泛应用[7]。

在实际应用中，根据输入特征向量构建合适的PNN网络，初始化网络后，利用训练样本对网络进行训练，训练结束后将测试样本输入到网络进行识别并输出结果。其诊断识别流程如图1所示。

图1 概率神经网络识别流程图

2 实验装置及信号采集方式

齿轮故障诊断实验在美国Spectra Quest公司的机械故障综合模拟实验台上进行，该实验台配备了齿面磨损与断齿等故障。本文主要对齿轮正常、齿面磨损、断齿和少齿四种状态进行实验，每种齿轮状态采集50个样本，共200个样本。通过对所采集信号进行分析，检验所建立的故障识别方法。

实验采样频率设置为10kHZ，样本长度为15000，电机的转速20Hz。用加速度传感器测取振动信号的原始数据。四种齿轮状态下采集的原始振动信号如图2所示。

图2 原始振动信号

从图2可以看出断齿齿轮的振动信号呈现明显周期，但是其他三种齿轮的振动信号没有明显区别。

3 实验过程及分析

由于篇幅限制，仅以断齿故障状态为例进行分析，对断齿故障信号进行小波阀值降噪处理。为模拟强噪声背景，人为加入随机高斯白噪声，信噪比设置为0.5，采用db5小波对含噪信号进行6层分解。分解结果如图3所示。

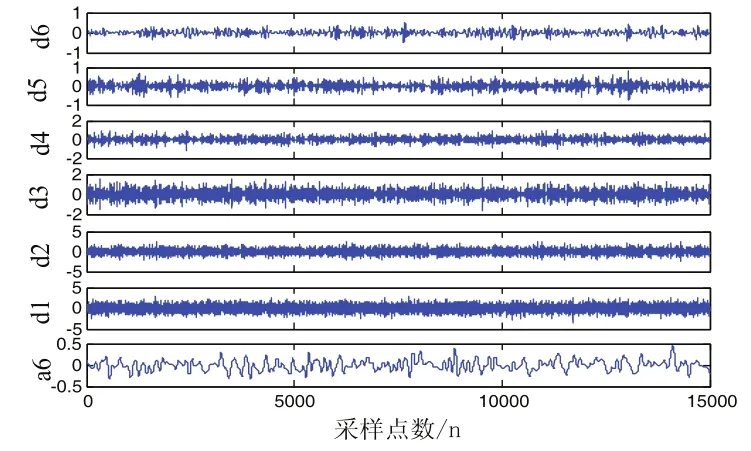
图3 断齿信号小波分解

其中a6表示信号的近似部分，d1-d6表示信号的高频部分，为了消除外界干扰噪声，采用启发式阀值heursure对各高频系数进行降噪处理，再进行小波重构，降噪前后图形对比如图4所示。

图4 断齿信号降噪前后对比

由图4可见，加入噪声后，原始信号完全淹没在噪声中，对其进行小波阀值降噪之后，噪声得到了明显的消除，周期性更加明显。

对降噪后的信号进行EEMD分解，确定噪声与原始信号幅值标准差比值为0.3，平均运算次数为100次，得到EEMD分解结果，如图5所示。

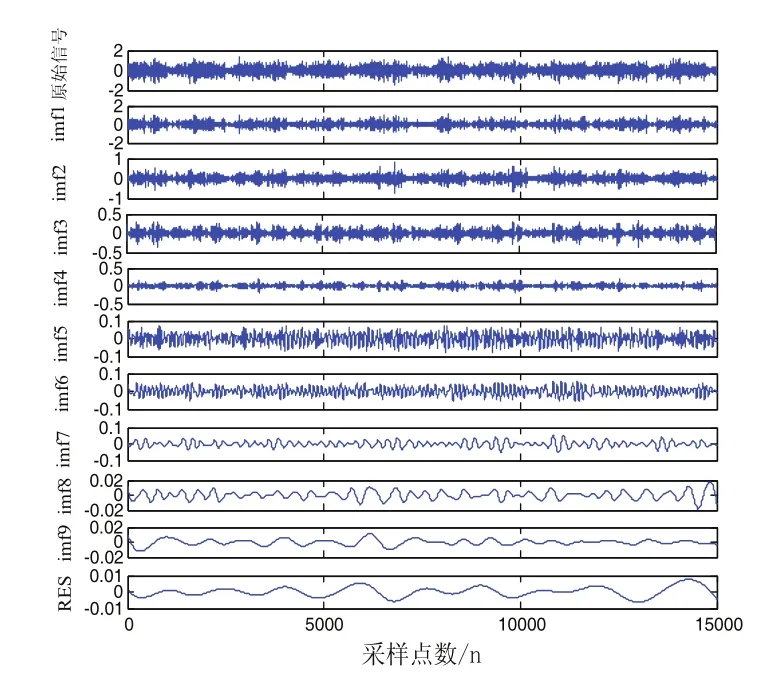
图5 降噪后断齿信号EEMD分解结果

可见，断齿齿轮的信号被分解成9个IMF分量和一个残项。考虑到齿轮故障特征频率集中在中高频，取前3个IMF分量进行样本熵计算，可以获得需要的特征信息。计算时选择嵌入维数m为2，相似容限r为0.2。

限于篇幅，文中只列出了每种齿轮状态的三组样本熵值，如表1所示。

由表1可以发现，故障齿轮的样本熵值均大于正常齿轮，说明设备发生故障时，样本熵值有明显的变化，区别于正常状态。但仅根据样本熵还不能得到准确的故障类型，故以概率神经网络作为分类器，进行故障诊断识别。

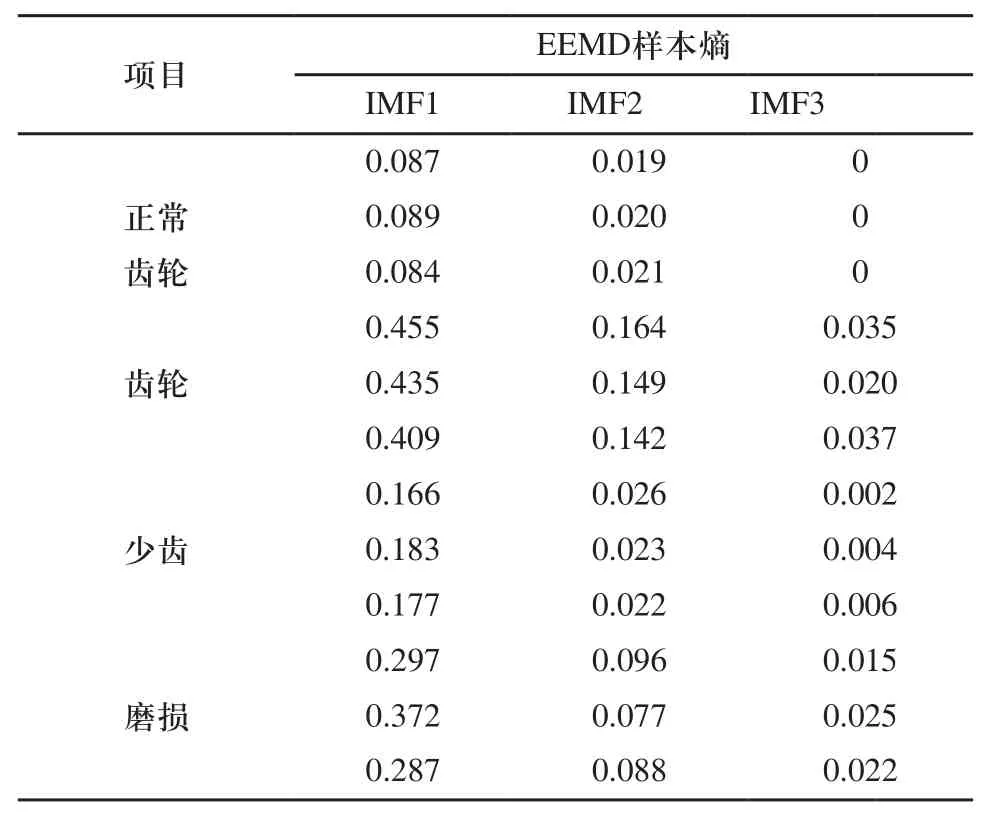
表1 四种齿轮状态下的EEMD样本熵

将样本熵作为概率神经网络的特征向量，取每种状态中的30个样本，共120个组成训练样本，其余80个样本作为测试样本，用以验证识别模式的有效性。预测结果如图6所示。

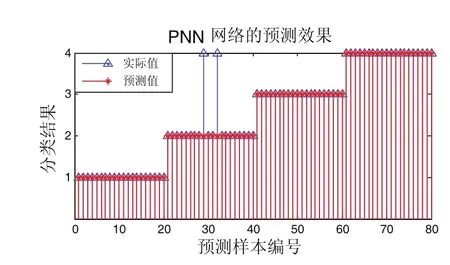
图6 PNN网络预测效果

观察图6可以发现，在类别1中，即齿轮正常状态，识别率为100%；在类别2中，即断齿状态，有2个错误识别，识别率为90%；在类别3中，即少齿状态，识别率为100%；在类别4中，即磨损状态，识别率为100%。由此可见识别率最低的为断齿故障，识别率为90%，但总体识别率仍达到97.5%。

4 结束语

本文提出的强噪声背景下基于振动信号分析的齿轮故障诊断方法，对含噪的原始信号进行小波阀值降噪，利用EEMD自适应地将降噪后的信号分解成若干结构简单的IMF分量，选择前3个IMF分量的样本熵构成故障特征向量，结合概率神经网络进行故障模式识别。实验结果表明，该方法对4种齿轮状态总体识别率达到97.5%，适用于处理强噪声背景下齿轮故障产生的非平稳信号，能够实现齿轮故障的准确识别。

[1] 白亚红.基于EMD和SVM技术风电齿轮箱早期故障诊断研究[D].大连:大连理工大学,2009.

[2] 李亮.基于样本熵和模糊聚类的轴承故障诊断方法研究[D].秦皇岛:燕山大学,2011.

[3] 刘尚坤,唐贵基,庞斌.小波降噪与Hilbert解调相结合的齿轮故障诊断方法[J].制造业信息化,2014,103(04):103-104.

[4] 秦娜,金伟东,黄进,李智敏.基于EEMD样本熵的高速列车转向架故障特征提取[J].西南交通大学学报,2014,49(01):27-31.

[5] 胡晓,钱沛云,陈曦晖,程刚.基于多尺度熵-BP神经网络的采煤机摇臂齿轮故障诊断[J].制造业自动化,2014,36(09):4-7 .

[6] 楼军伟,胡赤乐,赵家黎.EEMD样本熵在轴承故障SVM识别中的研究[J].机械传动,2014,38(03):41-43.

[7] 陈波.基于粗糙集-概率神经网络结合的变压器故障诊断研究[D].南宁:广西大学,2008.