基于粒子群算法的光伏MPPT控制策略研究

马运亮，高梅峰，周超超

（1.许继电气股份有限公司，许昌 461000；2.许昌供电公司，许昌 461000）

0 引言

面对日益严峻的生态环境污染和化石燃料短缺的困境，积极发展可再生能源，走可持续发展的道路是社会发展的必由之路。光伏发电作为新型可再生能源，有着众多优点，例如阳光充足、分布广泛、持续性好，将来无疑会成为一种最理想的替代能源[1]。然而光伏发电本身还存在若干问题，其中最大功率点跟踪便是光伏发电系统相关技术的研究热点之一。

在光伏发电系统中，用来实现MPPT控制有很多典型的算法[2]，其中应用最广泛的有恒定电压法、干扰观测法和电导增量法。文献[3]中介绍了恒定电压法的基本原理，但是该方法追踪到的最大功率点并不是真正意义上的MPPT，而是一个接近值，而且该算法受温度的影响较大。文献[4]中介绍了干扰观测法的应用，但是该方法实时性不好，在光照强度发生快速变化的时候，输出特性曲线也会发生很大的变化，而且在这个过程中很有可能发生错误的判断；文献[5]介绍了相比前两种方法更有效的电导增量法，但是该算法和前面两者一样均不能解决局部阴影情况下的最大功率跟踪问题。

针对传统算法的局限性本文将群体智能领域中的粒子群算法应用到光伏发电MPPT控制系统中。该算法对于存在全局最优和局部最优的复杂非线性问题，求出全局最优解的概率高，并且最后直流侧电压工作于稳定值。其并行处理的方式加快了系统的收敛速度，算法简单，鲁棒性好，易于工程实现。

1 粒子群算法基本原理

粒子群算法（Particle Swarm Optimization, PSO）是一种基于迭代的优化算法起源于对鸟群觅食过程的模拟[6]。将搜索最大食物源的鸟称为“粒子”，每个粒子的位置都是一个解，最终系统将收敛至最优解。在粒子每次迭代过程中，每个粒子的位置和速度可由以下公式描述[7]：

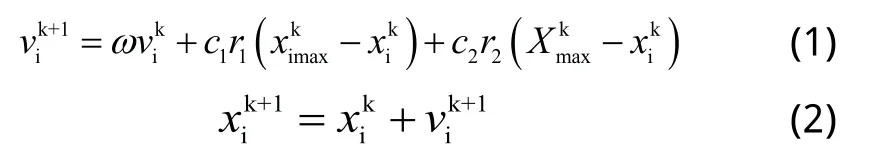
式(1)和式(2)中，i=1,2,…,m。m为粒子的个数，k为迭代次数，ω为惯性权重系数，c1，c2为常数，r1和r2为0～1之间的随机数。定义ximax为第i个粒子的历史最优值位置，Xmax为整个粒子群的最优解所在位置，f为问题的目标函数，即衡量粒子所在位置优劣的适应度函数。在迭代过程中，ximax和f(Xmax)分别为：

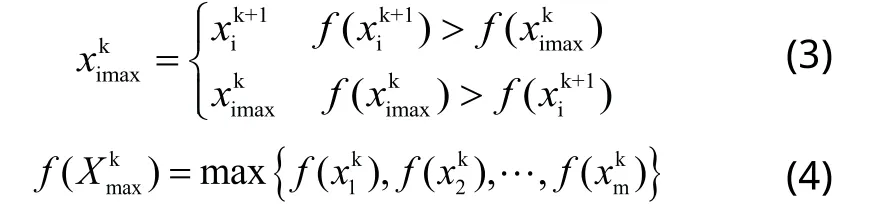
惯性权重系数ω使粒子根据自身速度作惯性运动，反映了粒子的记忆功能。c1和c2使粒子具有学习调整功能，用于分配个体经验和群体经验影响个体收敛速度的比重，粒子在搜索过程中逐渐向最优值靠近。r1和r2使得粒子在搜索过程中具有随机性，以更大的概率趋近最优解。该式的目标是计算粒子的行进方向和速度，所包含的三个部分分别为动量部分、认知部分和社会部分，体现了粒子群算法的智能性和可行性。

2 基于粒子群算法的MPPT控制

根据光伏电池的输出特性，在一定约束条件下将粒子群算法的执行流程和算法的参数设计方法应用到光伏发电系统中最大功率跟踪控制。在最大功率点跟踪过程中，直流侧电压给定值Vdc为粒子位置xi，光伏电池输出功率值P为粒子位置优劣的衡量标准，为第i个粒子在第k次迭代后光伏阵列输出电压，为第i个粒子在第k次迭代后光伏阵列输出电流，则目标函数为：

光伏并网系统中，可按照以下步骤对求解过程进行约束和参数选择：

1）首次搜索采取固定间隔遍历法。搜索域为光伏并网逆变器直流母线电压正常工作范围与光伏电池正常工作输出电压范围的交集，由于电池阵列的串并联方式取决于逆变器功率等级和并网电压，所以搜索域Vpvf主要取决于逆变器系统参数，其维数为1且。

2）在最优解搜索过程中，光伏阵列输出特性曲线是随时间变化的，而粒子群算法认为整个搜索过程中光伏阵列输出特性基本不变，为了避免陷入局部最优，时间步长越小越好，本文采用搜索点时间间隔变步长法。

3）搜索终止条件与重启条件取决于光伏阵列特点和外界自然环境特点。考虑实际系统所需精度，可将搜索终止条件限制在一个较小范围内，本文按照式(6)所示条件。

搜索终止后系统稳定运行于最大功率点Pmax处。在外界自然环境变化后，MPPT算法应当重启。

4）粒子的最大速度vmax决定粒子群在解空间所搜的力度，vmax越大，粒子的探索能力越强，但容易越过最优解。vmax越小，粒子群的开发能力越强，但陷入局部最优时，很可能使粒子无法移动足够远的距离跳出局部最优，同样不能搜寻到系统全局最优解，并且其对全局最优解的搜索时间可能会更长。

5）结合仿真调试，对于惯性系数ω本文取定值0.25以使得粒子保持一定惯性向最优解处移动。为了提高对最大功率点的跟踪速度，学习因子r1取2，r2取3。

3 仿真及实验分析

为验证基于粒子群算法的光伏MPPT控制策略的可行性，在MATLAB仿真平台及实验平台上对上述方案进行验证。仿真中采用两组光伏电池板并联，每组由12块串联。给予两组光伏电池不同的光照和温度，出现多个峰值的情况。光伏阵列的I-V特性和P-V特性如图1(a)和图1(b)所示，从图中可以看出，光伏阵列存在两个峰值，一个峰值在全局最大功率处，电压约为360V，最大功率约为4kW，另一个峰值在局部最大功率处，电压和功率分别为425V、2.5kW。

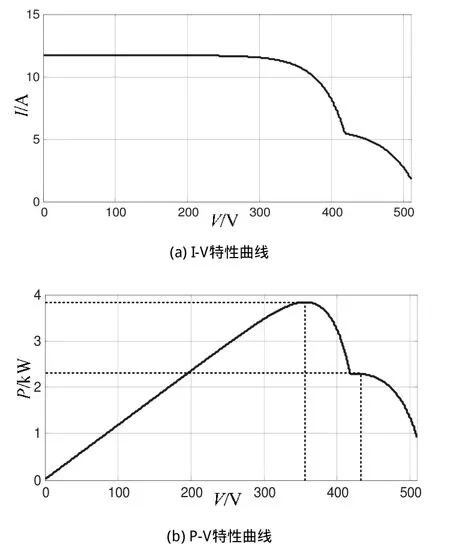
图1 不均匀条件下输出特性

采用基于变步长扰动观察法计算得到的电压参考值与光伏阵列输出功率如图2(a)和图2(b)所示。由图可知，随着直流侧电压降低，输出功率在增大，但直流侧电压经过425V时，扰动观察法认为该峰值为最大功率点，输出功率为2.3kW。

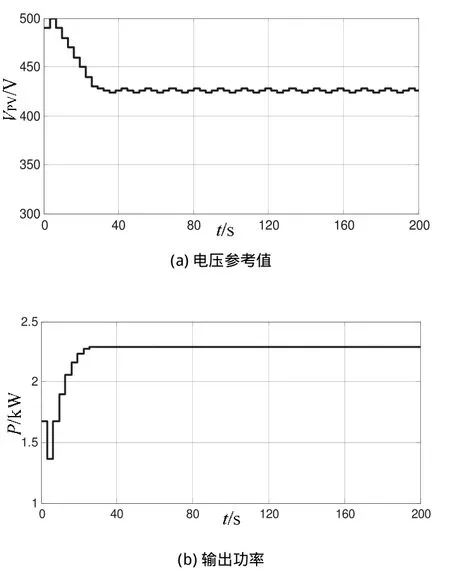
图2 扰动观察法仿真结果

基于粒子群算法计算得到的电压参考值与光伏阵列输出功率如图3(a)和图3(b)所示。从图中可以看出，该方法并非以寻找功率峰值为目标，而是以寻找全局最优解为目的，经200s后系统直流侧电压工作在全局最优点360V左右，输出功率为3.8kW左右，仿真结果证明了所采用方法的有效性和优越性。

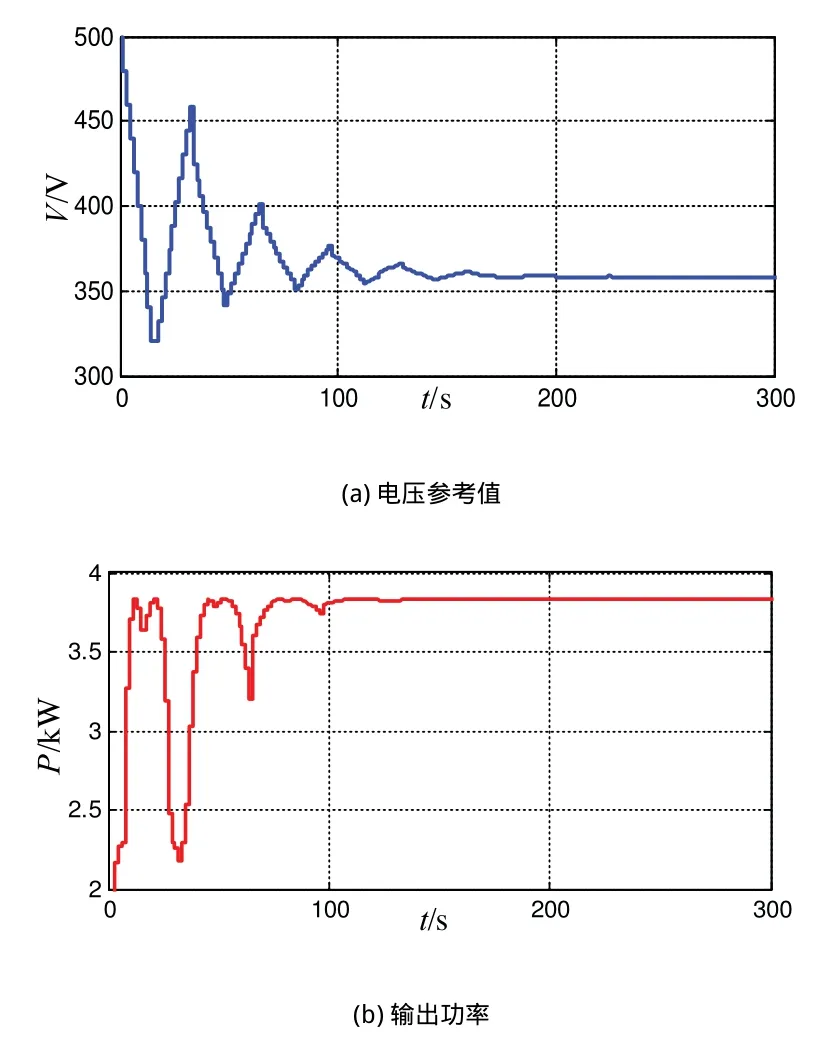
图3 粒子群算法仿真结果

基于DSPTMS320F28335搭建了基于粒子群算法的光伏MPPT控制实验平台。

实验样机中光伏阵列开路电压为520V，光伏阵列端口电压、电流、输出功率如图4所示。从图4中可以看出，最大功率点在420V左右，约为开路电压的0.8倍，与理论分析相符，随着电压的下降，越过最大功率点后，光伏阵列输出功率逐渐减小，功率变化趋势与光伏电池特性曲线相同。

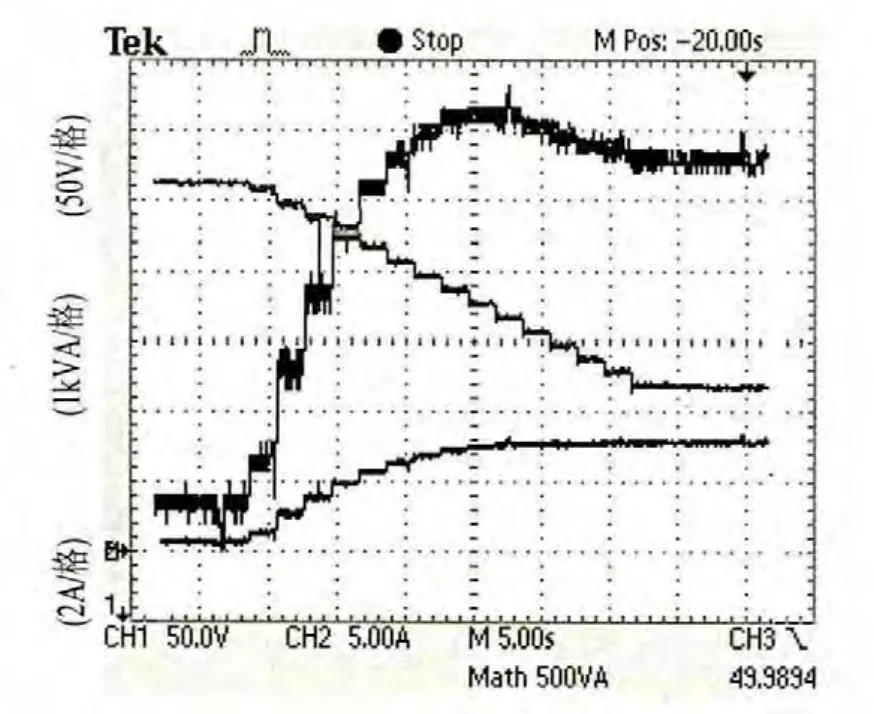
图4 光伏阵列端口输出特性波形

光伏并网工作状态下，变流器启动阶段最大功率跟踪波形如图5所示。从图中可以看出，变流器从开路电压520V启动后，随着电压在搜索域内扫描，输出电流和功率随着电压的波动而波动，最终稳定在最大功率点电压425V左右，最大功率点电流约为9A，输出功率约为4kW，该功率值也与第一个扫描周期出现的最大功率相等，验证了MPPT算法的正确性和可行性。

4 结论

本文利用粒子群算法在解空间中对全局最优解的搜索原理，定义光伏发电最大功率跟踪控制系统中直流侧电压给定值为粒子位置变量，光伏电池输出功率值为粒子位置优劣的衡量标准变量，构造目标函数利用粒子群算法实现不均匀条件下的MPPT跟踪。最后基于MATLAB/SIMULINK软件的仿真分析及实验结果证明了该方案的有效性与可行性。

[1] 高志强,王建赜,纪延超,谭光慧,张举良.一种快速的光伏最大功率点跟踪方法[J].电力系统保护与控制,2012,08:105-109.

[2] 高金辉,唐静.一种新型光伏系统最大功率跟踪算法的研究[J].电力系统保护与控制,2011,23:21-24+29.

[3] 邱培春,葛宝明,毕大强.基于扰动观察和二次插值的光伏发电最大功率跟踪控制[J].电力系统保护与控制,2011,04: 62-67.

[4] 陈剑,赵争鸣,袁立强,查澜曦.光伏系统最大功率点跟踪技术的比较[J]. 清华大学学报(自然科学版),2010,05:700-704.

[5] 汤济泽,王丛岭,房学法.一种基于电导增量法的MPPT实现策略[J].电力电子技术,2011,04:73-75.

[6] 朱艳伟,石新春,但扬清,李鹏,刘文颖,魏德冰,付超.粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用[J].中国电机工程学报,2012,04: 42-48+20.

[7] 李天博,褚俊,陈坤华.基于粒子群算法的MPPT仿真及应用[J].电力电子技术,2012,01:7-9.