读懂学生

波利亚曾说：“教师讲什么固然重要，但学生想什么比这重要一千倍。”这就需要教师用敏锐的眼光，捕捉剖析学生平淡、稚嫩、精彩，亦或错误的回答背后隐藏的思想，站在同一思维频道上，解读学生思维，进而激起学生思考，跟进教学行为，成就课堂的精彩。

读懂学生情感，等待自省，唤醒思维认知

小学生是情感丰富的个体，只有读懂了学生的情感，教师才会真正了解学生，明白他们“因何而起”“何以如此”。

《分数的初步知识》课上，笔者请部分学生在黑板上用画图的方式诠释“一半”这个概念，目的是为后面让学生认识分数产生的价值作铺垫。学生按照自己的想象，画出了不同的1/2图。

分析引出1/2的概念之后，笔者看着一开始到黑板上表示“一半”的学生，用商量的口吻说：“我想和你们商量一下，刚才你们画的图、线段和文字都表示把这个物体平均分成两份，表示这样的一份。如果你认为1/2这个分数能表示你的意思，就可以擦掉你画的；如果你认为你的表现方法更好，也可以保留意见。”很多学生纷纷跑上去擦掉自己画的图、文字、线段。只有一名学生坚持认为自己画的图更好，执意不擦，笔者并没有强求，而是尊重了他的意见，并把这幅桃子图框起来保留在黑板上。

最后，笔者请学生结合生活实际，用分数说一句话。学生甲：“我家有3口人，我占全家人口的1/3。”学生乙：“我们组有7个人，我们组的人数占全班人数的7/50。”……当一个学生说道“我爸爸买了100个鸡蛋，打碎了1个，打碎了的正好占这些鸡蛋的1/100”时，笔者顺手将1/100写到了黑板上，并特意把开始上课时坚持用画图方法表示分数的那名学生请上来，“1/100该怎样用你喜欢的画图方法表示呢？请你试试看！”只见这名学生认真地画着，画着画着停住了，他扬起小脸：“老师，这种方法太麻烦了，还是分数表示好。”边说边使劲把开始画在黑板上的桃子图擦掉，看来他是真的体会到分数的价值，心服口服地接纳了分数这个新朋友。这时笔者握着这个孩子的手微笑着说：“感谢你，你终于接受了分数。”

读懂学生思维，搅动平衡，直击知识本质

学生思维是否活跃和活跃到何种程度，是评价一堂课成功与否的重要标尺。课堂就要设计有效的教学活动，激发学生思考，让学生思维充分动起来。

课上，学生4人一组围桌而坐。桌面上摆放着水杯、可乐瓶、圆形纸片、刻度尺、绳子和剪刀。

师：龙潭湖公园有一个圆形花坛，为了保护花草，准备沿花坛围一圈篱笆，需要多长的篱笆呢？你们能帮助解决这个问题吗？请用手中的工具，小组合作探索圆周长的计算方法。

（话音一落，学生立刻合作起来，非常积极地探索各种方法。过了一会儿，小组代表开始发言。）

生1：我们小组是把圆形纸片立起来放在刻度尺上滚动一圈，就测出了它的周长。

师：如果有一个很大的圆形水池，要求它的周长，能用你们小组的方法把水池立起来放在刻度尺上滚动一圈吗？

生2：我们研究了一个好方法。先用绳子在水池周围绕一圈，再量一量绳子的长度，不就是水池的周长了吗？

师：好！好！这的确是个不错的方法！”

（停顿片刻，笔者拿出了一端系有小球的线绳，在空中旋转了一圈，又旋转了一圈。）

师：小球走过的痕迹形成了一个圆，要想求这个圆的周长，还能用你们的办法吗？

（学生摇摇头，再次陷入沉思。）

生3：我们又发现了一种求圆周长的方法。将这张圆形的纸对折3次，这样圆的周长就被平均分成了8段，我们测量出每条线段的长度是2厘米，8段是16厘米，也就是圆的周长。

师：很有创意！你们用折纸的方法求出这个圆的周长，很了不起。但是用滚动的方法、绳绕的方法以及折纸的方法只能求出某些圆的周长，都有局限性。我们能不能探索一条求圆周长的普遍规律呢？

学生的思维又活跃起来，把对圆周长的探索推向了一个新的高潮。经过学生探索，规律找到了，学生沉浸在成功的喜悦当中。

读懂学生困惑，构建平台，理解内化知识

学生困惑的地方往往是教学的难点、着力点，也是知识的生长点，思想方法的渗透点。读懂困惑要“知其因，晓其果”，为学生的理解搭建平台 。

一起看笔者讲的《重叠问题》一课的片段：

笔者在黑板上贴上语文组和数学组，找两名学生在黑板前对号入座。女生完成语文组，男生完成数学组。

语文组 数学组

1 2 3 4 5 6 7

8 9 10

师：一起数一数语文组有几人？

（生齐数3人。）

师（对完成的女生）：语文组同意吗？

生1：不同意。

师：怎么办？那赶快抢啊！

（女生把4号和5号移动到自己处。）

师（问男生）：你们呢？

（男生又抢了回去。）

师：这样抢下去可不行，怎么办？怎么解决4号和5号呢？谁有主意？

生2：再写一个4和5。

语文组 数学组

1 2 3 4 5 6 7

4 5 8 9 10

师：行不行？

生3：不行。

师：还看不出语文组有5个人，怎么办？

生4：放中间。

师：行不行？试试。

（生4把4、5号放在中间。）

师：怎样能一眼看出来。谁有招？

生5： 语文组 数学组

1 2 3 6 7

8 9 10

↖ ↗

4 5

师：我们看懂了，就是4号和5号可以是语文组，也是可以数学组的。

师（指前面排队问题的圈圈）：我们可以借助前面的经验啊！

（生5把语文组、数学组用集合圈圈起来。）

语文组 数学组

师：这次给他的掌声热烈一些。

师：独立思考一下，看图，你能写出怎样的算式？

（教师巡视，找几种不同方法的学生进行板演。）

（板书：5+5+2=12 5+7-2=10 3+2+5=10 5+7+2=14 ） 之后笔者引领孩子们结合图分析算式，错——错在哪里，对——讲出道理。重叠问题的本质就是在一次次图与算式、算式与算式的勾连中明晰的。

最后，笔者带领孩子们深入分析。

师：现在是两人重复。还有可能几人重复？

生1：3人、4人、5人、6人、7人、8人。

生2：嗯？

师：为什么“嗯”？

生2：不可能有8人重复，最多5人重复。

师：我们一起看一看，会有一人重复吗？怎么表演？

（两名学生上前把一个点遮住。）

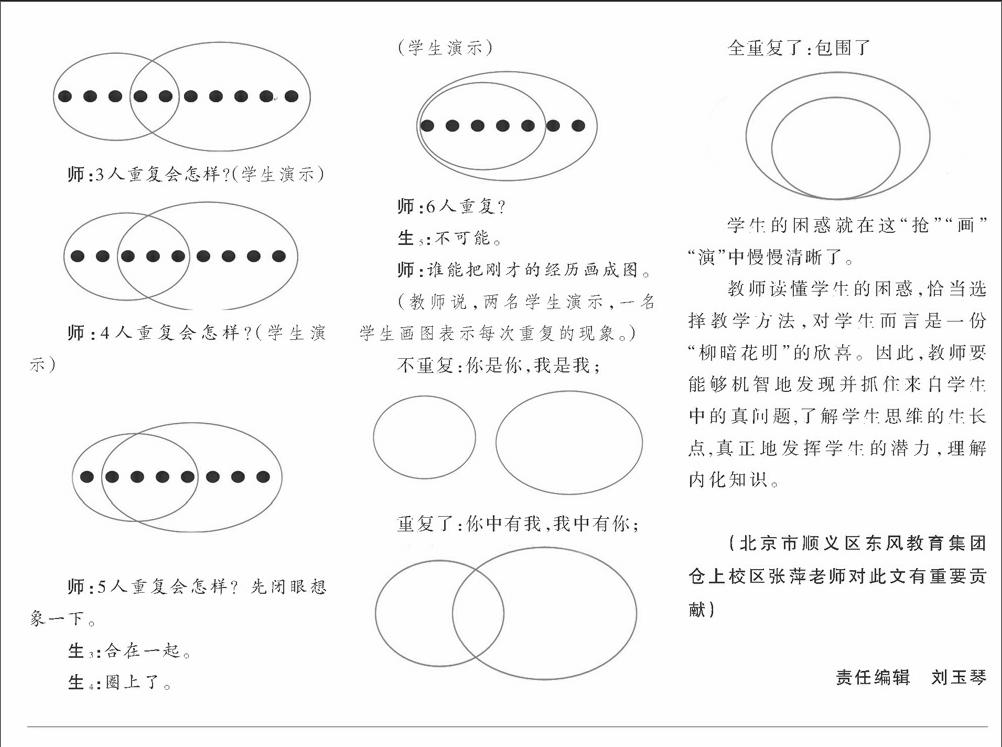
师：想象两人重复会怎么样？（学生演示）

师：3人重复会怎样？（学生演示）

师：4人重复会怎样？（学生演示）

师：5人重复会怎样？先闭眼想象一下。

生3：合在一起。

生4：圈上了。

师：6人重复？

生5：不可能。

师：谁能把刚才的经历画成图。

（教师说，两名学生演示，一名学生画图表示每次重复的现象。）

不重复：你是你，我是我；

重复了：你中有我，我中有你；

全重复了：包围了

学生的困惑就在这“抢”“画”“演”中慢慢清晰了。

教师读懂学生的困惑，恰当选择教学方法，对学生而言是一份“柳暗花明”的欣喜。因此，教师要能够机智地发现并抓住来自学生中的真问题，了解学生思维的生长点，真正地发挥学生的潜力，理解内化知识。

（北京市顺义区东风教育集团仓上校区张萍老师对此文有重要贡献）

责任编辑 刘玉琴