数学解题中诱发学生分类讨论的七种因素
刘家良
能否依照一条“主线”对问题进行合理分类是衡量学生思维条理性及严谨性的试金石.在初中阶段,具有哪些因素的问题能诱发学生的分类讨论呢?对此,笔者归纳了诱发学生分类讨论的七种因素,旨在引导学生思考与分类有关的问题时能找出问题中的一条“主线”作为标准进行分类,合理取舍,力求使各种可能的结果做到不重不漏,以此逐步养成学生的分类讨论意识,培养学生思维的条理性和严谨性.
一、边(角)指代不明诱发的分类
某些图形中的边(或角)的大小虽已知,但具体是哪条边(或哪个角)指代并不明确.对此先将边(或角)归类,再依据定义或定理求解.
例1 等腰三角形的一条边长为6,另一边长为13,则它的周长为( ).
(A)25 (B)25或32 (C)32 (D)19
分析:长为6和13的两边,没有明确“谁”是等腰三角形的底边和腰,所以先需将“6”归类(分别为底边和腰)再求三角形的周长.但注意当6为腰时,则其他两边为6, 13,因为 6+6<13,所以6,6,13不能构成三角形,应舍去.故应选C.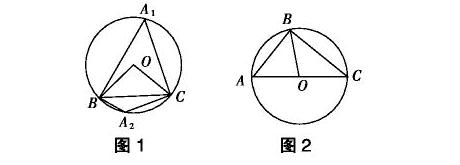
例2 一个直角三角形的两边长分别为6和8,则该三角形中较小锐角的正弦值为 .
分析:长为8的边虽在已知边中较长,但没有明确出它是直角边还是斜边,对此先需对“8”归类(分别为直角边和斜边).结果为:或.
中等生和学困生在解答边(或角)指代不明的问题中,常常会丢掉其中的一种可能情况.对此,教师需将具有种属和并列关系的概念“串”在一起,通过比对,寻找异同点,澄清模糊点,做到准确理解概念内涵,把握概念外延.在批改作业中,在“隐藏”分类的关键字眼处用“字符边框”的方式圈注进行提示,如例2中可将 “两边长”圈注,提醒学生应分类思考.
二、图形间相对位置关系不明朗诱发的分类
图形之间的相对位置关系若在已知条件中不明朗,则需先列出所有可能的位置关系,再分情况逐一求解.
例3 已知△ABC的外心为点O,若∠BOC=100°,则∠A的度数为 .
分析:△ABC与其外心O的位置关系存在三种情况:当△ABC为锐角三角形时,其外心O在形内;当△ABC为钝角三角形时,其外心O在形外;当△ABC为直角三角形时,其外心O在斜边上.而这三种情况都有可能,如图1,图2.结果为:50°或130°.
【注】多数学生只想到外心在三角形内部而忽视了外心在三角形外和一边上的情形.对此,教师在作业讲评时,要让学生逐一按锐角三角形、钝角三角形和直角三角形画出三角形的外心,明确三种情况,在理解外心定义中,融入了分类意识.
三、对应关系不明确诱发的分类
三角形的全等或相似的判定和性质都体现了“对应”思想.所以在已知图形全等或相似的前提下解边(或角)的问题时,需要突出边(或角)的对应关系.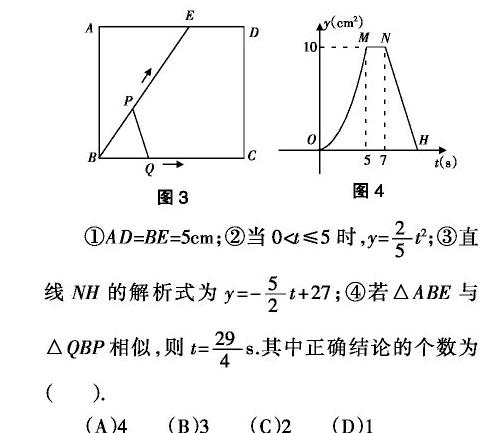
例4 两个三角形相似,一个三角形的三边长分别为,,2,另一个三角形的两边长分别为1,,则它的第三边长为 .
分析:已知三角形的三边按从小到大的顺序排序为,,2,.设所求三角形的第三边长为x,因为两个相似三角形中边的对应关系不明确,所以需将x的取值需分三种情况:x<1,1
【注】虽然有部分学生也得到了问题的答案,但是没有分类的一种“巧合”.对此类问题要树立对应思想,形成思维问题的有序性.
四、“动”——诱发图形量变或形变的分类
这里,“动” 指图形大小(或形状)变化的同时其相应图象也随之发生变化.解这类问题时,要学会“阅读”图象,既要分“段”破译,又要将“段”与“段”综合在一起通盘思考.对此要挖掘每段图象所蕴含的信息量和“段”与“段”之间“折点”的信息,将形与数的结合与转换思想融入其中.
例5 如图3,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图4(曲线OM为抛物线的一部分).则下列结论:
①AD=BE=5cm;②当0 (A)4 (B)3 (C)2 (D)1 分析:从图4中看出△QBP的面积变化呈现出三个特征:综合图象前2段的信息(5s时△QBP的面积最大且持续2s面积都不变),对照图3,知P,Q出发5秒时,点P到达点E,同时点Q到达了点C,从而得到BC,BE的长度;在第2段图象中,对照图3,点P从点E到点D中,用时2s,可得ED,AE的长度.在第3段图象中,对照图3,点P从点D到点C中,△QBP的面积逐步减小,直至为0. 解:根据图4中前2段的信息,结合图3,知当点P到达点E的同时点Q到达了点C.因为点P,Q的运动的速度都是1cm/s,所以BC=BE=5,AD=5.当0
【注】根据图4判断出点P到达点E时,点Q到达点C是解题的关键,是本题的切入点.
五、式、方程、函数内涵不具体时诱发最高项系数为0和非0的分类
当一个式、方程或函数中的最高项系数是含有字母的式子且式、方程或函数的“名称”不明确时,需对含字母的式子是0和非0进行分类.
例6 已知函数y=mx2-6x+1(m是常数).若该函数的图象与x轴只有一个交点,求m的值.
分析:最高项的系数为m,而函数没有明确一定是二次函数,所以需对m为0和非0的情况进行分类.①当m=0时,函数y=-6x+1的图象与x轴只有一个交点(,0);②当m≠0时,y=mx2-6x+1为二次函数.因为函数的图象与x轴只有一个交点,所以二次方程mx2-6x+1=0有两个相等的实数根.所求m的值为0或9.
解这类问题时需要学生先仔细读题、审题后再下笔.教师在“究因”中,要将易混的相关概念通过学生比较寻找出异同点,同时结合解题抠字眼的过程进一步明晰概念的内涵.
六、双曲线“分支”描述诱发的分类
反比例函数y=(k≠0)的图象为双曲线.对同一个k值,其增减性应分“象限”考察,就是说,同一个k值,同一个象限内两点的纵坐标的大小可以按“增减性”去判断,但在两个分支上的点就不能按“增减性”去判断了.
例7 一次函数y1=kx+b(k≠0)与反比例函数y2=(m≠0),在同一直角坐标系中的图象如图6所示,若y1>y2,则x的取值范围是( ).
(A)-2 (B)x<-2或0 (C)x<1 (D)-2 分析:由图6知,一次函数与反比例函数相交于点(-2,-2),(1,4).当-2 本题考查了一次函数、反比例函数的图象性质及学生读图能力,旨在让学生注意到反比例函数的“增减性”是“分支”(分象限)考察的. 七、“规则”呈现动态诱发的分类 某些应用题的“规则”呈现出“动态”性,则相应的计算法则也随之发生了变化. 例8 某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案: 方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款). 方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元). (1)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式. (2)小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢? (3)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法. 分析:(1)购买者购买的楼层x有可能高于第八层,也有可能低于第八层,而两者的购房方案不同.故此需将x分大于8和小于8两种情况讨论. (2)因为小张购房采用方案一,故只需求出小张按这种方案付款的算式,需按照高于第8层和低于第8层两种情况来进行(承接第一问);无论购置哪一个楼层,小张付款金额都不会大于120000元,由此产生了不等关系. (3)判断老王自想的法则和方案二哪一个购房更划算,需先求出各自对应的付款算式.因为方案二中的算式中含有字母a,无法直接比较二者大小,故应采用逆向思维的方法分类来解. 解:(1)当2≤x≤8且x是正整数时,y=3000-(8-x)×20=20x+2840;当9≤x≤23且x是正整数时,y=3000+(x-8)×40=40x+2680. (2)由(1),知①当2≤x≤8时,因为最贵的是第8层,首付款为:3000×120×30%=108000元,小于120000元,所以小张可从2~8层中任选一层;②当9≤x≤23时,由(40x+2680)×120×30%≤120000,得x≤16.因为x为正整数且9≤x≤23,所以小张用方案一可以购买二至十六层的任何一层. (3)若老王按方案二购买第十六层,则要实交房款为w1=(40×16+2680)×120×92%-60a(元).若按老王自想的法则要交房款为w2=(40×16+2680)×120×91%(元).w1-w2=3984-60a.当w1>w2时,得0 【注】(1)分类求函数式是一个从特殊归纳出一般规律的探究过程.(2)“120000元”购置楼房,不论购买哪一层,有可能出现剩余,也有可能用尽.(3)逆向性分类(由结论找条件),展现了思维的灵动性. 以上列举了诱发学生分类讨论的七种因素,只不过是抛出了一块“砖”(分类的形式、内容)而已,从中如何引出一块玉(分类的意识和思想)是笔者撰文的归宿点.在教学中让学生体验具有种属关系概念的分类原则(如有理数、实数的分类),从解有关“分类”的习题(如动点、圆、相似三角形)中主动寻找分类的“主线”.久之,分类的意识、思想就会逐步生成. 

