问题探究需要怎样的探究?
朱玉祥
最近给学生讲题,讲了一道探究类的题目.该题的结构是:先问题探究,给出两个小问题让学生解决;然后题锋一转,就进入问题解决,给出一个真正需要解决的问题.显然,给出的问题一定和前面的两个小问题相关,或是解决问题的方法相关,或是从小问题中获得的结论相关,或是把前面小题的探究作为起点,迁移到新问题中继续探究.笔者常把此类题目比喻成撑竿跳高,前面小题是热身,是辨向,是起步,是助跑,而真正要解决的问题是放置在高处的横竿,能不能跃过横竿,先要看热身、辨向、起步、助跑后一竿撑起的高度.高度有了,才有跃过横竿的可能.所以,解决此类题,笔者告诫学生,一定要让自己通过解决前面小题有一竿“撑”起来的感觉,然后抓住这个感觉向横竿飞跃.当然,此类题如果小题设置得过于特殊,要靠小题“撑”对方向,“撑”出高度,还是有难度的.
讲这道题时,课堂上就出现“辨向”错误,从小题的解决中,似乎得到了“经验”,似乎“撑”起了高度,但“撑”错了方向,结果离“竿”远了,解决问题也就出现了错误.接着纠错,重新调整方向,再次“撑”起一竿,最终问题得到解决.从出现错误到纠正错误的过程中,学生明白了一个道理:特殊问题中获得的经验可能仅仅在特殊情况下有用,要向一般化迁移,要继续作一般化的探究.也就是说,不要被特殊化的结论所迷惑,必须要继续探究问题的本质.否则,题目中具有“引导性”的小问题很可能把我们拖入问题解决的“歧途”.下面就来说说这道题解题教学过程中的一些问题与思考.
一、思维阻滞
(一)原题呈现
问题探究 (1)请在图1①中作出两条直线,使它们将圆面四等分;
(2)如图1②,M是正方形ABCD内一定点,请在图1②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.
问题解决 (3)如图1③,在四边形ABCD中,AB∥CD,AB + CD=BC,点P是AD的中点.如果AB=a,CD=b,且b>a,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.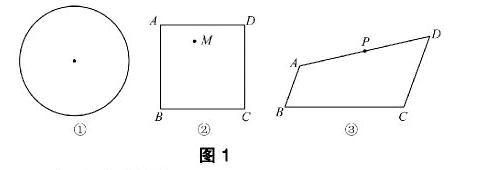
(二)尝试解答
上课时,先把题目发给学生,让学生尝试解答.
学生看到题(1)和题(2)比较兴奋,认为太容易了,几乎没经过思考,就开始画图.有的学生一边画图还一边说,这么容易做的题竟然放在压轴题中,真不敢相信.
可以看到,学生都能在图1①中画出两条互相垂直的直径;在图1②中,很多学生也知道先找正方形ABCD对角线的交点O,然后画出直线OM,最后再过点O画出与直线OM垂直的另一条直线.在题(1)与题(2)的解答中,学生并没有遇到太大困难.
但进入题(3),学生不说话了,压轴题对他们的挑战开始了.笔者巡视中看到,有学生过点P画AD的垂线(见图2),就问:这条直线能平分四边形ABCD的面积吗?为什么这样画?学生摇摇头,说,可能不对.但题(1)与题(2)不就是这样分的吗?显然,学生一边觉得自己画的直线PQ可能不对,一边又觉得从题(1)、题(2)的垂直分割“经验”看好像又只能这么画.问题是,学生既不能说明直线PQ可以把四边形ABCD分割成面积相等的两部分的理由,也不知道如何求出BQ的长度.问题解决的思维受阻.
(三)难点分析
问题探究的两个小题应该是问题解决的起点.但两个小题选取的图形都非常特殊,一个是具有旋转不变性的圆,一个是集平行四边形、矩形与菱形的所有性质于一身的正方形,把它们分割成面积相等的四部分,思考方法几乎不用变化,都是经过它们的对称中心做互相垂直的直线.学生在画图的时候,甚至都没有任何“探究”,只是基于“经验”,就想得到,做得出.正是因为起点比较低,没有经历必要的“探究”,解决题(3)就有困难.
解决题(3)的困难有三.一是由中心对称图形变成非中心对称图形,题(1)、题(2)的经验难以迁移过来;二是从画两条直线把所给图形分成面积相等的四部分,变成画一些直线,把所给图形分成面积相等的两部分,不知道前后问题有什么关联;三是转化的困难.学生很难想到把图1③通过旋转转化成中心对称图形,再借鉴题②的经验去思考问题的解决.
困难的关键,是学生对题(1)、题(2)探究不够.没能从特殊到一般深入地探究.所以,讲题时,要考虑到以上难点,并设计相应的教学环节,给学生以引导.
二、重回问题探究
(一)小题之间的关联
笔者告诉学生,当问题解决思维受阻的时候,不妨重回问题探究,看探究的两个问题与要解决的题(3)有什么可以关联的知识和方法.
探究题(1)、题(2)所给的两个图形都是中心对称图形,那么,题(3)所给的图形是不是也能转化成中心对称图形?研究图1③,因为点P是AD的中点,把四边形ABCD绕点P旋转180°,旋转前后的图就可以拼成一个中心对称图形,点P为对称中心.
继续探究.题(1)、题(2)用两条直线把所给图形的面积四等分(两条直线都过图形的对称中心),如果沿着其中一条直线剪开来,取其一半,题目就改变成用一条直线把一半图形面积两等分,这样,题(1)、题(2)就和题(3)在要解决的问题上比较接近了.
图3是题(1)取其一半后的图.对半圆,过AB的中点O用一条直线把它两等分,只有唯一的方法,即作OC⊥AB.图4是题(2)取其一半后的图.过EF的中点O用一条直线把它两等分,也只有唯一的方法,即作OG⊥EF.那么,题(3)会不会也有唯一的方法,会不会如图2那样作PQ⊥AD?endprint
(二)换一个角度考虑
题(1)探究的是圆,题(2)探究的是正方形,为什么这两个图形的两条四等分线都要过它们的对称中心,并且相互垂直呢?圆很好解释,因为只能画两条直线,所以必须过圆心;因为分成的四部分都是扇形,所以扇形的弧长必须相等,于是每一个扇形的弧长恰是圆周的.当然,扇形的弧所对的圆心角就是90°,所以,两条四等分直线相互垂直.也就是说,过圆心的两条直线四等分圆面,把圆周四等分是关键.
正方形呢?如图5,要保证分割成的每一部分都是正方形ABCD面积的,那么,S四边形EBGO=S△OBC,所以S△OEB=S△OGC,又因为正方形的对称中心O到正方形的四边距离相等,所以,EB=GC.事实上,过正方形对称中心O画两条直线把正方形面积四等分,若与一组邻边AB,BC交于点E,G,那么只要EB=GC或AE=BG即可.此时对正方形而言,EF与MG也互相垂直.但垂直不是本质,过正方形对称中心的两条直线把正方形的周长分成四等分是关键.
(三)一般化探究
之所以说“垂直”不是本质,是因为过对称中心的两条互相垂直的直线并不一定能把该图形的周长四等分,也就未必总能把所给图形四等分.不妨来看菱形.
如图6,在菱形ABCD中,AC,BD交于点O,则点O到菱形ABCD的四边距离相等.过点O任作直线EF⊥HG,分别交AB,BC,CD,AD于点E,G,F,H,显然,要想S四边形EBGO=S△OBC,必须S△OEB=S△OGC,所以必须BE=CG才行.可是,EF⊥HG并不能保证有BE=CG.所以,过对称中心的两条垂直的直线只能把圆和正方形的面积四等分(也能把偶数边的正多边形的面积四等分),不能把菱形的面积四等分.
通过上面的分析,可以得到较为一般化的结论:如果中心对称图形的对称中心到各边(圆周可以看作圆的边)距离相等,那么把该图形面积四等分的两条直线必须同时满足:一要过该图形的对称中心,二要能四等分该图形的周长.所以说,过对称中心的两条直线能等分周长才是四等分面积的本质.
(四)进一步思考
如果中心对称图形的对称中心到各边的距离不相等,那么面积四等分线如何分其周长呢?以矩形为例.
如图7,在矩形ABCD中,AB=a,BC=b,点O为对称中心,OM⊥AB,ON⊥BC,垂足分别为M,N,过点O的直线EF,GH分别交AB,BC,CD,AD于点E,G,F,H,那么,OM=b,ON=a.要想由直线EF,GH把矩形ABCD的面积四等分,那么必有S四边形EBGO=S矩形ABCD.连接OB,设BE=x,BG=y,则有S△OEB+S△OBG=S矩形ABCD,即·x··b+·y·a=ab.所以,有bx+ay=ab.即直线EF,GH四等分矩形ABCD,必须满足条件bx+ay=ab.当a=b时,矩形ABCD即为正方形ABCD,此时x+y=a.
换一个角度.事实上,由于点M是AB的中点,点N是BC的中点,要满足S四边形EBGO=S矩形ABCD,只要满足S四边形EBGO=S矩形MBNO即可,此时只要S△OME=S△ONG,所以有ME·b=NG·a,所以=,所以BE=x=a-ME,BG=y=b+NG,直线EF,GH才能四等分矩形ABCD.当a=b时,矩形ABCD即为正方形ABCD,此时ME=NG,所以BE+BG=a.
可以看到,四等分线如何分矩形的周长,应与矩形的邻边比值相关.即中心对称图形的对称中心若到各边的距离不等,那么,四等分该图面积的两条直线分其周长应与对称中心到各边距离的比值相关.
三、问题解决
从“问题探究”到“问题解决”,不是说只解决题(1)和题(2)的问题就算“问题探究”了,还需要根据“问题解决”中的问题需要,将“问题探究”中的问题继续作一般化探究.比如解决了用两条直线将圆和正方形的面积四等分后,还要继续探索用两条直线四等分菱形面积的条件,甚至探索两条直线四等分矩形面积的条件,然后再进入问题解决.当然,由于题(3)给的图形1③是菱形的一半,那么由题(1)和题(2)作为引子,继续对菱形进行探究是必不可少的.
回到题(3).因为AB∥CD,AB + CD=BC,点P是AD的中点,将四边形ABCD绕点P旋转180°得菱形C′BCB′(如图8),所以存在直线AD和PQ将菱形C′BCB′的面积四等分,点Q在BC上,此时,CQ=AB=a,BQ=CD=b.由此可得,在BC上存在点Q,且当BQ=b时,PQ所在直线将四边形ABCD的面积分成相等的两部分.
四、点滴教学感悟
(一)探究不能流于表面
问题探究类的题目总是先给出一些小问题(或特殊问题)探究.这个时候,探究不能止于所给问题,还需要看探究的问题与要解决的问题之间还有多大的间隔,有多少阻碍.探究需要缩小间隔,排除阻碍.比如,探究的问题比较特殊,而要解决的问题又趋于一般化,之间相隔着一般化的认识与探究,就需要把探究的问题延展引申,做一般化的研究,拉近与要解决的问题之间的距离.
(二)探究的一般方法
探究类问题解题的一般方法就是化归思想方法.化归就是转化并归结.比如在经历过“问题探究”环节后,积累了一定的问题解决经验,获得了问题解决的一些方法,那么,对“问题解决”中需要解决的问题就可以向“问题探究”中的问题转化,或者归结到“问题探究”中的已经解决的问题类型中,用探究获得的方法和经验解决新问题.
(三)关注探究的起点
问题探究实际上是给问题解决提供解题的起点.在“问题探究”环节要着重关注两类起点,一是知识起点,一是方法起点.本文中题(1)与题(2)就是提供了方法起点,通过探究,强化了问题解决的方法.尤其是题(2),通过“说明理由”,让方法更加明晰,更加有方向.这是继续探究必不可少的出发点.“问题探究”说白了,就是要找到“问题解决”所需要的“起点”.
(四)要“撑”起一定的高度
有了起点,就要让自己上升到一定的高度.从“问题探究”到“问题解决”,往往变化比较大,“横竿”设置得比较高,那么,能不能发现“变化”,能不能让自己的思维“撑”到超越“横竿”的高度,是影响问题解决的一大因素.其实,无论怎样变化,都会有“起点”的影子,“探究”中用到的方法或知识,都将会在问题解决中发挥作用.所以,在探究类问题的解题教学中,需要让学生看到怎样做才能被“撑”起高度,怎样分析才能发现“变化”,从而掌握解决此类问题的一般方法.endprint

