锅炉管弯头曲面对涡流探头阻抗的影响

李海超,徐志远,林章鹏,廖亚华

(湘潭大学 机械工程学院, 湘潭 411105)



锅炉管弯头曲面对涡流探头阻抗的影响

李海超,徐志远,林章鹏,廖亚华

(湘潭大学 机械工程学院, 湘潭 411105)

对锅炉管弯头进行涡流检测时,弯头复杂的曲面结构会对检测结果的准确性产生影响，故分析弯头曲面对探头阻抗的影响具有重要意义。通过建立放置式涡流探头检测不锈钢弯头的ANSYS有限元模型，分析了弯头弯曲半径及周向检测位置的变化对探头反射阻抗的影响，并进行了试验验证。结果表明：弯曲半径增大时，反射阻抗幅值的变化量增大，相位则减小；探头从弯头内侧往外侧移动时，反射阻抗幅值的变化量逐渐减小，而相位则增大。

涡流检测；锅炉管；弯头；阻抗；有限元法

随着高参数大容量超(超)临界机组的发展，作为关键承压部件的锅炉管的制造广泛采用了具有高热强度和高蠕变强度的奥氏体不锈钢。在长期的高温高压环境下，弯头位置易产生横向晶界腐蚀裂纹而发生爆管。另外，某些锅炉管弯头在制造过程中处理不到位，不能形成性能较好的单相奥氏体组织，短时间运行后易产生表面横向应力腐蚀裂纹[1-2]。因此，为保障机组安全运行，有必要对弯头进行定期的无损检测。近年来，涡流检测因具有非接触、速度快、精度高等优点，开始应用于锅炉管弯头的无损检测中[3-4]。

管道涡流检测分为管内检测和管外检测两种方式。锅炉管直径较小，且管内经常存在堆积物，因此不适宜采用管内检测方式。管外检测主要有外穿过式和放置式两种形式。对于连续敷设的锅炉管排，采用放置式探头检测是有效且方便的手段。锅炉管弯头具有复杂的曲面结构，导致探头到曲面的距离(提离距离)难以保持一致，从而干扰检测信号。如何抑制提离效应对检测结果的影响是曲面涡流检测面临的一个问题，国内外学者从信号处理和探头设计方面进行了研究。Takagi[5]采用近似方法将蒸汽管道简化为平板进行求解，但当管道半径相对线圈半径不够大时，这样的简化会带来很大的误差。张玉华等[6]分析了直管内外壁的凹面和凸面的弯曲半径大小及提离变化对线圈反射阻抗的影响，并提出利用相位旋转和信号增强相结合的方法消除提离干扰。宋林等[7]通过将红外成像与脉冲涡流检测相结合，应用数值仿真方法，研究了曲面零件裂纹缺陷的脉冲涡流热特性。针对具有复杂曲面的被测对象，学者们提出采用柔性探头进行检测，柔性探头能够与复杂曲面紧密贴合或者保持相对位置稳定，有效地抑制了不稳定提离[8-10]。但是，柔性探头线圈的电感量小而导致检测信号微弱，且制作的成本较高，因此，圆柱线圈仍是当下涡流检测的主要探头形式。总的说来，目前对于曲面涡流检测，圆柱线圈探头提离抑制的研究主要是针对平面或简单弧面，而柔性线圈虽可解决复杂曲面的提离问题，但实际应用较少。

锅炉管弯头是由径向弯曲及轴向弯曲形成的复杂曲面，不同位置处的曲率半径不同而引起涡流探头平均提离的变化，从而影响探头的阻抗输出。笔者基于有限元法，建立了不锈钢弯头涡流检测的三维仿真模型，分析了弯头弯曲半径的变化以及不同的检测位置对线圈探头阻抗的影响，揭示了弯头曲面变化时探头阻抗的变化规律，对抑制探头提离变化的干扰及提高检测结果的准确性提供指导意义。

1　弯头涡流检测仿真模型

图1　弯头涡流检测仿真模型

1.1模型建立

在有限元软件ANSYS中建立如图1所示的弯头涡流检测仿真模型(隐去空气)。由于弯头不关于线圈轴线旋转对称，故无法简化为二维轴对称模型，而只能建立三维模型进行分析。采用基于节点法的3D磁场分析单元SOLID97给弯头、探头和空气建立模型。不锈钢管道外径18 mm，内径8 mm，壁厚5 mm，相对磁导率μr=1，电导率σ=3.82×107S·m-1。考虑到实际管线以水平和竖直走向为主，因此，弯头角度取90°。弯曲部位的弯曲半径设置为40～65 mm。探头线圈外径7.5 mm，内径4.5 mm，高3 mm，匝数200，相对磁导率μr=1，线圈置于弯头中部，其轴线垂直于管壁表面，底面中心到管壁的距离(提离距离)为0.5 mm。为保证线圈磁场的有效衰减，管道和线圈周围用10倍于线圈外径的空气域包围。

1.2网格划分

模型单元的划分是决定有限元仿真精度的一个关键因素。考虑到弯头曲面的特殊性，为在保证精度的同时节约计算机时，采用分块划分的思想，其基本原则为：① 由于电涡流的趋肤效应，趋肤深度内至少应该有两层网格，探头下方的弯头磁场变化较快，应划分较密的单元。② 管壁内磁场的变化梯度从探头下方往两端逐渐减小，采用渐变式网格，远离探头的弯头单元尺寸逐渐增大。③ 探头线圈为激励和接收元件，应划分较密单元。④ 空气域采用自由网格划分，但应控制单元所允许的最小尺寸，避免出现尖角网格。在划分单元时，通过选定模型轴向、周向及径向对应的线段并指定其划分数目来控制单元的精细程度。

1.3加载与求解

给线圈加载4 V,100 kHz的正弦交流电压，并耦合线圈所有节点电流。空气最外层边界施加磁通量平行条件，模型内介质交界面上的边界条件为自然边界条件，在计算中自动满足。选择分析类型为谐波分析，对不同的检测情况分别进行参数化建模和求解。使用Get命令提取线圈中任意节点的电流值，通过计算线圈电压与电流之比得到线圈阻抗，并进一步算出阻抗的相对变化量<φ;其中，ΔZ=Z-Zair，Z为线圈置于弯头上方时的阻抗，Zair为线圈置于空气中的阻抗,φ为相位。

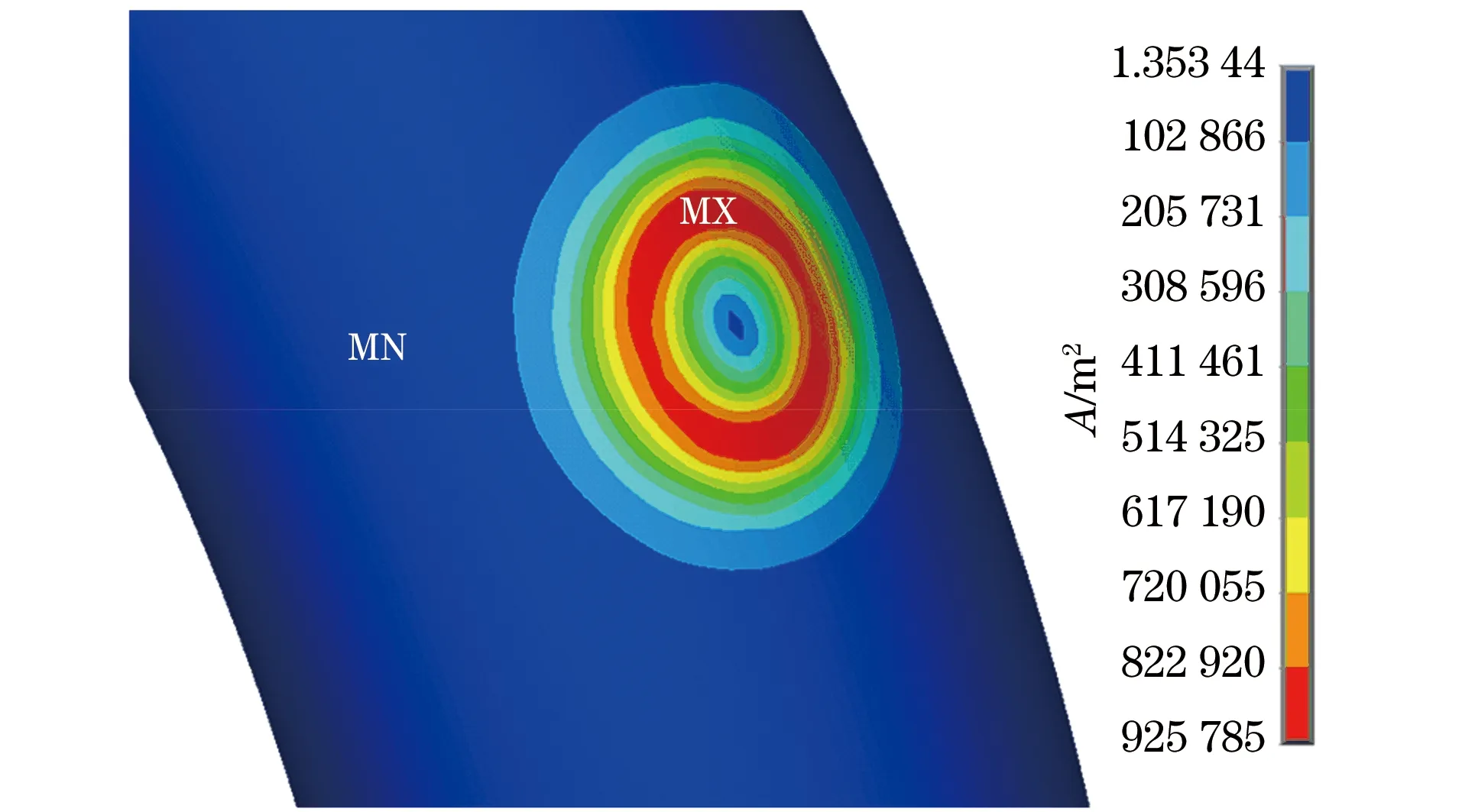
图2　弯头上方电涡流密度图

2　仿真结果分析

图2为探头线圈正对弯头中部外侧时管壁中的感应涡流分布。从图中可看出，电涡流在管壁表面呈空间同心椭圆分布，这是由于弯头曲面形状的变化使得线圈到管壁不同位置的提离距离不一致，导致线圈磁场与管壁的耦合强度不同。因此，管壁轴向的感应涡流总体上比周向的感应涡流强，涡流最大值(图中以MX标记)出现在管壁的轴向。

保持探头线圈的位置不变，分别在弯头弯曲半径r为40,45,50,55,60,65 mm处进行仿真试验，得到探头线圈中电流实部和虚部的变化如图3所示。可以看出，随着弯曲半径的增大，电流实部Ireal和虚部Iimag的幅值均逐渐增大，但实部的增加速度更快。

图3　弯曲半径r的变化对线圈电流的影响

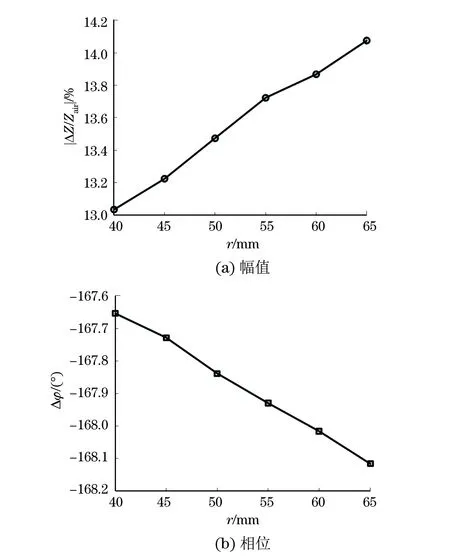
图4　弯曲半径r的变化对线圈反射阻抗ΔZ的影响

弯曲半径r对探头线圈反射阻抗ΔZ的影响如图4所示，可以看出：随着r从40 mm增加到 65 mm，阻抗的幅值变化由13.04%增加到14.08%，相位Δφ的变化由-167.65°减小到-168.12°，仅改变0.47°。这说明弯曲半径的变化对反射阻抗的影响主要体现在阻抗幅值上，对相位的影响较小。由于弯头弯曲半径r的变化，线圈到管壁表面的平均提离随之改变，r越大，则平均提离越小，管壁中感应的电涡流越强，阻抗变化越明显。

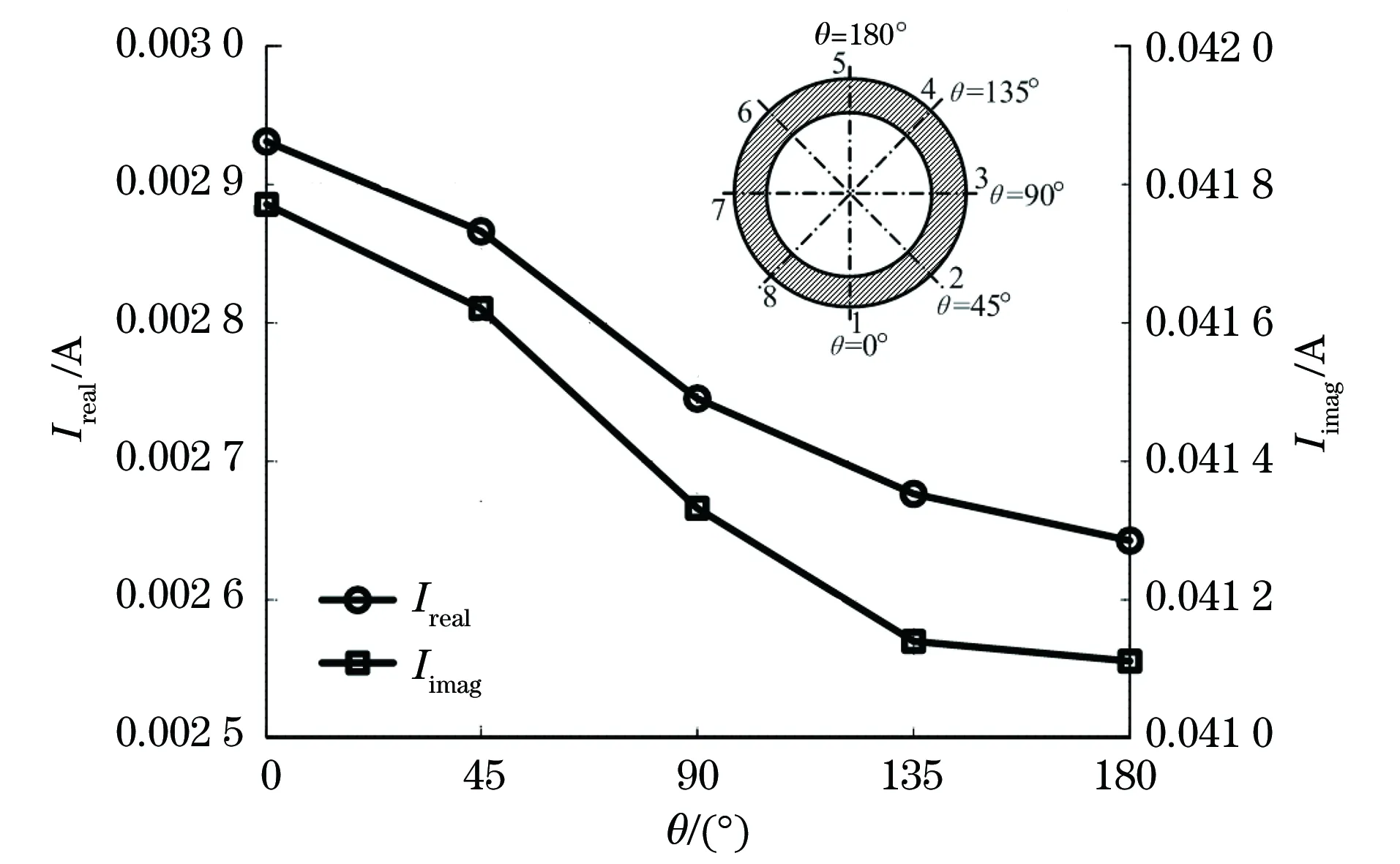
图5　检测位置θ的变化对线圈电流的影响

保持弯头的弯曲半径r为40 mm不变，按照国家标准GB/T 28075-2012 《无损检测 脉冲涡流检测方法》划分管道的周向检测区域(图5)，其中区域6、7、8分别和区域4、3、2对称，因此只考虑区域1～5的情况。依次改变探头的周向位置θ进行仿真试验，分别得到如图5,6所示的探头线圈电流I及反射阻抗ΔZ的变化规律。从图中可以发现，探头从区域1移动到5时，电流实部Ireal、虚部Iimag大小均减小；线圈反射阻抗幅值变化量逐渐减小，在弯头内侧的区域1变化最大(为15.02%)，而在弯头外侧的区域5变化最小(为13.06%)；相位角则逐渐增大，但变化量很小。造成上述现象的原因是：在弯头弯曲半径不变的条件下，虽然管道的周向弯曲程度相同，但由于弯头还存在轴向弯曲，不同θ处的曲面是连续变化的；在弯头正下方的区域1，探头线圈的平均提离最小，往上变化检测位置，平均提离逐渐增大，所以，管壁中感应涡流的强度从区域1往5递减，对应的线圈反射阻抗变化越来越小。

图6　检测位置θ的变化对线圈反射阻抗ΔZ的影响

设R、ωL分别为线圈检测弯头时的电阻和电抗，Rair、ωLair分别为探头线圈处于空气中的电阻和电抗，则弯头弯曲半径和检测位置改变所形成的阻抗平面分别如图7,8所示。由于导体内热能损耗和磁能存储的缘故，线圈的电阻R增大而电抗ωL减小。弯头弯曲半径r增大使得两者的变化量均增大，符合图4中ΔZ的变化规律；而检测位置θ由下而上变化则使得两者的变化量均减小，符合图6中ΔZ的变化规律。本质上，这两个因素变化对阻抗的影响都是由于改变了探头线圈到管壁的平均提离，从而使得线圈与管壁的电磁耦合强度发生变化。

图7　弯曲半径r变化时的线圈阻抗图

图8　检测位置θ变化时的线圈阻抗图

由以上的分析可知，管道弯头处弯曲半径和周向检测位置的变化均会引起探头阻抗的改变。而目前在管道涡流检测中，通常以直管段未腐蚀区域的检测结果为参考来评估整条管线的腐蚀情况，这势必会对弯头的检测结果带来一定的误差。因此，实际检测中应当按上述规律对弯头的探头阻抗值进行补偿或修正，以保证弯头检测结果的准确性。

3　试验验证

搭建如图9所示的涡流检测平台对弯头试件进行了检测。试件规格为φ57 mm×5 mm，弯头角度90°，材料为304不锈钢。涡流传感器的型号为MTM-1808，该传感器内部在输入端集成了逆变电路，在输出端集成了阻抗/电压变换、检波及滤波电路。因此，传感器输入和输出都为直流电压。传感器位于空气中的输出电压U为10 V；置于试件上时由于涡流场感生电压的削弱作用，输出电压小于10 V。反射阻抗ΔZ越大，则削弱作用越强，输出电压越小。制作了一个塑料保持架以保证传感器在不同周向位置的提离距离为0.5 mm不变。给传感器输入15 V直流电压，使用万用表测量传感器置于弯头不同周向位置时的输出电压值，其结果如图10所示。可看出，传感器从弯头内侧往外侧移动时，输出电压的幅值逐渐增大，间接反映了反射阻抗逐渐减小的规律，这与图6(a)所示的阻抗的变化规律一致，从而验证了上文仿真结论的正确性。

图9　涡流检测平台外观

图10　传感器输出电压随检测位置的变化 4　结论

通过建立放置式涡流探头检测不锈钢管道弯头的有限元模型，分析了弯头处弯曲半径及周向检测位置的变化对探头反射阻抗的影响，并进行了试验验证，得出以下结论：弯曲半径增大时，反射阻抗幅值的变化量增大，相位则减小；探头从弯头内侧往外侧移动时，反射阻抗幅值的变化量逐渐减小，而相位则增大。这两种现象都是由于探头到管壁的平均提离发生了改变而引起的。试验结果对提高锅炉管弯头涡流检测结果的准确性具有一定的指导意义。后续进一步的工作将探讨对弯头涡流检测结果的补偿方法及探头倾斜的影响等内容。

[1]张国华, 李敬高. 奥氏体不锈钢应力腐蚀分析研究[J]. 焊接技术,2002, 31(6): 53-54.

[2]李萌, 胡斌. 奥氏体不锈钢中马氏体含量的相关无损检测方法[J]. 无损检测, 2014, 36(7): 19-24,66.

[3]沈丁杰, 邹建伟, 胡彬. 锅炉受热面奥氏体不锈钢管弯头表面裂纹涡流检测技术研究[J]. 湖南电力,2011, 31(3):5-7.

[4]刘金秋.奥氏体锅炉管内壁氧化皮脱落堆积测量技术研究[D]. 济南: 山东大学, 2011.

[5]TAKAGI T. Benchmark models of eddy current testing for steam generator tube: experiment and numerical analysis[J]. International Journal of Applied Electromagnetics in Materials, 1994, 5(3): 149-162.[6]张玉华, 孙慧贤, 罗飞路. 小曲率半径弧面涡流检测中探头提离干扰的抑制方法[J]. 中国电机工程学报, 2009, 29(27): 126-132.

[7]宋林, 杨随先, 李小建, 等. 曲面零件裂纹缺陷脉冲涡流热成像检测的仿真[J]. 无损检测, 2012, 34(9): 39-41.

[8]GILLES-PASCAUD C, DECITRE J M, VACHER F, et al. Eddy current flexible probes for complex geometries[J]. Review of Progress in Quantitative Nondestructive Evaluation, 2005, 25: 399-406.

[9]SHEIRETOV Y, GRUNDY D, ZILBERSTEIN V, et al. MWM-array sensors for in situ monitoring of high-temperature components in power plants[J]. Sensors Journal, IEEE, 2009, 9(11): 1527-1536.

[10]丁天怀, 陈祥林. 用于测量曲面间隙的电涡流传感器线圈[J]. 清华大学学报: 自然科学版, 2006, 46(2): 180-183.

[11]GB/T 28075-2012无损检测 脉冲涡流检测方法[S].

The Influence of the Elbow Surface of Boiler Tube on Eddy Current Probe′s Impedance

LI Hai-chao，XU Zhi-yuan，LIN Zhang-peng，LIAO Ya-hua

(School of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China)

The complex structure of elbow surface is the main difficulty which hampers eddy current technique being conducted on boiler tube elbow. Therefore, in order to improve the detection accuracy, it is of great significance to study the influence of the elbow surface on probe’s impedance. In this paper, the finite element model of a pancake probe-coil over a stainless steel tube elbow was established. Influences of the variations of the pipe’s curvature radius and the probe′s circumferential detecting position on the probe’s reflected impedance were respectively studied. Also, an experiment validation of the simulation was conducted. The results are as follows: (i) as the radius of curvature increases, the variation of the reflected impedance amplitude increases but the impedance phase decreases. (ii) as the probe is moved from the inner side of the elbow to the outer side, the variation of the reflected impedance amplitude decreases but the impedance phase increases.

Eddy current testing; Boiler tube; Elbow; Impedance; Finite element method

2015-03-19

国家自然科学基金资助项目(51505406);湖南省教育厅资助科研项目(15C1323)

李海超(1989-),男,硕士研究生,主要从事电涡流无损检测技术的研究。

10.11973/wsjc201510013

TG115.28

A

1000-6656(2015)10-0056-04