基于实时反馈的机床热误差在线补偿模型

张成新　高　峰　李　艳

西安理工大学，西安，710048

基于实时反馈的机床热误差在线补偿模型

张成新高峰李艳

西安理工大学，西安，710048

为建立一种能够适应机床不同工况且具有准确预测能力的热误差补偿模型，提出一种基于限定记忆递推最小二乘法辨识热误差模型参数的机床热误差预测建模方法。该方法随着机床工作状况的改变，根据实时反馈的温度和热误差数据，采用递推方法对模型参数进行即时修正，使热误差模型能够及时跟踪机床系统的热特性变化，实现以较高的预测精度对机床热误差进行补偿。通过数控车床主轴轴向热误差辨识建模及补偿实验可以看出，限定记忆递推最小二乘法比一步最小二乘法辨识精度有较大提高，最大残差值减小了52.3%，标准差减小了67%。实验结果表明，利用该方法进行机床热误差模型参数辨识具有较高的预测精度和鲁棒性，有效可行。

数控机床；热误差；在线补偿；限定记忆递推最小二乘法

0　引言

精密机械加工中，机床热误差是造成零件加工误差的最主要因素，为了减小或消除热误差对机床加工精度的影响，研究人员进行了广泛深入的研究并提出了各种解决方案[1-3]，主要有硬件防止法和软件补偿法，软件补偿法是通过实验方法建立热误差补偿模型，由于其应用成本低且无需对机床进行改造，所以是目前的研究热点。但是机床热误差受加工条件、周围环境等因素的影响，很难建立一种完全能够适应不同环境和加工状态变化的误差补偿模型。文献[4-6]建模时根据采集到的温度和热误差数据分别利用灰色模型、最小二乘支持向量机和多元线性回归模型对机床热误差进行一次性建模，但由于机床热误差是一时变系统，根据固定数据建立的模型适应性较差。为了提高模型的预测精度和鲁棒性，有些学者提出了实时在线建模方法。文献[7]根据环境和加工状态变化，采用递推最小二乘实时辨识多项式参数来提高模型的适应能力和预测精度。文献[8]采用动态自适应模型，依据实时反馈热误差不断修正模型参数，使该模型具有较高的预测精度和鲁棒性，能够适应多种加工环境变化。文献[9]通过在线最小二乘支持向量机建立了机床热误差实时补偿模型，在加工过程中根据不断输入的新数据修正模型参数，使补偿模型具有较高的补偿精度和鲁棒性。文献[10]利用贝叶斯网络推理建立机床热误差模型，根据温度和热误差反馈信息在线修正模型参数，具有较好的适应能力。

以上几种在线建模方法根据反馈数据进行实时建模时，老数据的作用一直存在，随着采样数据的增加会造成“数据饱和”现象使建模结果不稳定[12]，而限定记忆递推最小二乘法能够突出当前数据的作用，丢弃过老数据，始终采用最近有限长度的采样数据序列，使补偿模型能够适应当前机床加工状态或环境温度的变化，提高模型的预测精度和鲁棒性。为此，本文提出基于限定记忆递推最小二乘实时辨识差分方程模型参数的机床热误差在线建模方法，实时跟踪机床热环境和热误差的变化，并始终保持模型良好的预测精度。通过数控车床主轴轴向热误差补偿实验进行验证，并用实验表明该方法的可行性。

1　机床热误差模型

机床热误差模型一般多采用多项式回归模型或神经网络建模，但是由于材料热弹性变形的伪滞后特性[11]，致使上述模型不能全面揭示机床的热变形过程而造成补偿效果不好，多项式回归模型的输出只跟当前时刻的输入值有关。为了克服热变形的伪滞后特性提高模型预测精度，本文采用差分方程模型描述热膨胀物理过程，模型当前热位移输出不仅与当前温度输入有关，还和前时刻的温度输入数据有关，所以差分模型更能准确反映机床的热误差变化过程。

一般n阶差分方程形式为

E(k)+a1E(k-1)+…+anE(k-n)=

b0T(k)+b1T(k-1)+…+bnT(k-n)

(1)

式中，k为采样时刻；ai、bi(i=1,2,…,n)为方程系数；E(k)、T(k)分别为系统的输出和输入序列。

引入单位延迟算子z-1，其定义为

z-1E(k)=E(k-1)

(2)

以及系数多项式：

(3)

由式(2)和式(3)，式(1)可以表示为

A(z-1)E(k)=B(z-1)T(k)

(4)

E(k)=θT(k)

(5)

机床热误差模型一般有多个温度输入变量，多个位移输出量，是一个多输入多输出系统，如图1所示。

图1　机床热误差系统示意图

对于多输入多输出系统辨识相对比较复杂，为了便于辨识，将机床各个方向的热误差模型单独表示，例如三坐标铣床热误差系统可以表示为n输入3输出的系统，按照式(4)的结构，可表示为

(6)

T(k)=[T1(k)T2(k)…Tn(k)]T

2　限定记忆最小二乘递推算法

式(6)中各个方向的系数多项式可以采用最小二乘进行估计一次性算出，但其无法反映系统的时变特性，模型适应能力较差。为了使模型能够跟踪加工环境和机床热特性的变化，必须采用递推算法建模。但一般递推最小二乘算法属于增长记忆算法，随着采集数据的增加，递推算法从新数据中获得的新信息相对下降使算法慢慢失去修正作用，造成“数据饱和”。限定记忆最小二乘递推算法是每次迭代时只依赖于最新的有限固定长度数据序列，即得到一个新数据，就去掉一个老数据，从而消除了老数据的影响，有效克服“数据饱和”现象，防止估计发散。针对式(1)形式，其限定记忆最小二乘法的递推公式[12]如下：

(7)

(8)

限定记忆的递推算法流程如下：

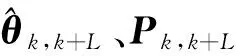
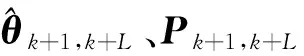
随着采样数据的进入，根据步骤(2)和步骤(3)不断循环递推，就可实时更新模型参数。

3　实验及结果分析

图2　车床测量传感器布置

(a)主轴测点温度变化曲线

(b)主轴轴向热误差曲线图3　车床主轴温度和热误差曲线

本研究在数控车床上对主轴轴向热误差进行建模实验。车床主轴部分的热误差主要由轴承部分转动发热造成，所以在主轴头部轴承圈部位放置3个温度传感器用来检测主轴轴承的温度变化，芯棒端部安装1个电涡流位移传感器用来检测主轴轴向的热伸长量，如图2所示。测试时主轴及环境温度如下：室温20 ℃，主轴初始温度和室温相同；主轴以1000r/min运转160min，然后停机冷却。机床运行过程中温度和位移传感器每隔5min采样一次，滤除粗大误差后主轴温度测点温度变化量和位移变化量曲线分别如图3a、图3b所示。

3.1温度测点和热误差模型结构的确定

测试结果表明3个温度传感器变化趋势相同，通过Fisher最优分割法[13]判定，选择T1温度传感器的温度作为输入温度变量，因此车床主轴热膨胀系统可以简化为单输入单输出系统，如式(1)所示形式。根据文献[8]一般机床热系统可以近似为如下二阶差分方程：

E(k)=-a1E(k-1)-a2E(k-2)+

b0T(k-1)+b1T(k-2)

(9)

3.2建模结果分析

图4　最小二乘辨识预测效果图

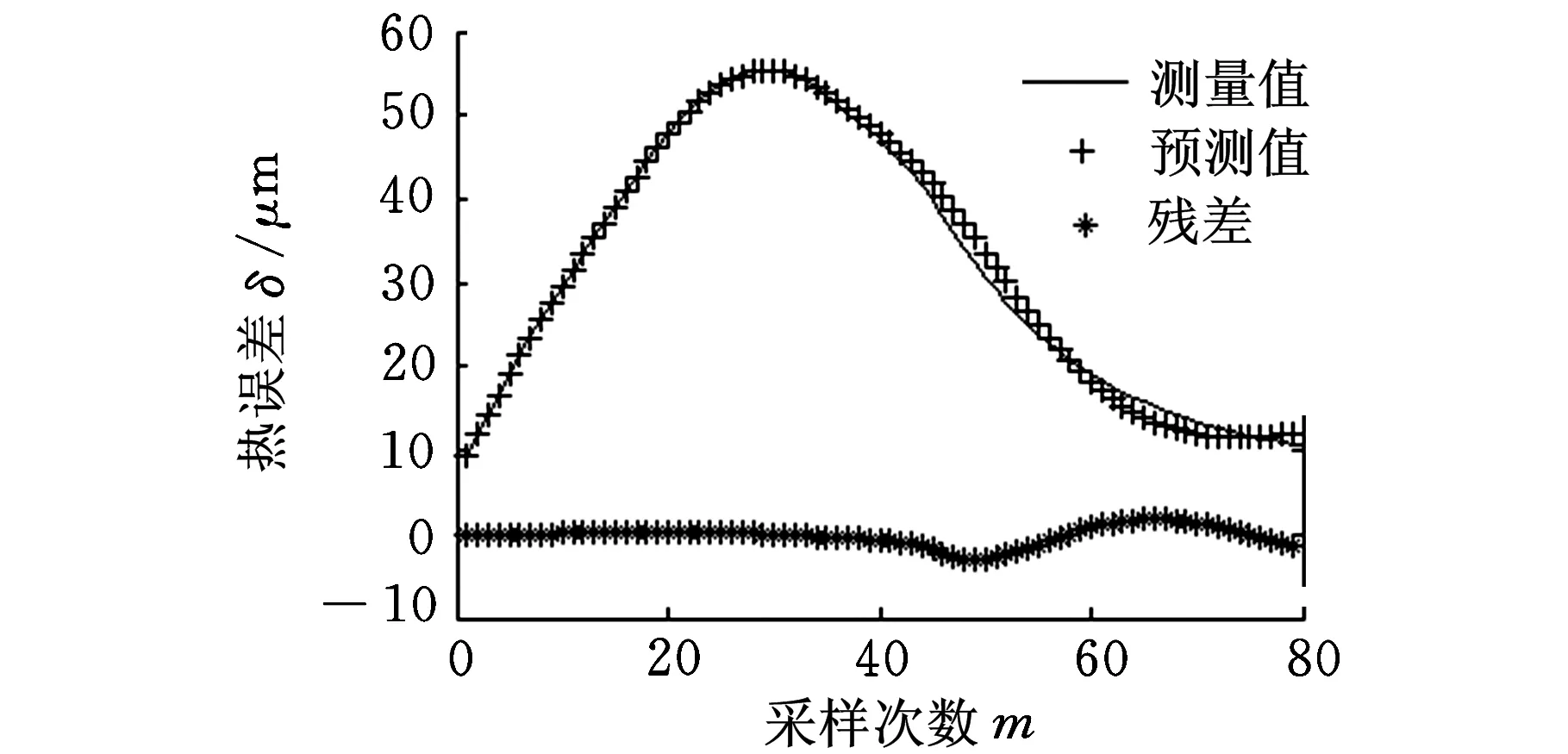
图5　限定记忆最小二乘法辨识效果图

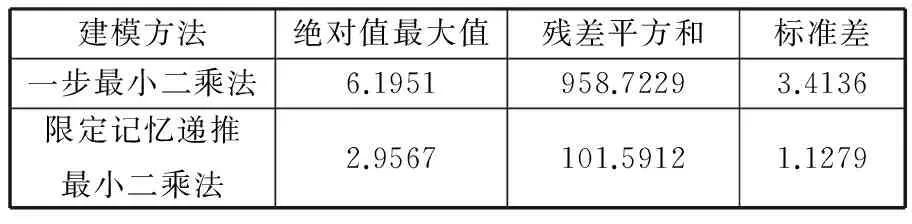
表1　模型残差指标比较　μm

从图4和图5可以看出，限定记忆递推最小二乘模型比一步最小二乘模型的建模效果要好得多。对于一步最小二乘模型，从图4可以看到，在第18次采样时残差波动逐渐增大，到第52次采样时达到最大6.1951μm。说明随着工作状态的变化，误差模型参数偏离实际较大，固定参数模型不能对时变系统热误差进行较好的预测而出现较大波动。图5中基于限定记忆递推方法模型显示，由于升温阶段温度变化相对平稳，模型在升温阶段预测效果相当准确；在降温时由于系统状态发生变化，在第50次采样附近产生了一次波动，随后模型立即调整参数跟踪机床状态，从而使热误差预测值和测量值不至于相差过大，总体热误差预测效果较好。限定记忆递推最小二乘法由于对参数进行辨识时只依赖于最新的一段固定长度数据，而过老的数据被剔除，这样所建模型就能够反映出系统的最新状态变化，自适应能力好，所以预测精度较高。

4　结论

本文为了提高机床热误差补偿模型的精度和鲁棒性，采用限定记忆递推最小二乘辨识建立热误差补偿模型。该方法根据实时反馈的温度和热误差数据，采用固定长度的采样数据不断递推更新模型，适用于时变参数系统的实时在线补偿预测。由于采用固定长度数据进行递推运算，消除了老数据对模型的影响，使模型能够跟踪机床系统的热误差变化，从而提高了补偿模型的适应能力。实验结果表明：采用限定记忆递推最小二乘模型比一步最小二乘模型预测残差最大值减小了52.3%，残差标准差减小了67%，说明限定记忆递推最小二乘模型预测精度较高，该建模方法能够满足机床热误差建模补偿的精度和鲁棒性要求。

[1]MayrJ,JedrzejewskiJ,UhlmannE,etal.ThermalIssuesinMachineTools[J].CIRPAnnals-ManufacturingTechnology, 2012, 61(2): 771-791.

[2]VyroubalJ.CompensationofMachineToolThermalDeformationinSpindleAxisDirectionBasedonDecompositionMethod[J].PrecisionEngineering, 2012, 36(1): 121-127.

[3]MarseM,HorejsO,HornychJ,etal.RobustnessandPortabilityofMachineToolThermalErrorCompensationModelBasedonControlofParticipationThermalSources[J].JournalofMachineEngineering, 2013, 13(1)

[4]闫嘉钰,杨建国. 灰色GM(X, N)模型在数控机床热误差建模中的应用[J]. 中国机械工程, 2009, 20(11): 1297-1300.

YanJiayu,YangJianguo.ApplicationofGreyGM(X,N)ModelonCNCMachineThermalErrorModeling[J].ChinaMechanicalEngineering, 2009, 20(11): 1297-1300.

[5]林伟青,傅建中,许亚洲,等. 基于LS-SVM与遗传算法的数控机床热误差辨识温度传感器优化策略[J]. 光学精密工程, 2008, 16(9):1684-1687.

LinWeiqing,FuJianzhong,XuYazhou,etal.OptimalSensorPlacementforThermalErrorIdentificationofNCMachineToolBasedonLS—SVMandGeneticAlgorithm[J].OpticsandPrecisionEngineering, 2008, 16(9):1684-1687.

[6]凡志磊,李中华,杨建国. 基于偏相关分析的数控机床温度布点优化及其热误差建模[J]. 中国机械工程, 2010, 21(17): 2025-2028.

FanZhilei,LiZhonghua,YangJianguo.NCMachineToolTemperatureMeasuringPointOptimizationandThermalErrorModelingBasedonPartialCorrelationAnalysis[J].ChinaMechanicalEngineering, 2010, 21(17): 2025-2028.

[7]杨建国,任永强,朱卫斌. 数控机床热误差补偿模型在线修正方法研究[J]. 机械工程学报, 2003, 39(3): 81-84.

YangJianguo,RenYongqiang,ZhuWeibin.ResearchOn-lineModelingMethodofThermalErorCompensationModelforCNCMachines[J].ChineseJournalofMechanicalEngineering，2003, 39(3): 81-84.

[8]YangH,NiJ.AdaptiveModelEstimationofMachine-toolThermalErrorsBasedonRecursiveDynamicModelingStrategy[J].InternationalJournalofMachineToolsandManufacture, 2005, 45(1): 1-11.

[9]林伟青,傅建中,许亚洲,等. 基于在线最小二乘支持向量机的数控机床热误差建模与补偿[J]. 计算机集成制造系统, 2008, 14(2):295-299.

LinWeiqing,FuJianzhong,XuYazhou,etal.ThermalErrorModeling&CompensationofNumericalControlMachineToolsBasedonOn-lineLeastSquaresSupportVectorMachine[J].ComputerIntegratedManufacturingSystems, 2008, 14(2): 295-299.

[10]吴雄彪,姚鑫骅,傅建中. 基于贝叶斯网络的数控机床热误差建模[J]. 中国机械工程, 2009, 20(3): 293-296.

WuXiongbiao,YaoXinhua,FuJianzhong.ThermalErrorModelingofNCMachineToolsBasedonBayesianNetworks[J].ChinaMechanicalEngineering, 2009, 20(3): 293-296.

[11]YangH,NiJ.DynamicModelingforMachineToolThermalErrorCompensation[J].Transactions-AmericanSocityofMechanicalEngineeringJournalofManufacturingScienceandEngineering, 2003, 125(2): 245-254.

[12]刘党辉, 蔡远文, 苏永芝, 等. 系统辨识方法及应用[M]. 北京：国防工业出版社,2010.

[13]高峰, 刘江, 杨新刚, 等. 基于Fisher最优分割法的机床热关键点优化研究[J]. 仪器仪表学报, 2013, 34(5): 1070-1075.

GaoFei,LiuJian,YangXingan.StudyonOptimizationTthermalKeypointsforMachineToolsBasedonFisherOptimalSegmentationMethod[J].ChineseJournalofScientificInstrument, 2013, 34(5): 1070-1075.

(编辑郭伟)

On-line Compensation Model Based on Real-time Feedback Thermal Errors of Machine Tools

Zhang ChengxinGao FengLi Yan

Xi’an University of Technology,Xi’an,710048

In order to compensate the thermal errors with accurate prediction under various working conditions of machine tools, a novel thermal error prediction modeling method with RFMLS method was presented. As variations in working condition of machine tools, according to real-time online feedback data of temperature and thermal deformation of key measuring points, thermal error model could trace the thermal characteristics by using recursive algorithm to update the model’s parameters timely, so the thermal compensation would be carried out successfully. The method was verified by an axial thermal error compensation experiment of spindle conducted on a CNC lathe. The experimental results show that predictive model with RFMLS is more accurate than that with least squares method, the maximum residual error and standard deviation of the former decrease by 52.3% and 67% than those of the latter respectively. Hence the thermal error of machine tools compensated by the presented method can improve accuracy and reduce the model predictive errors effectively.

CNC machine tool；thermal error；on-line compensation；finite memory recursive least squares(RFMLS)

2013-11-12

国家自然科学基金资助项目(51375382);国家科技重大专项(2012ZX04012032);陕西省自然科学基础研究计划重点项目(S2009JC1400)

TH161< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.03.013

张成新，男，1975年生。西安理工大学机械及精密仪器工程学院博士研究生。主要研究方向为机床热误差补偿。高峰，男，1969年生。西安理工大学机械及精密仪器工程学院教授、博士研究生导师。