Job Shop调度问题的Minimax模型及双空间协同遗传算法
杨宏安 席志成 夏常凯 王经国
西北工业大学现代设计与集成制造教育部重点实验室,西安,710072
Job Shop调度问题的Minimax模型及双空间协同遗传算法
杨宏安席志成夏常凯王经国
西北工业大学现代设计与集成制造教育部重点实验室,西安,710072
针对工序加工时间不确定环境下的Job Shop调度问题,为了预估最差调度工况及其对应的调度性能指标边界,采用一类保守、稳健的Minimax分析方法,建立了基于提前/拖期惩罚成本的Minimax调度模型;为了解决传统基于遍历或枚举方法存在的搜索空间巨大的问题,提出并证明了给定调度顺序条件下,关于内层Max优化过程的凸函数定理,并依此定理提出了一种工序加工时间搜索空间过滤机制。针对Minimax调度问题存在的双空间寻优特性,在分析调度顺序种群和工序加工时间种群的交替进化机制的基础上,设计了一种高效的双空间协同遗传算法。最后通过仿真算例验证了该过滤机制和双空间协同遗传算法的有效性。
作业车间调度;工序加工时间不确定;提前/拖期;Minimax;双空间协同进化
0 引言
传统作业车间调度问题(job shop scheduling problem,JSSP)基本上都是假设调度参数已知且忽略各种扰动因素。然而,从辩证的观点看:在人、机、料、法、环组成的复杂制造系统中,不确定性是绝对的,而确定性则是相对的[1]。车间内部的机器故障、刀具损坏、人员缺勤、质量问题,以及车间外部的订单调整、交货期变更诸多因素,使得车间调度具有不确定性、随机性和复杂性等显著特征,从而导致确定性调度优化方案在不确定性扰动冲击下其性能指标急剧劣化[2]。由于操作工人技能差异、刀具磨损、特种工艺、质量检验等诸多因素,使得工件的部分关键工序,甚至所有工序的加工时间呈现显著的不确定特征。因此,工序加工时间是JSSP中最普遍、最有代表性的一类不确定性因素。本文将研究对象聚焦于工序加工时间不确定环境下的作业车间调度问题(job shop scheduling problem with processing time variability,JSSP-PTV)。
目前,求解JSSP-PTV问题的方法分三类[3],即随机规划方法、模糊规划方法、区间数方法,相应的对工序加工时间不确定变量的描述方式分为概率分布函数描述、模糊数描述、区间数描述。然而随机规划方法和模糊数方法都要求知道随机变量的准确概率分布,实际中由于不确定扰动因素众多、复杂,根本无法得到工序加工时间不确定变量的准确概率分布,但可以根据大量试验数据比较容易地确定其变化范围,因此本文以区间数这类非概率方式描述工序加工时间不确定变量。针对工序加工时间的大幅度扰动,Minimax方法是以最小化调度方案在工序加工时间所有可能取值条件下的最差性能作为调度目标,这类保守、可靠的主动调度方法可以事先预估最差情景及其对应的调度性能指标,保证调度的鲁棒性,且能够有效控制决策风险。
工序加工时间不确定因素使得调度搜索空间急剧增大。因此,如何有效缩减搜索空间是求解该类不确定调度问题的重要内容。文献[4]在单机调度问题研究中建立了基于以Flow time偏差为调度指标的Minimax模型,提出并证明了给定调度顺序条件下,该目标函数在工序加工时间取其值域上界值或下界值时取得最大值;文献[5]针对单机调度环境下的一类提前/拖期调度指标,提出并证明了一种有效预过滤搜索空间的凸函数定理。针对并行机调度问题,文献[6]建立了以makespan绝对偏差为调度指标的Minimax模型,提出并证明了与文献[4]和文献[5]类似的定理和结论。
由于Minimax问题中存在两个寻优空间,因此在调度算法设计时一般采用内外层嵌套或协同方法进行双空间优化求解。针对经典的Minimax优化问题,文献[7-8]提出了一种较为通用的双空间协同遗传算法,文献[9]分析了Minimax问题的双优化方向、欺骗性、内层Max寻优精度对整个算法性能影响较大等特征,并针对常规迭代法求解Minimax问题的缺陷,对算法提出了一种改进措施。针对Minimax调度问题的双空间优化,文献[5]针对单机调度问题采用双层嵌套遗传算法进行求解,文献[10]采用最为保守的绝对鲁棒调度策略,建立了以makespan为调度指标Minimax调度模型,并通过双空间协同算法优化求解。
现有研究基本都是基于正规调度指标的Minimax问题,或是简单的单机调度问题,而文献[5]所采用的双空间嵌套遗传算法虽然结构层次清晰易懂,直观地反应了内外空间的嵌套关系,但是这类传统优化求解机制由于效率低下,只适用于小规模的调度问题。本文则在文献[5]的基础上,提出并证明了凸函数定理也适用于JSSP-PTV这类复杂的多机调度问题;针对Minimax调度问题的双空间优化特性,分析并提出了一种调度顺序种群和工序加工时间种群的交替进化机制,并依此为基础,形成了一个完整的求解Minimax调度模型的双空间协同遗传算法(two space co-evolutionary genetic algorithm,TSC-GA),以期在工序加工时间有较大波动范围的调度环境下,为调度决策者提供一种可靠、稳健的调度指标性能界。
1 Job Shop调度的Minimax模型及其特征分析
1.1Minimax调度模型


表1 Minimax调度模型的符号说明
JSSP-PTV问题的Minimax调度模型如下:
(1)
s.t.
fi(Ci(x,s))=eiEi+tiTi
(2)
Ei=max(0,di-Ci(x,s))i=1,2,…,n
(3)
Ti=max(0,Ci(x,s)-di)i=1,2,…,n
(5)
(6)
(7)
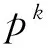
1.2工序加工时间不确定条件下的Minimax问题特征分析
Minimax调度模型包括Min优化和Max优化两个截然相反的优化过程,这使得Minimax问题与单纯的Min或者Max问题有着显著差异。
(1)双空间寻优。由式(1)可知,Minimax问题需要优化两个空间:调度顺序空间和工序加工时间空间。当调度顺序给定后,在加工时间空间内搜索对应的最差性能,这是一个最大化寻优过程;在最小化寻优过程中,搜索使最差性能最好的调度顺序。因此,双空间寻优的Minimax问题比单一空间内的传统Min或Max优化问题更为复杂。
(2)收敛过程震荡。Minimax优化过程包括最小化和最大化两个优化进程,且二者对同一个目标函数值的寻优方向相反,因此,当两个优化进程的进化速度存在差异时,对于整个调度算法而言,调度目标函数值可能会出现显著的震荡现象,从而使得整个算法的收敛速度较慢,且呈现震荡收敛趋势。
(3)内层Max寻优精度对整个调度算法影响较大。Minimax问题存在内层Max优化和外层Min优化两个寻优方向相反的过程,所以与传统Min优化问题的最大不同之处在于,其最终输出的目标函数值不是越小越好,一个看似最终目标函数值更小的结果,可能是外层调度顺序种群Min寻优彻底带来的结果,也可能是因为内层工序加工时间种群Max优化不彻底导致的欺骗性结果。可见,内层工序加工时间种群的寻优精度不仅指导本身的进化方向,还影响着外层调度顺序种群的进化方向。因此,内层工序加工时间种群的寻优精度对存在两空间优化的Minimax优化问题的整体结果影响较大。
2 内层Max优化的凸函数定理及工序加工时间可行域的过滤机制
由于JSSP-PTV问题中的工序加工时间为不确定变量,将使得整个调度搜索空间庞大。以简单的6×6 JSSP-PTV为例:假设各工序的加工时间服从均匀分布,且每道工序各有10个离散可能取值,对于任一给定的调度顺序,其对应的整个工序加工时间搜索空间规模将达到1036。因此,如何预先缩减工序加工时间的取值范围,并依此来有效过滤部分搜索空间,成为求解JSSP-PTV这类复杂不确定调度问题的首要问题之一。
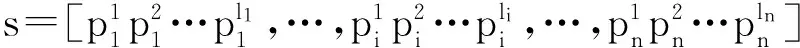
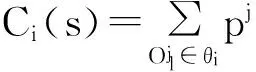
设s1、s2为工序加工时间可行域S中的任意两个不同的一维数组,且0<λ<1,由上述Ci(s)与s中各元素的非负线性组合性质得出
Ci(λ s1+(1-λ)s2)=λ Ci(s1)+(1-λ)Ci(s2)
(8)
由式(2)和式(8)得
fi(Ci(λ s1+(1-λ)s2))=fi(λ Ci(s1)+
(1-λ)Ci(s2))=max{ei(di-Ci(λ s1+(1-λ)s2)),
ti(Ci(λ s1+(1-λ)s2)-di)}
(9)
再由式(8)和式(9)推导出
λ fi(Ci(s1))+(1-λ)fi(Ci(s2))=
λmax{ei(di-Ci(s1)),ti(Ci(s1)-di)}+
(1-λ)max{ei(di-Ci(s2)),ti(Ci(s2)-di)}≥
max{λ ei(di-Ci(s1))+(1-λ)ei(di-Ci(s2)),
λ ti(Ci(s1)-di)+(1-λ)ti(Ci(s2)-di)}=
max{ei(di-Ci(λ s1+(1-λ)s2)),
ti(Ci(λ s1+(1-λ)s2)-di)}
即
λ fi(Ci(s1))+(1-λ)fi(Ci(s2))≥
fi(λ Ci(s1)+(1-λ)Ci(s2))
(10)
依据凸函数判定定理[11]和式(10)可知:fi(Ci(x,s))是s的凸函数。
根据凸函数性质[11]“有限个凸函数的非负线性组合仍然是凸函数”,则由上述关于任一工件的提前/拖期惩罚成本是s的凸函数(性质1),对于Minimax模型中的调度目标函数(式(1)),有以下推论:
在定理1中,工序加工时间可行域S的顶点是指每道工序加工时间只取其取值范围的上界或下界的自由组合所形成的一维数组s。因此,在给定调度顺序x的条件下,内层Max优化过程中的工序加工时间可行域S由
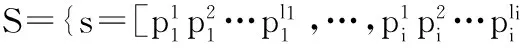
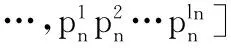
(11)
缩减为
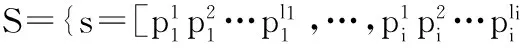
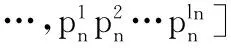
(12)
式(11)表示s内的任一元素在其加工时间取值区间内随机取值,而式(12)表示s内的任意元素的加工时间只能有两个可能取值,即取值区间的上界值或下界值。由此,通过定理1可以大幅度缩减整个工序加工时间可行域。
3 调度顺序种群和工序加工时间种群的交替进化机制
由上述Minimax问题特征分析可知:对于JSSP-PTV调度问题而言,其存在调度顺序和工序加工时间两个搜索空间,由此,在遗传算法设计时,必然存在对应的两个种群。本文采用双空间协同遗传算法,算法中的两个种群:一个表示调度顺序种群Px,一个表示工序加工时间种群Ps。在进化过程中,各种群分别利用另一个种群的当前状态来评价自身种群个体的适应度值,两种群以一种交替的方式梯度进化寻优,其交替进化过程参见图1。
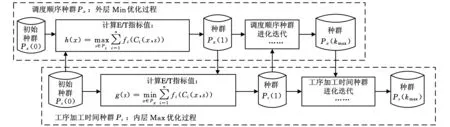
图1 调度顺序和工序加工时间双种群的交替进化示意图
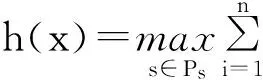
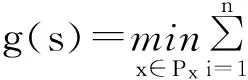
表2为两个种群寻优的示例。在调度顺序种群{x1,x2,x3}中,h(x1)的目标函数值8最小,因此,依据该种群的Min优化方向,则个体x1在进化过程中更容易保留下来;在工序加工时间种群{s1,s2,s3}中,g(s3)的目标函数值8最大,依据该种群的Max优化方向,则个体s3在进化的过程中更容易保留下来。因此,该Minimax问题在进化过程中能找到最优解为(x1,s3)。
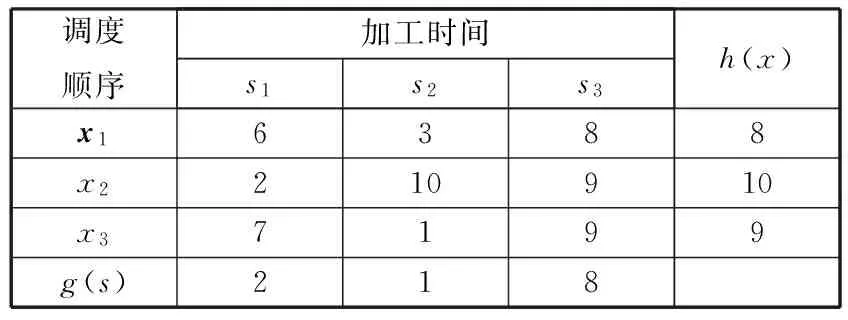
表2 Minimax问题寻优示例
4 双空间协同遗传算法(TSC-GA)
根据Minimax问题具有的“双空间寻优”特性、内层Max优化过程的凸函数定理(定理1),以及上述调度顺序和工序加工时间两个种群的交替进化机制的分析,提出了如图2所示的包括调度顺序和工序加工时间两个寻优空间的双空间协同遗传算法框架。
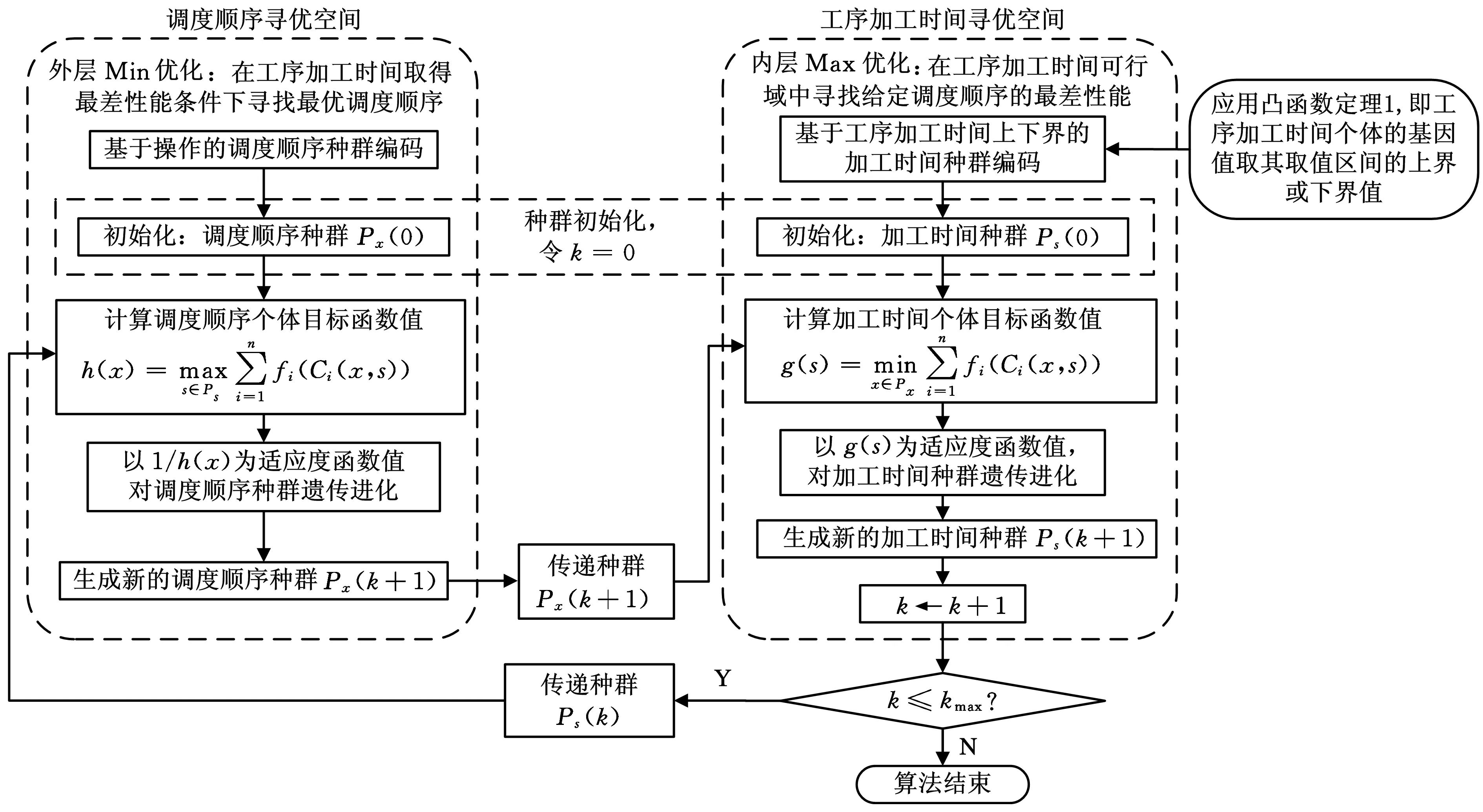
图2 双空间协同遗传算法逻辑框图
图2的处理逻辑如下:
(1)初始化。随机产生调度顺序种群Px(0)和加工时间种群Ps(0),令k=0,kmax=100。
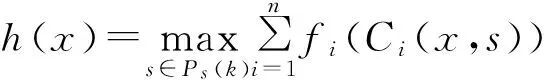
(3)调度顺序种群进化操作。以1/h(x)为适应度函数,对Px(k)进行复制、交叉和变异操作,产生新种群Px(k+1)。
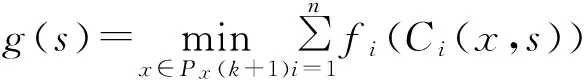
(5)加工时间种群进化操作。以g(s)为适应度函数,对Ps(k)进行复制、交叉和变异操作,产生新种群Ps(k+1)。
(6)循环条件判断。k←k+1,如果k (7)算法结束。 4.1内层Max优化过程中的遗传算法设计 在外层给定调度顺序的条件下,内层Max优化过程的主要任务是在工序加工时间可行域内寻找该调度顺序对应的最大提前/拖期惩罚成本(即E/T)惩罚值。内层遗传算法的关键操作如下: (1)编码方法。工序加工时间种群采用实数编码方法[12],即工序加工时间个体中的基因值表示对应工序加工时间的某一样本值,这种编码可以直接在解的表现上进行遗传操作。由于工序加工时间为不确定性变量,若各工序加工时间在其对应的取值之间随机取值,将导致整个搜索空间庞大。依据上述定理1的结论可知:工序加工时间个体中的基因值可只取其对应取值区间的上界值或下界值,从而大幅度压缩调度搜索空间。 (2)交叉操作。工序加工时间种群的交叉操作采用单点交叉法[12],即随机确定一个交叉位置,然后对换交叉点之后的基因片段。 (3)变异操作。对工序加工时间种群采用单点变异方式[12],即随机确定一个变异位置,当该位置上的基因值为对应取值区间的上界值时,则变异为下界值;否则,变异为上界值。 (4)选择操作。为提高遗传算法的收敛速度,选择操作采用保优策略,即经过交叉、变异后得到的新种群,和交叉、变异前的种群组合成一个大种群,计算大种群中每个个体的适应度函数值,选取适应度值大的个体组成遗传算法进化后的新种群。 4.2外层Min优化过程的遗传算法设计 在当前工序加工时间种群取得最差性能的条件下,外层Min优化过程的主要任务是在调度顺序种群内寻找最差性能值最小的调度顺序方案。外层遗传算法的主要操作如下: (1)编码方法。调度顺序个体采用基于操作的编码方式[12],即将每个染色体用n×m个代表操作的基因组成,其中各工件号均出现m次。这种编码方式的个体不仅保证了工艺约束条件,而且其任意基因串的置换排序均能表示可行调度,遗传操作过程中不会产生非法解。对应的解码过程参见文献[12]。 (2)交叉操作。调度顺序种群采用基于POX的交叉算子操作[13];这种交叉方式得到的子代能很好的继承父代优良特征,且子代总是可行的。 (3)变异操作。变异采用两点互换变异操作[12],即随机交换两不同位置上的不同基因。 (4)选择操作。同上。 5.1JSSP-PTV仿真算例 每一工件的提前和拖期惩罚系数从离散均匀分布[1,3]中随机取值。 TSC-GA算法的相关试验参数为:两个种群规模均为40,交叉概率均为0.8,变异概率均为0.2,整个算法的最大迭代次数kmax=100。仿真环境为:Windows XP Professional操作系统,CPU2.8 GHz,内存2.0 GB,仿真工具采用MATLAB2010。 为详细分析TSC-GA算法优化JSSP-PTV问题时的有效性,取β1=0.2、β2=0.4中一个具体的5×3(n×m)问题进行详细仿真分析,具体参数如表3所示。 表3 JSSP-PTV问题的5×3(n×m)算例数据 5.2TSC-GA算法求解Minimax调度模型的震荡收敛性分析 由前述的Minimax问题特征分析可知,Minimax优化过程包括最小化和最大化两个相反的优化进程,因此,其收敛过程必然具有震荡收敛趋势。以上述5×3的JSSP-PTV问题为例,TSC-GA算法求解Minimax调度模型的收敛曲线如图3所示。 图3 调度顺序种群和工序加工时间种群的协同进化曲线 首先进行震荡收敛性验证。从图3可以看出,TSC-GA算法的进化过程为一个震荡收敛曲线,有下降过程和上升过程,但最终趋于收敛。在下降过程中:外层调度顺序种群进化速度快于内层工序加工时间种群的进化速度,此时外层Min优化过程起主导作用;在上升过程中:内层工序加工时间种群进化速度快于外层调度顺序种群的进化速度,此时内层Max优化过程起主导作用。因此,由于遗传算法固有的随机性特征,使得外层和内层两个优化空间的进化速度不一致,从而使得Minimax调度问题具有显著的震荡收敛特性。 然后,对双空间协同遗传算法收敛性进行分析:双空间协同遗传算法基于一种交替进化的思想,内层Max优化和外层Min优化过程是交替并列进行寻优的,内层Max优化过程利用外层的调度顺序种群评价自身个体适应度,指导自身种群进化方向;外层Min优化过程利用内层的工序加工时间种群评价自身个体适应度,指导自身种群进化方向。因此,内层Max优化过程和外层Min优化过程都有自身单独进化时种群的最优值,虽然两条曲线有各自的进化轨迹,但当算法整体收敛时,即找到最优调度顺序及对应取到最差性能值的工序加工时间时,两曲线必然收敛到一起。 5.3工序加工时间过滤机制及算法有效性验证 为了验证基于凸函数定理(定理1)的工序加工时间可行域过滤机制对内层Max优化过程的有效性,采用与5.2节相同的调度算例进行仿真试验。当外层遗传算法给定一个调度顺序后,Minimax调度模型中的式(1)将转化为单一的Max优化问题。为保证算例的连续性及方便相关结果的分析,取5.2节中寻优结果得到的调度顺序[5 3 2 2 2 3 5 1 5 1 4 3 4 1 4]进行分析。图4所示为在该调度顺序条件下,内层遗传算法在运用工序加工时间可行域过滤机制(即工序加工时间随机变量仅取区间的上下界)和未运用过滤机制(即工序加工时间变量随机取值)两种情况下的进化曲线图。 图4 给定调度顺序条件下内层Max进化曲线 下面对工序加工时间过滤机制有效性进行验证分析。从图4可以看出,在相同迭代次数情况下,曲线1的E/T值大于曲线2的值;另外,曲线1在第5代就收敛至最大值387,而曲线2在内层遗传算法超过最大迭代次数时仍未收敛到最大值。因此,曲线1在求解质量和求解效率两方面明显优于曲线2。分析其原因如下:由于在给定调度顺序条件下,内层Max优化方向是E/T指标值越大越好;而凸函数定理1将工序加工时间的取值限定在其取值区间的上界或下界,因此内层遗传算法只需在各工序加工时间取上下界所形成的可行域内寻优,从而避免了遍历或枚举工序加工时间取值区间所消耗的大量计算时间。因此,基于凸函数定理1的工序加工时间过滤机制显著改善了内层Max过程的优化效率和解的质量。 接着,对双空间协同遗传算法有效性进行验证。图4中调度解的最大化进化过程收敛到最大值387,与5.2节中图3的结果一致,说明双空间协同进化遗传算法能够得到调度解的真实最差性能值(387);图5中的曲线1为同上的调度解[5 3 2 2 2 3 5 1 5 1 4 3 4 1 4]对应的内层Max寻优进化曲线,其他曲线为随机选取的100个调度顺序所对应的内层Max寻优进化曲线,从图中可以看出,曲线1收敛的最大E/T指标值(387)最小,其他曲线收敛值都在曲线1之上,所以,通过本文所设计双空间协同遗传算法求解Minimax调度问题,能够得到最差性能最优的调度顺序。即双空间协同遗传算法能够准确求得Minimax模型的调度解。 图5 调度顺序的内层max进化曲线对比图 5.4Minimax调度解的鲁棒性及算法高效性验证 5.4.1Minimax调度解鲁棒性验证 在工序时间不确定条件下,调度最终方案是一个调度顺序。为了验证Minimax调度模型的鲁棒性,即已得到的调度顺序的E/T性能指标在工序加工时间实际随机取值情况下仍保持较优的性能值,针对与5.2节相同的JSSP-PTV调度算例和参数,选择两个调度顺序结果,一个是利用本文提出的TSC-GA算法求解Minimax调度模型所获得的调度顺序方案(Minimax调度解),另一个是对各个工序加工时间随机变量分别取其期望值,形成一个确定性调度问题,并利用本文的遗传算法对其进行求解而获得一个调度顺序方案(期望模型调度解);然后,针对已知的两个调度顺序,在工序加工时间值域内随机取值,共进行5000次试验,二者的E/T指标值的分布参见图6、图7。 图6 Minimax调度解在工序加工时间随机取值条件下的E/T性能分布 图7 期望模型调度解在工序加工时间随机取值条件下的E/T性能分布 图6和图7中的黑点表示5000次试验中,各调度方案对应的最差性能点(即E/T指标的最大值)。从图6可以看出:5000个样本的所有指标都在TSC-GA算法求解Minimax调度模型获得的性能界(387)以内,由此证明了在工序加工时间不确定环境下,应用凸函数定理(定理1)显著压缩调度搜索空间后,能保证样本的性能指标始终在Minimax调度解对应的最差性能边界内。另外,对比图6和图7中的最差性能点可以发现:在工序加工时间随机取值条件下,Minimax调度解对应的最差性能(E/T为362)小于期望模型调度解在相同试验下所得到的最差性能(392),因此,对于Minimax调度解和期望模型调度解对应的两个调度顺序而言,前者的E/T性能在工序加工时间随机取值情况下仍保持了相对较优的性能,即Minimax调度解的鲁棒性能较好。 5.4.2双空间协同遗传算法高效性验证 表4 最差性能偏移率AWI试验结果 由表4的仿真数据可知: (1)AWI指标始终为负值,说明工序加工时间在其取值区间内随机取值时,Minimax调度解对应的最大E/T指标值均优于期望模型调度解对应的最大E/T指标,这说明Minimax调度解在不同调度规模、不同工序加工时间取值范围条件下,其E/T指标值仍保持相对较优水平,因此,Minimax模型调度解的鲁棒性始终要优于期望模型调度解,采用Minimax模型能更好的应对不确定性因素的随机扰动。 (2)所有算例中,T1的值都小于T2,说明TSC-GA的求解效率显著高于TGAI,这是由两种算法的求解机制所决定的:首先,TGAI算法中,对于外层调度顺序种群中的每个调度顺序个体,寻优其对应的最差性能值都需要调度一个完整的内层Max遗传算法,即内层工序加工时间种群进行连续多次迭代寻优,因此外层调度顺序种群进化一代都会导致内层Max过程耗费大量时间,所以两层嵌套机制寻优效率低;其次,很多调度顺序个体在遗传算法的选择操作时由于适应度函数值差会被舍弃,对于这些被舍弃的个体,前期通过完整内层遗传算法求其目标函数值所花费的计算时间都是无用功,故TGAI寻优效率进一步降低。而TSC-GA算法进化过程中每次都是单次迭代,两种群个体的目标函数值都逐步向各自的最优解靠拢,在交替进化的过程中如果已经出现了适应度函数值很差的个体,通过选择机制会将其舍去,不需要再花费多余的计算时间对其寻优,因此相对于TGAI,TSC-GA算法的求解效率显著提高。 (1)针对带有E/T非正规指标的不确定作业车间调度问题,提出并证明了有效过滤调度搜索空间的凸函数定理,即在给定调度顺序的条件下,所有工件E/T指标的最大值在工序加工时间可行域的顶点处取得;并依据此定理将工序加工时间种群中的个体取值限定在其取值区间的上界或下界,有效避免了因遍历或枚举各工序加工时间的全部值域所耗费的大量计算代价,从而显著提升了调度算法的搜索效率。 (2)针对Minimax问题存在的双空间寻优特性,提出了一种调度顺序种群和工序加工时间种群的交替进化机制,即在外层给定调度顺序的条件下,内层Max优化过程的主要任务是在工序加工时间可行域内寻找该调度顺序对应的最大E/T指标值;而在当前工序加工时间种群取得最差性能的条件下,外层Min优化过程的主要任务是在调度顺序种群内寻找最差性能值最小的调度顺序方案。 (3)不确定调度问题必然与调度决策者的喜好、决策风格密切相关,而Minimax方法属于一类保守、稳健的决策分析方法,它可以在已知信息量少、扰动因素复杂等工况下定量得到调度指标的性能界,从而为调度决策者预估最差工况及其性能指标值、采取主动稳健的调度措施等提供支持。 [1]Pindo M L. Scheduling: Theory, Algorithms, and Systems[M]. 4ed.Berlin:Springer, 2012. [2]Goren S, SabuncuoluI. Optimization of Schedule Robustness and Stability under Random Machine Breakdowns and Processing Time Variability[J]. IIE Transactions, 2009, 42(3):203-220. [3]Lei D. IntervalJob Shop Scheduling Problems[J]. The International Journal of Advanced Manufacturing Technology, 2012, 60(1/4): 291-301. [4]Daniels R L, Kouvelis P. Robust Scheduling to Hedge Against Processing Time Uncertainty in Single-stage Production[J]. Institute for Operations Research and the Management Sciences, 1995,41(2):363-376. [5]刘琳,古寒雨,席裕庚. 加工时间不确定的Just-in-time单机鲁棒调度[J]. 控制与决策,2007,22(10):1151-1156. Liu Lin, Gu Hanyu, Xi Yugeng. Robust Scheduling in a Just-in-time Single Machine System with Processing Time Uncertainty[J]. Control and Decision, 2007,22(10):1151-1156. [6]Xu X Q, Cui W T, Lin J, et al. Robust Makespan Minimization in Identical Parallel Machine Scheduling Problem with Interval Data[J]. International Journal of Production Research, 2013,51(12):1-17. [7]Herrmann J W. A Genetic Algorithm for a Minimax Network Design Problem[J]. Technical Research Report, 1999,99(12). [8]Jensen M T. A New Look at Solving Minimax Problems with Coevolution[C]//MIC’2001-4th Metaheuristics International Conference. Porto, Portugal ,2001:103-107. [9]郑泳凌,马龙华,钱积新. SGA(Simplex-Genetic Algorithm):一类求解Minimax问题的通用算法[J].系统工程理论与实践,2002,22(12):33-38. Zheng Yongling, Ma Longhua, Qian Jixin. SGA(Simplex-Genetic Algorithm):a Universal Algorithm for Solving Minimax Problem[J]. Systems Engineering-theory & Practice, 2002, 22(12):33-38. [10]Jensen M. Finding Worst-Case Flexible Schedules Using Coevolution[C]//GECCO 2001-In Genetic and Evolutionary Computation Conference. San Francisco,USA, 2001:1144-1151. [11]同济大学数学系.高等数学(第六册)[M].北京:高等教育出版社,2007. [12]王凌.车间调度及其遗传算法[M].北京:清华大学出版社,2003. [13]张超勇,饶运清,刘向军,等. 基于POX交叉的遗传算法求解Job-Shop调度问题[J].中国机械工程,2004,15(23):2149-2153. Zhang Chaoyong, RaoYunqing, Liu Xiangjun, et al. An Improved Genetic Algorithm for the Job Shop Scheduling Problem[J]. China Mechanical Engineering,2004,15(23):2149-2153. (编辑郭伟) Minimax model and Two Space Co-evolutionary Genetic Algorithm for Job Shop Scheduling Problem Yang HonganXi ZhichengXia ChangkaiWang Jinguo Key Laboratory of Contemporary Design and Integrated Manufacturing Technology,Northwestern Polytechnical University,Xi’an,710072 For the job shop scheduling problem with processing time variability, a conservative and robust Minimax analysis method was proposed to estimate the worst scenario and its corresponding bound of scheduling performance indicator. A Minimax model was formulated based on the earli E/T penalty cost of each job. To solve the huge search space problem of traditional traversal or enumeration methods, a convex function theorem was proposed and proved, which can constrict and filter the processing time ranges effectively for a given scheduling sequence, and a kind of job processing times filtering mechanism was proposed based on this convex function theorem. Based on the feature of two space optimization in solving Minimax problem, a two space co-evolutionary genetic algorithm was designed with the consideration of the alternate evolutions between scheduling sequence population and processing time population. Finally, the test results demonstrate that both of the proposed filtering mechanism and two space co-evolutionary algorithm perform effectively. job shop scheduling; processing time variability; earliness/tardiness(E/T); Minimax; two space co-evolution 2013-11-04 国家自然科学基金资助项目(50705076);西北工业大学研究生创业种子基金资助项目(Z2013047) TP301DOI:10.3969/j.issn.1004-132X.2015.03.009 杨宏安,男,1972年生。西北工业大学机电学院副教授、博士。主要研究方向为车间调度优化、智能优化算法、制造执行系统等。席志成,男,1988年生。西北工业大学机电学院硕士研究生。夏常凯,男,1988年生。西北工业大学机电学院硕士研究生。王经国,男,1989年生。西北工业大学机电学院硕士研究生。5 仿真试验及分析
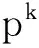
6 结论

