基于动态系数法的微型涡喷发动机实时建模

徐　鑫　张天宏　盛汉霖

南京航空航天大学江苏省航空动力系统重点实验室,南京,210016

基于动态系数法的微型涡喷发动机实时建模

徐鑫张天宏盛汉霖

南京航空航天大学江苏省航空动力系统重点实验室,南京,210016

利用时域法系统辨识获得了发动机一系列稳态点附近的转速-燃油量稳态特性和动态特性,通过插值算法获得了全范围稳态关系和加速度系数,采用动态系数法建立了发动机全范围实时模型。该模型结构简单,运算量较小,实时性好。仿真试验表明：该模型可以较好地反映微型涡喷发动机的稳态特性和动态特性，与试验数据相比，模型的稳态点误差不超过1%,过渡过程误差不超过6%，可用于微型涡喷发动机的容错控制。

微型涡喷发动机;容错控制;系统辨识;动态系数法;实时模型

0　引言

微型涡喷发动机控制系统传感器的稳定性对于保证发动机全权限数字电子控制系统正常工作至关重要[1]。针对微型涡喷发动机传感器故障诊断与容错控制的需求，本文建立了用于故障诊断的发动机实时机载模型。

目前,国内外常用的发动机建模方法有解析法和试验法[2-6]。解析法建模先根据气动热力学公式,结合部件特性和工作状态，建立发动机非线性部件级模型，再根据台架试车数据或试飞数据对其进行修正[7]。用解析法建立的模型一般比较精确,但由于算法复杂,迭代量较大,从而使得解析法建立的模型运算耗时太长,甚至导致模型运算不收敛,故不适合作为机载实时模型。试验法建模根据发动机系统的输入输出数据关系建立模型,将发动机整体看作“黑箱”或“灰箱”,传统试验法建立的模型虽然实时性较好,但模型的精度低,难以在全包线范围内模拟发动机的稳态和动态特性[8-10]。

为了建立精度高、实时性好、可在全包线范围内模拟发动机各种工况的微型涡喷发动机模型，本文在试验法的基础上,提出了一种新的建模思路[8],即根据发动机台架试车数据，运用系统辨识、插值算法和动态系数法建立微型涡喷发动机模型。由于发动机起动过程比较复杂，故本文主要研究发动机起动过程以上工作状态(起动过程模型利用最小二乘法拟合得到)。起动过程以上工作状态建模过程如下:首先利用时域系统辨识法[11-12]获得发动机一系列稳态点附近的转速-燃油流量稳态特性和动态特性，通过插值算法获得全范围稳态关系和加速度系数,采用动态系数法建立发动机全范围实时模型；然后利用实时模型对微型涡喷发动机开展从慢车状态到最大状态的数值仿真。仿真结果与原始试车数据的比较结果表明,该模型具有较好的稳态和动态精度，可以用作传感器故障诊断机载模型。

1　建模数据的获取与预处理

由于发动机具有非线性特点，所以应通过台架试验得到发动机运行过程中不同工作点的输入输出数据，试验台如图1所示。本文用油泵电压占空比来控制燃油流量，经过多次试验测试，在相同工作状态下，油泵电压占空比与燃油流量之间为固定的线性关系，故将燃油流量作为输入，将发动机转速作为输出。

图1　发动机试车台

为了准确获得发动机的动态特性，必须对其进行动态激励。本文采用的激励措施为在各个稳态工作点附近加入M序列信号。本文选取5级线性移位寄存器的M序列信号[10],其步长为0.2 s,幅值为输入信号最大幅值的5%。激励的具体实验步骤为先将发动机运行至慢车状态，之后在各个稳态工作点施加4～5个周期的M序列激励，图2所示为70 000 r/min下的动态试车曲线，转速信号的采样周期为20 ms。

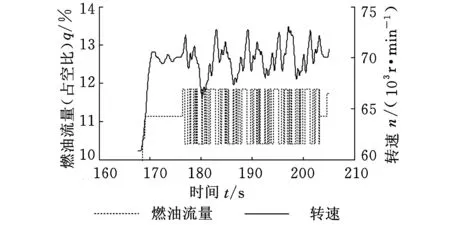
图2　发动机转速在70 000 r/min的试车数据

由试车数据可以获取各个稳态工作点的燃油流量与发动机转速稳态关系，以及稳态工作点附近的燃油流量与发动机转速动态关系。

下面利用野点剔除、滤波、相似变换以及归一化等方法对原始试车数据进行预处理。

以燃油流量为横坐标，稳态转速为纵坐标，得到发动机转速-燃油流量稳态特性曲线。参照该曲线，对明显偏离曲线的个别数据进行修正或直接舍去；对慢车以上动态曲线进行滤波处理，以提高原始试验数据的有效性。

为了建立适用于全包线范围内发动机动态仿真的数学模型,需对原始试车数据进行相似变换，将其换算至标准大气状况(p0=101 325 Pa,T0=288.15 K)下,以便将其用于不同大气条件的发动机模型计算。在环境温度为T1、环境压力为p1的大气条件下,发动机转速n、燃油流量q的换算公式如下[13]：

(1)

(2)

将得到的相似参数进行归一化处理：

ncor=nc/nc,max

(3)

qcor=qc/qc,max

(4)

式中,下标max表示最大值。

2　动态系数法

2.1动态系数的物理意义

根据微型涡喷发动机稳态转速与燃油流量的对应关系，采用一维插值法，建立其稳态模型：

(5)

式中,f(*)为一维插值函数,φ(*)=f-1(*);下标s代表稳态。

发动机在动态工作过程中,若t时刻转速为n(t),燃油流量为q(t),定义当前剩余燃油流量为

Δq=q(t)-φ(n(t))

(6)

Δq>0即燃油流量有剩余时,涡轮产生的功率大于压气机所需功率，发动机将加速;Δq<0即燃油流量减少时,涡轮产生的功率小于压气机所需功率,发动机将减速。Δq越大,发动机加速或减速得越快。由此可见，发动机的转速变化量与剩余燃油量存在某种关系，用燃油加速度动态系数C来量化此关系,即

C=Δn/(ΔqΔt)

(7)

式中,Δn为剩余燃油流量产生的转速增量；Δt为采样周期。

2.2动态系数的获取

下面采用系统辨识法推导出动态系数[9]。由于发动机内部的气动热力学过程比较复杂,为了简化发动机模型公式的推导,特作以下假设:①只考虑发动机转子惯性对发动机动态特性的影响，忽略热惯性和部件通道容积动力学的影响；②只研究发动机在其稳态点附近的小偏离运动，并认为动态过程中，部件效率及总压损失系数保持不变；③台架试车环境条件不变；④燃油泵不由发动机带动，而是由控制器驱动；⑤忽略燃烧延迟及燃气与空气流量的差别。

根据假设①,描述发动机动态特性的方程就是发动机转子的动态力矩平衡方程，即

Jdω/dt=ΔM=MT-MC

(8)

式中,J为微型涡喷发动机转子的转动惯量,kg·m2;ω为微型涡喷发动机转子的角速度,rad/s;ΔM为作用在转子轴上的外力矩之和即剩余力矩,N·m;MT为涡轮扭矩,N·m;MC为压气机扭矩,N·m。

根据微型涡喷发动机的工作原理,涡轮扭矩MT和压气机扭矩MC是转速n、燃油流量q和外界干扰量d的函数。假设d=0,则

MT=MT(n,q)

(9)

MC=MT(n,q)

(10)

对式(9)、式(10)按Talor公式展开为幂级数,并只取级数的一次项,得到线性函数，即将式(9)和式(10)在稳态点附近线性化,得

MT=MTs+ΔMT=

(11)

MC=MCs+ΔMC=

(12)

稳态时,涡轮扭矩等于压气机扭矩,即MTs=MCs=Ms。

将式(11)、式(12)代入式(8),得

(13)

为了分析方便，通常采用相对增量即参数的绝对增量与基准值之比的形式进行计算。基准值可以选取原稳定状态参数值或取最大状态稳态值等。令转速的相对增量δn=Δn/nb,燃油量的相对增量δq=Δq/qb,下标b表示基准值,将二者代入式(13),得

Td(δn)/dt+δn=Kδq

(14)

式中,T为微型涡喷发动机基本时间常数;K为微型涡喷发动机基本放大常数。

将式(14)在零初始条件下进行拉氏变换，得微型涡喷发动机的传递函数：

(15)

式(15)为微型涡喷发动机简化后最基本的数学模型。由式(15)可知，微型涡喷发动机的基本简化数学模型为无零点的一阶系统,即惯性环节。t=0、δn=0的条件下，输入δq为阶跃量时,动态方程(式(14))的解为

δn=K(1-e-t/T)δq

(16)

对式(16)两边同时求导,得

d(δn)/dt=Ke-t/Tδq/T

(17)

根据假设②,微型涡喷发动机只在原平衡状态附近做小偏离运动，原平衡状态点即为t=0的时刻。于是,式(17)可以变形为

(18)

本文通过MATLAB自带的系统辨识工具箱,将燃油流量作为输入,将转速作为输出，选择一阶惯性环节作为辨识的传递函数模型，可快速地求得T和K。则发动机当前时刻转速为

n(t)=n(t-1)+C(t)(q(t)-φ(n(t-1))Δt

(19)

式中,C(t)可由上一时刻转速n(t-1)插值得到。

在每个稳态点,利用系统辨识算法得到此状态下的T和K,根据式(18)计算出燃油加速度动态系数。将各稳态点的系数组合在一起，形成动态系数插值表(表1)，供一阶模型插值调用。

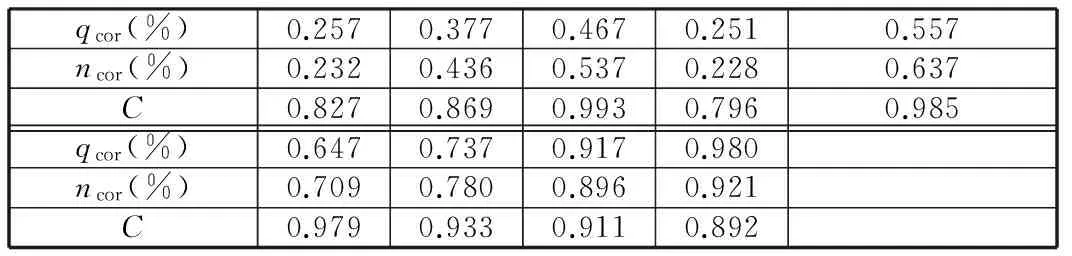
表1　动态系数插值表

3　模型仿真及结果分析

根据已得到的动态系数插值表，采用MATLAB进行编程，建立发动机数学模型。随机选取2组原始台架试车数据，对实时模型进行验证并检验建模误差。模型仿真结果如图3、图4所示。

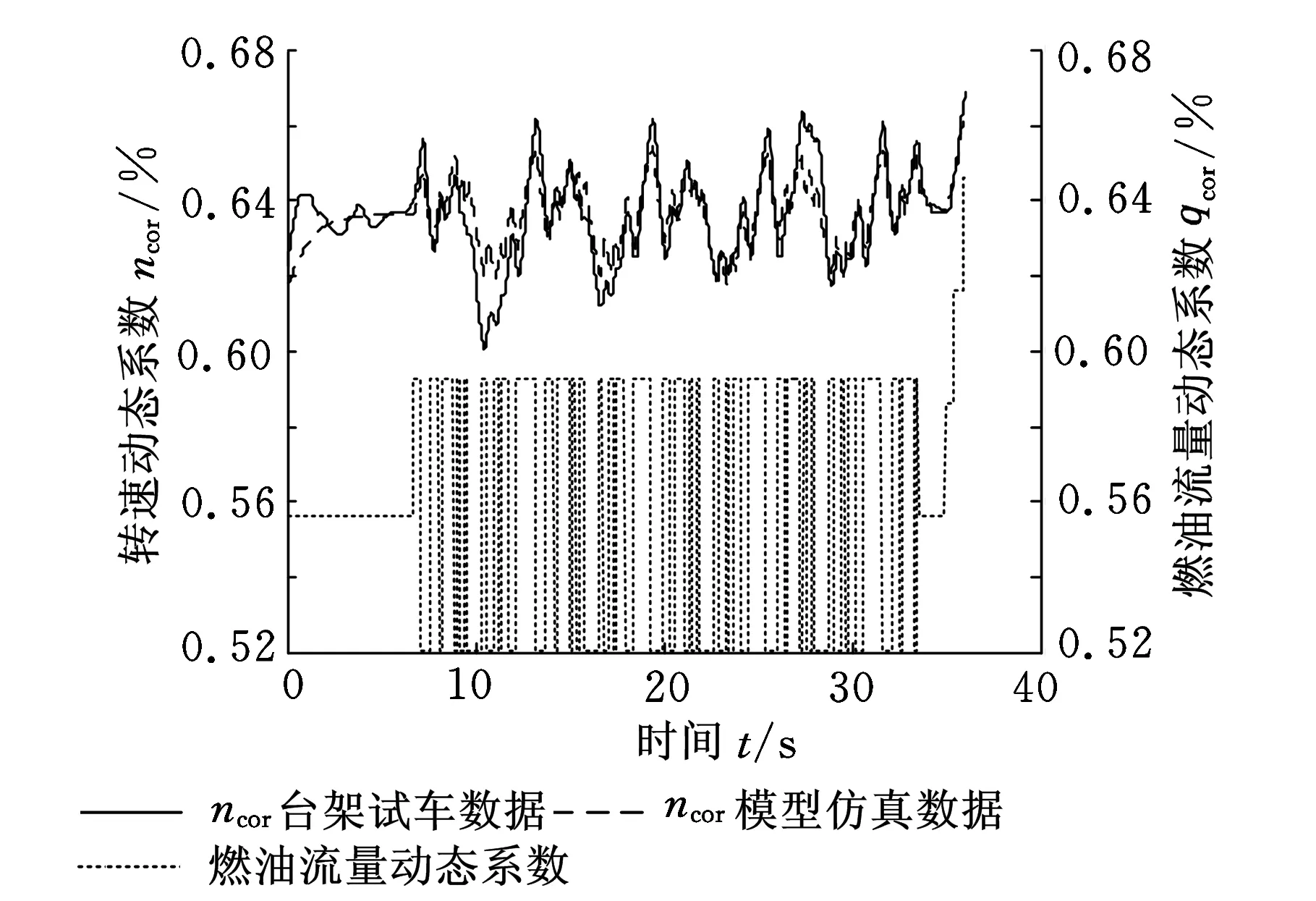
(a)仿真与试车对比曲线

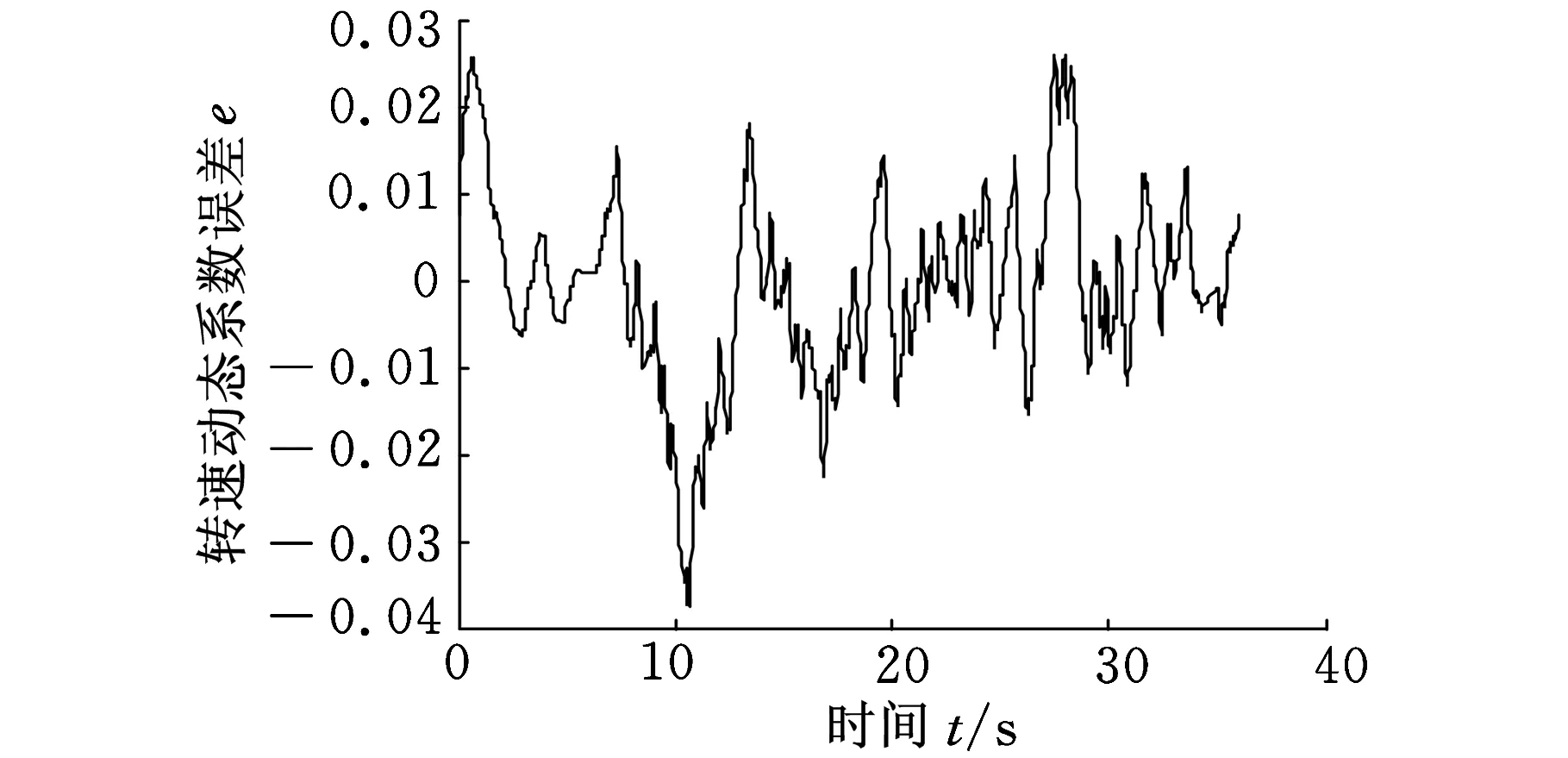
(b)误差曲线图图3　发动机模型在70 000 r/min仿真结果

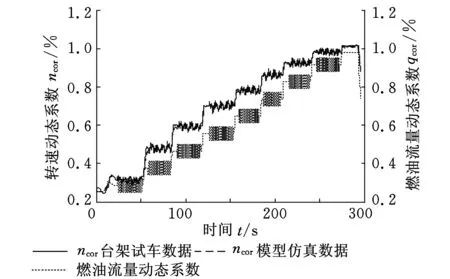
(a)仿真与试车对比曲线

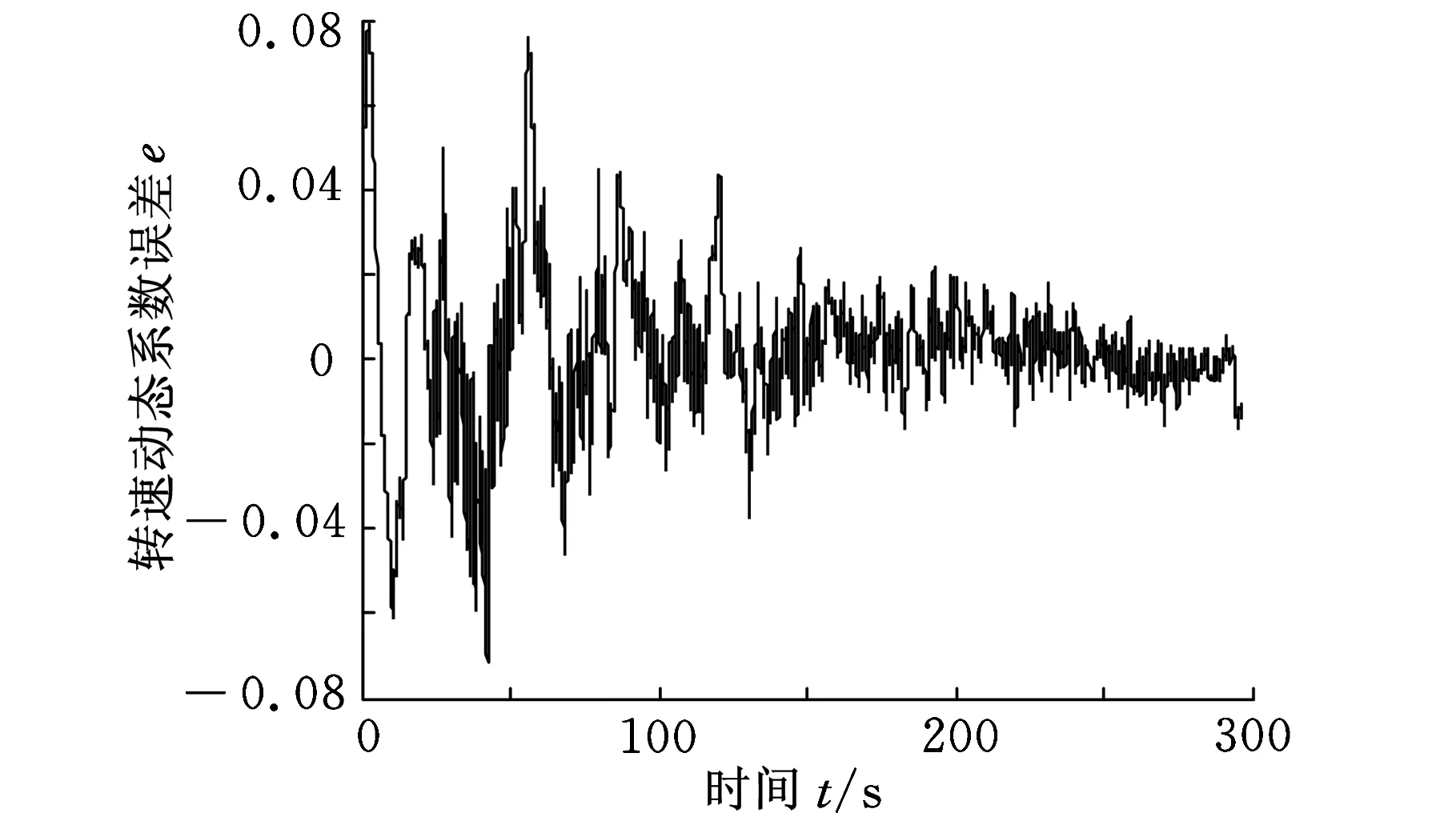
(b)误差曲线图图4　发动机模型在30 000 r/min以上仿真结果图

定义转速的仿真误差为

e=(ne-n)/n

(20)

式中,ne为各转速模型仿真值;n为转速实际采集值。

由于篇幅所限,这里只给出了部分的仿真曲线图。从图3、图4可以看出，仿真结果与试车数据一致，说明本文所采用的方法是可行的。仿真精度达到了预期要求，模型稳态点误差不超过1%，过渡过程误差不超过6%,可作为控制系统传感器故障诊断的发动机模型。

进一步将该模型嵌入到以主频100MHz的DSP芯片TMS320F2808为核心的电子控制器中进行测试，利用定时器测试出模型单步运行时间仅需0.2ms,这对于以20ms为控制步长的发动机容错控制器来说已具有极好的实时性。

4　结语

本文建立的微型涡喷发动机实时模型算法简单，采用系统辨识、插值算法和动态系数法，可有效避免传统部件级建模所必需的迭代计算，大大缩短了仿真时间，易于嵌入到发动机电子控制器中。本文采用的动态系数法可维护性强,当发动机更换或通过试验得到更精确的稳动态试验数据后，可通过本文所述的方法获得动态系数,修改插值数据满足模型更新的要求。本文只针对转速建立了发动机转速-燃油关系的动态模型，可用类似的方法针对燃气温度、推力等其他参数建立相应的模型。

[1]孙健国.面向21世纪航空动力控制展望[J].航空动力学报,2001,16(2):97-102.

SunJianguo.ProspectsoftheAeroengineControlDevelopmentintheEarlyTimeofthe21stCentury[J].JournalofAerospacePower,2001,16(2):97-102.

[2]DanieleCJ,KroselSM,SzuchJR,etal.DigitalComputerProgramforGeneratingDynamicTurbofanEngineModels,NASATM283446[R].Cleveland,Ohio:LewisResearchCenter,1983.

[3]KimJH,SongTW,KimTS,etal.ModelDevelopmentandSimulationofTransientBehaviorofHeavyDutyGasTurbines[J].JournalofEngineeringforGasTurbinesandPower,2001,12(3):589-594.

[4]李家瑞.航空发动机建模技术研究[D].南京:南京航空航天大学,2005.

[5]张建良,秦琦峰,黄向华,等.小型航空二冲程活塞发动机建模及控制器在回路仿真研究[J].中国机械工程,2013,24(7)：906-909.

ZhangJianliang,QinQifeng,HuangXianghua,etal.ResearchonModelingandECUIn-the-loopSimulatiomforTwoStrokePiston-aeroEngine[J].ChinaMechanicalEngineering,2013,24(7):906-909.

[6]LennartLjung.BlackBoxModelfromInputOutputMeasurement[C]//IEEEInstrumentationandMeasurementTechnologyConference.Budapest,Hungary,2001:21-23.

[7]GeveM.APersonalViewoftheDevelopmentofSystemIdentification[J].IEEEControlSystemsMagazine,2006,26(6):93-105.

[8]周文祥,黄金泉,黄开明.航空发动机简化实时模型仿真研究[J].南京航空航天大学学报,2005,37(2):251-255.

ZhouWenxiang,HuangJinquan,HuangKaiming.Real-timeSimulationSystemforAeroengineBasedonSimplifiedModel[J].JournalofNanjingUniversityofAeronautics&Astronautics,2005,37(2):251-255.

[9]潘慕绚,黄金泉.航空发动机模型参考自适应控制综述[J].航空发动机,2003,29(2):51-54.

PanMuxuan,HuangJinquan.SummaryofModelReferenceAdaptiveControlofAeroengine[J].Aeroengine,2003,29(2):51-54.

[10]孙建国,黄金泉,叶志峰,等.现代航空动力装置控制[M].北京:航空工业出版社,2009.

[11]于连栋，费业泰.状态变量分析法在系统辨识中的应用[J].中国机械工程，2004，15(16)：1472-1474.

YuLiandong,FeiYetai.ApplicationofAnalysisMethodofStateVariableinSystemIdentification[J].ChinaMechanicalEngineering,2004,15(16):1472-1474.

[12]倪博溢,萧德云.MATLAB环境下的系统辨识仿真工具箱[J].系统仿真学报,2006,18(6):1493-1496.

NiBoyi,XiaoDeyun.SystemIdentificationandSimulationToolboxunderMATLABEnvironment[J].JournalofSystemSimulation,2006,18(6):1493-1496.

[13]廉筱纯,吴虎.航空发动机原理[M].西安:西北工业大学出版社,2005.

(编辑张洋)

Research on MTE Real-time Modeling Based on Dynamic Coefficient Method

Xu XinZhang TianhongSheng Hanlin

Jiangsu Province Key Laboratory of Aerospace Power Systems，Nanjing University of Aeronautics and Astronautics,Nanjing,210016

This paper obtained a series of rotating speed-fuel consumption steady state and dynamic property of the engine at some steady points by using system identification method of time domain, obtained steady state relationship and acceleration coefficient for full range by using interpolation method, and established real-time model of the engine for full range by using dynamic coefficient method.This model was characterized by simple structure,small calculating amount,high real-time control.Simulation results show that this model can well reflect the steady state and dynamic property of MTE,compared to experimental data, steady point’s deviation of the model is less than 1%,deviation of transient process is less than 6%,which can apply to fault-tolerant control of MTE.

micro-turbojet engine(MTE);fault tolerant control;system identification;dynamic coefficient method;real-time model

2013-10-10

国家自然科学基金资助项目(51176075);江苏高校优势学科建设工程资助项目

V233.7DOI：10.3969/j.issn.1004-132X.2015.02.021

徐鑫,男,1989年生。南京航空航天大学能源与动力学院硕士研究生。主要研究方向为微型涡喷发动机控制器设计与容错控制。张天宏,男,1968年生。南京航空航天大学能源与动力学院教授。盛汉霖,男,1986年生。南京航空航天大学能源与动力学院博士研究生。