LS-SVM回归算法在刀具磨损量预测中的应用

关　山　闫丽红　彭　昶

1.东北电力大学,吉林,132012　　2.吉林石化工程设计有限公司,吉林,132013

LS-SVM回归算法在刀具磨损量预测中的应用

关山1闫丽红2彭昶1

1.东北电力大学,吉林,1320122.吉林石化工程设计有限公司,吉林,132013

提出了基于最小二乘支持向量机回归算法的刀具磨损量预测方法。该方法首先利用经验模态分解算法对非线性、非平稳的声发射信号进行平稳化处理，得到了若干个固有模态函数；然后建立了每个固有模态函数的自回归模型，并提取模型系数构造特征向量；最后采用最小二乘支持向量机回归算法实现了刀具磨损量的预测。该方法与神经网络预测算法相比,具有更高的预测准确率,可有效预测当前切削状态下10 s后的刀具磨损量。

刀具磨损量预测;最小二乘支持向量机;经验模态分解;自回归模型

0　引言

刀具状态监测是保障工件表面质量和尺寸精度,防止工件报废、机床损坏,优化加工过程,提高生产效率的重要手段,因此对刀具的状态进行监测具有重要的现实意义。为此，学者们提出了多种监测方法，这些监测方法多以刀具磨损状态的监测[1-6]为主,针对加工过程中刀具磨损量的实时预测尤其是在变切削条件下刀具磨损量预测的研究方法相对较少。

本文结合切削过程中声发射信号非平稳的特点,首先采用经验模态分解(empirical mode decomposition,EMD)方法[7-8]将声发射信号分解为若干个平稳的固有模态函数(intrinsic mode functions,IMF)分量,然后分别对每个IMF分量建立自回归(auto regressive,AR)模型,提取模型系数构造特征向量,最后采用最小二乘支持向量机(lease square support vector machine,LS-SVM)回归算法有效实现了变切削条件下刀具磨损量的在线跟踪预测。

1　刀具磨损实验系统及实验方法

实验系统如图1所示,传感器为PXR30谐振式声发射传感器(谐振频率为300 kHz,带宽为80～400 kHz)。较高的频率能有效接收刀具磨损信号中的高频成分，并可滤除低频噪声；较宽的频带有利于实验过程中宽频信号的采集。前置放大器为PXPAⅡ宽带声发射放大器,带宽为15～2000 kHz。采用PCI-1721数据采集卡,利用LabVIEW软件编写数据采集程序完成数据采集,采样频率为1 MHz。实验材料为高温合金 GH4169，刀片为肯纳公司的KC9125硬质合金涂层刀片，采用CKA6136i数控车床进行车削实验。

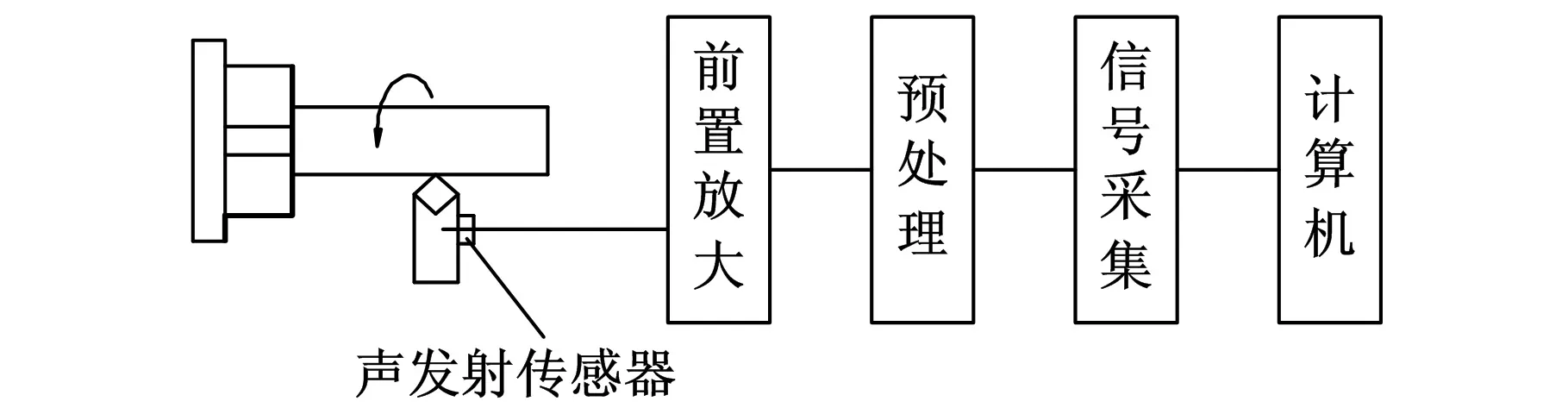
图1　声发射数据采集系统示意图

切削过程中,采用不同的切削参数(切削速度、进给量、切削深度)组合加工同一材料时，刀具的磨损率是不同的，其中，切削速度对刀具寿命的影响要远远大于进给量和切削深度对刀具寿命的影响。如果不对切削的选取做一定的限制,而是自由组合进行切削实验,然后应用同一模型进行磨损量预测,这必然会带来很大的误差。根据切削速度的选取范围，实验分3组进行，每组实验切削速度的选取范围如表1所示,进给量、切削深度的选取则不加限定。采用正交试验设计法，每组设计三因素三水平的正交试验。

表1　各组正交实验所选用的切削速度　r/min

实验中需取下刀片测量磨损量的大小,当再次将刀片安装到刀柄继续进行切削实验时,刀片的安装角度、夹紧力等的影响使得再次切削时的刀具磨损面发生变化，导致刀具的磨损位置发生变化，这与实际切削过程不符，因此采用这种数据构建的预测模型应用到实际在线监测场合会产生较大的误差。为此设计如下实验方法：

(1)取一新刀片切削10 s后停车，仅采集切削6～10 s间的数据并测量后刀面磨损量VB值(单位mm)。

(2)更换新刀片,连续切削20 s后停车，采集15～20 s间的数据,测量VB值。

(3)再次更换新刀片,切削时间比上次再增加10 s,记录切削过程最后5 s的数据,测量VB值。

(4)反复进行步骤(3),直到一次连续切削能使刀片磨损为止,切削实验结束。

(5)依据正交实验表,变换切削条件,重复步骤(1)～(4),直至完成正交实验表内规定切削条件下的切削实验。

这种实验方法与实际的连续切削过程相符。每次切削过程最后5 s的采样数据对应的正是刀具当前磨损状态,同时也减少了数据量，便于标定切削时间、刀具磨损量及信号特征之间的一一对应关系。本文仅以切削速度560 r/min、切削深度0.4 mm、进给量0.3 mm/r切削条件下取得的实验结果进行举例说明。图2中,从上至下依次为后刀面磨损量是0.11 mm、0.13 mm、0.17 mm、0.24 mm、0.26 mm、0.31 mm时的采样信号时序图。

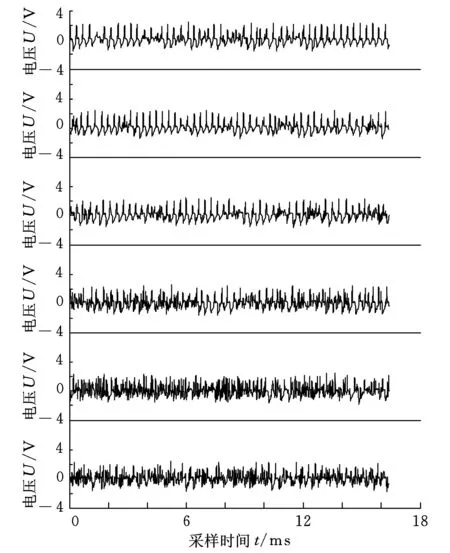
图2　不同磨损阶段采样信号时序图

2　刀具磨损信号特征的提取

2.1声发射信号的EMD分解

EMD是一种自适应、不需预先确定分解基的信号处理方法，可以将复杂的非平稳信号以有限个IMF分量之和的形式表示，EMD分解可描述为

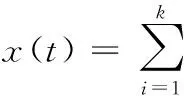
(1)

式中,x(t)为原始非平稳信号;ci(t)为从高频到低频的多个IMF分量,各IMF分量包含了原信号中不同时间尺度的局部特征信息[7-8];r为残余项;k为分量个数。

刀具磨损声发射信号具有强烈的非平稳特征,采用EMD方法对其进行分析,可以更准确、有效地把握信号特征信息。

实验数据表明:不同磨损阶段的采样信号经EMD分解后,得到IMF分量的个数是不同的，如图3a所示，当VB为0.11 mm时,采样信号经EMD分解得到11个 IMF分量，用c1(t)，c2(t),…,c11(t)表示。

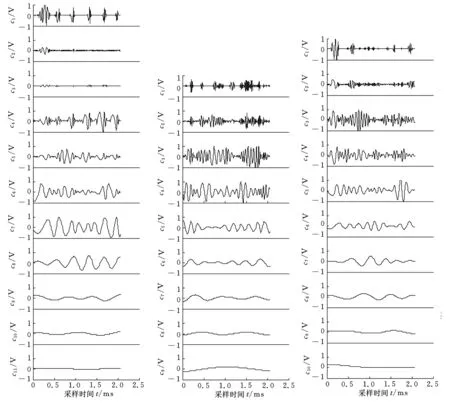
(a)VB=0.11 mm　(b)VB=0.26 mm(c)VB=0.31 mm图3　不同磨损状态信号经EMD分解后的结果

2.2EMD分解的规范化处理

计算各IMF分量与原信号的相关系数,相关系数大,说明此IFM分量包含更多的原始信号信息;相关系数小则表示此IMF分量包含的噪声成份较多，可以通过略去相关系数小的IMF分量达到降低噪声、规范化特征向量维数的目的。由图4可见,c2(t),c3(t),…,c6(t)与原始信号的相关性较大,予以保留,而c7(t)以后的各IMF分量与原信号相关性较小,忽略不计。

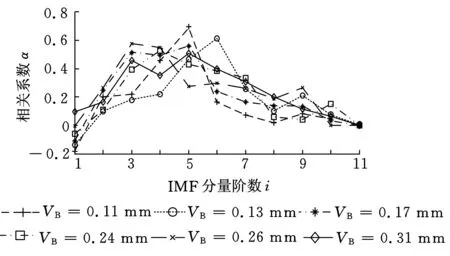
图4　各阶IMF分量与原始信号的相关性

2.3基于AR模型的刀具磨损特征提取

AR模型参数[9-10]凝聚了系统状态的重要信息,对系统状态变化的反映最为敏感。通过建立各IMF分量的AR模型达到特征提取的目的。

n阶自回归模型AR(n)可描述为

xt=φ1xt-1+φ2xt-2+…+φpxt-p+εt

(2)

式中,φk为模型系数,k=1,2,…,p;p为模型阶次；εt为模型残差。

建立AR模型的关键就是模型阶数的确定和参数的估计,本文采用最小信息准则确定模型的阶数。阶数确定后，采用最小二乘法求解模型参数。准则函数定义为

AIC(p)=Nln(σ2)+2p/N

(3)

式中,AIC(p)为p阶模型的准则函数值;σ2为模型残差的方差;N为采样数据长度。

图5为计算机求解模型最佳阶次的程序流程图,计算时先根据初定的模型阶次p求解模型参数,然后计算AIC(p),改变p值,反复计算AIC(p),AIC(p)取值最小时的p就是模型的最佳阶次。

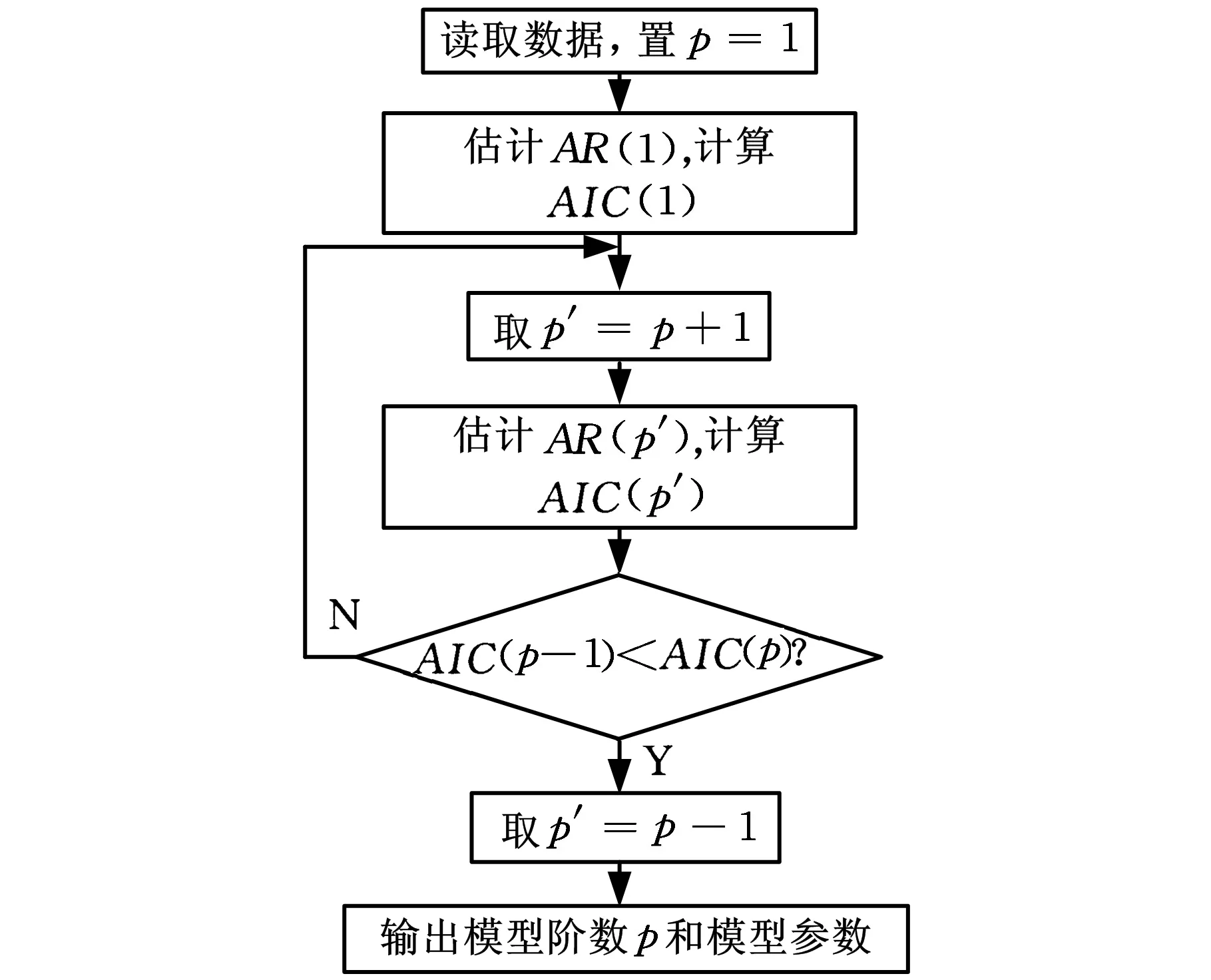
图5　计算机求解模型最佳阶次的程序流程图

建模前先对各阶IMF分量利用下式进行能量归一化处理：

(4)

以消除切削条件变化对预测结果的影响。

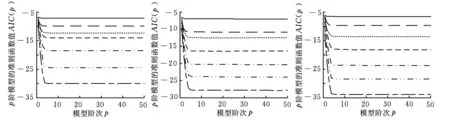
大量的实验数据计算后发现:当模型阶次p>4时,AIC(p)变化很小，因此判定4为模型的最佳阶次,如图6所示。

针对每个IMF分量,根据确定的最佳阶次,利用最小二乘法求解模型系数,建立4阶模型。并采用一步预测法检验所建模型的准确性,图7为VB=0.12 mm时的预测结果和预测误差的图解表示。

(a)VB=0.11 mm(b)VB=0.26 mm(c)VB=0.31 mm

图6AIC(p)随阶次的变化情况图

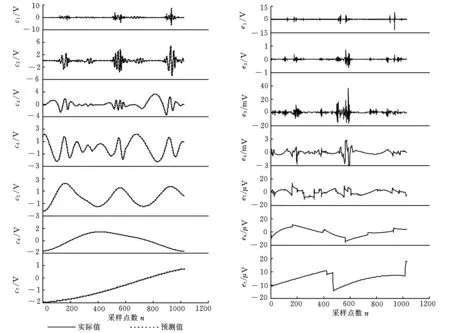
(a)实际值与预测值曲线(b)误差曲线图7　AR(4)模型的预测值及预测误差值曲线

提取各IMF分量的系数组成28维特征向量：

T=(φ1,1,φ1,2,φ1,3,φ1,4,…,φ7,1,φ7,2,φ7,3,φ7,4)

(5)

式中,φi,j为第i个IMF分量建立4阶AR模型后的第j个系数。

3　LS-SVM回归算法的磨损量预测[11]

训练数据集S={(xi,yi)|i=1,2,…,l},第i个样本的输入值为xi=(xi1,xi2,…,xi n),yi∈R为xi对应的目标值。回归的目的是根据已知的训练数据去寻找一个实值函数y=f(x),以便能用该函数推断任意x所对应的y值,具体算法参见文献[12]。

根据本文所述的实验方法、特征提取方法,建立表2所示的切削时间、特征向量、磨损量大小的对应关系，n次切削实验为在相同的切削条件、相同实验材料下完成，实验次数n由刀具的实际磨损程度决定。

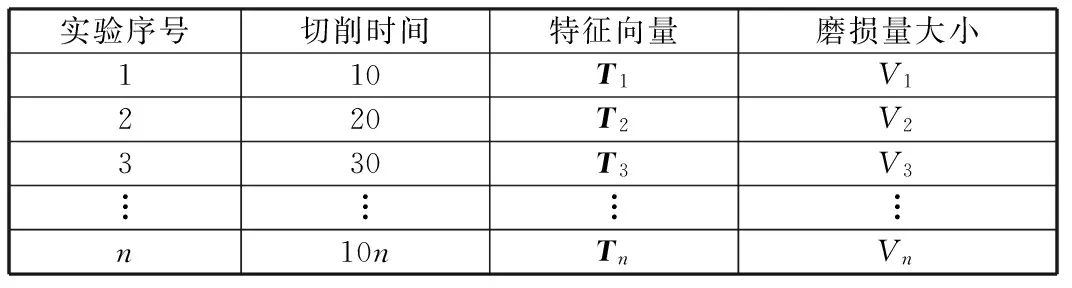
表2　切削时间、特征向量、刀具磨量对应关系

根据表2构造训练样本集：

(6)

(7)

式中,X为由特征向量构造的特征向量矩阵;Y为由磨损量构造的列矩阵。

利用式(5)所示的输入、输出进行支持向量机的回归训练，以实现刀具当前状态磨损量的估算；式(6)可实现当前状态10s后刀具磨损量的预测。

为了比较LS-SVM回归算法在刀具磨损量预测中的性能,采用文献[1]所述的BP网络,以相同的样本进行训练,并对刀具磨损量进行预测,结果如图8、图9所示。

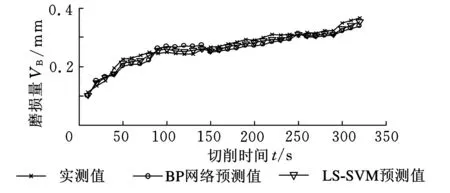
图8　磨损量实测值与预测值对比

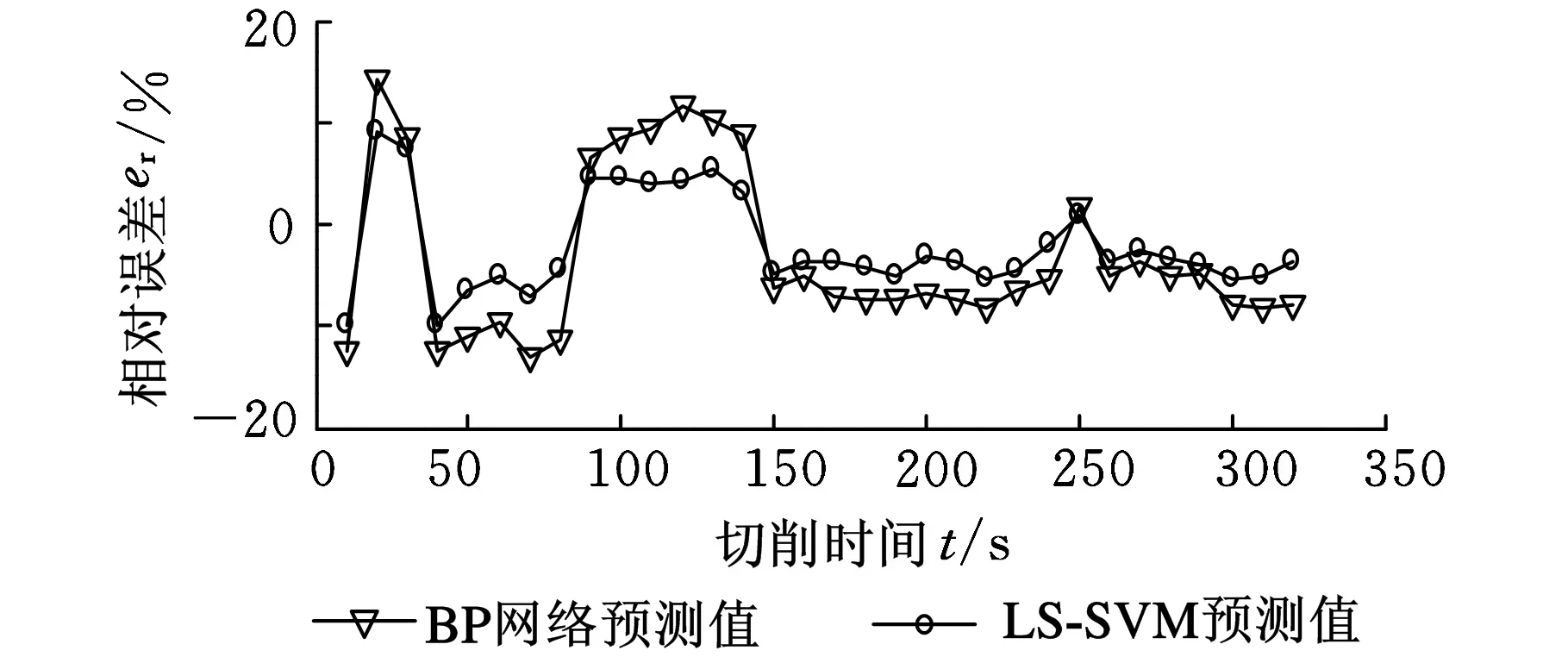
图9　采用不同预测算法相对预测误差对比

如图8、图9所示,采用LS-SVM回归算法进行刀具磨损量预测时,在刀具的初期磨损阶段,预测结果相对误差较大,最大相对误差为-9.821%。进入正常磨损阶段后,相对误差显著减小,且波动相对平稳。这是因为即使切削条件、切削材料、切削时间等完全一致,刀具后刀面的磨损量也是有差异的。采用工具显微镜测量后刀面磨损量时也发现,后刀面的磨损量也并不均匀,在选取测量位置时存在很大的人为因素。以上现象在刀具初期磨损阶段表现得尤为明显,因为新刀片表面粗糙度较大，并可能存在显微裂纹、氧化或脱碳等缺陷，而且切削刃锋利，后刀面与加工表面接触面积较小，压应力较大，所以容易磨损。

采用LS-SVM回归算法进行刀具磨损量预测的精确度要远远高于L-M优化算法BP网络的预测准确率。采用本文提出的实验方法及输入、输出的构造方式，完全可以实现更长时间的刀具磨损量预测，但这要根据刀具的实际磨损率进行确定,如切削高温合金GH4169,刀具的磨损是非常剧烈的，所以在切削实验时,切削时间仅比上一次增加10s,采用式(6)进行回归估计,得到的回归函数将能实现对刀具当前状态下未来10s后刀具磨损量的预测。

[1]关山,聂鹏.L-M优化算法BP网络在刀具磨损量预测中的应用[J].机床与液压,2012,40(15):22-26.

GuanShan,NiePeng.ApplicationofImprovedL-MOptimizationAlgorithmBPNeuralNetworkinToolWearPrediction[J].MachineTool&Hydraulics,2012,40(15):22-26.

[2]王国锋,李启铭,秦旭达,等.支持向量机在刀具磨损多状态监测中的应用[J].天津大学学报,2011,49(1):35-39．

WangGuofeng,LiQiming,QinXuda,etal.ApplicationofSupport-vectorMachineinToolWearofMulti-stageMonitoring[J].JournalofTianjinUniversity,2011,49(1):35-39.

[3]王计生,喻俊馨,黄惟公.小波包分析和支持向量机在刀具故障诊断中的应用[J].振动、测试与诊断,2008,28(3):273-276．

WangJisheng,YuJunxin,HuangWeigong.ApplicationofWaveletPackageAnalysisandSupportVectorMachinetoFaultDiagnosisofCuttingTool[J].JournalofVibration,Measurement&Diagnosis,2008,28(3):273-276.

[4]ZhuKunpeng,WongYokeSan,HongGeokSoon.WaveletAnalysisofSensorSignalsforToolConditionMonitoring:AReviewandSomeNewResults[J].InternationalJournalofMachineTools&Manufacture,2009,49(7):537-553．

[5]DuttaS,DattaA,DasChakladarN,etal.DetectionofToolConditionfromtheTurnedSurfaceImagesUsinganAccurateGreyLevelCo-occurrenceTechnique[J].PrecisionEngineering,2012,36(3):458-466．

[6]ZhuKunpeng,YokeSanWong,GeokSoonHong.Multi-categoryMicro-millingToolWearMonitoringwithContinuousHiddenMarkovModels[J].MechanicalSystemsandSignalProcessing,2009,23(2):547-560．

[7]HuangNE,ShenZ,LongSR,etal.TheEmpiricalModeDecompositionandtheHilbertSpectrumforNonlinearandNon-stationaryTimeSeriesAnalysis[J].ProceedingsoftheRoyalSocietyofLondonSeriesA:MathematicalandPhysicalSciences,1998,454:903-995.

[8]刘立君,王奇,杨克已,等.基于EMD和频谱校正的故障诊断方法[J].仪器仪表学报,2011,32(6):1278-1283.

LiuLijun,WangQi,YangKeji,etal.EMDandSpectrumCorrection-basedFaultDiagnosisMethod[J].ChineseJournalofScientificInstrument,2011,32(6):1278-1283.

[9]周云龙,王锁斌,刘永奇.自回归和EMD用于离心式风机不对中故障分析[J]．振动、测试与诊断,2011,31(5)： 582-585．

ZhouYunlong,WangSuobin,LiuYongqi.ApplicationofEMDandAuto-regressiveModelinCentrifugalFanMisalignmentFaultAnalysis[J].JournalofVibration,Measurement&Diagnosis,2011,31(5):582-585.

[10]吴森,韦灼彬,王绍忠,等.基于AR模型和主成分分析的损伤识别方法[J].振动、测试与诊断,2012,32(5):841-845.

WuSen,WeiZhuobin,WangShaozhong,etal.DamageIdentificationBasedonARModelandPCA[J].JournalofVibration,Measurement&Diagnosis,2012,32(5):841-845.

[11]王利伟，王姣．云-SVM模型及在数控机床刀具磨损状态预测中的应用[J]．组合机床与自动化加工技术，2012(9):25-27．

WangLiwei,WangJiao.Cloud-SVMModelandItsApplicationinthePredictionofCNCMachineToolWearState[J].ModularMachineTool&AutomaticManufacturingTechnique，2012(9)：25-27.

[12]郭新晨．最小二乘支持向量机算法及其应用研究[D]．吉林：吉林大学，2008．

(编辑张洋)

Application of Regression Algorithm of LS-SVM in Tool Wear Prediction

Guan Shan1Yan Lihong2Peng Chang1

1.Northeast Dian Li University,Jilin,Jilin,132012 2.Jilin Petor Chemical Engineering Co., Ltd., Jilin,Jilin,132013

Aiming at online predicting tool wear accurately,a method based on the regression algorithm of LS-SVM was proposed.First the acoustic emission signals were decomposed into several intrinsic mode functions(IMF) employing empirical mode decomposition.Then,an AR model of each IMF was established respectively.AR model coefficients were extracted to construct feature vector.Finally,the feature vectors were feed into LS-SVM and prediction of tool wear was realized.The experimental results show that it can predict the amount of tool wear after 10s according to the current cutting conditions and the proposed method has better accuracy compared with neural network algorithm.

tool wear prediction;lease square support vector machine(LS-SVM);empirical mode decomposition(EMD);auto regressive(AR) model

2013-09-22

东北电力大学博士科研启动基金资助项目(BSJXM-201115)

TH165.3DOI：10.3969/j.issn.1004-132X.2015.02.016

关山,男,1970年生。东北电力大学机械工程学院教授。主要研究方向为机械设备故障诊断。发表论文20余篇。闫丽红,女,1970年生。吉林石化工程设计有限公司高级工程师。彭昶,男,1989年生。东北电力大学机械工程学院硕士研究生。