电子齿轮箱精度控制与实验研究

田晓青　韩　江　夏　链

合肥工业大学,合肥,230009

电子齿轮箱精度控制与实验研究

田晓青韩江夏链

合肥工业大学,合肥,230009

研究了电子齿轮箱的实现原理及其在数控系统中的实现方法,从几何角度分析了齿轮展成法加工误差产生的原因,并推导出电子展成误差的计算公式。建立了电子齿轮箱仿真模型,通过对模型的仿真分析和优化,计算得到了该控制模型的电子展成误差。将该模型用于六轴数控系统实验平台,在空载条件下分析了电子展成误差。最后将自主研发的带电子齿轮箱的滚齿数控系统应用于YS3118数控滚齿机,通过齿轮加工及检测证明了该电子齿轮箱的控制精度满足齿轮的加工要求。

电子齿轮箱；滚齿；展成；前馈

0　引言

20世纪90年代,国内有诸多学者[1-5]研究了电子齿轮箱的实现方法,但普遍基于国外数控系统[6-9],不具有良好的开放性,致使无自主产权的电子齿轮箱应用于齿轮加工行业。

本文研究了电子齿轮箱的实现方法,并详细说明了电子齿轮箱在数控系统中的实现过程。通过对电子齿轮箱误差产生的几何分析,推导出电子齿轮箱展成误差的计算公式。在MATLAB中建立了电子齿轮箱仿真模型,通过对模型的仿真分析和优化,计算得到了该控制模型的电子展成误差。在确保电子齿轮箱控制模型具有良好跟踪性能的情况下,将优化的模型应用于自制的六轴数控系统实验平台,在空载条件下分析了电子展成误差。最后,将自主研发的带电子齿轮箱的数控系统应用于YS3118数控滚齿机,通过加工齿轮及检测,得到了电子齿轮箱控制的最终加工误差。结果表明,在该电子齿轮箱的控制下所加工的齿轮满足要求，具有较高精度。

1　电子齿轮箱控制原理

1.1滚齿机传动原理

滚齿加工是利用滚刀与工件毛坯之间的展成运动来实现的[10]。滚齿加工过程中,刀具节曲线与工件节曲线之间保持纯滚动[11-12]。这种纯滚动关系在传统数控滚齿机床中是依靠复杂的机械传动链及挂轮机构来实现的。

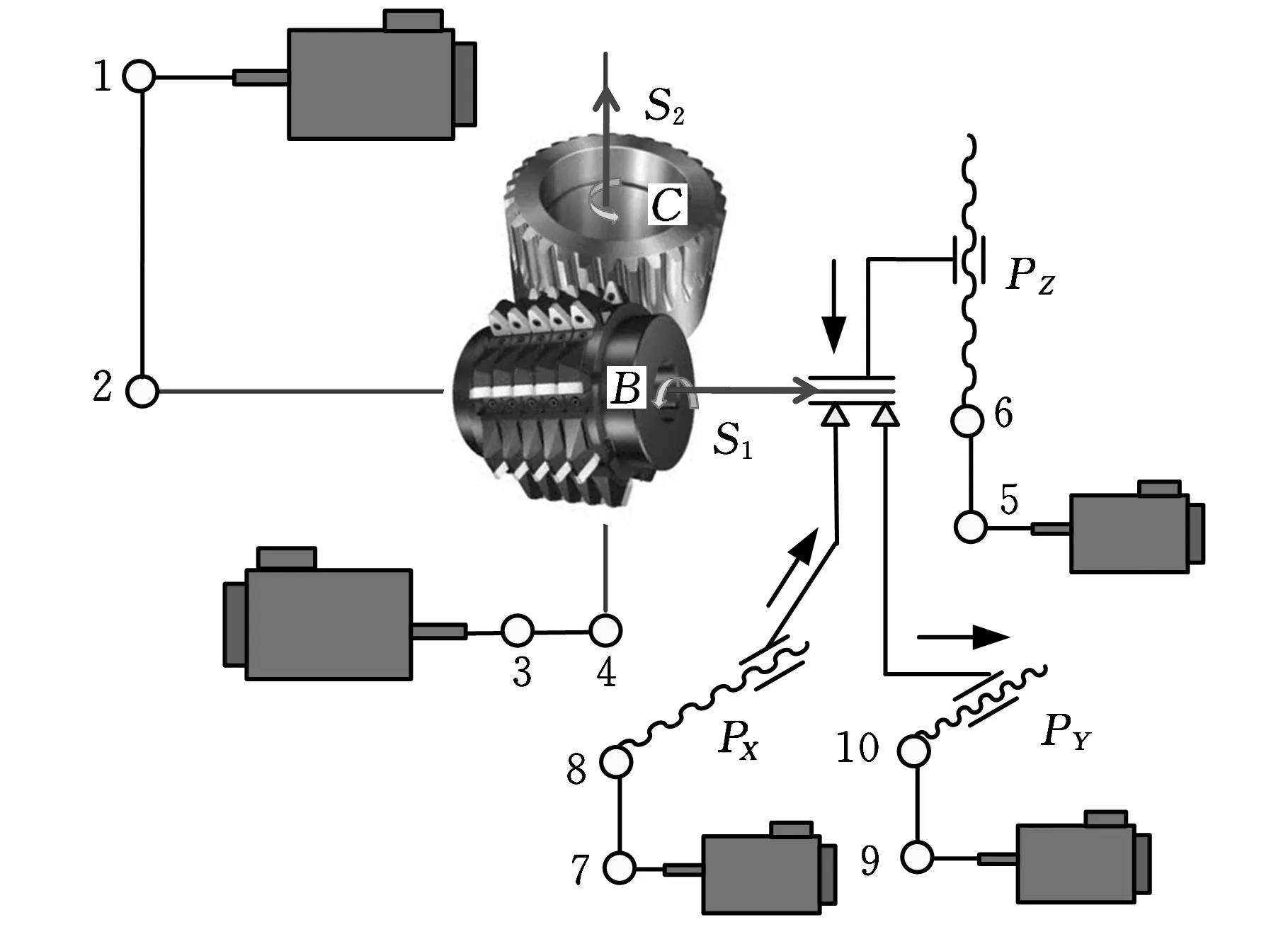
图1　全数控滚齿机传动原理

全数控滚齿机床用电子齿轮箱取代复杂的内联传动链,完成齿轮滚切所需要的展成和差动运动。如图1所示,刀具轴与工件轴是2个独立的数控轴,其展成和差动关系依靠电子齿轮箱软件控制实现。因此,电子齿轮箱的控制精度直接决定齿轮的加工精度。

1.2电子齿轮箱的实现原理

通常,六轴数控滚齿机的数控轴分别为径向进给轴(X轴)、刀具窜动轴(Y轴)、轴向进给轴(Z轴)、滚刀安装角度调整轴(A轴)、滚刀回转轴(B轴)、工件回转轴(C轴)。滚刀与工件之间的展成和差动关系为

(1)

式中,nC为C轴的转速,r/min;ZB为滚刀的头数;ZC为工件齿轮的齿数;vY、vZ分别为Y轴、Z轴的移动速度,mm/min;β为工件螺旋角,(°);λ为刀具的安装角,(°);mn为齿轮的法向模数,mm;KB、KZ、KY均为系数。

工件螺旋角为右旋时,β>0;工件螺旋角为左旋时,β<0。滚刀螺旋角γ>0(右旋)时,KB=1;滚刀螺旋角γ<0(左旋)时,KB=-1。vZ<0,β>0时,KZ=1;vZ<0,β<0时,KZ=

-1。vZ>0,β>0时,KZ=-1;vZ>0,β<0时,KZ=1。vY>0时,KY=1;vY<0时,KY=-1。

如式(1)所示,当加工直齿轮即工件螺旋角β为0时,B轴与C轴的速比为常数;当加工斜齿轮时,C轴需附加由刀具沿Z轴运动而产生的转动;当刀具有沿Y轴的窜动时,C轴需要有刀具Y向移动产生的附加转动。

电子齿轮箱的控制指令含有滚刀头数、滚刀螺旋升角、工件齿数、工件模数和工件螺旋角5个参数。电子齿轮箱的控制原理如图2所示，其中包含电子齿轮箱打开指令和关闭指令的处理过程。当零件程序含有电子齿轮箱打开控制指令时，数控系统在进行常规控制[13]的同时,还需实时采集主轴速度信号、Z轴速度信号和Y轴速度信号,并将这些信息在每个插补周期传递到加减速处理之前的数据结构中(C轴的速度指令是根据式(1)计算得到的),再经过加减速控制、粗插补、精插补和位置控制完成对C轴的控制。

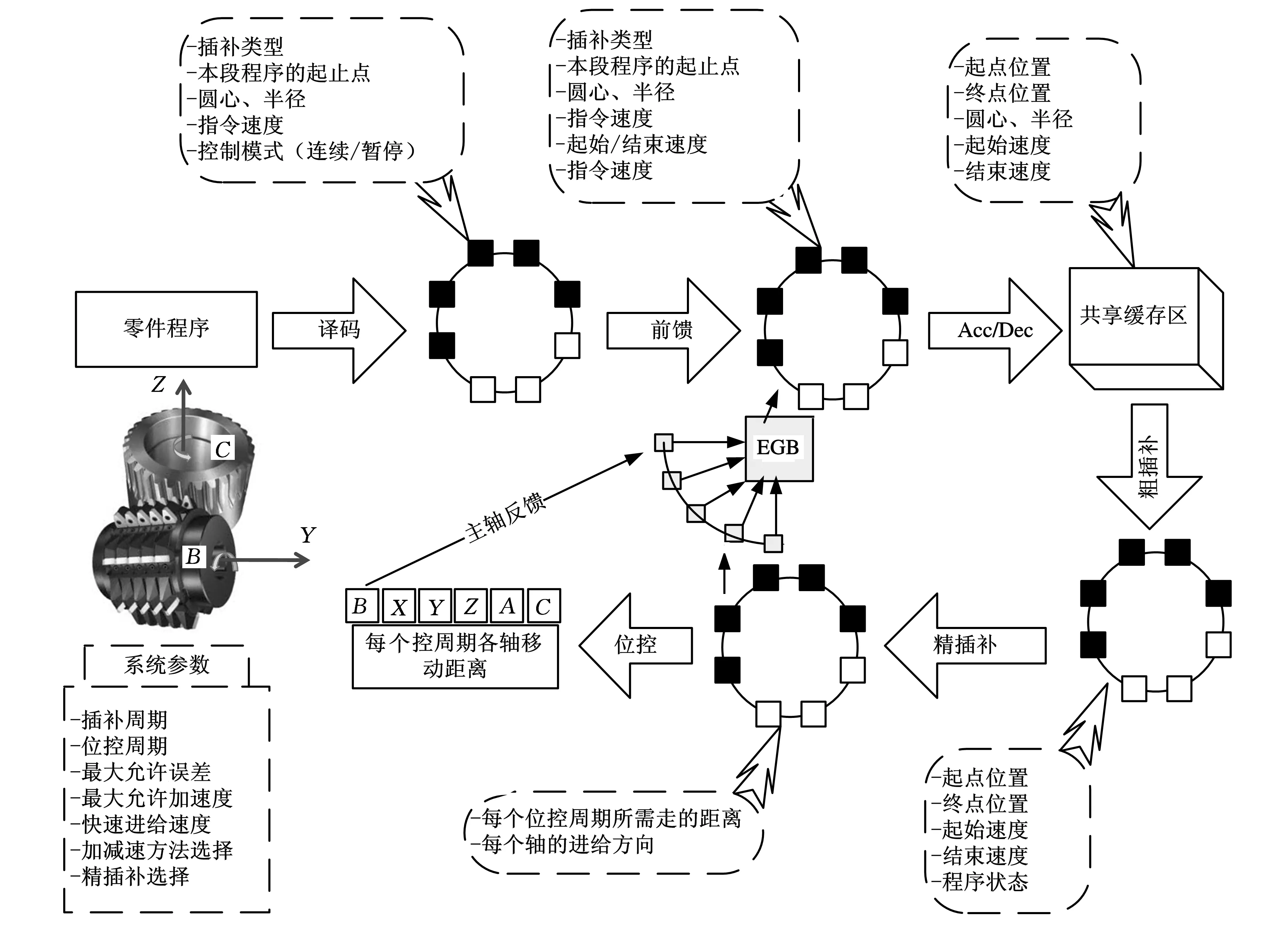
图2　电子齿轮箱的实现原理

2　电子齿轮箱控制误差分析

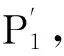
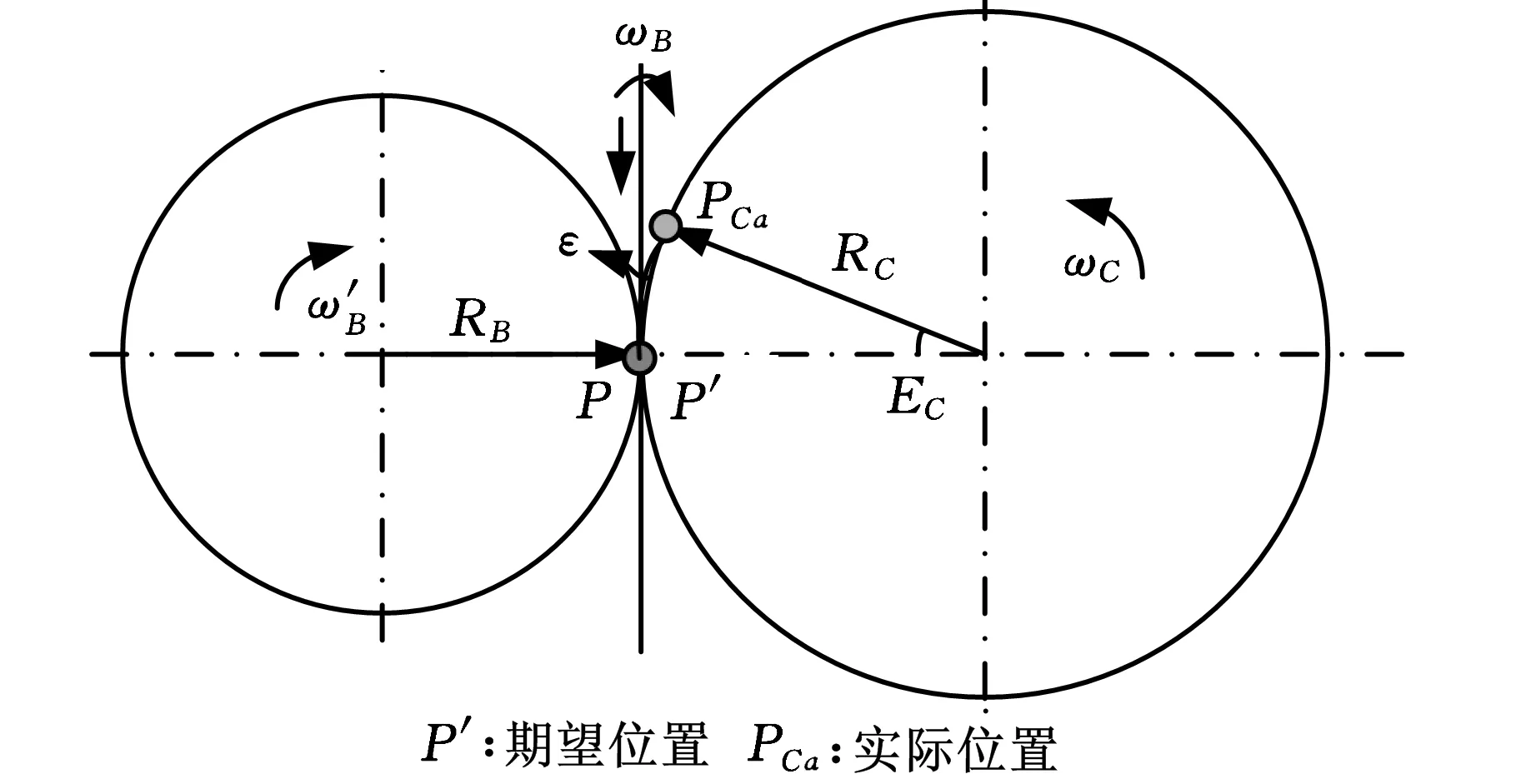
图3　电子齿轮箱误差的产生分析

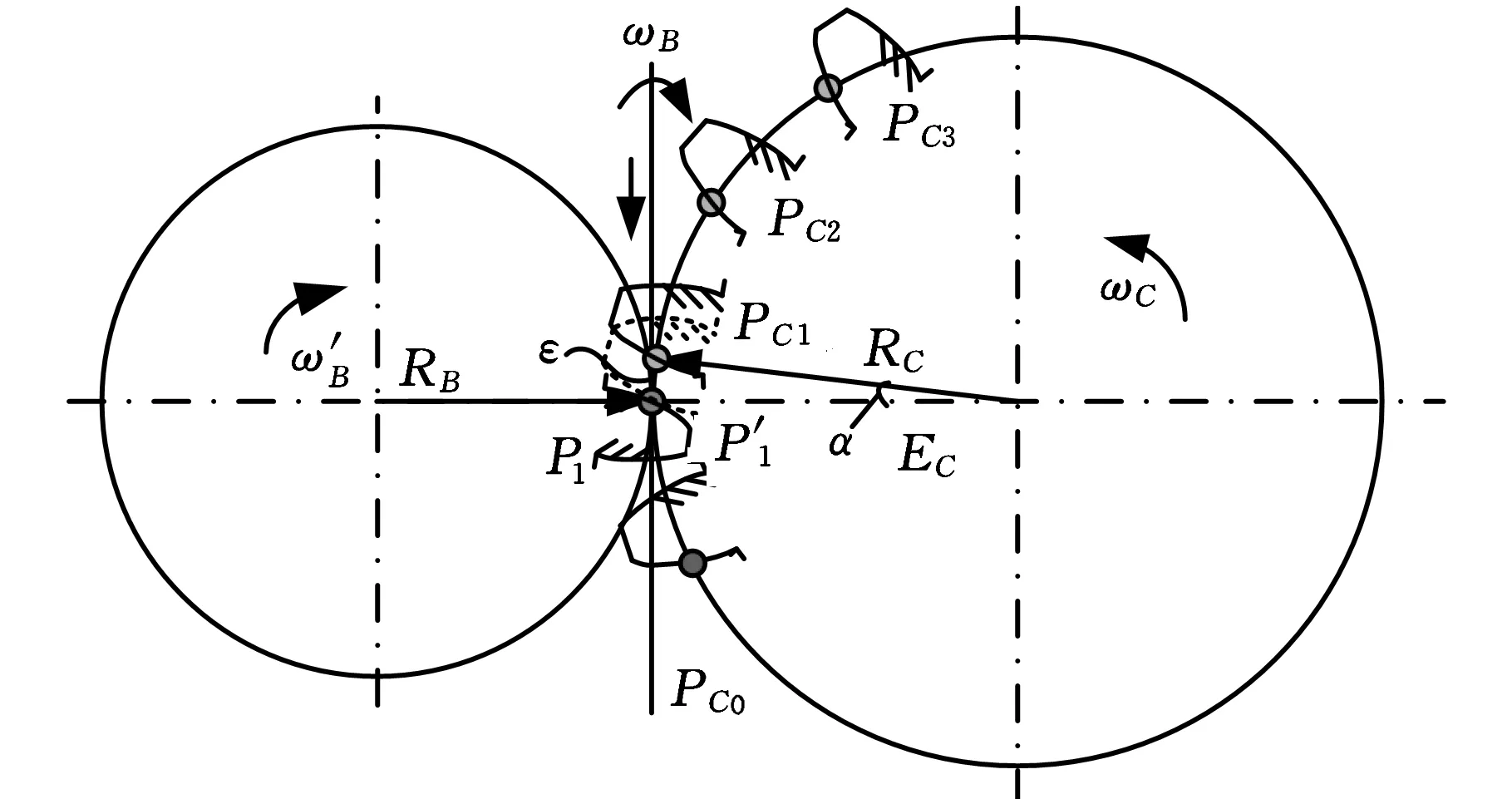
图4　电子齿轮箱误差的评价分析

设工件分度圆半径为RC,模数为m,齿数为ZC,则由几何关系得

fpt=RCα=ZCm α/2

(2)

其中,α为工件轴在此刻的角度跟随误差,而该误差在数控系统中可以实时计算得到,记为EC,故周节偏差可以表示为

fpt=ZCmEC/2

(3)

3　仿真研究

建立主从式电子齿轮箱控制模型,如图5所示,在没有Z轴方向的轴向切削和沿着Y向的窜刀运动时，C轴直接跟随B轴转动，设滚刀头数与工件齿数之比为1∶15,工件模数为6mm,则滚刀转速与工件转速之比为15∶1。由电子齿轮箱的控制误差分析可知，电子展成的精度主要决定于C轴本身的跟踪精度，因此若想提高电子齿轮箱的控制精度，则需提高C轴的跟随性能。本研究中增加了C轴的速度前馈和摩擦前馈，同时，C轴的转角误差补偿主要针对当滚刀有沿着Z轴的轴向移动或沿着Y轴的切向移动时，在插补环节根据式(1)计算得到的附加转动。

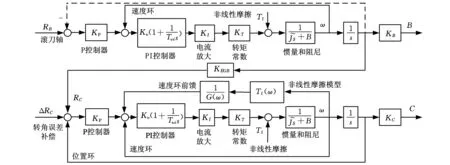
图5　电子齿轮箱仿真模型

本文采用的各轴参数见表1，其中系统参数的含义参见文献[14],首先,按照单轴最优的原则,分别对B轴、C轴进行阶跃响应测试，确定各轴的控制参数。根据系统的线性驱动模型，力矩到转速部分的传递函数为

(4)

式中,ω为电机角速度;Tm为电机产生的转矩,N·m;Td主要由系统运动过程中的非线性摩擦力矩Tf和机床加工产生的切削力矩Tc组成,N·m。

Tm与Td的差值用来驱动电机轴转动。因此,力矩到转矩的时域表达为

(5)

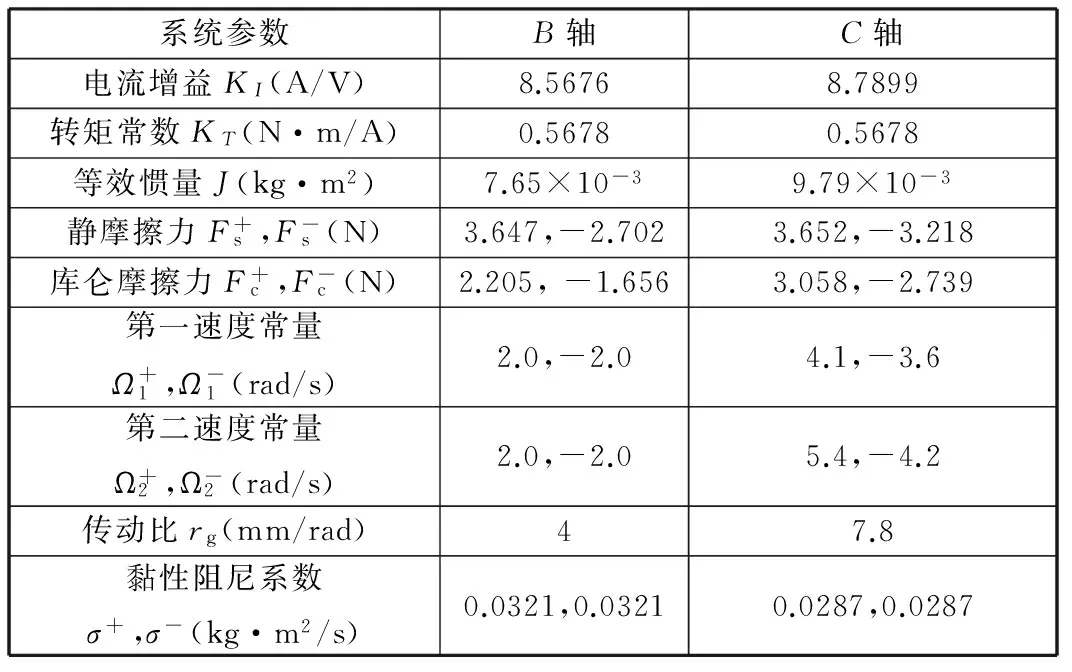
表1　电子齿轮箱仿真模型参数

注：上标“+”、“-”分别表示正向和负向。

Tm=B ω+Tf

(6)

由于Tm为电机输出转矩，与电枢电流成比例,B和Tf均为摩擦参数，故测得电机输出转矩和角速度,便可获得摩擦力。建立摩擦模型，根据运动轴在各转速下摩擦力的大小，可以辨识出影响摩擦力的各个参数，再根据测得的转速，估算出摩擦力的大小,在前馈中补偿掉。Tm的值由伺服驱动器输出,利用文献[14]对Lugre模型的近似方程，将式(6)写为

(7)

式(7)中的σ+和σ-相当于动态模型中的阻尼B。根据非线性摩擦模型估算出的非线性摩擦值，以前馈方式补偿到速度环的输入。

本文首先采用仿真的形式模拟电子齿轮箱控制轴(工件轴)对主动轴(滚刀轴)的跟随情况，其中，主轴的输入信号采用正弦变速信号。工件轴(C轴)对主轴(B轴)的跟踪情况如图6所示。无摩擦补偿情况下,电子齿轮箱控制下主从轴的跟踪误差分析如图7a所示,根据式(3)得到电子展成误差分析图(图7b)。根据式(7)，采用仿真形式对模型进行摩擦辨识和补偿，补偿后电子齿轮箱的跟踪性能如图8所示,C轴的跟随性能得到改善，电子展成的最大误差由2.0 μm减小为0.99 μm。

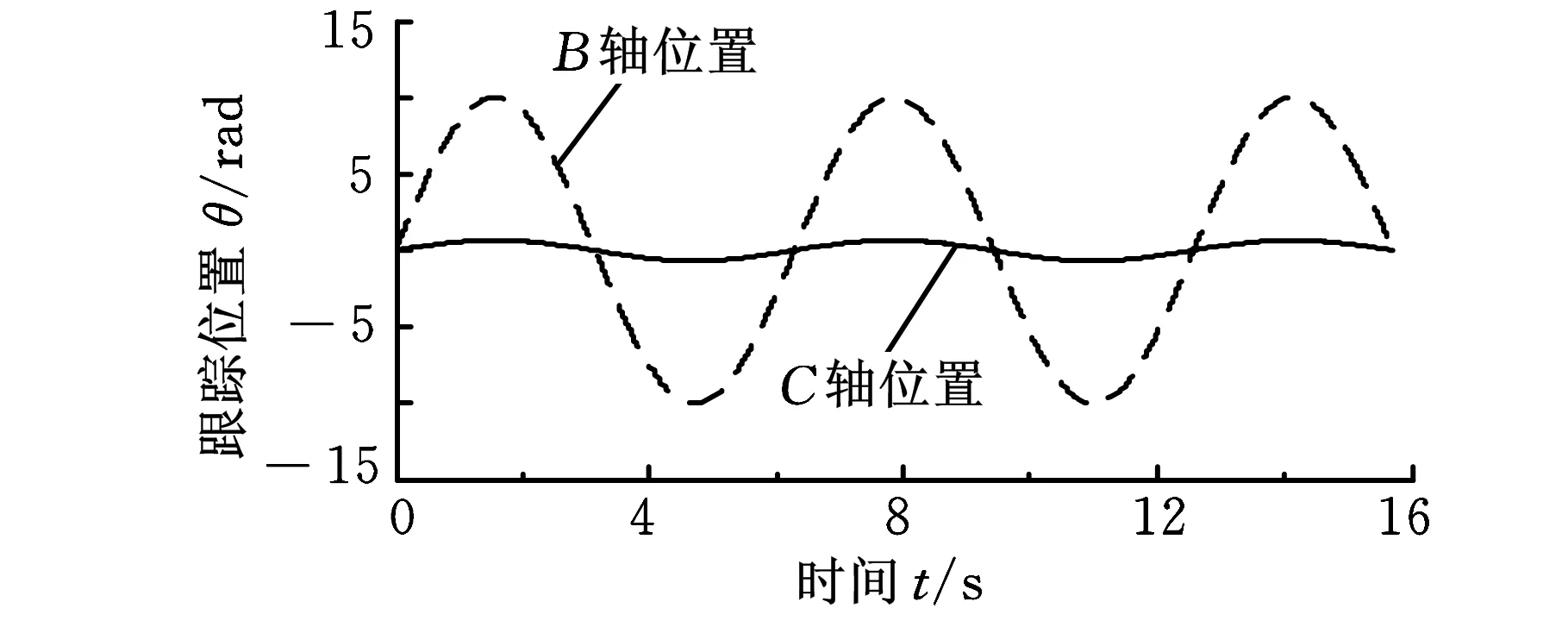
图6　电子齿轮箱跟踪性能仿真

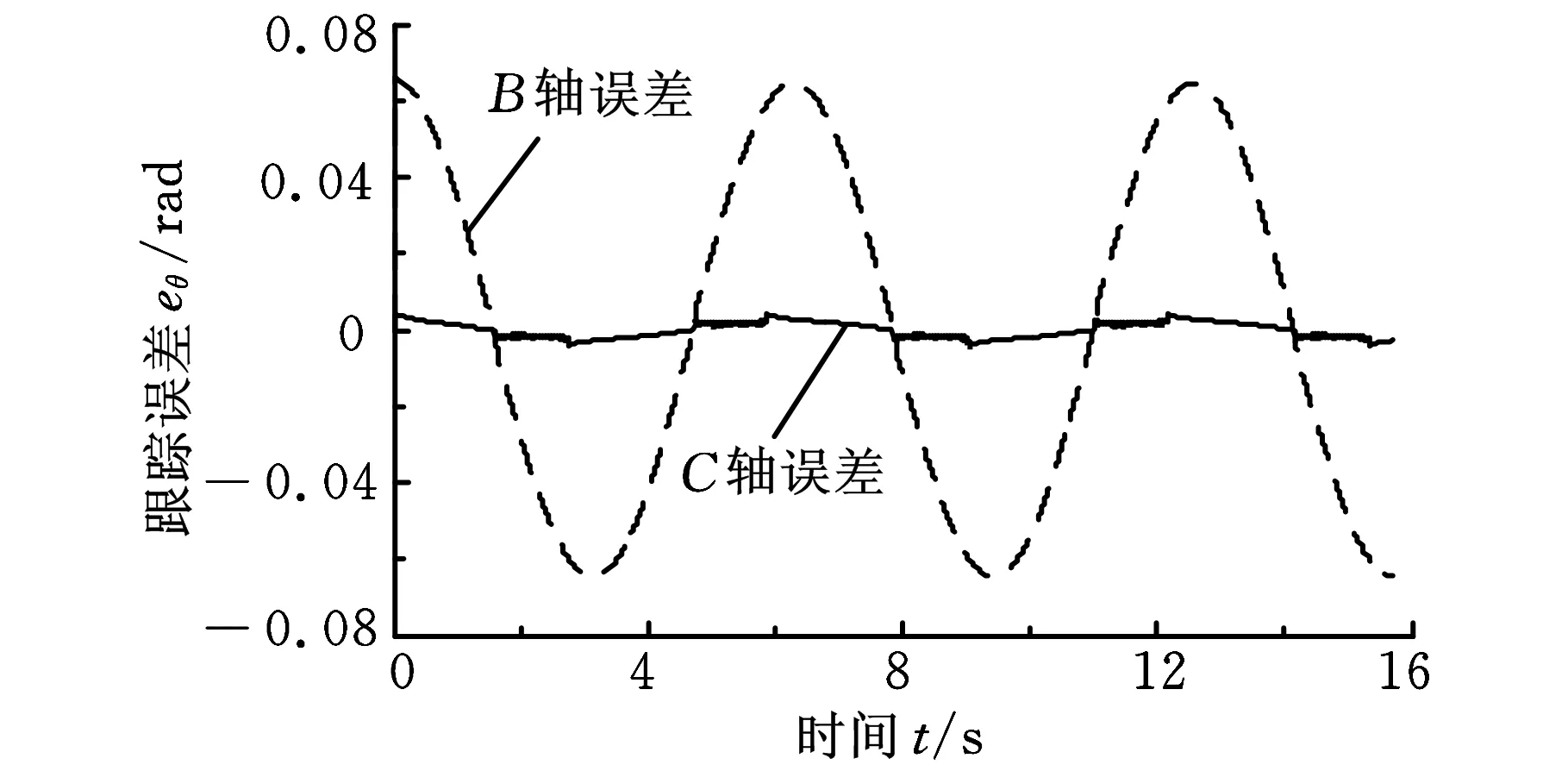
(a)跟踪误差

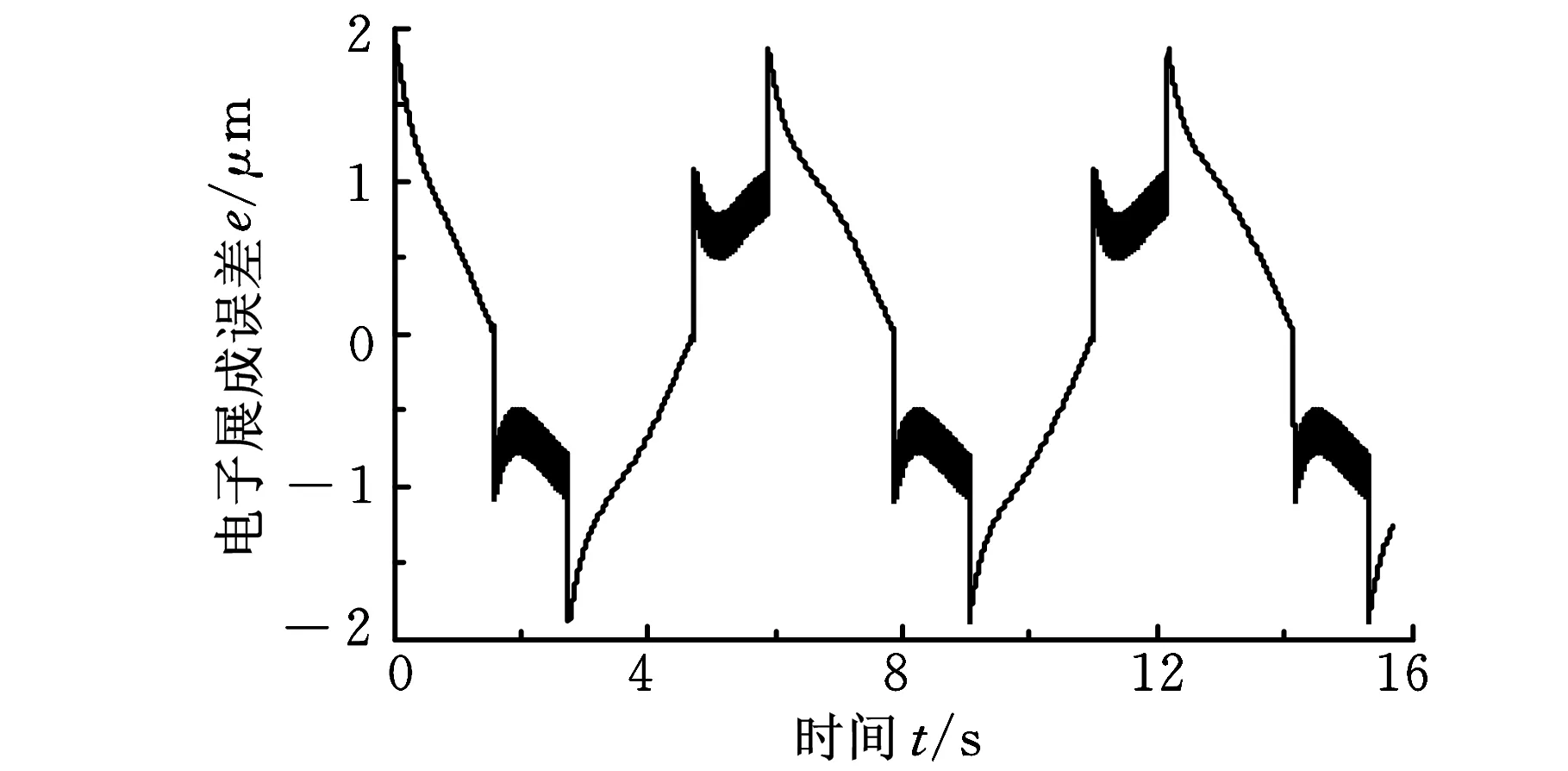
(b)电子展成误差图7　补偿前的电子齿轮箱跟踪性能分析

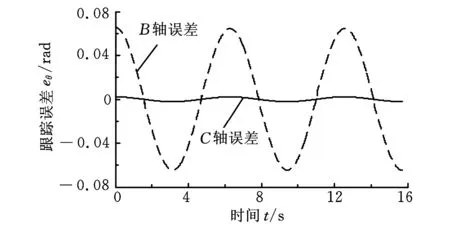
(a)跟踪误差

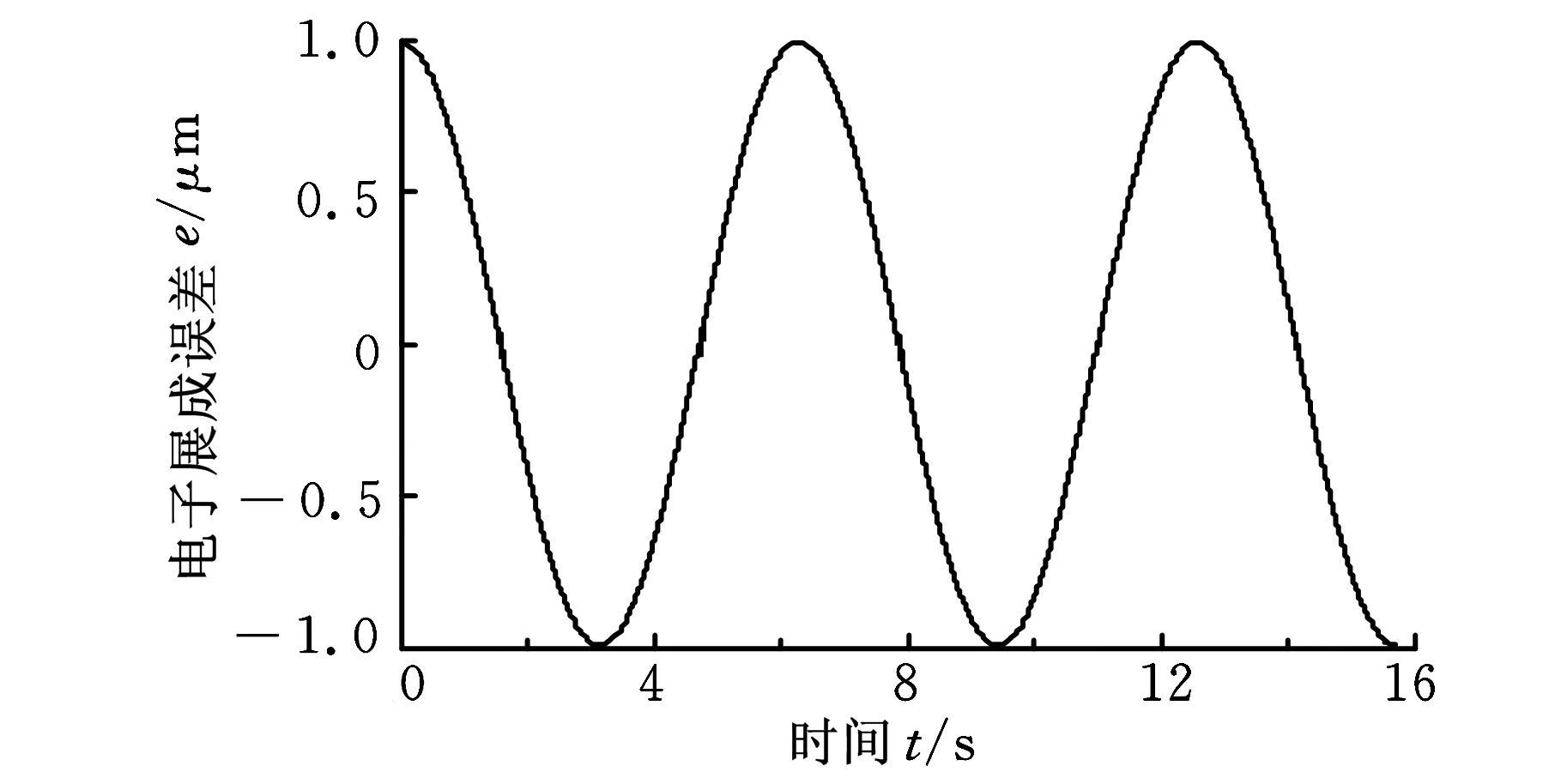
(b)电子展成误差图8　补偿后的电子齿轮箱跟踪性能分析

4　实验研究

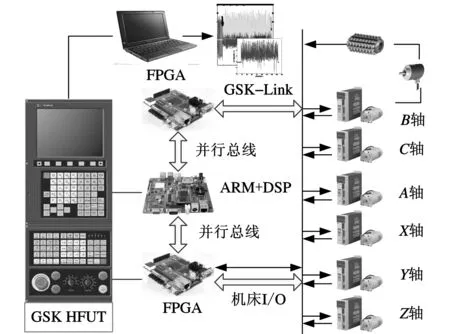
图9　六轴滚齿数控系统

自主研发的带电子齿轮箱功能的六轴数控滚齿系统如图9所示。该平台的控制结构与上一节仿真实验的控制结构相同，即采用P-PI控制方式，其中位置环在数控系统中实现，速度环在伺服驱动中实现。数控系统在运动过程中实时记录每个控制周期的各轴指令位置和反馈位置，并传给上位机电脑,然后在MATLAB中计算分析各轴运动情况。

实验采用轴向滚切法加工斜齿轮,工件参数和刀具参数如表2所示,主轴转速为200 r/min,径向和轴向的切削速度均为100 mm/min。

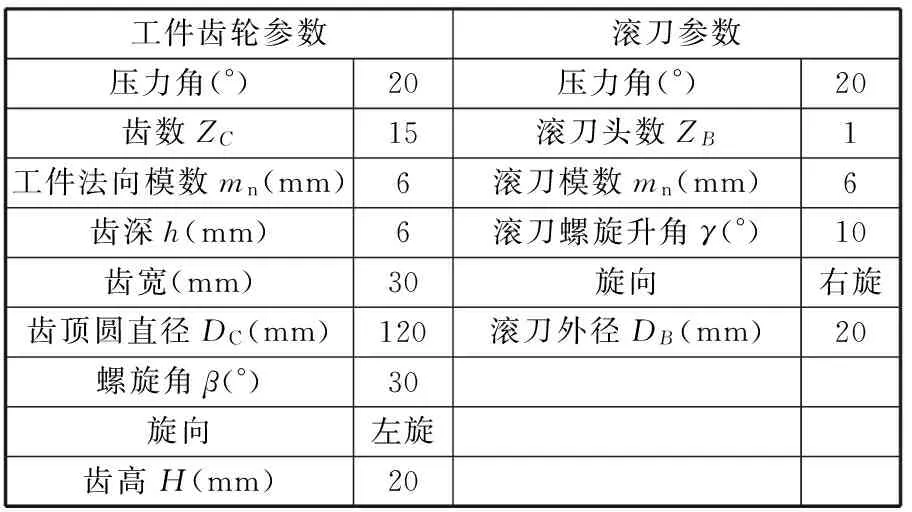
表2　实验所采用的工件与滚刀参数

运动过程中,工件轴依据式(1)跟随刀具轴运动,电子齿轮箱的展成误差分析如图10所示,其中电子齿轮箱展成误差的最大值为7.9 μm,平均值为2.5 μm,均方根值为3.1 μm。

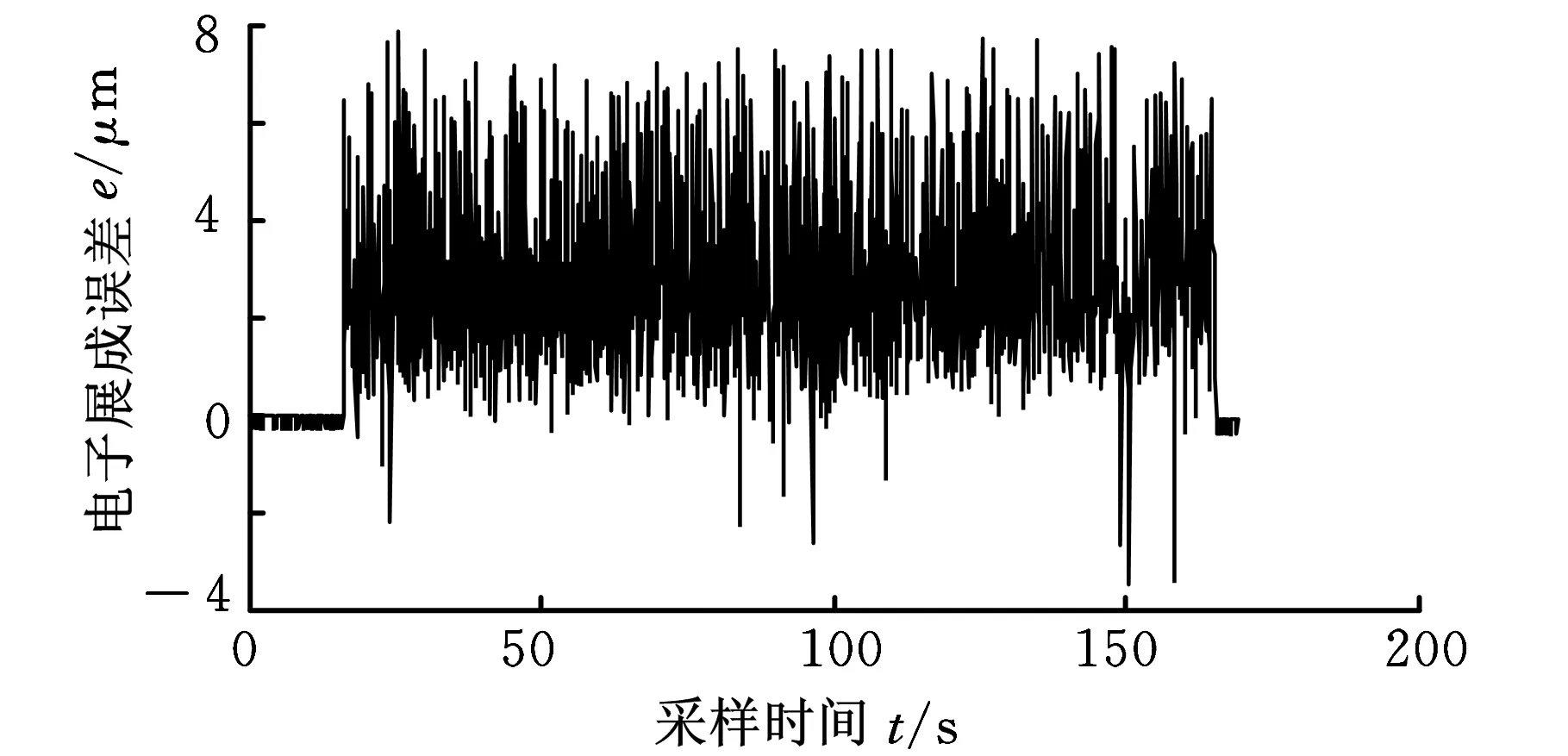
图10　电子齿轮箱展成误差分析

5　加工实例

齿轮的加工实验设备为重庆机床厂的YS3118数控滚齿机以及自主研发的带电子齿轮箱的数控系统GSK-HFUT 25iG。加工工件直齿轮参数如下:齿数Z为42,模数为3 mm,压力角为20°,分度圆直径为126 mm,齿顶圆直径为132 mm,齿宽为40 mm,材料为45钢,热处理条件为T170～215。刀具参数如下:头数为1,模数为3 mm,螺旋升角(右旋)为2°24′。工艺参数如下:采用3次轴向滚切加工法,第一刀和第二刀的进给量均为3 mm,第三刀的进给量为0.5 mm。

经哈尔滨量具刃具集团有限责任公司的3096型齿轮测量中心检测,齿距累计总偏差如图11所示,最大值为14.9 μm(4级精度)。单个齿距偏差如图12所示,最大值为5.7 μm(5级精度),均满足加工要求,达到较高精度。

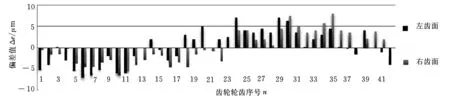
图11　齿距累计总偏差测量结果

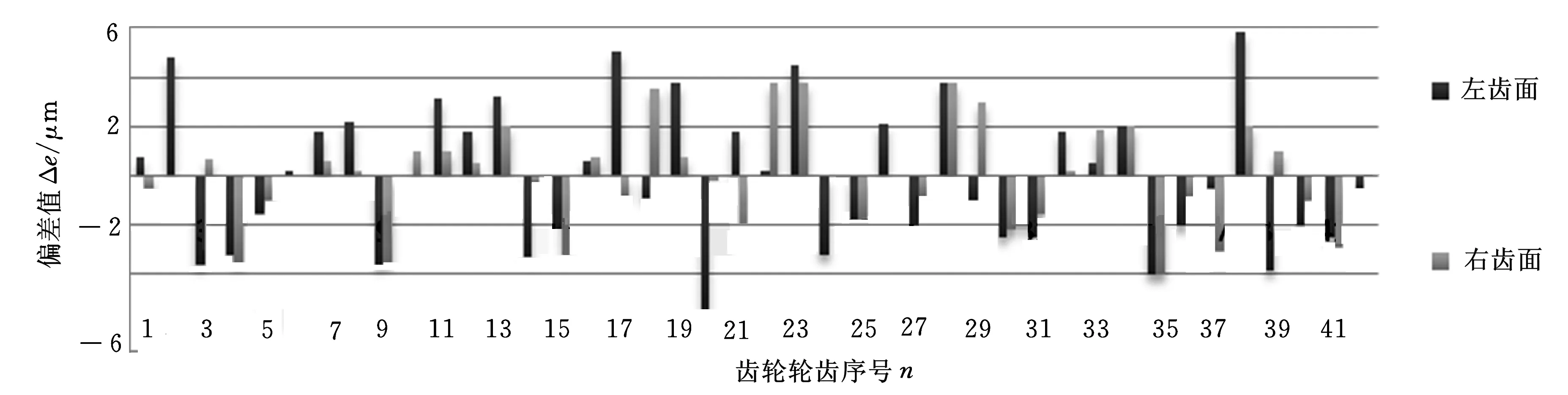
图12　单个齿距偏差测量结果

6　结论

(1)采用软件式电子齿轮箱提高了齿轮加工数控系统的柔性，即电子齿轮箱的展成误差是可控、可预测的。

(2)通过摩擦补偿提高了跟随轴的跟踪误差，可以直接减小电子齿轮箱的展成误差。

(3)将自主研发带电子齿轮箱的数控系统应用于YS3118数控滚齿机后，所加工的齿轮试件齿距累计总偏差最大值为14.9 μm，单个齿距偏差最大值为5.7 μm,均满足加工要求，具有较高精度。

[1]权建洲,谭伟明,殷红彦.软件电子齿轮箱实现方法研究[J].机电一体化,1999(3):20-22.

Quan Jianzhou,Tan Weiming,Yin Hongyan. Research on Realizing Method of Electronic Gearbox with Computer Software[J]. Mechatronics,1999(3):20-22.

[2]庄磊. 电子齿轮箱关键控制技术及其应用研究[D]. 南京：南京航空航天大学，2001.

[3]庄磊，左敦稳，王珉. 基于电子齿轮箱传动的多边形截面零件车削[J]. 机械设计与制造，2001(2):76-77.

Zhuang Lei,Zuo Dunwen,Wang Min.Polygonal Cross-section Parts Turning Based on the Electronic Gear-box[J].Machine Design and Manufacturing,2001(2):76-77.

[4]庄磊,左敦稳,王珉,等.电子齿轮箱系统的研究与应用[J].机械设计与制造工程,2001(2):48-50.

Zhuang Lei,Zuo Dunwen,Wang Min,et al.Research and Application of Electronic Gear-box[J].Machine Design and Manufacturing Engineering,2001(2):48-50.

[5]李炽岚,熊显文.斜齿轮全数字化插齿加工运动控制方法研究[J].机械传动,2007(5):30-33.

Li Chilan,Xiong Xianwen.Study on Processing Movement Controlling Method of Helical Gear Entire Digitization Slot[J].Journal of Mechanical Transmission,2007(5):30-33.

[6]张新玉，张根保，黄强，等. 零传动滚齿机传动链精度分析[J]. 制造技术与机床，2007(10)：59-61.

Zhang Xinyu，Zhang Genbao，Huang Qiang，et al. Analysis on Transmission Error of Direct-driving Hobbing Machine[J]. Manufacturing Technology & Machine Tool，2007(10)：59-61.

[7]曹东锋，张根保，黄强，等. 零传动滚齿机内联传动技术研究及实现[J]. 机械设计与制造，2008(5):216-218.

Cao Dongfeng,Zhang Genbao,Huang Qiang,et al.Research on the Inner-link Transmission Technique of Direct-drive Gear Hobbing Machine and Its Realisation[J].Machinery Design & Manufacture,2008(5):216-218.

[8]胡赤兵，田芳勇，姜衍仓. 电子齿轮箱在非圆齿轮滚齿加工中的应用[J]. 机械设计与制造，2009(12)：79-81.

Hu Chibing,Tian Fangyong,Jiang Yancang.Application of the Electrical Gearbox in the Hobbing Non-circular Gear[J]. Machinery Design & Manufacture，2009(12)：79-81.

[9]黄强，张根保，刘润爱. 零传动提高滚齿机展成运动精度的作用机理[J]. 中国机械工程，2009，20(4): 379-382.

Huang Qiang，Zhang Genbao，Liu Runai. On Action Mechanism of Improving Generating Motion Accuracy on Hobber with Zero Transmission[J]. China Mechanical Engineering,2009,20(4):379-382.

[10]Bai B.Computerized Tooth Profile Generation of Elliptical Gears Manufactured by Shaper Cutters[J].Journal of Materials Processing Technology,2002,122(2/3):139-147.

[11]Bouzakis K D，Lili E，Michailidis N，et al. Manufacturing of Cylindrical Gears by Generating Cutting Processes:A Critical Synthesis of Analysis Methods[J]. CIRP Annals-manufacturing Technology，2008，57(2)：676-696.

[12]Litvin F L,Gonzalez-Perez I,Fuentes A,et al.Topology of Modified Surfaces of Involute Helical Gears with Line Contact Developed for Improvement of Bearing Contact,Reduction of Transmission Errors,and Stress Analysis[J].Mathematical and Computer Modelling,2005,42(9/10):1063-1078.

[13]Suh S,Kang S,Chung D,et al.Theory and Design of CNC Systems[M].London:Springer,2008.

[14]Erkorkmaz K,Altintas Y.High Speed CNC System Design.Part Ⅱ:Modeling and Identification of Feed Drives[J]. International Journal of Machine Tools & Manufacture,2001,41(10):1487-1509.

(编辑张洋)

Precision Control and Experiments of Electronic Gearbox

Tian Xiaoqing Han JiangXia Lian

Hefei University of Technology,Hefei,230009

The implementation principles of EGB and the EGB realization method in CNC system were first studied herein.Then,the reasons of gear generating errors were discussed from the point of geometric view,and the instantaneous EGB control error calculation formula was deduced. In addition, the simulation models of EGB were built, the control errors were obtained by simulation analysis and optimization,and the optimization model was applied into the CNC system of six axis experimental platform.Then,the errors were analyzed under the no-load conditions.Finally,the CNC system with EGB was applied in YS3118 CNC gear hobbing machine.The gear machining and measuring results show that the EGB control precision can satisfy the demands of gear machining.

electronic gearbox(EGB);gear-hobbing;generating;feedforward

2013-09-12

国家科技支撑计划资助项目(2012BAF13B01)

TP273< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.02.015

田晓青,女,1987年生。合肥工业大学机械与汽车工程学院博士研究生。主要研究方向为数控技术与数控装备。发表论文10篇。韩江,男,1963年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。夏链,女,1964年生。合肥工业大学机械与汽车工程学院教授。