考虑平均应力效应的Tovo-Benasciutti疲劳寿命预测模型

程军圣　袁　毅　喻镇涛　袁　辉

1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100822.东风汽车公司，襄阳，441004

考虑平均应力效应的Tovo-Benasciutti疲劳寿命预测模型

程军圣1袁毅1喻镇涛2袁辉2

1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100822.东风汽车公司，襄阳，441004

为了考虑平均应力对循环载荷作用下结构振动疲劳寿命的影响，对Tovo-Benasciutti疲劳损伤模型进行了平均应力修正。采用径向基函数法构造平均应力修正系数与随机应力带宽系数之间的近似模型,建立了考虑平均应力的Tovo-Benasciutti疲劳损伤模型。利用所建立的模型对某简单梁进行了疲劳寿命估计。结果表明：考虑平均应力效应的Tovo-Benasciutti模型能得到与试验更一致的结果。

平均应力；径向基函数；近似模型；振动疲劳；疲劳寿命预测

0　引言

结构振动疲劳是指结构所受动态交变载荷的频率分布与结构固有频率分布具有交集或相接近时，结构共振所导致的疲劳破坏现象[1]。目前，研究和应用较多的是以功率谱密度为基础的频域疲劳寿命预测法，此类方法有一个共同的特点，即都只考虑了随机应力的幅值影响，而忽略了平均应力的影响。实际上，结构的疲劳损伤不仅与随机应力的幅值和频率范围相关，而且与平均应力有关。平均应力大于零时表示拉伸平均应力，对疲劳有不利的影响；反之，对疲劳的影响是有利的[2]。为了考虑平均应力效应对高周疲劳强度的影响，Gerber、Goodman、High和Soderberg等分别提出了完全基于经验的早期模型[3]。在这些早期模型中，Goodman模型简单且最具有吸引力，特别是在疲劳极限时，对处理平均拉应力非常有效。但是，这些早期模型都只应用在时域疲劳寿命估计中，即对经雨流计数之后的随机应力循环进行平均应力修正，而在以功率谱为基础的频域疲劳寿命估计中却并未对平均应力进行修正。

按照频域法解决疲劳寿命估计的思路，研究考虑平均应力效应的疲劳损伤模型需要构造雨流幅值和均值的联合概率密度函数，并且需要将应力幅值修正为等效应力幅值。由于随机应力过程雨流幅值和均值相关性很小[4]，可假设随机应力的雨流幅值和均值是相互独立的，即雨流幅值和均值的联合概率密度表示为两者的乘积。等效应力幅值可采用经典的Goodman模型[5]进行平均应力修正而得到。基于以上两点，可以用一个平均应力修正系数表示考虑平均应力效应与未考虑平均应力效应的疲劳损伤之间的关系。该平均应力修正系数仅与雨流均值的概率密度函数和材料极限强度有关。因此，针对某种具体材料，可以建立平均应力修正系数与带宽系数之间的近似函数。

径向函数是指以待测点与样本点之间的欧氏距离为自变量的一种函数，而径向基函数模型是以径向函数为基函数，通过线性叠加构造出的近似模型[6]，并且径向基函数模型在很多领域都有广泛的应用[7]。本文对5种不同功率谱几何形状、不同带宽系数的随机应力进行了仿真，构造出平均应力修正系数的径向基函数模型。一方面，从频域出发，利用Tovo-Benasciutti模型得到不考虑平均应力的疲劳损伤；另一方面，从时域出发，经雨流计数和Miner累计损伤，并结合Goodman平均应力修正，得到考虑平均应力的疲劳损伤。然后，对4000组样本进行训练，得到了一种关于平均应力修正系数和带宽系数的径向基函数模型，并对平均应力修正系数的径向基函数模型进行了仿真验证，发现平均应力修正系数的径向基函数模型误差绝大多数控制在10%以内。最后，利用考虑平均应力的Tovo-Benasciutti疲劳损伤模型对某简单梁进行了疲劳寿命估计。

1　考虑平均应力效应的Tovo-Benasciutti疲劳损伤模型

只考虑随机应力雨流幅值概率密度的疲劳损伤模型为

(1)

式中，D(t)为时间t内只考虑幅值影响的总疲劳损伤量；E[P]为随机应力峰值穿越频率；A、m为材料参数；P(S)为雨流幅值概率密度；S为应力幅值；T为应力循环总时间。

考虑平均应力效应的疲劳损伤模型为

(2)

式中，D′(t)为时间t内考虑平均应力效应的总疲劳损伤量；P(S,Sm)为随机应力雨流幅值和雨流均值的联合概率密度函数；n(t)为任意幅值和均值应力的循环次数；NT(S,Sm)为任意幅值和均值应力的失效循环次数。

文献[4]的研究结果表明，随机应力的雨流幅值和雨流均值相关性很小。假设它们是相互独立的，则P(S,Sm)可表示为

P(S,Sm)=P(S)P(Sm)

(3)

使用Goodman模型进行平均应力修正[7]：

(4)

式中，Seq为等效应力幅值；Sb为抗拉强度。

同时考虑随机应力雨流幅值和雨流均值的疲劳损伤模型可以表示为

(5)

从式(5)可以看出：若要得到同时考虑幅值效应和平均应力效应的疲劳损伤寿命，除了要知道幅值概率密度函数模型以外，还要知道均值概率密度函数模型，然而现有的频域振动疲劳模型对幅值概率函数模型研究较多，但对均值概率密度函数模型研究较少。因此，本文借鉴早期解决宽带随机过程下疲劳损伤模型时对窄带随机过程进行近似处理的思路，对只考虑幅值影响的振动疲劳损伤模型进行近似处理，得到同时考虑幅值和均值效应的疲劳损伤模型。

式(5)可以进一步表示为

其中平均应力修正系数λm为

(6)

假设只考虑幅值影响的振动疲劳损伤模型采用Tovo-Benasciutti模型[8]，则同时考虑幅值效应和平均应力效应的Tovo-Benasciutti疲劳损伤模型可表示为

(7)

b=(α1-α2)[1.112(1+α1α2-α1-α2)·

e2.11α2+α1-α2]/(α2-1)2

由式(6)可以看出，考虑平均应力效应的Tovo-Benasciutti模型中，平均应力修正系数只与雨流均值的概率密度函数和材料极限强度有关。因此，针对某种具体材料，可以建立平均应力修正系数与带宽系数之间的近似函数。

2　关于平均应力修正系数的径向基函数模型

根据逼近函数形式的不同，近似模型的构建方法可以分为多种。目前工程中应用较多的主要有人工神经网络模型、Kriging函数模型、径向基函数模型和多项式响应面模型等。有研究表明，径向基函数法与传统的统计学全局优化方法有较好的一致性。因此，可以用径向基函数法建立平均应力修正系数模型。

为了得到一种比较精确的径向基函数模型，需要对多组样本进行训练。参考Tovo-Benasciutti模型中对系数b模型的构造方法，对5种不同功率谱几何形状、不同带宽系数的单边功率谱进行仿真。其中，5种不同单边功率谱几何形状如图1所示。

(a) (b)(c)

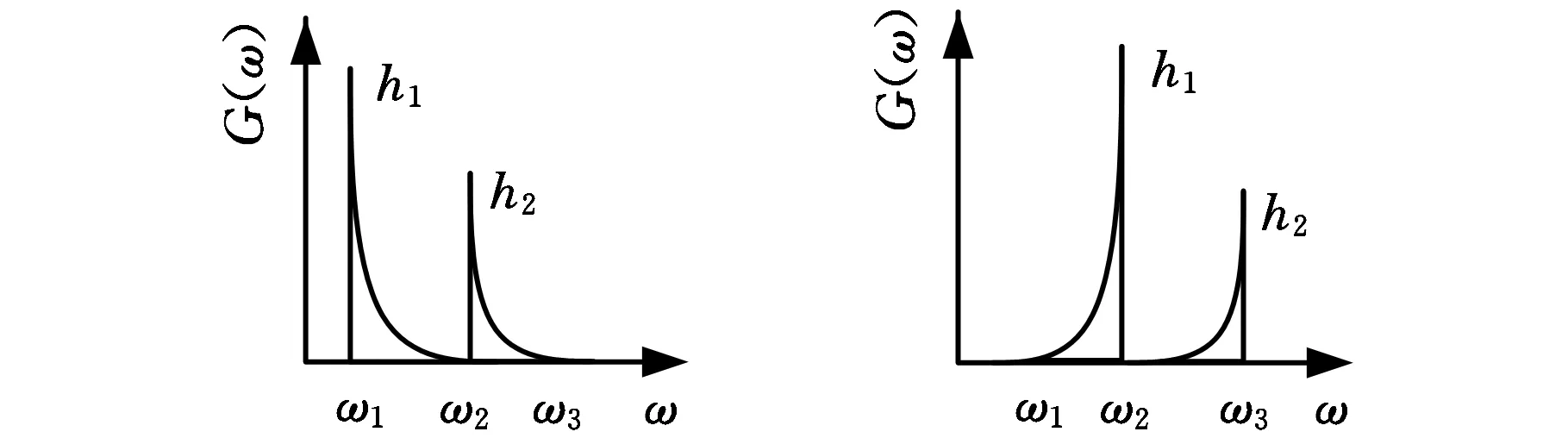
(e)(f)图1　5种不同的单边功率谱几何形状

若单边功率谱的频率ω1、ω2、ω3已确定，则带宽系数(α1,α2)由应力功率谱的幅值(h1,h2)唯一决定。根据试验设计方法合理选择了4000组不同的(h1,h2)样本对，每组(h1,h2)对应一组(α1,α2)。针对每组(h1,h2)确定的单边功率谱，一方面，从频域出发，用Tovo-Benasciutti模型得到不考虑平均应力的疲劳损伤；另一方面，从时域出发，经雨流计数和Miner累计损伤，并结合Goodman模型平均应力修正，得到考虑平均应力的疲劳损伤。于是得到每个样本对(h1,h2)或(α1,α2)下的平均应力修正系数λm。4000组不同样本的α1、α2、λm变化情况如图2所示。对4000组样本进行训练，得到径向基函数模型，并对1000组不同样本(α1,α2)进行验证，相对误差如图3所示，绝大多数误差都控制在10%以内，结果表明：径向基函数模型可以比较精确地表示平均应力修正系数。

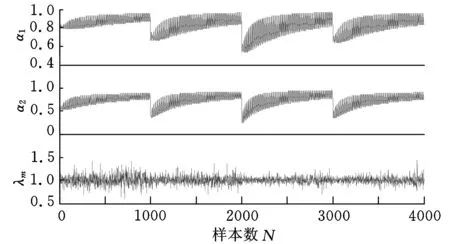
图2　4000组不同样本的α1、α2、λm变化情况

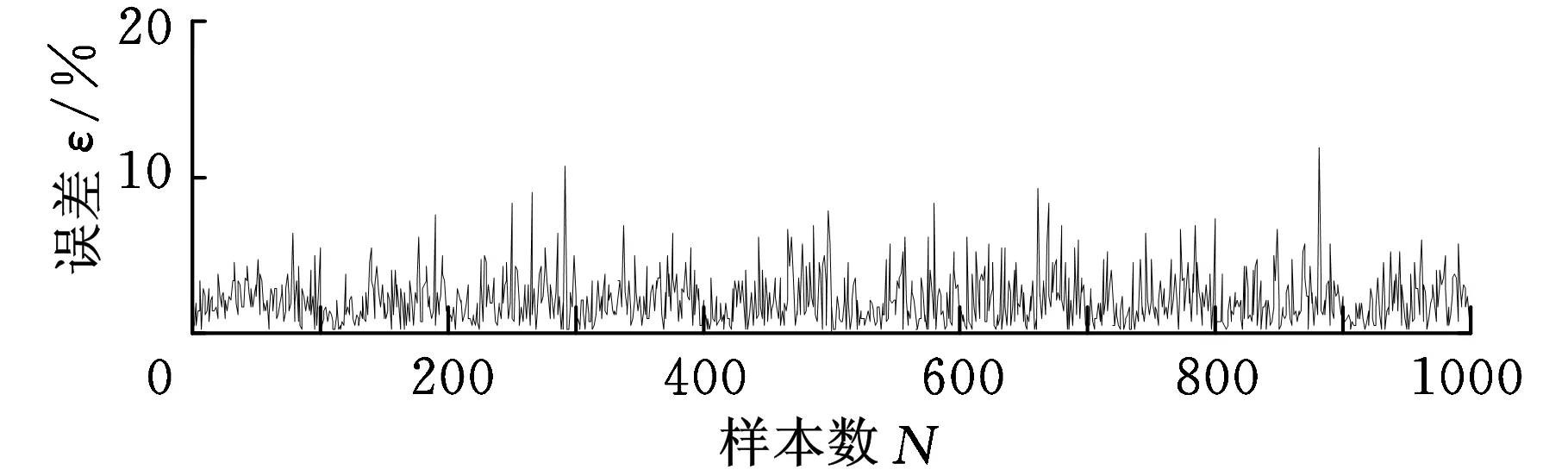
图3　1000组样本误差曲线

3　考虑平均应力效应的Tovo-Benasciutti疲劳损伤模型的应用

本文参考王明珠[9]提出的试验模型进行仿真分析，并对结果进行对比分析。试验件的材料为LY12CZ铝合金，取自厚度为6mm的板材。LY12CZ铝合金材料室温下的常规机械性能见表1。

表1　LY12CZ铝合金机械性能

试验件为圆形槽缺口试件，试验件具体形状和尺寸如图4所示。

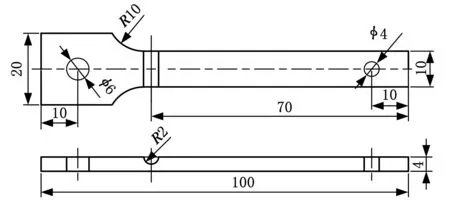
图4　试验件结构示意图

为了改变LY12CZ铝合金悬臂梁结构的固有频率和响应结果，在试件右端圆孔处加载配重块，上下各3块，配重块的材料为A3钢，几何尺寸如图5所示。

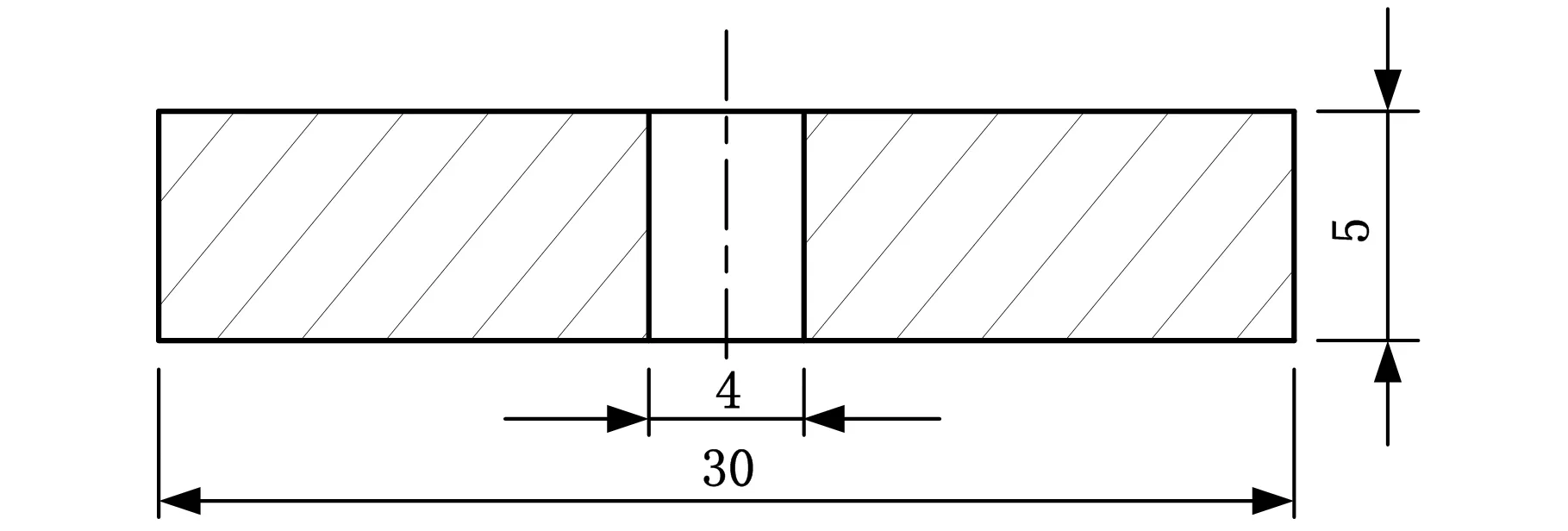
图5　配重块结构示意图

振动疲劳试验采用基础振动的加载方式，输入载荷为加速度功率谱密度，具体如图6、图7所示。试件通过左端孔固定在模具上，呈悬臂梁结构。

图6　圆形槽试验件

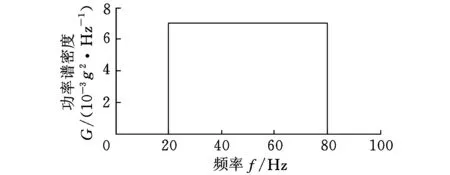
(a)BⅠ激励谱

(b)BⅡ激励谱图7　激励谱

比较现有的不同方法求出的疲劳寿命[9]见表2。

表2　不同方法计算结果的比较　min

窄带法、WL修正法和G修正法都属于幅值分布法中的窄带法，把雨流幅值分布非常复杂的宽带高斯过程通过窄带近似、甚至直接通过窄带法计算，必然造成较大的误差。Dirlik模型和Tovo-Benasciutti模型属于幅值分布法的宽带法，直接给出了宽带雨流幅值分布模型，但由于模型本身没有将平均应力的影响考虑在内，结果误差也较大，并且Dirlik模型还没有任何一个理论解释作为支撑。而本文提出的考虑平均应力效应的Tovo-Benasciutti模型考虑了平均应力的影响，所以可以得到与试验更一致的结果。但是，仍与试验结果有很大的误差，一方面原因是试验的偶然因素，另一方面原因是结构振动疲劳寿命预测的复杂性，如材料应力-寿命曲线的准确性等。

4　结语

本文在假设随机应力雨流幅值和雨流均值概率密度相互独立的前提下，认为平均应力效应对疲劳损伤的影响可以用一个平均应力修正系数表示，并且该平均应力修正系数只与雨流幅值概率密度和材料极限强度有关。提出利用径向基函数法建立平均应力修正系数与带宽系数之间的关系，建立了考虑平均应力效应的Tovo-Benasciutti疲劳损伤模型，对某简单梁进行对比验证。结果表明：本文提出的考虑平均应力效应的Tovo-Benasciutti模型可以得到与试验更一致的结果。

[1]高清振，王耀华，张晓南.基于样本法的某型飞机救生机构振动疲劳寿命估算[J].中国机械工程,2011，22(2):162-165.

Gao Qingzhen,Wang Yaohua,Zhang Xiaonan.Fatigue Life Prediction of Aeronautic Rescue Mechanism under Random Vibration Based on Sample Approch[J]. China Mechanical Engineering,2011,22(2):162-165.

[2]王国军.Msc.Fatigue疲劳分析实例指导教程[M].北京：机械工业出版社，2009.

[3]张然治.疲劳试验测试分析理论与实践[M].北京：国防工业出版社，2011.

[4]Wang Xiangyu. Random Fatigue of Structural with Uncertain Parameters and Non-Gaussian Stress Response[D]. Delaware:University of Delaware,2004.

[5]Smith K N, Watson P, Topper T H. A Stress-strain Function for Fatigue of Metals[J]. Journal of Material, 1970,5(4):767-778.

[6]聂祚兴.车身噪声传递函数的全局灵敏度分析及稳健优化设计[D]. 长沙：湖南大学，2012.

[7]Gutmann H M. A Radial Basis Function Method for Global Optimization[J].Journal of Global Optimization, 2001,19:201-227.

[8]Benasciutti D, Tovo R.Cycle Distribution and Fatigue Damage Assessment in Broad-band Non-Gaussian Random Process[J]. Probabilistic Engineering Mechanics, 2005,20:115-127.

[9]王明珠.结构振动疲劳寿命分析方法研究[D]. 南京：南京航空航天大学，2009.

(编辑陈勇)

Predicative Methods of Tovo-Benasciutti Fatigue Life under Considering Mean Stress Effects

Cheng Junsheng1Yuan Yi1Yu Zhentao2Yuan Hui2

1.State key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University,Changsha,410082 2.Dongfeng Motor Corporation,Xiangyang,Hubei,441004

In order to consider the mean stress effects on the structural vibration fatigue life under cyclic loads,the paper proposed a method to revise the Tovo-Benasciutti fatigue damage model. An approximate model between the mean stress correcting coefficient and the random stress band coefficient was built with radial basis function, and the Tovo-Benasciutti fatigue damage model was built under considering the mean stress effects. The fatigue life for a simple beam was estimated with Tovo-Benasciutti fatigue damage model under considering the mean stress effects, the results show that the Tovo-Benasciutti fatigue damage model under considering the mean stress effects can get a closer result to the test.

mean stress; radial basis function; approximate model; vibration fatigue; fatigue life prediction

2013-09-02

V215.5DOI：10.3969/j.issn.1004-132X.2015.02.012

程军圣，男，1968年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。主要研究方向为动态信号分析与处理、机电设备状态监测与故障诊断、振动与噪声控制。袁毅，男，1988年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。喻镇涛，男，1988年生。东风汽车公司技术中心试验部工程师。袁辉，男，1988年生。东风汽车公司技术中心试验部工程师。