逆向物流网络设计多目标随机规划模型

张群　卫李蓉

摘要：以钢铁工业企业废钢回收循环利用为背景，对企业的逆向物流网络进行设计。考虑需求市场需求量、废钢回收量以及回收产品质量的不确定性，以物流网络成本以及对环境的影响最小化为目标，建立了多目标随机规划模型，决策逆向物流网络中工厂以及回收处理中心的位置、数目和网络节点间的物流量分配。利用约束法处理多目标转化为单目标模型，结合情景分析对随机规划模型进行求解。最后，在MATLAB2014a平台调用CPLEX，用算例验证了模型的有效性，并对ε参数的敏感性进行了分析。

关键词：逆向物流；网络设计；随机规划；多目标规划

DOI：10.13956/j.ss.1001-8409.2015.10.26

中图分类号：F252文献标识码：A 文章编号：1001-8409（2015）10-0120-05

Abstract： This paper proposes a reverse logistics network design model for industrial enterprises who recycling the scraped iron and steel. It considers uncertainty of the market demand， collected products quantity and recycled products quality. The objective of reverse logistics network design is to minimize the total costs and minimize the environmental impact. In this paper， a multiobjective stochastic programming model has been established for decisionmaking of recycling plants locations， numbers of plants and collection centers， and material flow distribution between network nodes. Constraint method has been applied to handle multiple objectives into a single objective model. Stochastic programming model is solved combined with scenario analysis. In this paper， numerical examples have been calculated on MATLAB 2014a with CPLEX tool， and the computational result shows that the model is effective. At last， the sensitivity of ε parameters is analyzed.

Key words：reverse logistics； network design； stochastic programming； multiobjective programming

钢铁工业是工业发展的重要组成部分，是国民经济发展中的重要产业，也是国家经济增长的重要支撑之一。我国是世界第一产钢大国，2014年粗钢产量8.23亿吨，占全球粗钢产量的50.26%。我国的废钢资源产生量位居世界之首，达1.6亿吨。废钢铁作为炼钢资源的重要补充，相对于铁矿石炼钢可节能60%，节水40%，分别减少废气、废水和废渣排放86%、76%、97%。每利用1吨废钢可节约1.7吨的铁矿石、0.68吨的焦炭和0.28吨的石灰石。由于我国社会回收废钢网络分散、混乱，回收节点规模小，专业废钢加工配送企业少，导致回收钢质量差，可用率不确定性高，严重影响废钢回收量以及再利用效率，这相比发达国家存在很大的差距。

在上述背景下，钢铁企业的逆向物流逐渐得到重视。逆向物流是将原材料、半成品、产成品和包装从制造商、经销商或消费者流向回收地点或适当处理地点的规划、实施和控制过程，其目的是重新获取价值或对其进行适当处理[1]。逆向物流网络的建设是实现废钢可再回收利用价值的重要保障，对于环境保护、治理及节能减排都具有十分重要的意义。

逆向物流系统的高度复杂性、多样性、供需失衡性使得系统的运作更依赖于物流网络。钢铁企业的逆向物流要向现代化物流方向发展，提高钢铁的回收利用效率。改革废钢的供需体制必须规划建设大型专业化的废钢加工配送网络，从而为钢铁企业实现高效的废钢循环利用网络创造基础条件。

自1990年代Fleischmann提出逆向物流网络研究[2]以来，很多学者开始关注该方面研究。网络设计是当今逆向物流最重要的研究议题之一[3]。学者针对各类产品逆向物流网络提出了定量的设计模型，但研究成果中，国外成果居多，国内研究相对较少。针对电子产品再制造[4， 5]的研究居多，考虑材料循环利用的逆向物流研究较少，且在研究中大部分学者以成本为单一目标，忽略了对环境等方面影响。

CruzRivera和Ertel对墨西哥废弃车辆的回收闭环供应链建立了逆向物流的无容量限制设施选址模型并通过SITATION软件求解[6]。Keyvanshokooh等设计了通用的正向逆向集成物流网络综合决策模型，提出一个多层次、多阶段、多产品和有容量的混合整数线性规划模型[7]。我国学者何波与杨超对固体废弃物回收网络多目标规划的研究中有一些成果[8， 9]。但其对于废弃物回收网络的研究与循环回收利用物流有比较大的区别，避开了需求市场及回收市场中不确定的问题。我国学者李昌兵系统地研究了逆向物流网络选址—路径—库存问题一体优化的混合整数规划模型[10]，但其研究中也未考虑到逆向物流系统中的高度不确定性，而将其作为了进一步可研究的问题。

逆向物流相比正向物流具有更多的不确定性且更复杂。Suyabatmaz等假设回收产品数量是随机的，采用仿真模型解决随机不确定性的逆向物流网络设计问题[11]。Soleimanni等考虑到现实世界的风险参数，建议采用随机优化技术，指出对于选址—分配等规划问题，得出两阶段的随机优化技术是目前最适合最流行的方法的结论[12]。Hatefi和Jolai研究了在风险环境下如何设计健壮可靠的正向—逆向物流网络[13]。在当前研究中，对于不确定性因素的研究，大部分考虑的是客户需求与逆向物流回收量的不确定性，综合考虑回收质量、时间等方面的不确定性研究较少。对于不确定性的研究是逆向物流网络设计未来的研究热点[11]。

本文研究钢铁企业自营逆向物流网络，对钢铁及废钢回收的物流网络集成设计的问题。以企业网络建设中成本最小化和对环境影响最小化为目标，同时在模型中考虑产品需求量、废钢回收量以及回收产品质量的不确定性，建立随机规划模型，最后利用MATLAB调用CPLEX12.6工具箱对模型进行求解和分析。

1问题描述

本文以钢铁企业社会废钢回收利用为背景，建立了多目标多层次的逆向物流网络模型。工厂将钢铁销售给加工厂，经过各类加工最终成为商品进而流通到消费者手中，各类钢铁制品废弃后，经分散的小型回收商回收最终集中到大的回收处理中心，经过初步处理，返回钢厂作为炼钢原料，从而使钢铁资源得到循环利用（如图1所示）。本文以钢铁生产企业自营逆向物流网络为例，对正向物流和逆向物流进行集成优化设计。将加工厂、经销商和消费者等作为需求市场，决策工厂与回收处理中心的建设。决策目标是，在需求市场需求量、回收量和回收质量不确定的情况下，最小化物流网络成本以及对环境的影响，确定设施开放数量、位置和网络节点间物流量的分配。网络示意图如图2所示。

2数学模型

21 参数和决策变量定义

模型中集合定义如下：I指候选工厂地点集合，i∈I；J指需求市场集合，j∈J；K指候选回收处理中心地点集合，k∈K；L指产品种类集合，l∈L。

参数定义如下：A1指产品l的单位生产成本；Bl指工厂与需求市场之间单位产品l单位距离运输成本；Cl指需求市场与回收处理中心之间单位产品l单位距离运输成本；Dl指回收处理中心与工厂之间单位产品l单位距离运输成本；Ei指在地点i开设工厂的固定成本；Fk指在地点k开设回收中心的固定成本；Gl指单位产品l的再循环利用所带来的成本节约；Hjl指需求市场j的回收产品l的单位回收处理成本，由于产品回收质量随机，回收处理成本为随机变量；Pil指工厂i对产品l的容量限制；Qkl指回收中心k对产品l的容量限制；rjl指需求市场j的产品l的回收量，为随机变量；sjl指需求市场j的产品l的需求量，为随机变量；tij指工厂i到需求市场j的距离；tjk指需求市场j到回收中心k的距离；tki指回收中心k到工厂i的距离。

决策变量如下：uijl指工厂i向需求市场j供应的产品l的生产量；vjkl指需求市场j回收至回收处理中心k的产品l的数量；wkil指回收中心k提供给工厂i的产品l的回收量；Xi指是否在地点i开设工厂的决策变量，1表示地点i被选中，否则为0；Yk指是否在地点k开设回收中心的决策变量，1表示地点i被选中，否则为0。

22模型建立

以逆向物流网络中总成本最小化为目标一，包括了工厂与回收中心的固定投资成本、生产成本、回收产品的处理成本、循环利用节约成本和各节点之间的运输成本。同时，考虑在逆向物流网络的建设中，钢铁生产以及废钢回收再利用过程中对环境的影响，包括能源的消耗，废弃物和有害物质的排放，噪声污染以及对居民的影响等。定义参数mil代表候选工厂地点i生产产品l对周围环境影响综合评价指数；nkl代表候选回收处理中心k回收处理产品l过程中的对环境影响综合评价指数。

环境综合评价参数可以通过层次分析、数据包络分析法、模糊综合评价等方法对回收产品材料的循环利用节能减排效能进行综合评价得到综合评价指数。以对环境的影响最小为模型的目标二。

约束（3）确保所有工厂生产产品满足所有需求市场需求；约束（4）表示工厂的容量限制；约束（5）表示回收处理中心的容量限制；约束（6）至约束（8）表示节点流量逻辑限制；约束（9）和约束（10）为变量的取值范围。

23多目标处理

求解多目标优化问题大多数是将向量优化问题转化为标量优化问题，权重法和约束法是两类基本方法。权重法中赋予不同的目标相应的权重，通过目标函数的加权转化为单目标问题，权重法简单易操作，但是一个严重的缺点是权重法只适用于凸集模型；约束法是从全体目标中选择一个作为一个主目标，把其余的目标函数都作为约束条件。约束法理论上对非凸性和凸性问题都适用。Amin等的研究表明，约束法在求解混合整数规划模型时更有效[14]。本文采用约束法思想，以成本最小化目标作为主目标，将目标二转化为模型约束条件：

∑l∑i∑jmiluijl+∑l∑i∑knklwkil≤ε（11）

24情景分析

上述模型中，生产量和回收量以及回收处理产品都是不确定的，假设生产量、回收量和回收处理成本是相互独立的随机变量。本文结合离散的情景分析方法来处理随机变量。设情景集合为ξ1，ξ2，…，ξz，…，ξZ，pξz为情景ξz发生的概率，将模型转化为基于情景的随机规划模型如下：

上述模型属于NP-hard问题，本文在已有研究基础上将情景分析与线性规划相结合来求解上述随机规划模型，在MATLAB 2014a平台中，调用CPLEX对模型算例进行求解。

3算例

31算例描述

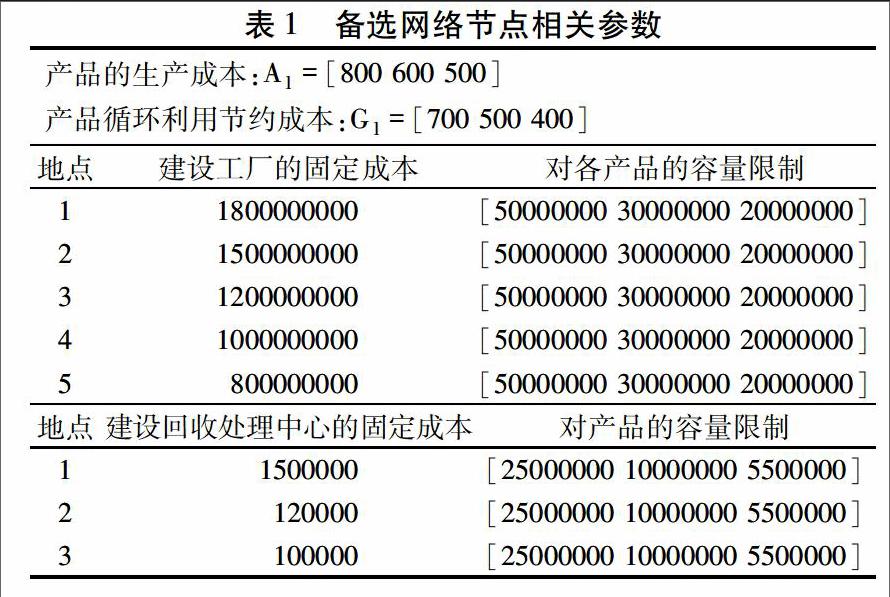
考虑某一大型钢厂建设废钢循环回收利用逆向物流网络，对工厂和回收中心设施网络进行集成设计。已知有5个工厂备选地点、8个需求市场、3个回收中心备选地点，考虑3类不同产品。备选网络节点相关参数见表1。以情景1为基准，考虑不同情况下需求量、回收量和回收产品质量组合下的8种可能发生的情景，参数如表2所示。

32结果分析

（1）首先以情景1为确定性情形，设ε=2000000，对模型进行求解，得最优网络成本为477060万元，此时选中回收中心2，工厂3、4、5，各产品分配如图3a、b、c所示分别是3种产品的网络结构图，其中实线表示正向物流，虚线表示逆向物流。

（2）结合情景分析，基于8个情景求解了随机规划模型，部分情景的参数见表2，每个情景都代表了不同的产品需求量、回收量以及回收产品处理成本的组合。图5显示了基于情景分析的随机规划模型下网络的总成本与每个情景下的确定性模型的网络总成本的对比结果，显示随机规划模型下的总成本处于所有情景的平均水平。

4结论

本文以钢铁企业废钢的循环回收利用为背景，考虑了正向物流与逆向物流网络集成设计的问题。以网络成本的最小化和对环境影响的最小化为目标，建立了多目标规划模型。考虑若干随机的需求市场情景，每种情景下需求市场的需求量、回收产品量、回收产品质量都是不确定的。结合情景分析的方法建立了随机规划模型。该决策模型可支持企业逆向物流网络规划决策。最后，本文在MATLAB R2014a平台调用CPLEX进行求解。应用约束法对目标问题进行处理，在算例分析中对约束参数进行了敏感性分析。针对约束法所存在的局限性，探索进化算法对多目标问题进行处理是进一步的研究方向。另外，针对逆向物流网络的复杂性，可进一步考虑产品返回时间的随机性，使模型更加符合实际。

参考文献：

[1]周垂日，梁樑，许传永，等.逆向物流研究的新进展：文献综述[J].科研管理，2007（03）：123-132.

[2]Fleischmann M， BloemhofRuwaard J M， Dekker R， et al. Quantitative Models for Reverse Logistics： A Review[J]. European Journal of Operational Research， 1997，103（1）：1-17.

[3]Govindan K， Soleimani H， Kannan D. Reverse Logistics and Closedloop Supply Chain： A Comprehensive Review to Explore the Future[J]. European Journal of Operational Research， 2015，240（3）：603-626.

[4]杜茂康，陶波，朱圆.基于三方博弈的废旧家电回收逆向物流激励推进机制研究[J].软科学，2014（12）：55-59.

[5]王文宾，达庆利，聂锐.闭环供应链视角下废旧电器电子产品回收再利用的激励机制与对策[J].软科学，2012（8）：44-48.

[6]CruzRivera R， Ertel J. Reverse Logistics Network Design for the Collection of Endoflife Vehicles in Mexico[J]. European Journal of Operational Research， 2009，196（3）：930-939.

[7]Keyvanshokooh E， Fattahi M， SeyedHosseini S M， et al. A Dynamic Pricing Approach for Returned Products in Integrated Forward/Reverse Logistics Network Design[J]. Applied Mathematical Modelling， 2013，37（24）：10182-10202.

[8]何波，杨超，杨珺.废弃物逆向物流网络设计的多目标优化模型[J].工业工程与管理，2007（5）：43-46.

[9]何波，杨超，张华.废弃物回收的多层逆向物流网络优化设计问题研究[J].中国管理科学，2007，15（3）：61-67.

[10]李昌兵，张斐敏.集成选址—路径—库存问题的逆向物流网络优化[J].计算机集成制造系统，2014（7）：1793-1798.

[11]Suyabatmaz A C， Altekin F T， Sahin G. Hybrid Simulationanalytical Modeling Approaches for the Reverse Logistics Network Design of a Thirdparty Logistics Provider[J]. Computers & Industrial Engineering， 2014，70：74-89.

[12]Soleimani H， Govindan K. Reverse Logistics Network Design and Planning Utilizing Conditional Value at Risk[J]. European Journal of Operational Research， 2014，237（2）：487-497.

[13]Hatefi S M， Jolai F. Robust and Reliable Forwardreverse Logistics Network Design under Demand Uncertainty and Facility Disruptions[J]. Applied Mathematical Modelling， 2014，38（9-10）：2630-2647.

[14]Amin S H， Zhang G. A Multiobjective Facility Location Model for Closedloop Supply Chain Network under Uncertain Demand and Return[J]. Applied Mathematical Modelling， 2013，37（6）：4165-4176.

（责任编辑：杨锐）