对偶四元数遥感影像区域网平差精度分析

肖晖，费利佳

1.安徽大学资源与环境工程学院，合肥230601 2.南京晓庄学院生物化工与环境工程学院，南京211171 3.南京航空航天大学航天学院，南京210016

对偶四元数遥感影像区域网平差精度分析

肖晖1，2，费利佳3

1.安徽大学资源与环境工程学院，合肥230601 2.南京晓庄学院生物化工与环境工程学院，南京211171 3.南京航空航天大学航天学院，南京210016

根据几何代数理论，提出对偶四元数区域网平差方法，采用对偶四元数描述区域网像坐标系间的旋转和平移，对严格共线条件方程进行线性化，按照带有约束条件的间接平差进行迭代解算.对偶四元数区域网平差模型法方程式的结构完全类似于传统方法，所需计算机内存单位由于边宽的增加而略有增加.实验结果表明，对偶四元数区域网平差在影像的4个定点与中心布置控制点，能达到较高的测量精度.

摄影测量；区域网平差；几何代数；间接平差；法方程式

区域网平差是从原始的影像坐标观测值出发建立平差数学模型，能最佳地顾及并改正影像系统误差的影响.随着摄影测量技术的发展和计算机水平的提高，这种最严密的平差方法已得到泛应用［1-2］.如今，无飞机、飞艇等低空平台逐渐应用于航空摄影测量作业［3］.由于这类平台的不稳定性，相对于传统航摄飞机，由无人机和飞挺等低空平台摄得的像片一般不能满足旋转角小于3◦的航摄要求，这给传统的空三测量作业带来了一定的困难.

现有的平差解算方法有欧拉角法、矩阵分解法［4］及单位四元数法［5］，其中前两种方法在计算过程中包含繁琐的三角函数计算，计算量大；单位四元数法虽然可用角元素的四元数来表示，减少了平差运算量，但仅仅解决了坐标系之间的旋转变换.由于一次变换无法同时解决平移问题，于是将对偶四元数引入平差解算.

对偶数是由Clifford为研究旋量代数引入对偶单位加以定义的，随后由Study进行完善.与其他可用来描述螺旋运动的方法相比，对偶数被证实是最简洁而有效的［6］.Charles定理表明，任何一般性刚体运动都可以等效成螺旋运动，而对偶四元数把转动和平移统一考虑，是描述螺旋运动最简洁的几何代数工具［7］.近年来，对偶四元数已广泛应用于机器人运动学［8］、航天器交会对接［9］、运动目标姿态确定［10］、多刚体系统［11］和计算机视觉［12］等领域.文献［13］通过实验验证了对偶四元数成像几何模型在对地定位中的正确性和普适性.

1　对偶四元数

1.1对偶数与对偶四元数

式中，a为对偶数的实部，b为对偶部，其中ε2=0且ε/=0.

对偶四元数是在四元数和对偶代数理论的基础上提出的，是可以将平移和旋转统一描述的有效手段.对偶四元数可描述为

对偶数是一种几何代数，由实部和对偶部组成，可表示为

式中，ε2=0且ε/=0.其中，q=q0+iq1+jq2+kq3，q′=q′0+iq′1+jq′2+kq′3均为四元数，分别称为对偶四元数的实部和对偶部.

1.2基于对偶四元数的坐标转换

如图1所示，对偶四元数可以实现坐标变换［14］

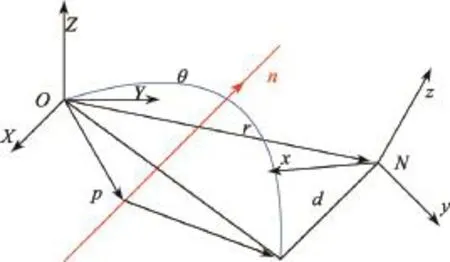
图1　对偶四元数描述的坐标转换Figure 1 Coordinate transformation based on dual quaternion

坐标系O绕着空间矢量n旋转θ角度，同时沿着n平移d形成新坐标系N.该过程实质上是刚体的一般空间运动，其中p为坐标系原点O到旋转轴上某一点间的向量.由图1可以看出，只要给定对偶矢量n和对偶角对偶四元数就可以非常简洁地表示空间坐标由O系到N系的变换关系.

假设目标坐标系为N-xyz，待转换坐标系为O-XY Z.两坐标系相对位置和姿态即为坐标系O-XY Z相对于坐标系N-xyz的螺旋运动，可由四元数描述为

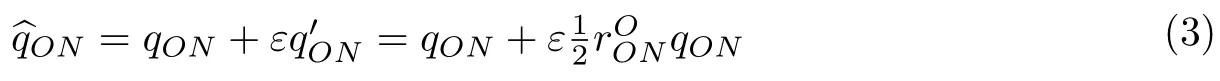
2　对偶四元数区域网平差

区域网平差能用摄影测量解析法确定区域内所有影像拍摄时刻探测器的位置和姿态，其原理如下：直接由每幅影像的光束出发，以像点坐标为观测值，通过每个光线束在三维空间的平移和旋转，使同名光线在物方最佳地交会在一起，并使之纳入规定的坐标系，从而求出每幅影像拍摄时刻的位置和姿态，因此从理论上来说是最严密的.利用对偶四元数严密成像几何模型进行区域网平差，其思想是将时间序列影像的姿态和相对位置用对偶四元数统一处理，从而补偿成像几何模型的系统误差.

2.1区域网平差模型

基于对偶四元数的平差示意图如图2所示，点A为影像1～4上4条光线的交点.以OS1光线束为例，当探测器运动到位置S1时，传感器拍摄地面点形成摄影光束，此时S1-x1y1z1、S1-ω1u1ν1、O-XY Z转动的角方位元素可写成2个对偶角的形式.将线方位元素矢量类比成S1-x1y1z1和O-XY Z的位移矢，由对偶四元数并利用公式可以将S1-x1y1z1做螺旋运动变换到O-XY Z中.

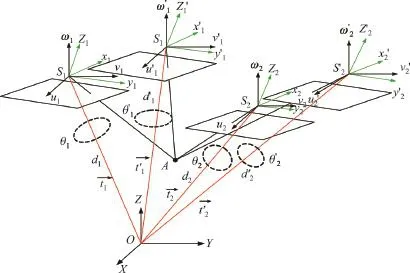
图2　对偶四元数区域网平差模型Figure 2 Bundle adjustment based on dual quaternion

基于对偶四元数的区域网平差的中心投影构像方程，旋转变换矩阵和平移变换矩阵见参考文献［13］.

2.2平差模型

法方程式的结构为

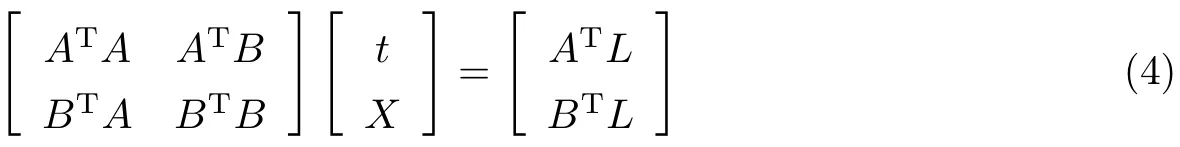
如果有n（i=1，2，···n）张像片，参与平差的模型点数目为t，控制点数目为n1，检查点数目为n2（t=n1+n2），计入模型点重叠度的像点数目为m，对于每个控制点结合其自身在平差影像区域内的分布，可列出相应的误差方程式.

对于每张像片都存在限制条件方程

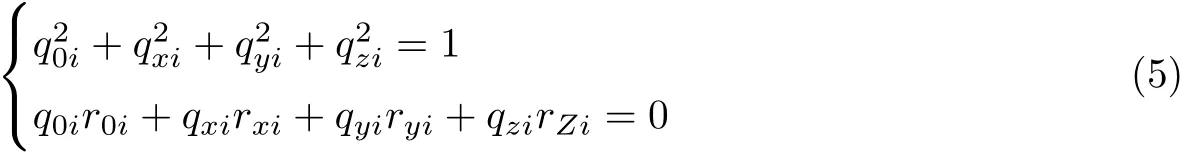
因此，整体平差的误差方程式为

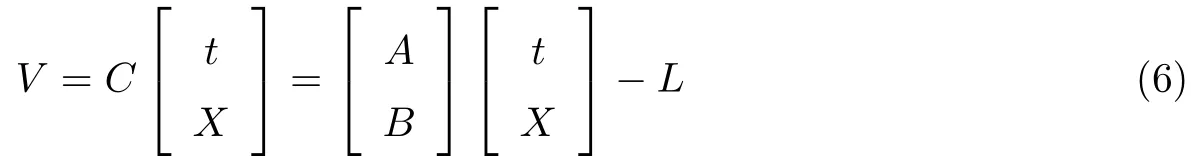
式中，V和L为2t×1的矩阵，C为2m×（8n+3n2）的矩阵，则

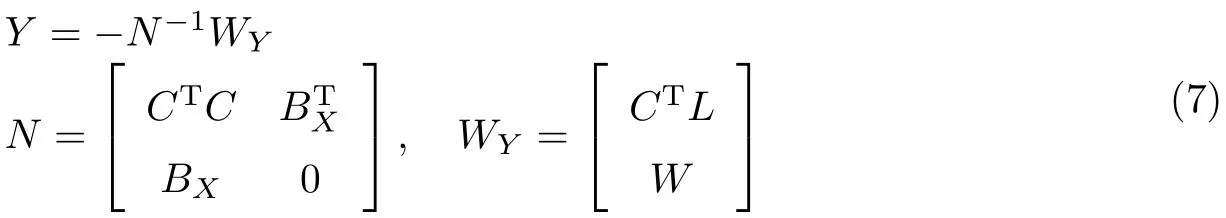
2.3法方程式结构及其分析

现有一个理想的1×3摄影测量区域如图3所示，矩形的边表示影像A、B、C，Δ为平高控制点，O为待加密的模型点.控制点点0和6、待加密的模型点10、11、12和16是由影像A和B上的两条光线得到的；其他控制点和待加密的模型点是由影像A、B、C上的3条光线得到的.

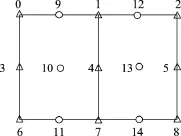
图3　控制点与检查点分布图Figure 3 Distribution of control points and check poiuts

误差方程式系数矩阵结构如图4所示，待加密的模型点9是由影像A、B、C上的3条光线得到的，因此非0元素占6行.该点在每张影像上可以列出6个误差方程式，每个误差方程式有8个未知数，为该影像对偶四元数，而该模型点的各个坐标改正数分别用6行连成一个竖向的矩形来表示.待加密的模型点10是由影像A和B的两条光线得到的，因此非0元素占有4行.该点在每张影像上可以列出4个误差方程式，而该模型点的各个坐标改正数分别用4行连成一个竖向的矩形来表示.

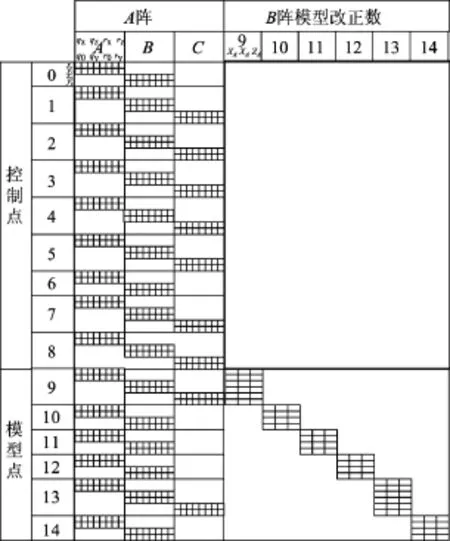
图4　误差方程式系数矩阵Figure 4 Matrix of the error equation coefficient

相应的法方程式未知数的系数矩阵结构如图5所示，是对称带状稀疏矩阵.每张影像ATA的阶为8×8，每个模型点BTB的阶为3×3，分别对应主对角线上每个大方块（阶数为8×8）和每个小方块（阶数为3×3）；全区待定点有6个，则相应的BTB的阶数为18×18；非主对角线上的矩形反映了每张像片上有关待求的模型点的内容，对于待加密的模型点9，ATB的阶为（8×3）×3；由于约束条件式（7）引入平差模型中，原法方程系数阵的内容仅增加了与t有关的镶边部分D，且其阶为8×2.因此，对偶四元数空中三角测量平差法方程系数阵在结构上完全类似于传统的区域网平差，只是所需计算机内存单位由于边宽的增加而略有增加.

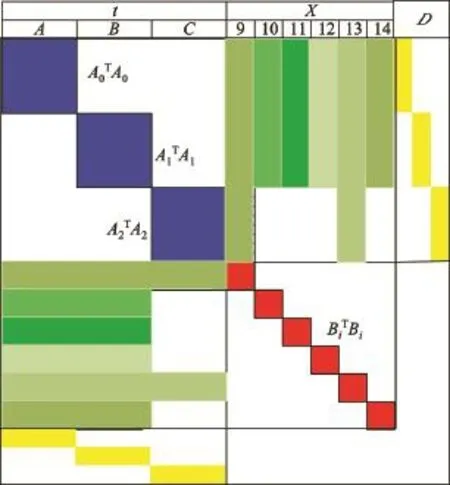
图5　法方程式未知数系数矩阵Figure 5 Matrix of the normal equation coefficient

3　实验结果及分析

下面利用RC30航摄仪实际影像数据进行平差，说明对偶四元数区域网平差模型在提高探测器定位精度方面的可靠性.对航空影像，共计2条航带6张影像，摄影比例尺为1∶15 000，相机焦距为0.152 72 m，旁向重叠为30%，航向重叠为66%，飞行高度约为2 290 m.区域内最大高差为303 m，属于山区地形.

对上述影像，采用表1中的7种不同控制点布设方案，利用对偶四元数方案进行区域网平差解算.在平差计算过程中，认为所有像点的坐标都是等精度且不相关的观测值，因此权矩阵P为单位阵.影像数据包含已知的位置和姿态信息，且解算时所必需的位姿初始值作为已知值给定.图中，十字丝中心（直线的某个端点）代表检查空间位置，直线代表残差偏移方向和大小.本文衡量精度的标准如下：一是由计算加密点X、Y、Z方向的误差得到平面与高程残差分布图，二是由X、Y方向的精度求出平差的平面精度.实验结果见表1，可以看出由本文提出的基于对偶四元数的区域网平差方法解算得到的实际平高精度均与理论精度相近，证明了该算法的可靠性.迭代次数为3～4次，迭代速度快，因此计算时间少.

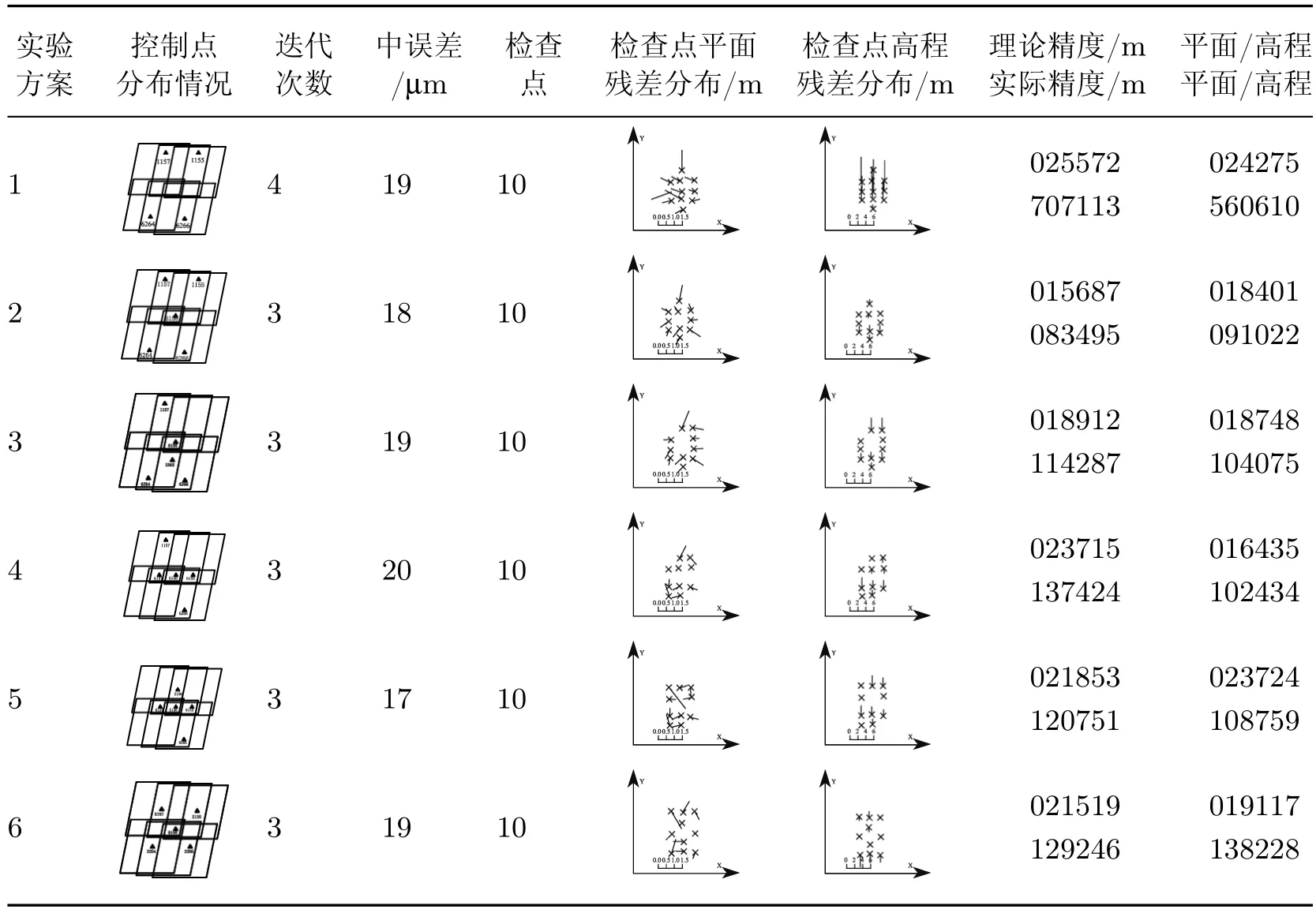
表1　不同控制点布设方案的区域网平差精度Table 1 Accuracy of bundle adjustment for diferent programs of control points distribution

表1中，Δ为平高控制点；实际精度由n个加密点坐标与真实坐标差值求出，即= X，Y，Z，µ平面=；理论精度由误差传播定律求得，即=X，Y，Z，m平面=

6组实验的检查点残差存在明显的规律性，采用多元回归方程分析残差分布

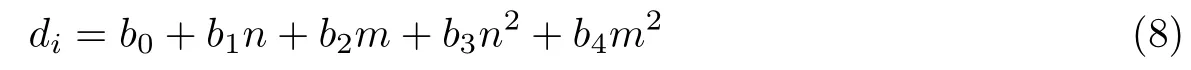
式中，bj（j=0，1，2，3，4）为待回归分析的5个回归系数；1，n，m，n2，m2是与回归系数对应的自变量（因子），n为边缘控制点数目，m为内部控制点数目；di为随机变量，i=x，y，z，xy，分别表示x和y方向精度、高程与平面精度，实验结果如表2所示.

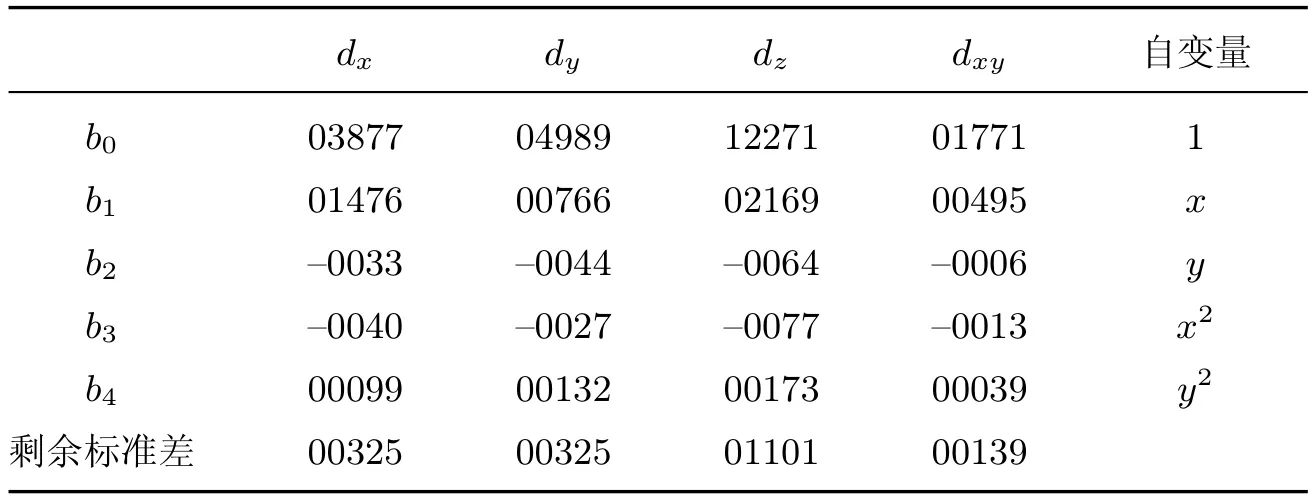
表2　回归分析结果Table 2 Results of regression analysis

比较自变量x与y，x2与y2的系数可以发现：b1＞b2，b3＞b4.边缘控制点的数目对平高精度的影响大于内部控制点，即光束法区域网平差精度最弱的点位于区域的四周；对于区域网平差区域，内部的精度较高而且均匀，精度薄弱环节在区域的四周.因此，在保证区域中心存在控制点的情况下，平面控制点应当尽量布设在区域的四周，这样才能起到控制精度的作用.如果控制点的布设合理，就能在保持平高精度基本不变的前提下减少控制点的数量，大大减少为获取控制点而增加的工作量.

4　结语

对偶四元数方法用于机载遥感影像区域网平差，其实际精度与理论精度相当，可作为数字摄影测量学的一种全新的具有独特优势的探索.与传统欧拉角方法相比，计算时避免了繁琐的三角函数运算，迭代速度快，且适用于不稳定航摄平台影像和近景影像区域网平差.在传统的空三测量中，由于地形的复杂性和航片质量等问题，不能保证每张航摄像片都能获取大量的、均匀分布的加密点，因此对偶四元数法在空中三角测量中具有较好的应用前景.然而，对偶四元数方法的稳定性有待进一步研究，如在低空摄影测量中，应充分发挥该方法在大姿态角影像定向元素求解上的独特优势，以获得更稳定的求解方案.

［1］张剑清，潘励，王树根.摄影测量学［M］.武汉：武汉大学出版社，2009：87-90.

［2］王任享，王建荣，胡莘.EFP全三线交会光束法平差［J］.武汉大学学报：信息科学版，2014（7）：757-761. Wang R X，Wang J R，Hu X.The EFP bundle adjustment of all three line intersection［J］. Geomatics and Information Science of Wuhan University，2014（7）：757-761.（in Chinese）

［3］朱锋，肖晖，魏亚男.无人机遥感影像镶嵌技术综述［J］.计算机工程与应用，2014，50（15）：38-41. Zhu F，Xiao H，Wei Y N.Summary of UAV remote sensing image mosaicking technology［J］. Computer Engineering and Applications，2014，50（15）：38-41.（in Chinese）

［4］杜治全，郑顺义.光束法平差的一种快速算法［J］.地理空间信息，2007，5（1）：78-80. Du Z Q，Zheng S Y.A fast algorithm for bundle adjustment［J］.Geospatial Information，2007，5（1）：78-80.（in Chinese）

［5］季顺平，吴珍丽.单位四元数在航空摄影测量解算中的应用与实践［J］.测绘科学，2010，35（1）：311-316. Ji S P，Wu Z L.The application and practice of unit quaternion method in aerial triangulation［J］.Science of Surveying and Mapping，2010，35（1）：311-316.（in Chinese）

［6］Brodsky V，Shohan M.Dual numbers representation of rigid body dynamics［J］.Mechanism and Machine Theory，1999，34（5）：693-718.

［7］MarTinea J M R，DuFFy J.The principle of transference：history，statement and proof［J］. Mechanisms and Machine Theory，1993，26（1）：165-177.

［8］Wang X K，Yu C B，Lin Z Y.A dual quaternion solution to attitude and position control for rigid-body coordination［J］.IEEE Transactions on Robotics，2012，28（5）：1162-1170.

［9］钱萍，王惠南.基于对偶四元数的航天器交会对接位姿双目视觉测量算法［J］.宇航学报，2013，34（1）：32-38. Qian P，Wang H N.Algorithm of vision measure for relative position and pose of RVD spacecrafts based on dual-quaternion［J］.Journal of Astronautics，2013，34（1）：32-38.（in Chinese）

［10］冯国虎，章大勇，吴文启.单目视觉下基于对偶四元数的运动目标位姿确定［J］.武汉大学学报：信息科学版，2010，35（10）：1147-1150. Feng G H，Zhang D Y，Wu W Q.Pose estimation of moving object based on dual quaternion from monocular camera［J］.Geomatics and Information Science of Wuhan University，2010，35（10）：1147-1150.（in Chinese）

［11］Schlanbusch R，KrisTiansen R，Nicklassom P J.On choosing quaternion equilibrium point in attitude stabilization［C］//International conference on aerospace，Montana，Alberta：University of Montana，2010：410-417.

［12］Wang Y B，Wang Y J，Wu K，Yang H C，Zhang H.A dual quaternion-based，closed-form pairwise registration algorithm for point clouds［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2014，94：63-69.

［13］姬亭，盛庆红，刘微微，王惠南.对偶四元数单片空间后方交会算法［J］.中国图象图形学报，2012，17（4）：494-503. Ji T，Sheng Q H，Liu W W，Wang H N.Dual quaternion of space resection with single image［J］.Journal of Image and Graphics，2012，17（4）：494-503.（in Chinese）

［14］ATa E，Yayli Y.Dual quaternions and dual projective spaces［J］.Chaos，Solitons and Fractals，2009，40（3）：1255-1263.

（编辑：秦巍）

Accuracy Analysis of Region Adjustment of Remote Sensing Images Based on Dual Quaternion

XIAO Hui1，2，FEI Li-jia3
1.College of Resource and Environmental Engineering，Anhui University，Hefei 230601，China 2.School of Biochemical and Environmental Engineering，Nanjing Xiaozhuang University，Nanjing 211171，China 3.College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China

According to the geometric algebra theory，a bundle adjustment method based on dual quaternion is presented.The method uses dual quaternion to describe rotation and translation of regional photo coordinates，and can linearize a strict collinearity equation.Constraint parameter adjustment is iteratively computed.The structure of normal equation in region adjustment based on dual quaternion is similar to that of traditional methods，with the required memory slightly increased with the increasing margins.The results show that，by arranging control points in four angle points and central point，the dual quaternion-based region adjustment can achieve relatively high measuring accuracy.

photogrammetry，region adjustment，geometric algebra，parameter adjustment，normal equation

P23

0255-8297（2015）01-0079-08

10.3969/j.issn.0255-8297.2015.01.009

2014-05-26；

2014-10-21

国家自然科学基金（No.41101441）资助

肖晖，博士，讲师，研究方向：遥感影像几何定位，E-mail：xiaohui257@qq.com