一种改进的强跟踪滤波算法
钱华明,葛磊,2,黄蔚
1.哈尔滨工程大学自动化学院,哈尔滨150001 2.中国航天科工集团二院706所,北京100854
一种改进的强跟踪滤波算法
钱华明1,葛磊1,2,黄蔚1
1.哈尔滨工程大学自动化学院,哈尔滨150001 2.中国航天科工集团二院706所,北京100854
强跟踪滤波算法由于对判断滤波发散的阈值设置较小,以较大概率产生渐消因子而导致对滤波增益过调节,最终对状态估计不够平滑.在分析强跟踪滤波算法运行机理的基础上,提出了一种改进的强跟踪滤波算法.通过适当提高判断滤波发散的阈值,有效降低了误判滤波发散的概率,并能针对不同维数量测方程确定不同的弱化因子,避免了凭经验加入弱化因子解决这一问题的缺陷.数值仿真结果表明:改进的强跟踪滤波算法对系统状态突变不但具有较强的鲁棒性,而且能有效保持滤波精度和对状态估计的平滑性,从而验证了该算法的可行性和有效性.
强跟踪滤波;鲁棒性;渐消因子;弱化因子
在现代估计理论中,卡尔曼滤波(Kalman filter,KF)具有重要的地位,但对于模型误差鲁棒性不强,严重时甚至发散[1].为了提高KF的估计精度,阻止其发散,文献[2-3]提出了渐消滤波算法.该算法在滤波方程中加入渐消因子,降低了旧量测值对滤波估计的修正作用,增加了新量测值在滤波估计中的权重,有效抑制了滤波发散.文献[4]基于渐消滤波算法思想,提出了可以自适应地求取最佳渐消因子的强跟踪滤波(strong tracking filter,STF)算法,根据强迫残差序列正交的方法来确定最佳渐消因子,使得滤波在具有模型误差和状态突变时仍能很好地跟踪状态的变化.该算法具有较强的鲁棒性和较高的估计精度,因此得到了广泛应用[5-8];但对状态估计不够平滑,即使引入弱化因子加以调节(弱化因子需要凭经验选取),也难以在实际中应用[9-10].
本文深入研究了STF算法的理论基础,并将其应用于一维线性系统.STF算法对判断滤波发散的阈值设置较小,使误判滤波发散的概率增大,即使在系统正常的情况下,产生渐消因子的概率仍然较大,导致对滤波增益的过度调节,影响了状态估计的平滑性.为此,本文提出了改进的强跟踪滤波(improved STF,ISTF)算法,通过适当增大判断滤波发散的阈值,降低了误判滤波发散的概率,有效弥补了对状态估计不平滑的缺点,且不必凭经验选取弱化因子,使其在实际应用中更便利.
1 STF算法
考虑如下的线性模型:

式中,wk、vk为零均值的高斯白噪声,其协方差分别为
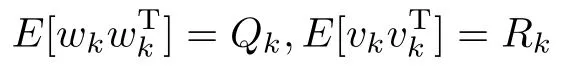
则STF算法的递推公式如下:
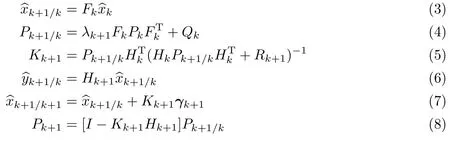
其中
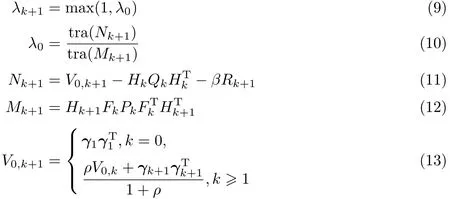

式中,tra(·)表示对矩阵求迹;ρ为遗忘因子,一般取ρ=0.95;β≥1为弱化因子,它可以使状态估计值更加平滑,通常β≥1凭经验选取.同样需要说明的是,V0,k+1并没有理论上的求解方法,故只能依靠输出残差序列的加权和近似获得[4-6].
若系统模型为非线性,即

则非线性系统下的强跟踪扩展卡尔曼滤波(strong tracking extended Kalman filter,STEKF)算法应将一步状态预测方程和一步量测预测方程改成如下形式:

式中,Fk和Hk+1可分别以系统方程和量测方程的雅可比矩阵来代替,即
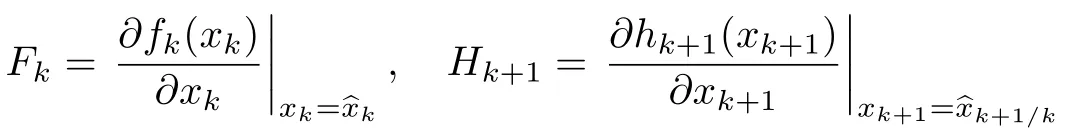
其他方程不变.
2 STF算法分析
2.1STF算法原理分析
当系统模型正常时,在最优滤波条件下,系统输出的残差应该是互不相关的高斯白噪声序列[11-14],即
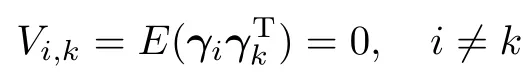
且
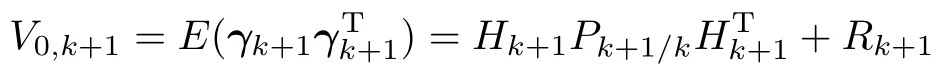
当系统具有模型误差或者状态突变时,V0,k+1变大,从而使得
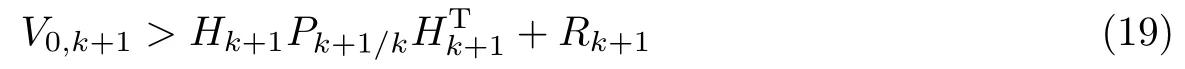
在强跟踪滤波算法中,为了保证滤波的最优性,需要将Pk放大λk+1倍,强迫输出的残差序列相互正交,即令
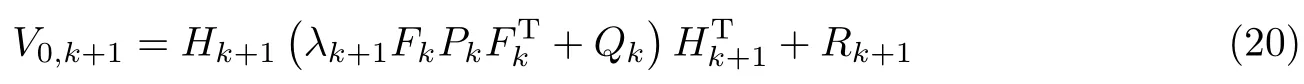
根据式(20)即可求出λk+1,不但抑制了滤波发散,而且得到了最佳的滤波结果.
分析式(19)和(20)可知,可以将强跟踪滤波对λk+1的调整认为是对V0,k+1设置了一个阈值Hk+1Pk+1/kHTk+1+Rk+1.若满足则判定滤波异常,出现发散情况,需要根据式(20)求取λk+1;否则,λk+1=1,即为正常的卡尔曼滤波公式.
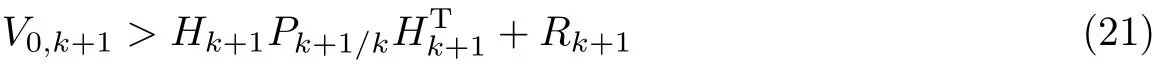
然而在实际应用中发现,强跟踪滤波对状态的估计不够平滑,于是加入弱化因子β来克服这个问题.弱化因子的选取并没有具体的公式,而只能靠经验选取,这给实际应用带来了不便.
2.2STF算法问题分析
本节将STF应用于正常情况下的一维线性系统,以分析产生上述问题的原因.
由于分析的系统为一维,滤波方程中的每一项皆为标量;但为了便于理解,以及向多维系统STF进行扩展,滤波方程仍然以向量形式表示.
显然,当系统模型准确且没有状态突变时,KF为最优滤波,此时若应用STF,则滤波方程应当尽量保持与KF滤波方程一致,较少地产生大于1的渐消因子,才能得到较好的估计结果,且使估计曲线更加平滑.
应用STF时,由于V0,k+1没有解析解,而只能通过残差序列加权求和近似得到,使得近似值与理论值相比,会有一定概率产生较大偏差,而较大的偏差导致滤波结果不够平滑.证明如下:
为了表示与k+1次输出残差方差近似值V0,k+1的区别,以C0,k+1表示其理论值,则有
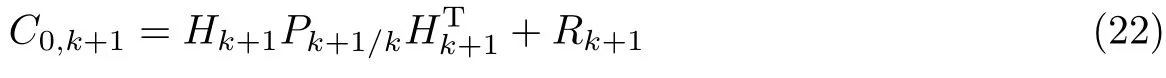
当k≥1,ρ=0.95时,有
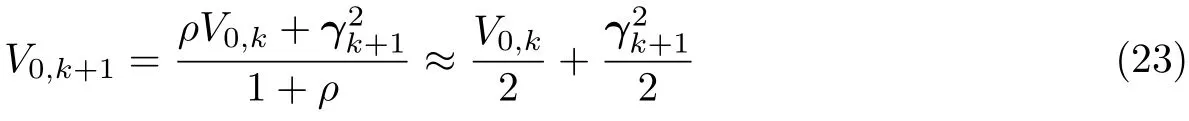
由KF理论可知,γk+1服从均值为0、方差为C0,k+1的高斯分布.在滤波过程中,对于k+1时刻得到的残差γk+1,可以认为是对高斯分布N(γk+1;0,C0,k+1)的一次采样,根据概率论的知识可知
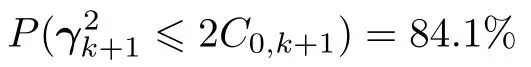
此时判断滤波发散的概率
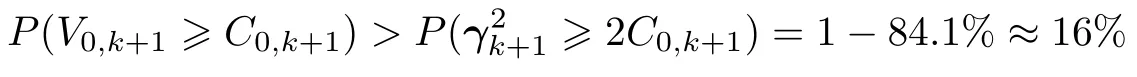
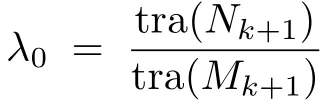
以上两个原因导致STF对状态估计过分依赖量测值,使得滤波增益达不到最优,导致估计效果不够平滑.
若在Nk+1中加入弱化因子β,则将阈值增大为,相当于提高了判断滤波发散的阈值,减少了在正常情况下产生渐消因子λk的概率.然而,阈值C0,k+1还与Pk+1/k有关.对于不同系统,单纯地调整β没有规律可寻,而只能凭经验或试验选取,故缺乏可操作性.
3 ISTF算法
由2.2的分析可知,STF对状态估计不够平滑的主要原因如下:对V0,k+1的近似不够准确,导致对判定滤波异常的阈值设置较小,即使在系统正常情况下,也有较大的概率被视为滤波异常,从而产生渐消因子,破坏了滤波的最优性.要使STF的估计曲线更加平滑,以提高STF的滤波精度,则应适当增大判断滤波发散的阈值,在保证对模型失配和状态突变具有较强鲁棒性的同时,使系统在正常工作情况下产生尽可能少的渐消因子.
由于
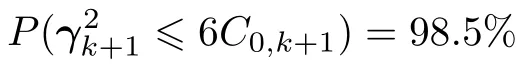
可知
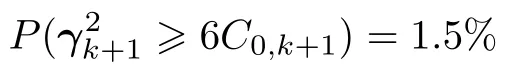
于是可将阈值提高到3C0,k+1,此时如果不考虑V0,k,则有
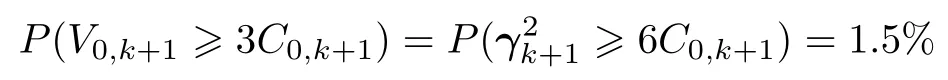
如果考虑V0,k的影响,由于V0,k<C0,k+1,即使假设两者相等,仍有
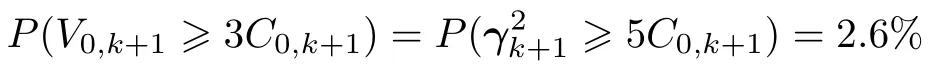
因此,当将V0,k+1的阈值取到3C0,k+1时,STF算法在正常工作情况下误判滤波发散的概率下降到1.5%~2.6%,于是大大降低了产生渐消因子的几率,使得STF更加接近KF.对于因状态突变或模型不准确导致的误差,如果其方差小于3C0,k+1,则可视为合理的高斯白噪声,直接利用KF处理.
当系统具有模型误差或状态突变时,将阈值取为3C0,k+1,则有
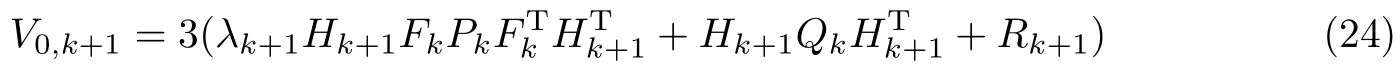
从而有
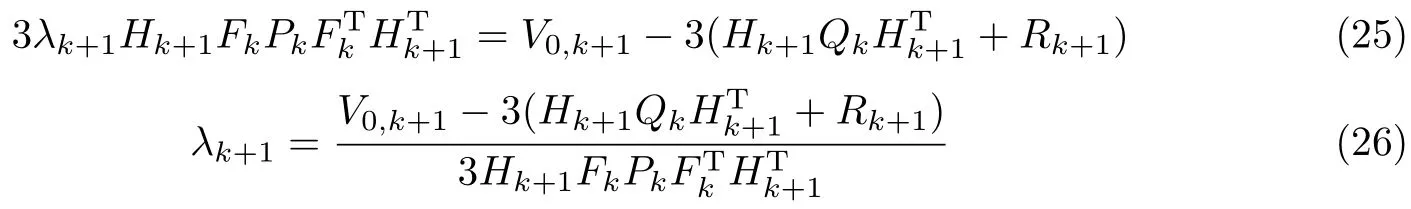
可得到ISTF算法的渐消因子
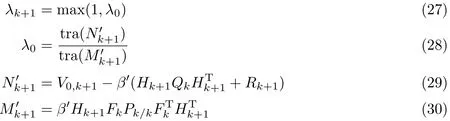
弱化因子β′=3,这样结合式(3)~(8)便构成了ISTF算法.
与原STF算法相比,改进的算法对Nk+1和Mk+1进行调整,并增加了针对Hk+1Qk和Hk+1FkPk的固定弱化因子β′=3,能避免通过经验选取弱化因子的麻烦;同时新算法仍然强迫输出的残差序列正交,也能保证滤波的最优性.
以上关于ISTF算法推导均基于一维系统,但也可以推广到多维系统上.当推广到多维系统时,在理论推导上需稍作改变,弱化因子也要适当调整,此时STF算法判断滤波异常的条件为

仍然假设V0,k=C0,k+1,则式(31)等价为
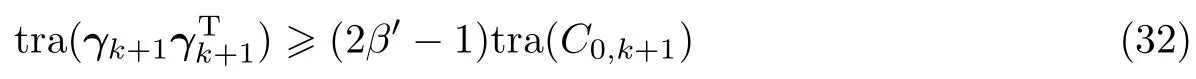

式中,n为观测向量的维数.
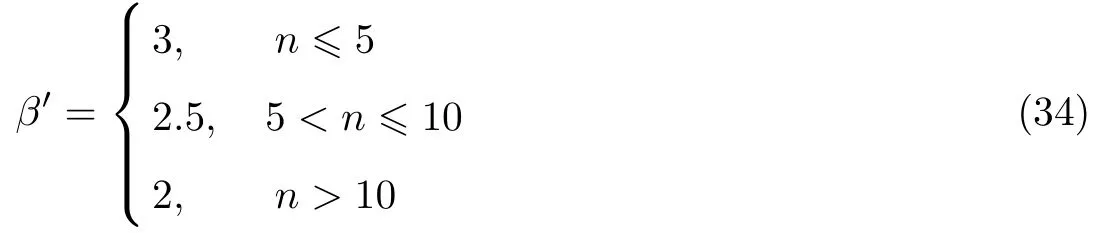
此时β′的取值可以看作是对ISTF鲁棒性和平滑性的一个折中.如果β′取值较小,则算法的鲁棒性较强,对状态突变和模型误差的跟踪性强,但对滤波发散的误判概率较高,估计效果不够平滑;如果β′取值较大,则误判滤波发散的概率变小,降低了产生大于1的渐消因子概率,况且渐消因子较小,导致对模型失配和状态突变不够敏感,鲁棒性减弱,甚至可能使算法退化为普通的KF或EKF.
若非线性系统采用线性化的EKF算法,则带来一定的截断误差,而这些误差会影响所设计的强跟踪滤波算法的性能,因此在求取渐消因子时必须加以考虑.根据文献[15]的理论,可以将非线性系统线性化带来的误差看作虚拟白噪声.为了保证算法的鲁棒性,可以适当将虚拟白噪声的协方差扩大.假设由线性化引起的系统虚拟噪声和量测虚拟噪声的协方差分别为0.5Qk和0.5Rk+1,此时可认为系统噪声和量测噪声协方差为1.5Qk和1.5Rk+1,则渐消因子和弱化因子的关系为
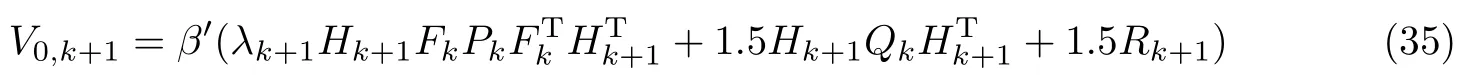
从而对于非线性系统,ISTEKF的渐消因子可以解得
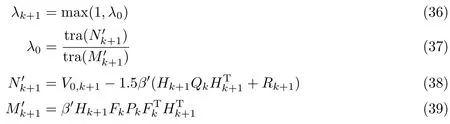
式中,β′按照式(34)取值.
4 数值仿真及分析
本文采用文献[4]给出的非线性系统模型来验证所提出改进算法的有效性,其非线性模型如下:
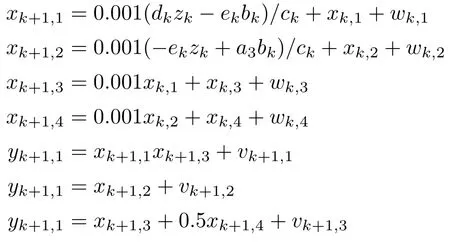
式中
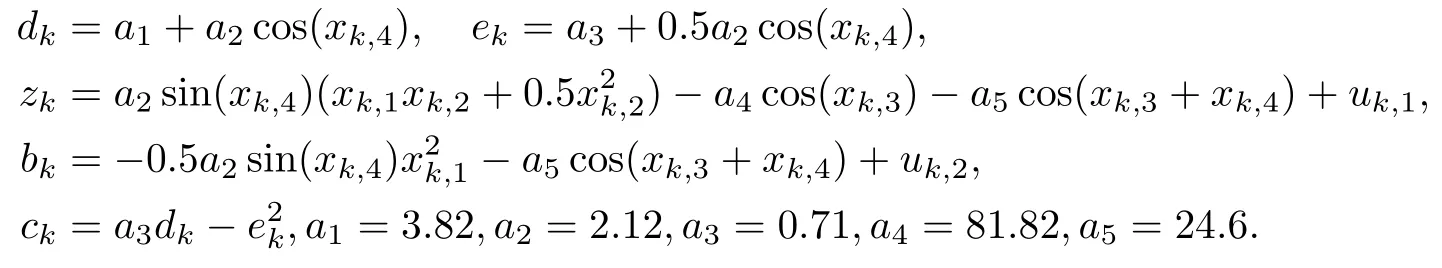
在滤波过程中设
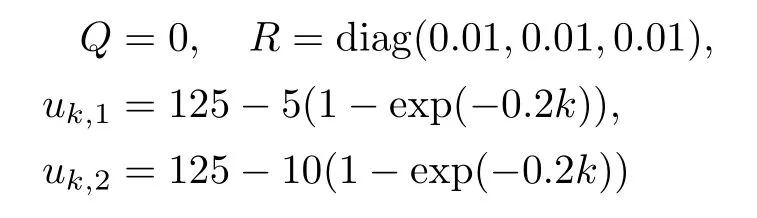
仿真时间为200s,同时假设当k=70和k=140时,由于外部强干扰,xk,1分别有+4和-3的突变,于是分别使用EKF、STEKF(弱化因子为1)和本文提出的ISTEKF对系统进行滤波.对于ISTEKF,由于量测向量的维数为n=3,则根据式(34)可知弱化因子取β′=3较为合适.为了验证本文所取β′的合理性,又分别取β′=2,β′=6两种情况进行比较,此时得到的状态xk,1的估计曲线和渐消因子的响应曲线分别如图1和2所示.
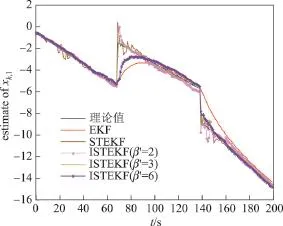
图1 xk,1的估计曲线Figure 1 Estimate of xk,1
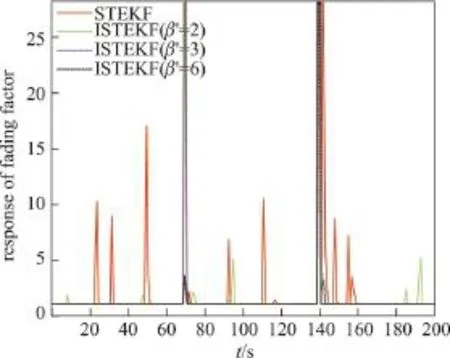
图2 渐消因子响应曲线Figure 2 Response of fading factors
由图1可知,EKF不能跟踪状态的突变,且鲁棒性较差;而STEKF和本文提出的ISTEKF(β′=2,β′=3)都能对状态的突变迅速反应,具有较强的跟踪能力.然而,STEKF对状态的估计不够平滑,不论是否发生状态突变,STEKF都会围绕理论值产生抖动;ISTEKF(β′= 2)的光滑性好于STEKF,且较ISTEKF(β′=3)稍差;ISTEKF(β′=3)的估计结果最平滑,即使有状态突变,仍能快速跟踪真实状态,且围绕理论值抖动时间较短,估计结果更精确;ISTEKF(β′=6)的跟踪能力较弱,不能对状态突变快速反应,其原因在于β′的设置过大,导致算法对模型失配和状态突变不敏感,这也验证了前面的理论分析.
由图2可知,STEKF在较多时刻产生了大于1的渐消因子,在状态突变时产生的渐消因子较大,在状态未突变时产生的渐消因子较小.正是由于STEKF在状态未突变时产生了较多大于1的渐消因子,才会使滤波估计过分依赖量测值,导致对状态估计不够平滑;ISTEKF(β′=2)产生的渐消因子少于STEKF,但也在状态未突变时产生了大于1的渐消因子,影响了估计效果;ISTEKF(β′=3)只在状态发生突变后产生大于1的渐消因子,并且渐消因子迅速减小,直到下降为1,这样避免了对滤波增益的过调节,保证了较好的估计效果;ISTEKF(β′=6)也只在状态突变后产生大于1的渐消因子,但β′设置过大会导致渐消因子较小,产生的滤波增益也较小,降低了对量测值的依赖程度,减弱了对状态突变的跟踪能力.
5 结语
STF算法对模型失配和状态突变的系统具有良好的鲁棒性,但对状态估计的结果不够平滑,需要加入弱化因子来调整.然而,弱化因子没有确定的求取方法,对不同系统只能通过试验或经验选取,因此在实际应用中不够便利.为此,本文提出了ISTF算法,通过适当提高判断滤波发散的阈值,降低了误判滤波发散的概率,较为合理地产生大于1的渐消因子,并针对不同维数的观测方程选取不同弱化因子.理论分析和仿真结果表明,ISTF算法能在保持鲁棒性的同时有效提高滤波精度,使状态估计曲线更加平滑,具有实用价值.
[1]Husoy J H,Abadi M S E.Unifed approach to adaptive flters and their performance[J].IET Signal Processing,2008,2(2):97-109.
[2]Sorenson H W,Sacks J E.Recursive fading memory fltering[J].Information Sciences,1971,3(2):101-119.
[3]YdsTid B E,Co T.Recursive estimation with adaptive divergence control[J].IEEE Proceeding Control Theory and Applications,1985,132(3):124-130.
[4]周东华,席裕庚,张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991,17(6):689-695. Zhou D H,Xi Y G,Zhang Z J.A suboptimal multiple fading extended Kalman flter[J].Acta Automation Sinica,1991,17(6):689-695.(in Chinese)
[5]鲍其莲,孙朔冬,刘英.动基座传递对准非线性滤波器的设计及应用[J].中国惯性技术学报,2010,18(1):33-37. Bao Q L,Sun S D,Liu Y.Design and application of nonlinear Kalman flter in moving base alignment of inertial navigation systems[J].Journal of Chinese Inertial Technology,2010,18(1):33-37.(in Chinese)
[6]王虎,王解先,白贵霞,李浩军.改进的渐消卡尔曼滤波在GPS动态定位中的应用[J].同济大学学报:自然科学版,2011,39(1):124-128. Wang H,Wang J X,Bai G X,Li H J.An improved fading Kalman flter and its application to GPS kinematic positioning[J].Journal of Tongji University:Natural Science,2011,39(1):124-128.(in Chinese)
[7]Xu T L,Ge Q B,Feng X L,Wen C L.Strong tracking flter with bandwidth constraint for sensor networks[C]//IEEE International Conference on Control and Automation,Xiamen,China:2010,596-601.
[8]Liu Z B,Shi Z Y,Xu W L.Multi-component information-equalized extended strong tracking flter for global localization:a scheme robust to kidnapping and symmetrical environments[J]. Robotics and Autonmous Systems,2010,58(5):465-487.
[9]Jwo D J,Wang S H.Adaptive fuzzy strong tracking extended Kalman fltering for GPS navigation[J].IEEE Sensors Journal,2007,7(5):778-789.
[10]Zhao S E,Li Y L.Multi-sensor information fusion and strong tracking flter for vehicle nonlinear state estimation[C]//IEEE Intelligent Vehicles Symposium,Xi'an,2009:747-751
[11]Xu W M,Kuang L L,Lu J H.Positioning algorithm with joint space-time constraints for unmanned network-flying vehicles[J].IEEE Transactions on Geoscience and Remote Sensing,2009,47(8):2694-2704.
[12]Xing J L,Ai H Z,Liu L W,Lao S H.Multiple player tracking in sports video:a dual-mode twoway Bayesian inference approach with progressive observation modeling[J].IEEE Transactions on Image Processing,2011,20(6):1652-1667.
[13]YesTe O A,Grajal J.Adaptive-fresh flters for compensation of cycle-frequency errors[J]. IEEE Transactions on Signal Processing,2011,52(1):1-10.
[14]BenesTy J,Paleologu C,Ciochina S.On regularization in adaptive fltering[J].IEEE Transactions on Audio,Speech,and Language Processing,2011,19(6):1734-1742.
[15]邓自立,王建国.非线性系统的自适应推广的Kalman滤波[J].自动化学报,1987,13(5):375-379. Deng Z L,Wang J G.Adaptive extended Kalman fltering for nonlinear systems[J].Acta Automatica Sinica,1987,13(5):375-379.(in Chinese)
(编辑:秦巍)
An Improved Strong Tracking Filtering Algorithm
QIAN Hua-ming1,GE Lei1,2,HUANG Wei1
1.College of Automation,Harbin Engineering University,Harbin 150001,China 2.706 Institute,The Second Academy of China Aerospace Science&Industry Corp,Beijing 100854,China
Strong tracking fltering(STF)sets small threshold to judge fltering divergence leading to fading factor with high probability,which causes excessive regulation of the fltering gain and makes the state estimation curve lack smoothness.By analyzing the operation mechanism of STF,improved STF(ISTF)is proposed.The proposed algorithm reduces probability of misjudging flter divergence by appropriately increasing the threshold.It determines the softening factor to suit diferent dimensions of the measurement equation,and thus avoids the disadvantages of the previous methods that determine the softening factor according to experiences.Simulation indicates that ISTF can maintain fltering accuracy and estimation smoothness,and is robust against sudden changes in the system state,showing its feasibility and efectiveness.
strong tracking fltering(STF),robustness,fading factor,softening factor
V556
0255-8297(2015)01-0032-09
10.3969/j.issn.0255-8297.2015.01.004
2012-07-06;
2012-12-27
国家自然科学基金(No.61104036)资助
钱华明,教授,博导,研究方向:组合导航、智能故障诊断和容错、信息融合、传感器技术及智能系统,E-mail:qianhuam@sina.com

