副车架侧边纵梁耐撞性优化设计

杨济匡　华长星　肖　志

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

副车架侧边纵梁耐撞性优化设计

杨济匡华长星肖志

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

为了对全框式副车架侧边纵梁结构进行耐撞性优化设计，以副车架侧边纵梁结构参数为变量，建立了该结构耐撞性和轻量化优化问题的数学模型。运用方差分析法(ANOVA)选择对副车架侧边纵梁耐撞性和轻量化影响显著的结构因子作为主要设计变量，采用正交试验设计方法进行试验设计；运用LS-dyna软件进行碰撞模拟；根据有限元仿真结果建立了响应面近似模型，并对该近似模型解决该问题的可靠性进行了验证，结果表明，所建立的响应面近似模型适合解决组合优化问题。优化设计后的副车架侧边纵梁能在提高耐撞性能的同时，保持较好的轻量化水平。

全框式副车架；方差分析；近似模型；优化设计

0　引言

为了达到对车内乘员进行保护的目的，一般要求在正面碰撞中车辆前部结构具有良好的吸能特性，车辆前部结构对乘员舱的侵入较小，并且要求车辆的碰撞加速度峰值越小越好。但目前的研究表明，在不改变原结构形式的条件下难以同时满足上述要求，如文献[1]中前纵梁采用加强板及蜂窝铝结构，虽然吸能量增加，但却导致碰撞峰值力显著增大，从而使得车辆前部对乘员舱的侵入变大。

在汽车前部结构中采用全框式副车架可以克服上述不足。通过合理设计其侧边纵梁，能够在汽车发生碰撞时，吸收较多的碰撞能量，同时增加一条传递碰撞力的途径，可有效地减小前纵梁对防火墙的侵入变形量。另外，全框式副车架有助于减小碰撞加速度峰值[2]。

为了提高某型轿车的耐撞性能，将其副车架设计成全框式结构，侧边纵梁采用S形薄壁梁结构。以有限元分析计算为基础，对副车架侧边纵梁耐撞性的结构参数进行了优化设计分析。

1　副车架侧边纵梁耐撞性优化设计

全框式副车架结构如图1所示。

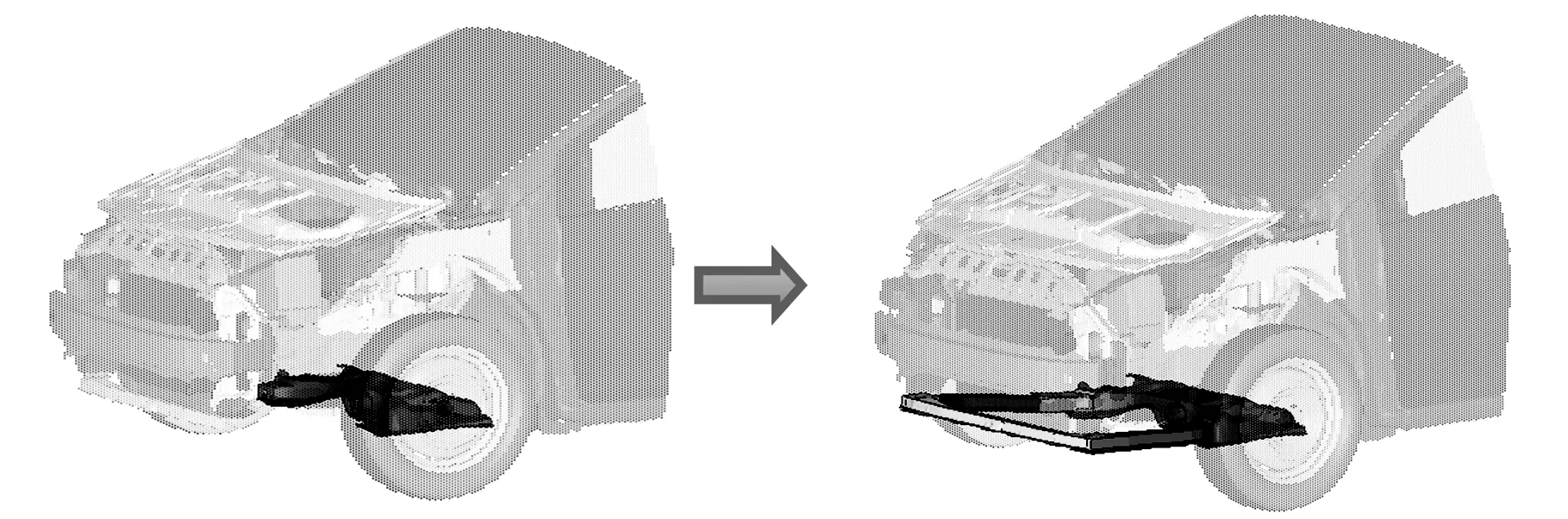
图1　全框式副车架结构

1.1副车架侧边纵梁设计分析

在碰撞过程中，侧边纵梁是副车架中参与吸收碰撞能量的主要结构件，因此对该段S形薄壁结构进行耐撞性的优化设计[3]。图2为副车架侧边纵梁结构主要设计参数和尺寸图。

(a)左视图

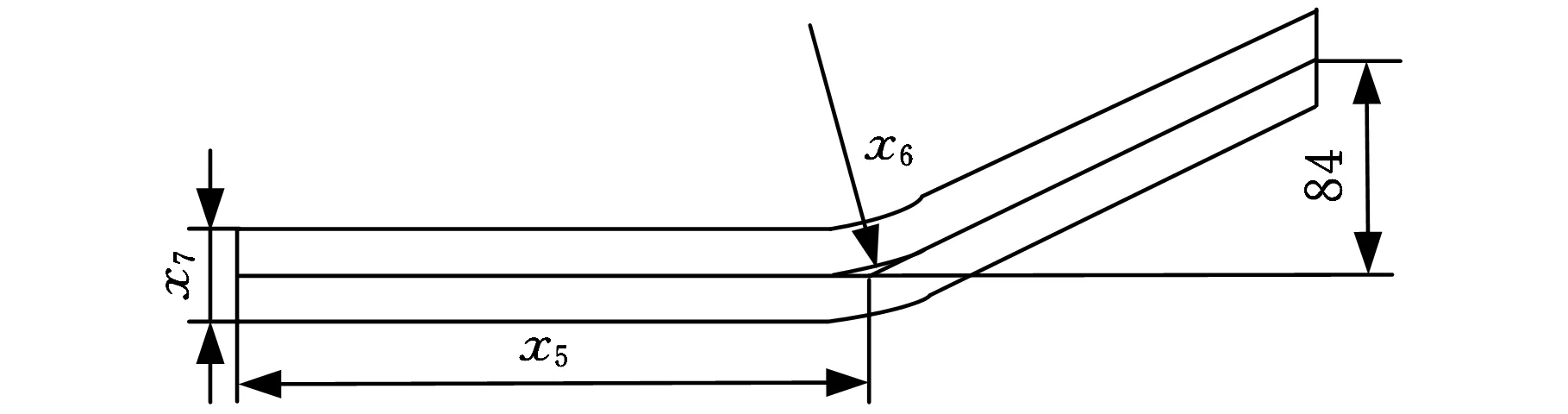
(b)俯视图图2　副车架侧边纵梁结构尺寸示意图

结构设计总长为532 mm；左视图中，两中心轴线的高度相差36 mm；俯视图中，侧边梁末端中心轴线与前端水平中心轴线距离相差84 mm。固定以上3个结构参数，可以保证侧边纵梁与副车架的连接关系不受其他尺寸参数的影响。其他主要结构参数尺寸如下：长度尺寸x1、x5；弯曲圆角x2；弯曲半径x3、x4、x6；界面宽度x7；界面高度x8。依据以上结构参数可以确定侧边纵梁的结构，设计优化模型的变量为

X=(x1，x2，x3，x4，x5，x6，x7，x8)

(1)

副车架侧边纵梁在碰撞时吸能越多，则副车架对于提高安全性的作用越大。侧边纵梁的质量是影响副车架轻量化性能的一个重要因子，要求在保证耐撞性能较好的同时使得结构的质量最小。因此，本文采用比吸能(specificenergyabsorption，SEA)进行考察[4]，比吸能越大则结构的耐撞性能与轻量化性能越好。比吸能ESA为

ESA=E/M

(2)

式中，E为结构吸能总和；M为结构总质量。

则基于耐撞性的副车架侧边纵梁结构参数组合优化数学模型表达如下：

(3)

式中，XL、XU分别为设计变量的下限值和上限值。

1.2副车架侧边纵梁有限元模型的建立

将副车架侧边纵梁CAD模型以igs格式导入Hypermesh软件中划分网格。整个模型采用3节点和4节点的壳单元，单元大小为5mm,沿单元厚度方向定义3个积分点。有限元模型如图3所示，副车架侧边纵梁的后端完全固定，前端设置一个仅保留轴向自由度的刚性板。刚性板沿轴向以10m/s的恒定速度使模型压溃160mm，模拟整车碰撞中侧边纵梁向后压缩变形量。侧边纵梁采用DP500高强钢材料，弹性模量为210GPa，泊松比为0.3，密度为7.85×103kg/m3，薄壁厚度为1.8mm。

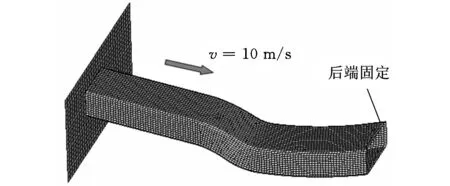
图3　副车架侧边纵梁简化构件有限元模型

2　副车架侧边纵梁优化过程

2.1试验设计

采用正交试验设计的方法来进行试验。考虑到侧边纵梁与副车架其他部件的连接关系，各结构参数变量的取值应当保证副车架侧边纵梁的连接位置不变。正交试验各因素水平的取值见表1。试验指标为副车架侧边纵梁的比吸能值。

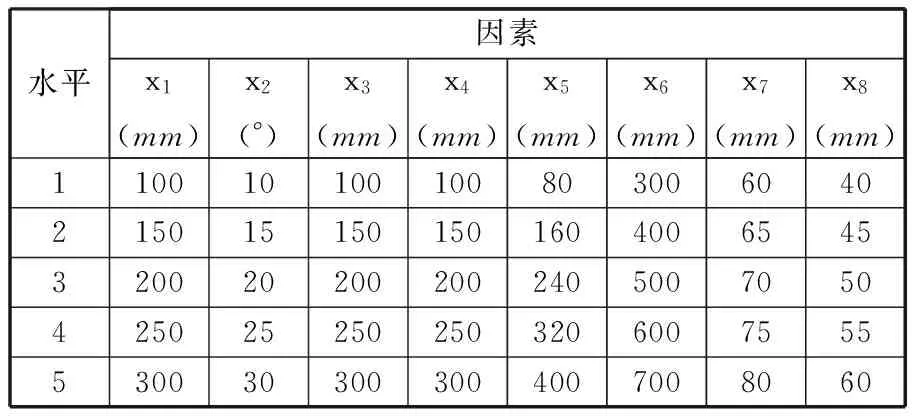
表1　副车架侧边纵梁各因素的水平取值

在副车架侧边纵梁的设计域内按照正交试验表L50(511)选择了50组样本点，对照每组样本点的结构尺寸，进行CAD建模、网格划分等一系列工作，建立碰撞试验模型，运用LS-dyna软件进行碰撞模拟计算，得到各样本点的比吸能值，如图4所示。

图4　比吸能试验结果

2.2因素显著性分析

利用方差分析法，评价副车架侧边纵梁结构参数对其耐撞性能影响的显著性[5]，剔除影响较小的结构参数，从而减少近似模型的因子数，使得在不需要增加样本点的同时，提高近似模型的可信度。

假设用正交表安排N个因素的正交试验，试验总次数为n，试验结果(试验指标)分别为x1,x2,…,xn。假定每个因素取m个水平，每个水平做p次试验，则n=mp。正交试验的方差分析步骤如下[6]。

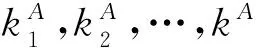
所有试验次数的平均值为

(4)

则因素A的组间离差平方和为

(5)

其他因素组间离差平方和类似于因素A的计算。

总离差平方和为

(6)

总离差方平方和可以分解成各因素组间离差平方和与误差平方和之和。即

ST=SA+SB+…+SN+SE

(7)

其中，SE为误差平方和。

(2)计算自由度。试验的总自由度为

fT=n-1

(8)

各因素自由度为

fF=m-1

(9)

试验误差的自由度为

fE=fT-NfF

(10)

(3)计算均方差平方和。记各因素的平均方差和为

MSF=SA/fF

(11)

试验误差的平均方差和为

MSE=SE/fE

(12)

最后将各因素的均方差平方和与误差的平均方差和相比，得到统计量F值。这个比值的大小反映了各因素对试验结果影响程度的大小。F值为

F=MSF/MSE

(13)

本文正交试验中，各因素均设计了5个水平数，所以由式(9)可知，各因数自由度均为

fF=m-1=5-1=4

(14)

本次仿真共进行了50次试验，利用式(8)、式(10)计算出试验误差的自由度为

fE=fT-NfF=50-1-8×4=17

(15)

首先运用前文所述方差分析式(5)～式(7)分别计算各因素的组间离差平方和、总离差平方和与误差平方和。限于篇幅，此处不赘述计算过程。然后利用式(11)～式(13)计算各因素的平均方差和MSF以及试验误差平均方差和MSE。最后得到各因素的统计量F，以上步骤可以采用SPSS软件分析得到[7]，结果见表2。

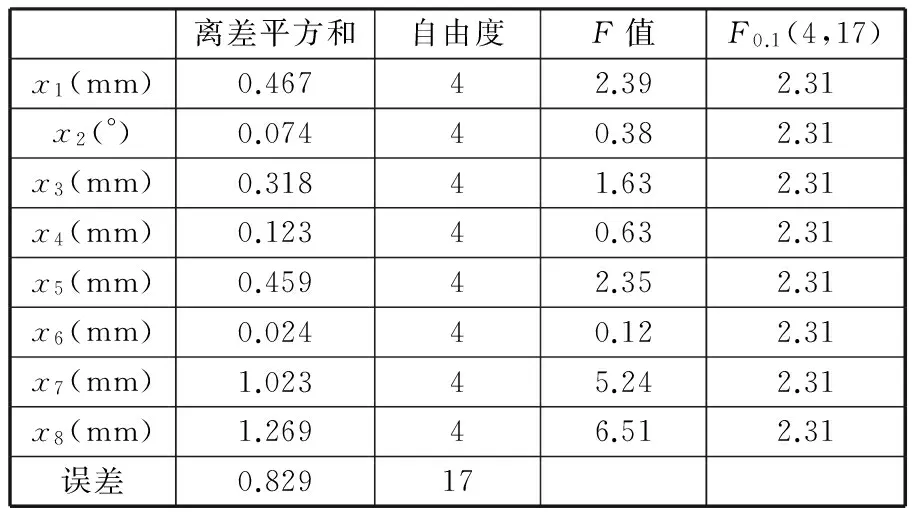
表2　各因素F值

从表2可以看出，因素x1、x5、x7、x8的变化对副车架侧边纵梁的比吸能值有显著影响。其中x7、x8的F值大于F0.01(4,17)=4.67，x7、x8为副车架侧边纵梁的截面尺寸，这说明副车架侧边纵梁的截面尺寸对其比吸能的影响十分显著，稍微改变即引起指标的很大变化。

因素x2、x3、x4、x6的变化对副车架侧边纵梁的比吸能值影响很小，将其定为常数[8]，取其值为比吸能值最大时所在的水平值，即x2=30°，x3=150 mm，x4=100 mm，x6=500 mm。

2.3响应面模型的建立

对新选出的4个因素重新安排试验，选用正交试验表L25(56)来安排试验。4个因素水平的取值仍按照表1中原有的数据进行。试验结果见表3。

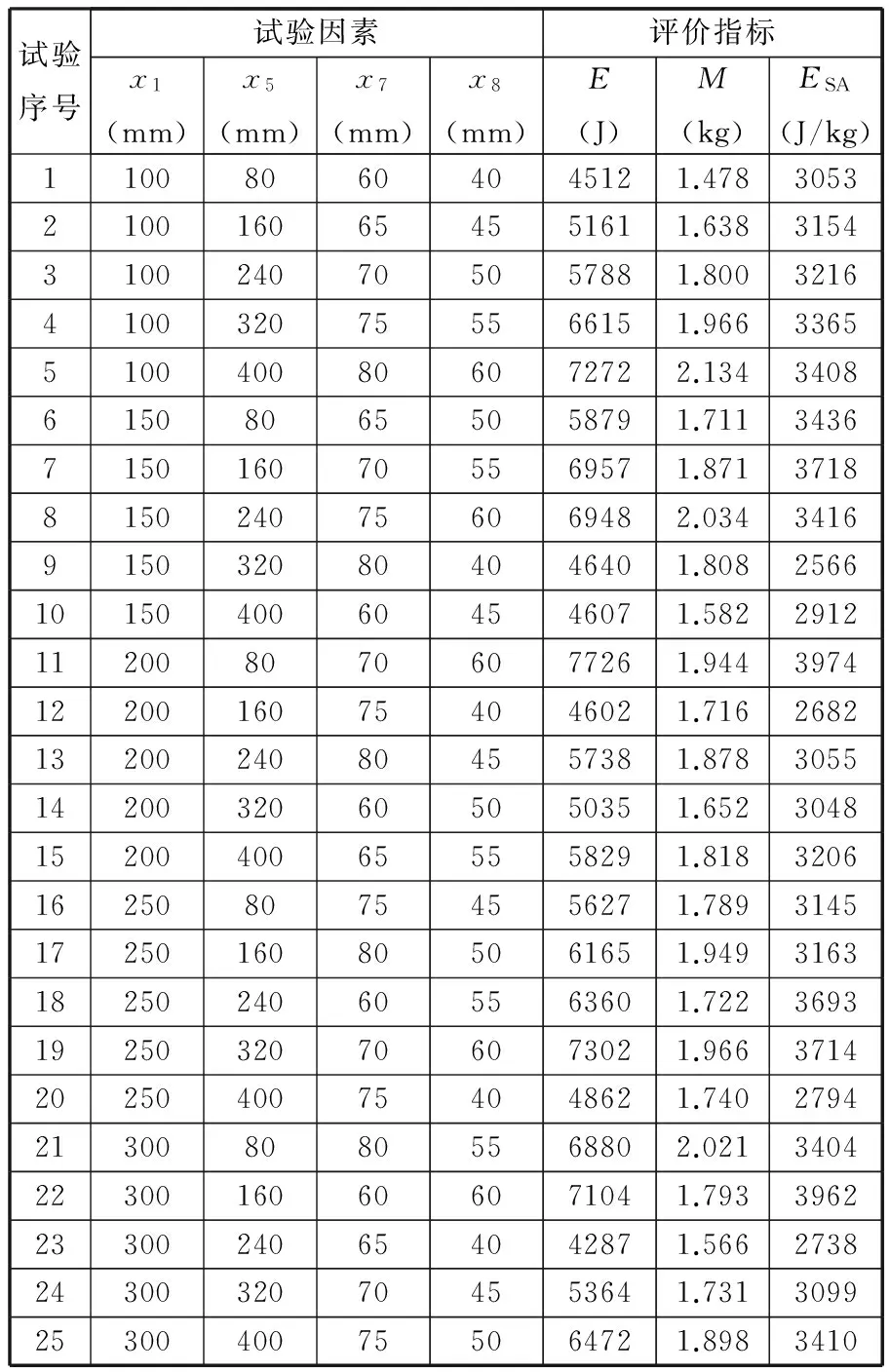
表3　四因素正交试验结果

根据试验结果并结合响应面方法[9]建立副车架侧边纵梁总吸能、质量以及比吸能的响应面模型。其方程如下：E=-13 514+3.5192x1-19.045 18x5+358.547 25x7+192.755 99x8-0.015 98x1x5-0.0367x1x7+

0.365 812x1x8+0.401 75x5x7-0.122 83x5x8+

(17)

M=-0.100 98+3.436 37×10-5x1-9.437 31×

10-5x5+0.016 52x7+0.015 356x8-6.987 69×

10-8x1x5-1.412 41×10-7x1x7+7.116 11×

10-7x1x8+1.547 42×10-6x5x7+7.355 08×

10-7x5x8+1.122 22×10-5x7x8-9.044 31×

(18)

ESA=-4795-0.3994x1-11.008 76x5+

148.846 21x7+146.746 13x8-0.008 39x1x5+

0.021 26x1x7+0.162 62x1x8+0.221 57x5x7-

(19)

采用方差分析的方法来考察所建立响应面模型的拟合精度。本文中E、M和ESA的响应面模型多重拟合系数分别为0.977、1.0、0.951。可见所建立的响应面模型的拟合精度较高。

2.4响应面模型预测值验证

为了进一步考察该模型对耐撞性问题的预测能力，利用多目标遗传算法NSGAⅡ对模型进行求解，得到总吸能、质量和比吸能的Pareto解集[10]。从Pareto解集中随机挑选5组解用于预测验证，根据挑选解提供的变量设置方案建立副车架侧边纵梁结构有限元模型并提交计算，得到有限元计算结果，将其与遗传算法的Pareto预测值进行比较，对比情况见表4。

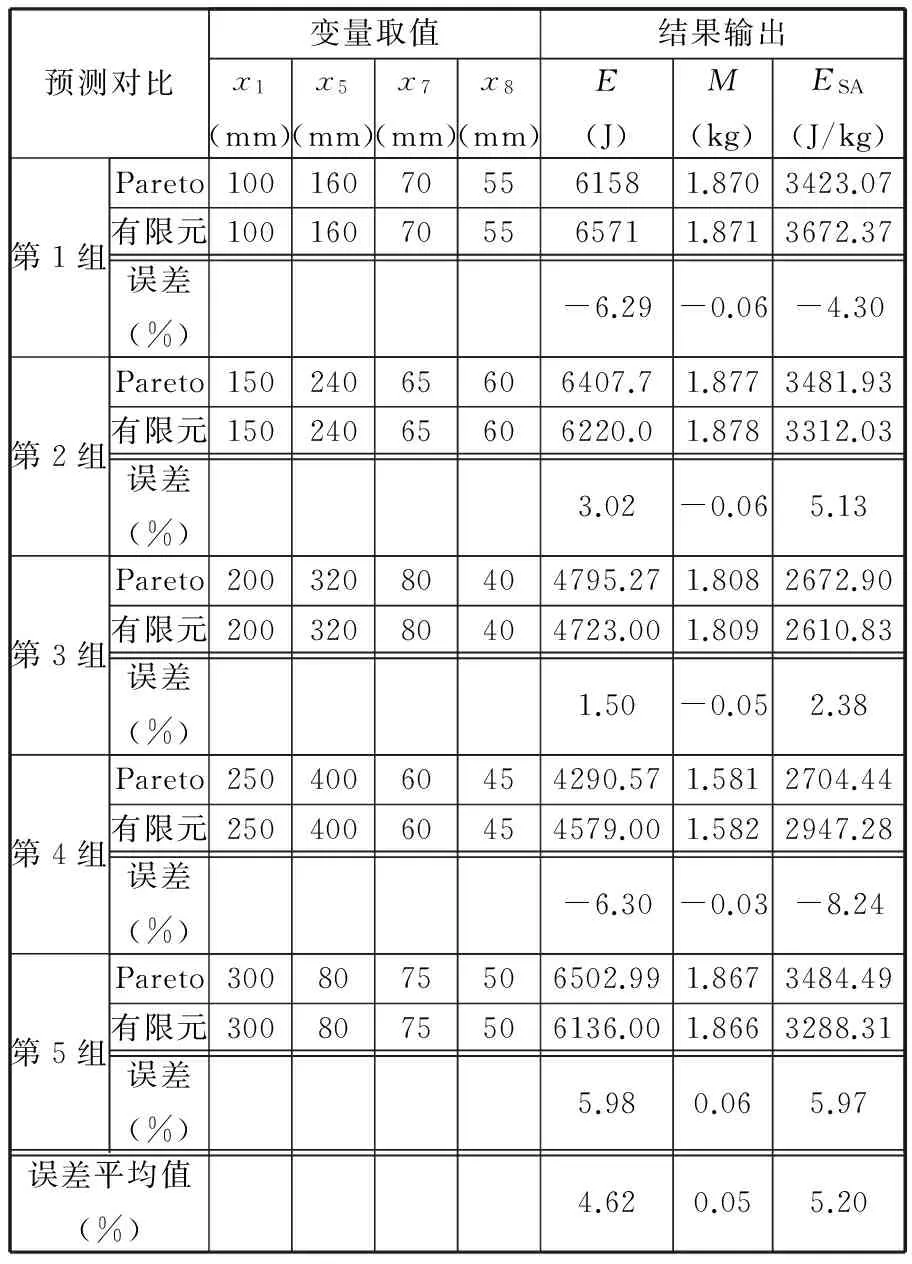
表4　响应面模型Pareto预测解与有限元仿真值对比验证

从表4可以看出，用于预测的5组预测解的E、M和ESA的响应平均误差分别为4.62%、0.05%和5.2%。各项指标的误差都控制在10%以内，这说明本文建立的响应面近似模型能够用于预测优化解。

2.5最佳优化结果验证

运用上文建立的响应面模型对式(3)表述的优化问题进行优化求解。优化得到的各参数值见表5。对优化后的副车架侧边纵梁进行有限元碰撞仿真分析，并将获得的结果与响应面模型的优化结果进行对比，见表5。

表5　优化后副车架侧边纵梁ESA值

由对比结果知，ESA优化解与有限元模拟计算结果之间的误差仅为6.85%，这进一步验证了近似模型的可靠性。优化后的副车架侧边纵梁耐撞性能和轻量化性能达到了一个较好的水平。

3　整车仿真分析

为了验证优化设计结果在整车碰撞过程中的可靠性，将副车架侧边纵梁的优化设计方案运用到整车中，进行正面100%刚性壁碰撞仿真分析。本文使用的整车模型已依据美国FMVSS 208碰撞测试标准进行了试验验证。图5和图6分别为实车试验时测得的后排座椅左右侧加速度曲线与仿真试验测得的加速度曲线对比图，由图可知，测量点的加速度变化趋势与实车对应点基本一致，由此证明该整车有限元模型可信，可用于后续仿真分析工作。

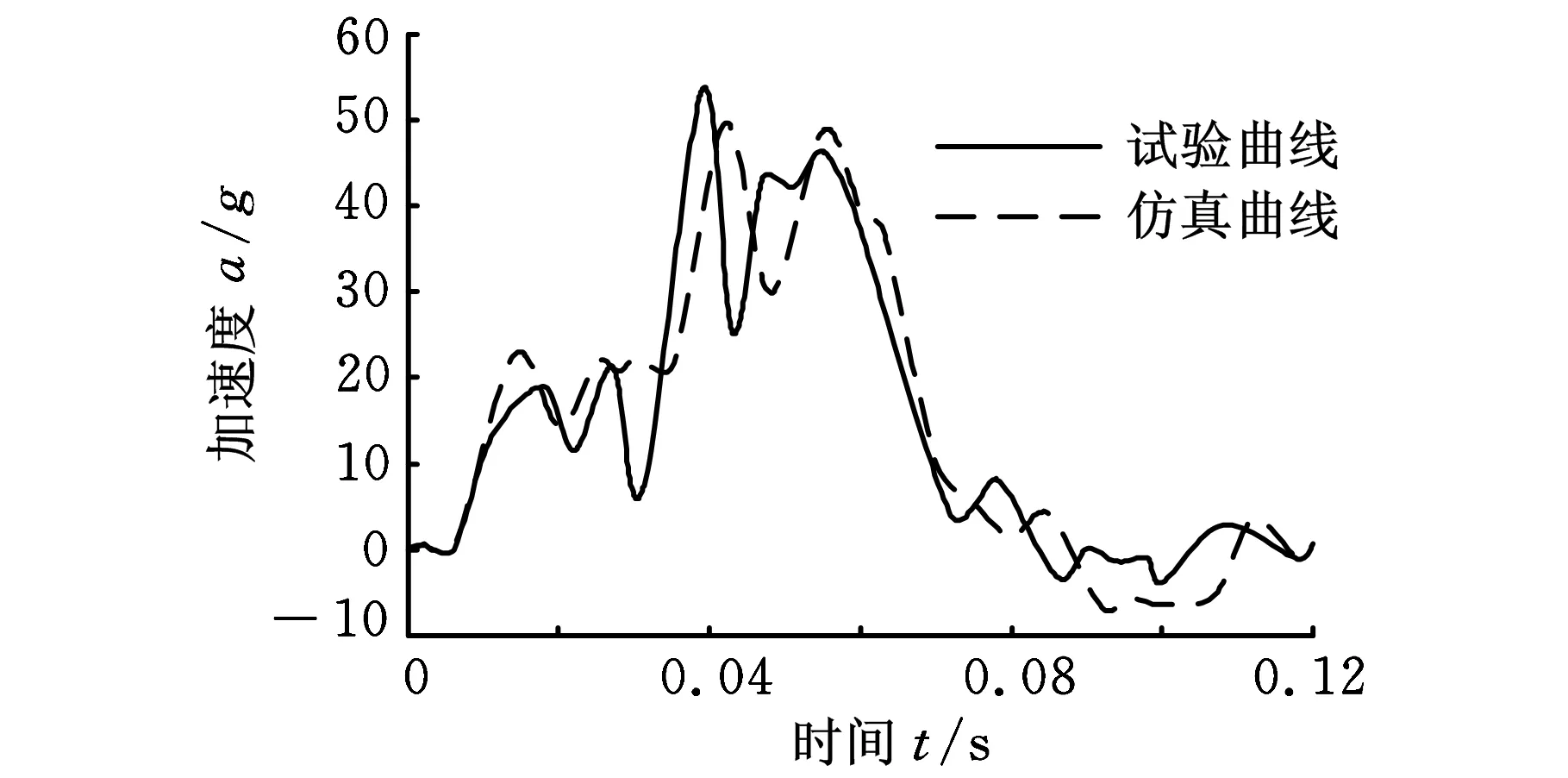
图5　后排座椅左侧加速度

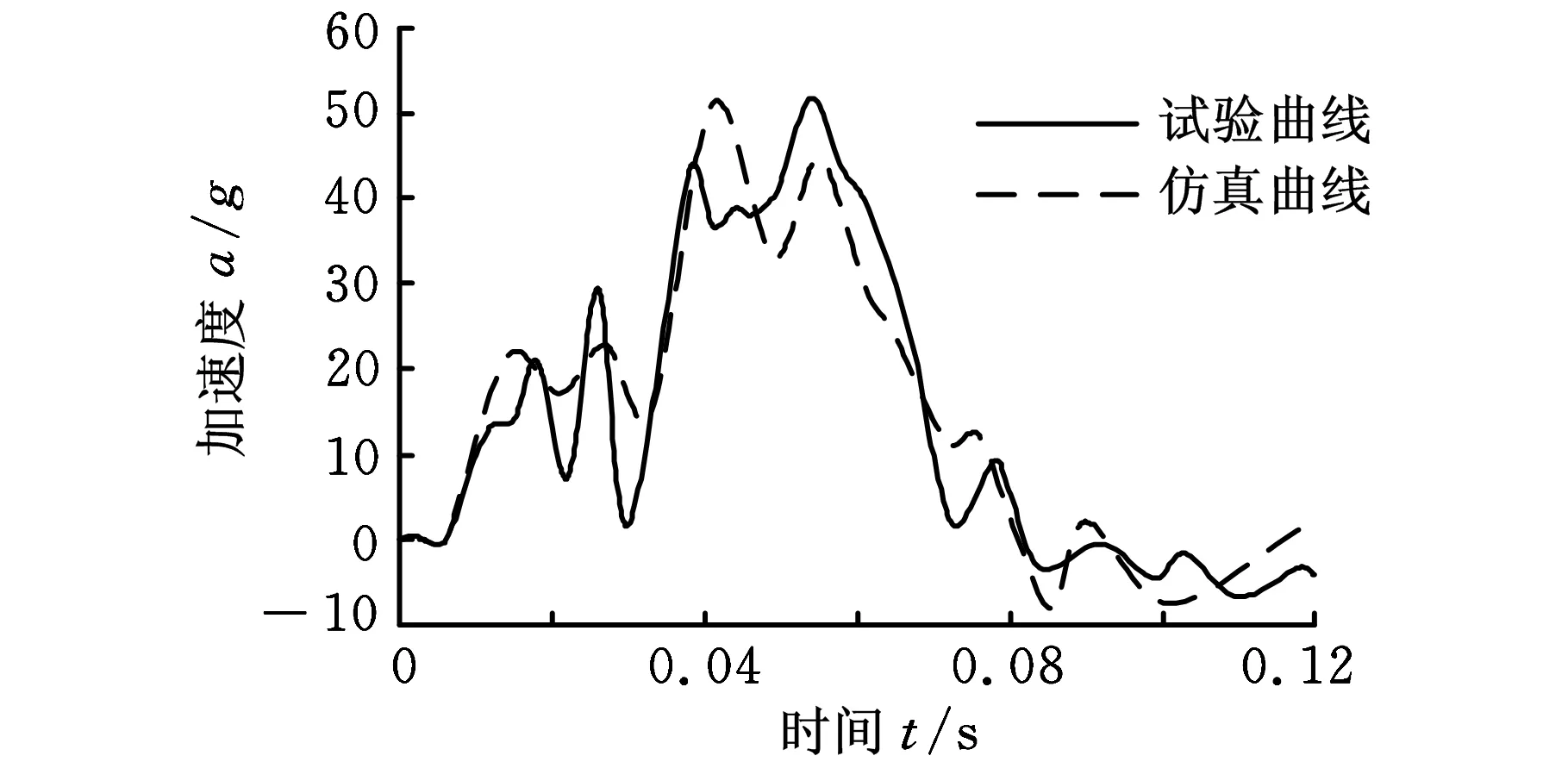
图6　后排座椅右侧加速度

本文按照新车评价规程2011版C-NCAP的要求进行整车在50 km/h速度下与固定刚性壁障100%重叠率正面碰撞仿真分析。将经过优化设计的结构运用到整车正面100%刚性壁碰撞中，由于采用全框式副车架结构，故整车的耐撞性得到了提高。副车架侧边纵梁在整车碰撞过程中吸收了13.8 kJ的碰撞能量，如图7所示，总质量为3.707 kg，可得其比吸能值为3722.8 J/kg。

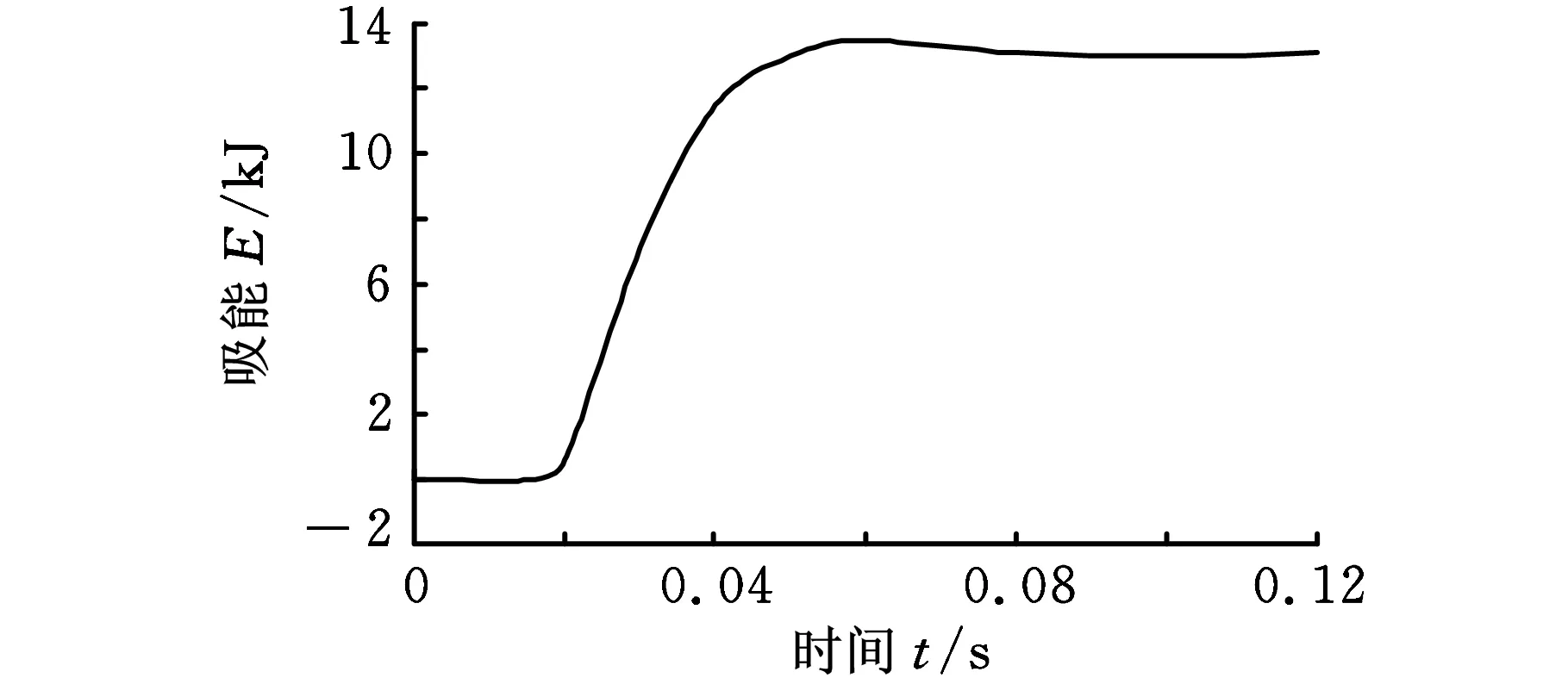
图7　整车碰撞中副车架侧边纵梁吸能图

图8所示为将副车架侧边纵梁优化设计方案运用在整车中的变形模式图与其未运用在整车中的变形模式图的对比。从图8可以看出，两者变形模式基本相同，这说明副车架侧边纵梁优化设计结果可信。

(a)副车架侧边纵梁在整车碰撞过程中的变形模式图

(b)副车架侧边纵梁简化模型中的变形模式图图8　副车架侧边纵梁变形模式对比

在碰撞过程中，采用全框式副车架能够提升吸收碰撞能量的能力，从而使得整车耐撞性能得到提升。图9所示为副车架改进前后防火墙向乘员舱侵入量的对比。从图9可以看出，改进前防火墙的侵入量较大，最大侵入量达到了191.4 mm；改进后防火墙的侵入量明显减小，最大侵入量仅为143.3 mm。

图10所示为副车架改进前后左右两侧B柱加速度大小的对比。从图10a可以看出，改进前左侧B柱加速度为37.6g，改进后为34.3g。图10b表明改进前右侧B柱加速度为39.6g，改进后为31.9g。

(a)改进前防火墙侵入量

(b)改进后防火墙侵入量图9　副车架改进前后防火墙侵入量对比

(a)改进前后左侧B柱加速度对比

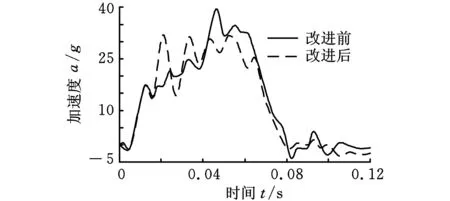
(b)改进前后右侧B柱加速度对比图10　副车架改进前后左、右侧B柱加速度对比

4　结论

(1)通过试验设计，用方差分析的方法得到副车架侧边纵梁4个对其吸能和轻量化性能有显著影响的结构参数。

(2)以影响较为显著的4个结构参数为研究对象，重新进行试验设计。建立了副车架侧边纵梁总吸能量和质量的响应面模型，并对模型的精度和可信度进行了验证。

(3)利用响应面模型对副车架侧边纵梁进行了优化设计，并将优化结果代入整车模型进行仿真，得到整车碰撞中副车架侧边纵梁的变形模式与其简化模型中的变形模型相同的结论，从而验证了优化设计结果的准确性。

(4)采用全框式副车架及优化侧边纵梁后，防火墙向乘员舱侵入量减小25%，整车耐撞性性能有了较大的提高。

[1]Zhang C，Saigal A.Crash Behavior of a 3D S-shape Space Frame Structure[J].Journal of Materials Processing Technology，2007，191(1/3)：256-259．

[2]Tian Xin，Chen Gan，Shi Jianpeng．The FM Simulation of Structure Improvement of a Car Subframe[J].Automotive Technology，2009(5):1.

[3]Hou Shujuan．Design Optimization of Thin-walled Components with Crashworthiness Criteria[D].Changsha：Hunan University, 2007．

[4]施颐，朱平，张宇，等．基于刚度与耐撞性要求的车身结构轻量化研究[J]．汽车工程，2010，32(9)：757-762．

Shi Yi,Zhu Ping,Zhang Yu,et al.A Study on the Lightweighting of Car Body Structure Based on Stiffness and Crashworthiness Requirements[J].Automotive Engineering, 2010，32( 9)：757-762.

[5]Liu Minglei.Variance Analysis of Orthogonal Experimental Design[D].Harbin：Northeast Forestry University，2011.

[6]Chen Kui.Design of Experiment and Analysis[M]．Beijing：Tsinghua University Press，2005．

[7]Gao Zhongjiang，Shi Shuliang，Li Yu.Application of SPSS in ANOVA of Biological Statistics[J]．Progress in Modern Biomedicine，2008,11(8)：2116-2120.

[8]Wu Hequan, Xin Yong, Hu Hongwei.Parameters Optimization of S-shaped Rail for Crashworthiness Analysis[J].Journal of Highway and Transportation Research and Development，2009,26(12)：131-136.

[9]Khoo L P，Chen C H．Integration of Response Surface Methodology with Genetic Algorithms [J]．International Journal of Advanced Manufacturing Technology，2001，18(7)：483-489.

[10]Chen Jiqing，Huang Xinhong，Zhou Yunjiao，et al.Comparison of Crashworthiness Optimization Methods of Steel-Aluminum Hybrid Automotive Front Rail[J].Journal of South China University of Technology，2012，40(7)：90-94.

(编辑陈勇)

Optimization Design for Crashworthiness of Sub-frame Side Rails

Yang JikuangHua ChangxingXiao Zhi

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082

In order to optimize design of a whole box-type sub-frame side rails in terms of structural parameters to meet the requirements for light weight and crashworthiness in front impact,an optimization mathematical model was established in terms of design variables of the sub frame side rails. First, analysis of variance was carried out to choose the factors that had significant influences on the light weight and crashworthiness of sub-frame side rails as the main design variables. Secondly, a design test was conducted by using orthogonal experimental design method. Then, the Ls-dyna program was utilized for crash simulations. A response surface approximation model was built up according to the simulation results, and the approximate model was validated to solve the reliability problem. The results show that the model established by the response surface is suitable for solving the combined optimization problem in this study. The optimized sub-frame side rails can improve crashworthiness performance while maintain a good light-weight level.

whole box-type sub-frame side rail;analysis of variance;approximation model;optimization design

2013-09-09

国家高技术研究发展计划(863计划)资助项目(2006AA110101)；湖南大学汽车车身先进设计制造国家重点实验室自主研究项目(61075004)

U461.91DOI：10.3969/j.issn.1004-132X.2015.01.022

杨济匡，男，1948年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。主要研究方向为汽车安全、碰撞损伤生物力学。华长星，男，1989年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。肖志，男，1977年生。湖南大学汽车车身先进设计制造国家重点实验室讲师。