高墩自复位隔震机理

夏修身，陈兴冲，李建中



高墩自复位隔震机理

夏修身1，陈兴冲1，李建中2

(1. 兰州交通大学土木工程学院，甘肃兰州，730070；2. 同济大学土木工程学院，上海，200092)

为了探讨桩基础高墩自复位隔震机理，用2个弹簧模拟桥墩的提离摇摆，考虑限位钢筋的影响，基于某铁路高墩桥梁，采用非线性时程分析方法，输入3条强震记录，讨论高墩摇摆反应随提离弹簧刚度、基础宽度及参数变化的规律。研究结果表明：提离弹簧刚度越小桥墩的摇摆振动越剧烈、摇摆反应越大，墩顶位移随的增大而减小、有明显的线性关系，墩底弯矩随的变化相对复杂。通过基础宽度、及墩−承台的接触刚度调整均可以实现对桥墩摇摆反应的控制。

高墩；桩基础；自复位；隔震机理；反应控制

高墩相对较柔，强震作用下墩顶会产生较大位移，墩中还会形成2个以上的塑性铰区且塑性铰位置具有分散与不确定性[1−2]。常用的支座减、隔震装置及黏滞阻尼器等的位移适应能力较小[3−6]，不适用于高墩桥梁。规范中的延性抗震设计适用于潜在塑性铰位置明确的桥梁[7]，也不适用于高墩。鉴于高墩抗震及减、隔震设计中存在的问题，文献[8]提出了有自复位功能的桩基础高墩摇摆隔震装置，采用简化模型研究表明该装置有较好隔震效果。文献[9]建立了高墩提离摇摆的分布Winkler弹簧模型及两弹簧模型，给出了抗倾覆弯矩的计算公式。文献[10]对桩基础高墩摇摆隔震的3个分析模型进行了对比研究，指出了各模型的分析精度。文献[11]提出了限位钢筋的数值模拟方法，完善了桩基础高墩摇摆隔震的分析模型。已有研究表明，基础宽度及限位钢筋屈服力的变化都会引起抗倾覆弯矩的改变，其对桥墩自复位隔震机理的影响尚没有相关的研究。针对摇摆隔震分析模型中的提离弹簧刚度，文献[9]给出了取值原则，文献[10]给出了计算公式。提离弹簧刚度与桥墩下方的基础材料特性有关，其改变对摇摆反应的影响规律也缺少系统研究。本文作者基于提离弹簧接触刚度、基础宽度与参数变化对桩基础高墩摇摆反应的影响规律研究，探讨高墩的自复位隔震机理，为自复位隔震高墩摇摆反应的控制提供依据。

1 摇摆隔震装置及其分析模型

为了达到强震下既保护桥墩又保护基础的抗震目标，文献[8]提出了桩基础高墩摇摆隔震装置(见图1)。

(a) 黏着阶段；(b) 提离摇摆阶段

摇摆隔震装置通过竖向荷载(结构自重)平衡水平荷载(风、制动力及多遇地震作用)满足正常使用，此时按岩石地基上的扩大基础进行设计。强震下当墩底地震弯矩超过恒载等提供的抗倾覆弯矩时墩底的一侧相对于桩基础产生竖向的位移，发生提离(图1(b))。提离后绕另一侧摇摆，桥墩利用提离摇摆达到隔震目的，震后靠自重实现完全复位。为避免摇摆过程中墩顶产生较大位移，可通过钢筋限位。墩底的扩大基础通过局部配筋、黏角钢及倒角等细部构造措施可避免提离时由局部应力集中及承台与扩大基础的刚性碰撞造成墩底扩大基础严重损坏。

文献[9]和[10]建立了桩基础高墩摇摆隔震分析的两弹簧模型。文献[11]在两弹簧模型中考虑了限位钢筋的影响(见图2)，完善了桩基础高墩摇摆隔震分析模型。本文采用图2所示的模型进行参数敏感性分析。当限位装置的初始间隙取较大值时，即限位钢筋不起作用，模型此时退化为不考虑限位钢筋的两弹簧模型。

图2 考虑限位的两弹簧模型

模型中弹性梁单元模拟墩柱，集中质量模拟桥跨重，刚臂单元模拟承台及墩底扩大基础，基础质量堆积于扩大基础的重心，模型采用瑞利阻尼，提离弹簧只受压，刚度按下式近似计算[12]：

(2)

式中：v为竖向刚度；0为等效半径；0为墩底扩大基础的截面积；为承台材料的剪切模量；为承台材料的泊松比。

图2中限位单元初始刚度按下式计算[11]：

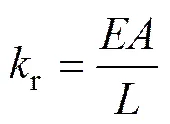
式中：为限位钢筋或钢铰线的弹性模量；为限位钢筋或钢铰线的截面积；为限位钢筋或钢铰线的非约束长度。

限位单元的滞回规则由3条加、卸载路径组成如下：

1) ①→②→③→④为从点至点及其以后的持续加载路径；

2) ③→⑤→⑥为从点的卸载点，再从点(或中的任一点)加载至路径；

3) ②→⑦为从点(或到之间的任一点)加载至点，再从点(或之间的任一点)卸载至点的路径。

2 基本分析数据

某单线铁路特大桥，上部结构为等跨布置32 m简支箱形梁，下部结构为圆端形空心高墩、群桩基础，桥型立面布置见图3。以58 m 高的18号桥墩为研究对象，隔震前18号顺桥向第1周期为0.95 s，墩底扩大基础长×宽×高为10 m×12 m×2 m。顺桥向隔震设计时墩底扩大基础为30混凝土、宽=10 m，扩大基础底的恒载竖向力为33 873 kN，截面积0=120 m2。

单位：m

从美国太平洋强震数据库(PEER)[13]选取了1940年Imperial Valley地震El-Centro记录为输入地震动(见图4)。为考察摇摆反应的离散性，还另外选取了1994年Northridge和1952年Kern County地震Taft记录。

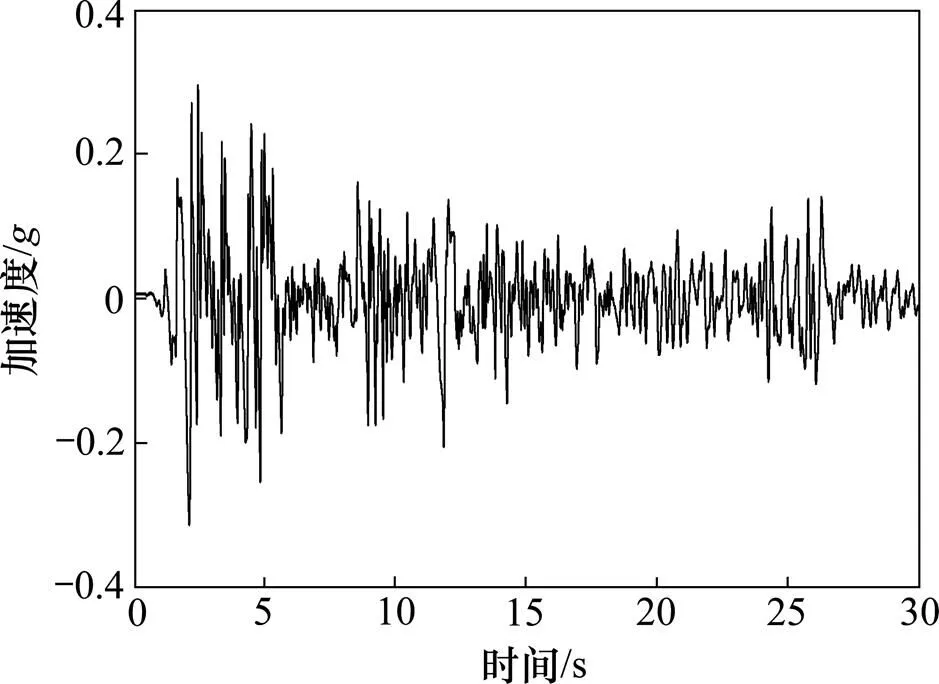
图4 El-centro强震记录

3 基础刚臂取值的影响分析

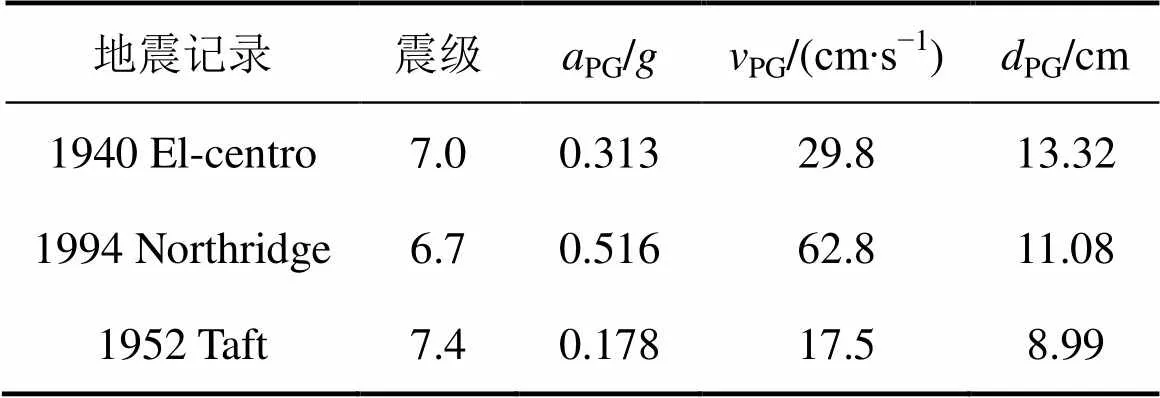
表1所示为3条强震记录的震级、地面峰值加速度(PG)、地面峰值速度(PG) 和地面峰值位移(PG)信息。3条地震波的加速度幅值统一调整到0.57，按顺桥向的水平方向输入，考虑到地震波30 s之后的加速度较小，只输入各地震波的前30 s。

表1 地震波信息

Table 1 Information pertinent to ground motions

文中=13 333 MPa，按式(1)得每端弹簧刚度= 2.1×108kN/m。不考虑限位钢筋的影响，取=10 cm。墩柱底部截面的抗弯刚度记作I，本文算例I=3.9×109kN∙m2。基础刚度用刚臂模拟，在有限元软件中通常取最大单元刚度的100倍以上，本文分析中其在100I~10 000I之间取值。

图5~7所示为El-centro波下桥墩的摇摆反应时程曲线。表2所示为3条强震记录下的摇摆反应峰值。

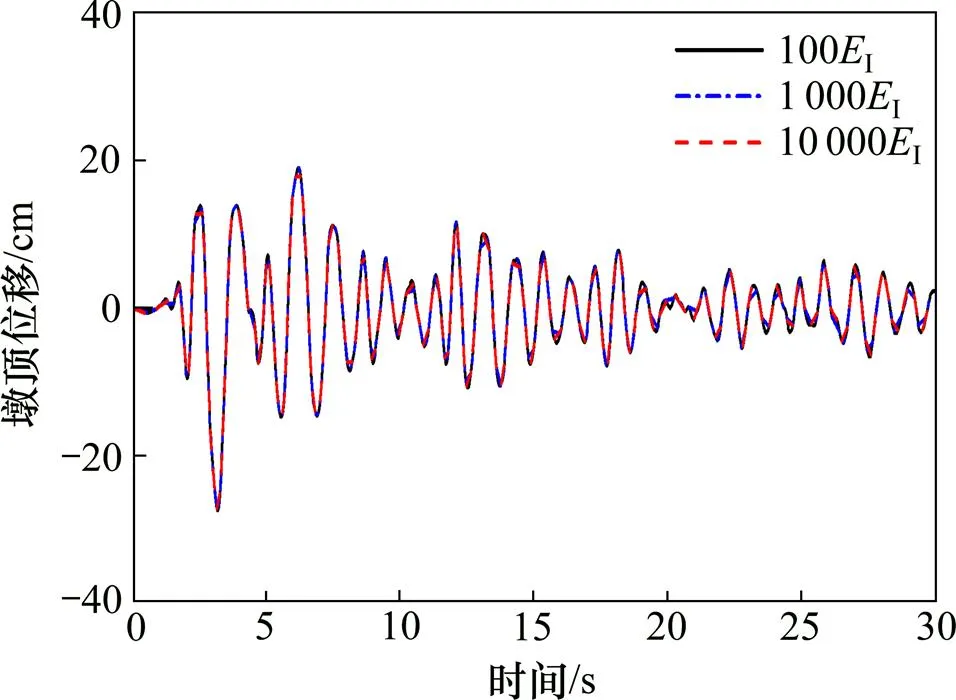
图5 不同刚臂的墩顶水平位移时程曲线比较(El-centro)

图6 桥墩扩大基础的提离位移比较(El-centro)

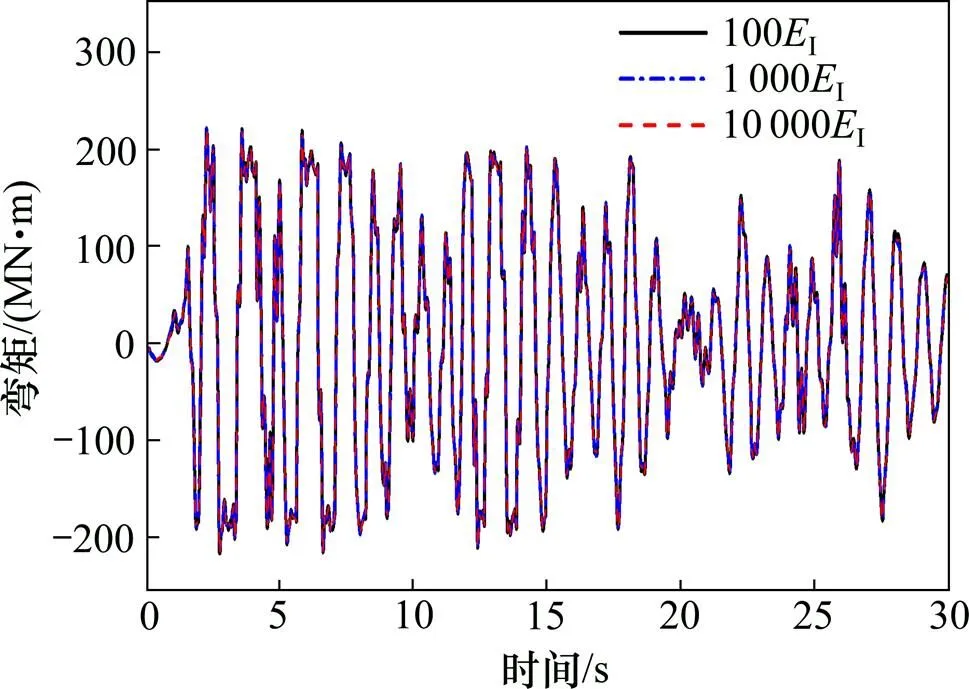
图7 不同刚臂的墩底弯矩时程曲线比较(El-centro)

表2 刚臂取值对摇摆反应的影响

Table 2 Influence of stiffness of rigid beam on rocking responses

由图5~7及表2可以看出：当基础刚臂在100I~ 10 000I之间取值时，墩顶位移、基础提离位移及墩底弯矩的反应峰值及时程曲线重合较好、受基础刚臂抗弯刚度的影响较小，即数值分析时对此参数的变化反映不敏感。以下分析中均取基础刚臂为100I。

4 提离弹簧刚度取值的影响分析

按式(1)可得，提离弹簧的刚度=2.1×108kN/m，其与桥墩所接触的基础材料剪切模量泊松比和等效半径0有关。当桥墩下方的基础材料发生变化时，提离弹性的刚度也会随发生变化。以下讨论弹簧刚度在2.1×107~2.1×1010kN/m之间取值时，桥墩的摇摆反应变化规律。等效半径不变情况下，弹簧刚度越大代表基础材料的剪切模量越大、泊松比越小，即材料越坚硬。

图8和图9及表3所示为El-centro波下弹簧刚度取值对桥墩摇摆反应的影响。

图8 不同提离弹簧刚度的墩顶水平位移时程曲线比较(El-centro)

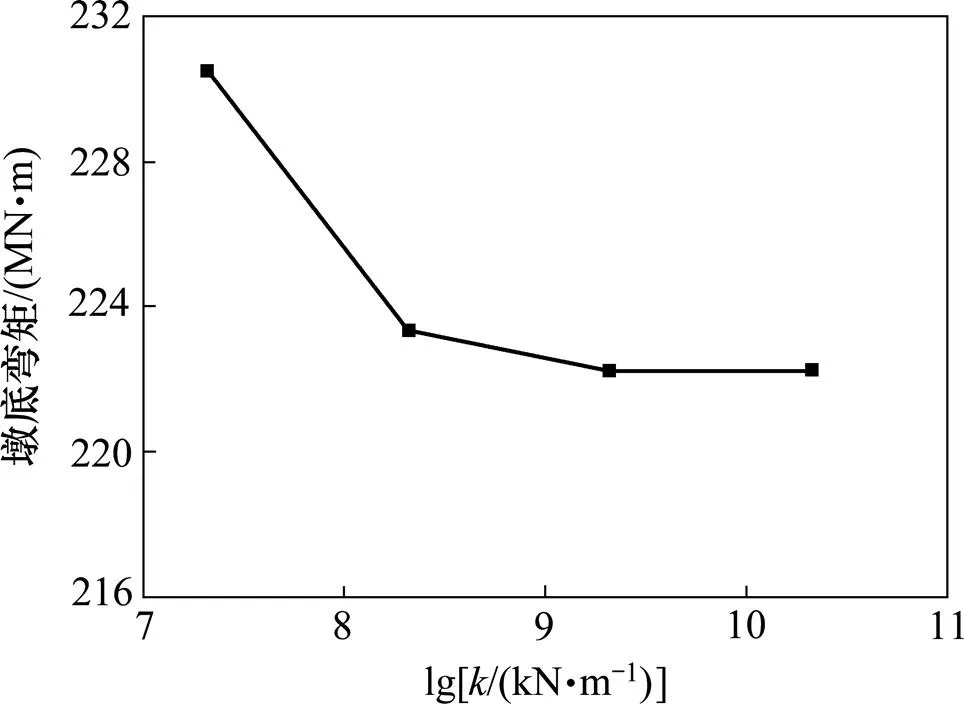
图9 弹簧刚度与墩底弯矩的关系(El-centro)

表3 提离弹簧刚度对摇摆反应的影响(El-centro)

Table 3 Influence of spring stiffness on rocking responses

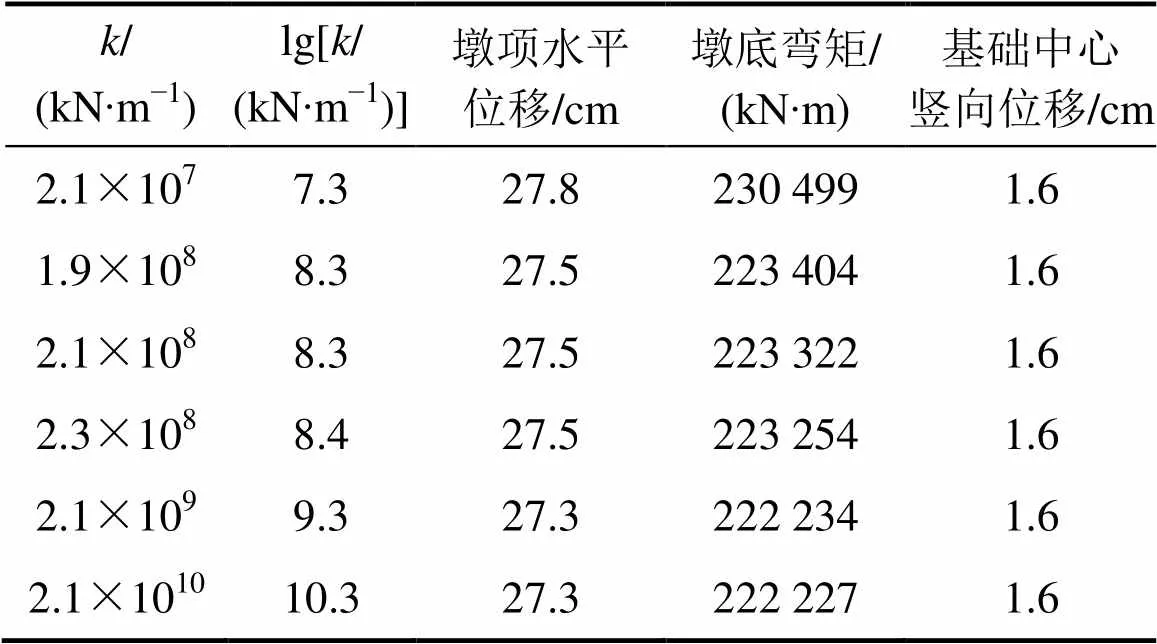
由表3可以看出：当弹簧刚度=2.1×108kN/m变化±10%，即弹簧刚度分别取2.3×108kN/m和 1.9×108kN/m时，若只考虑1位小数点则墩顶位移与基础中心的竖向位移无变化；而墩底弯矩则对应减小了0.03%和增大了0.04%。这表明，弹簧刚度变化10%时，对摇摆反应的影响极小。由表3还可以看出：基础中心的竖向位移为1.6 cm小于限位钢筋的初始间隙10 cm，表明满足前面不考虑限位钢筋的假定。

由图8可以看出：除最小提离弹簧刚度的时程曲线外，其余3个基本重合、但振动幅值不同，这表明弹簧刚度在1.9×108~2.1×1010kN/m之间变化时对桥墩摇摆振动周期特性影响很小，对摇摆振动的剧烈程度有一定的影响。由图9及表3可以看出：墩顶位移及墩底弯矩随着弹簧刚度的增大而减小，但当弹簧刚度增大到2.1×109kN/m以后，墩顶位移及墩底弯矩基本不变。弹簧刚度由2.1×107kN/m增加到2.1× 1010kN/m时，墩底弯矩由230 499 kN/m减小到222 227 kN/m减小了3.6%，墩顶位移减小了1.8%。Taft波与Northridge波下也有此规律，其结果没有单独列出。这是因为墩顶位移主要取决于桥墩自身弹性变形与提离转动引起的刚体位移。桥墩的水平弹性变形及刚体位移受提离弹簧承压刚度的影响主要表现在摇摆振动产生的桥墩水平弹性变形(有动力放大)及提离转动引起的刚体位移。提离弹簧刚度越小、桥墩的摇摆振动越剧烈，动力放大作用相对明显，体现为图8、图9及表3中的较大位移振幅及墩底弯矩。墩底弯矩主要由桥墩的提离摇摆条件决定，与桥墩的提离弹簧刚度有关是因为摇摆振动时引起的抗倾覆弯矩动力放大，所以，较小地提离弹簧刚度对其影响相对较大。总体来看，通过提离弹簧刚度的变化，即桥墩下承台材料特性的调整，可在一定程度上控制桥墩的摇摆反应。

5 抗倾覆弯矩变化的影响分析

5.1 基础宽度取值的影响

地震作用下，桩基础高墩提离摇摆产生的条件是墩底的地震弯矩大于由自重等提供的抗倾覆弯矩y。文献[8]提出了自重提供的抗倾覆弯矩计算公式如下：

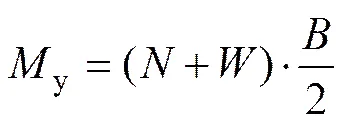
式中：为桥跨在墩顶的支反力；为墩身的自重；为与墩身相连的计算方向扩大基础宽。

由式(4)可知：竖向荷载(+)与计算方向的基础宽是抗倾覆弯矩y的2个决定因素。当基础宽度发生变化时，抗倾覆弯矩y也随之发生变化。为保证尺寸改变也满足正常使用，本节采取逐渐加大基础宽度的方法来改变抗倾覆弯矩，见表4。分析中，提离弹簧的刚度=2.1×108kN/m保持不变，限位钢筋的初始间隙与前节相同。模型中考虑承台尺寸改变引起的承台质量效应影响。

表4 基础宽度与其对应的关键参数

Table 4 Width of foundation and its corresponding key parameters

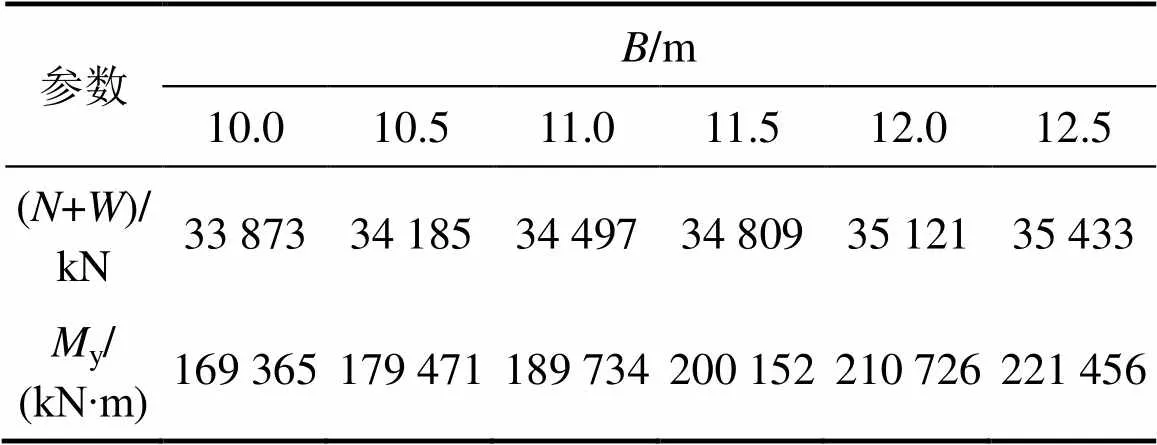
图10~13和表5所示为El-centro波下基础宽度的变化对桥墩摇摆反应的影响。

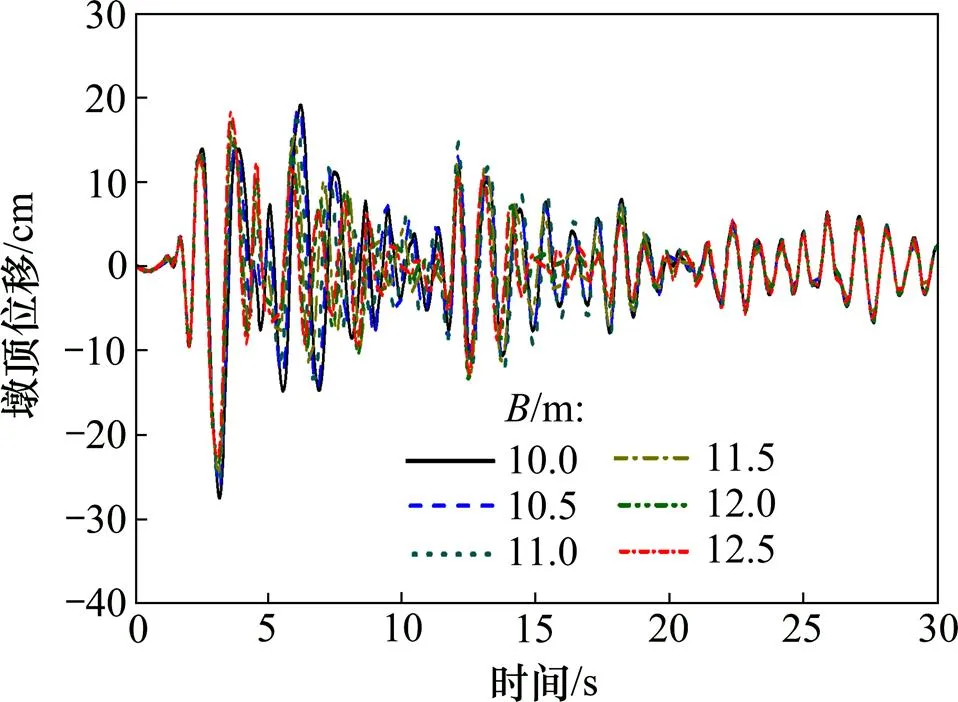
图10 不同基础宽度的墩顶水平位移时程曲线比较(El-centro)

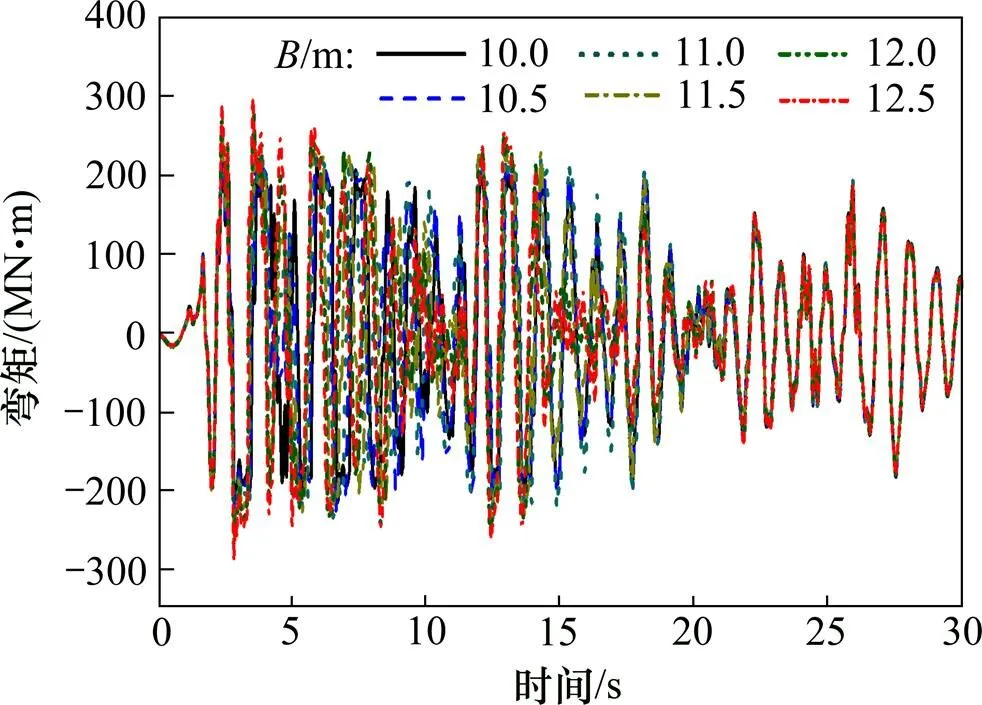
图11 不同基础宽度的墩底弯矩时程曲线比较(El-centro)

图12 基础宽度与墩顶位移的关系(El-centro)

图13 基础宽度与墩底弯矩的关系(El-centro)

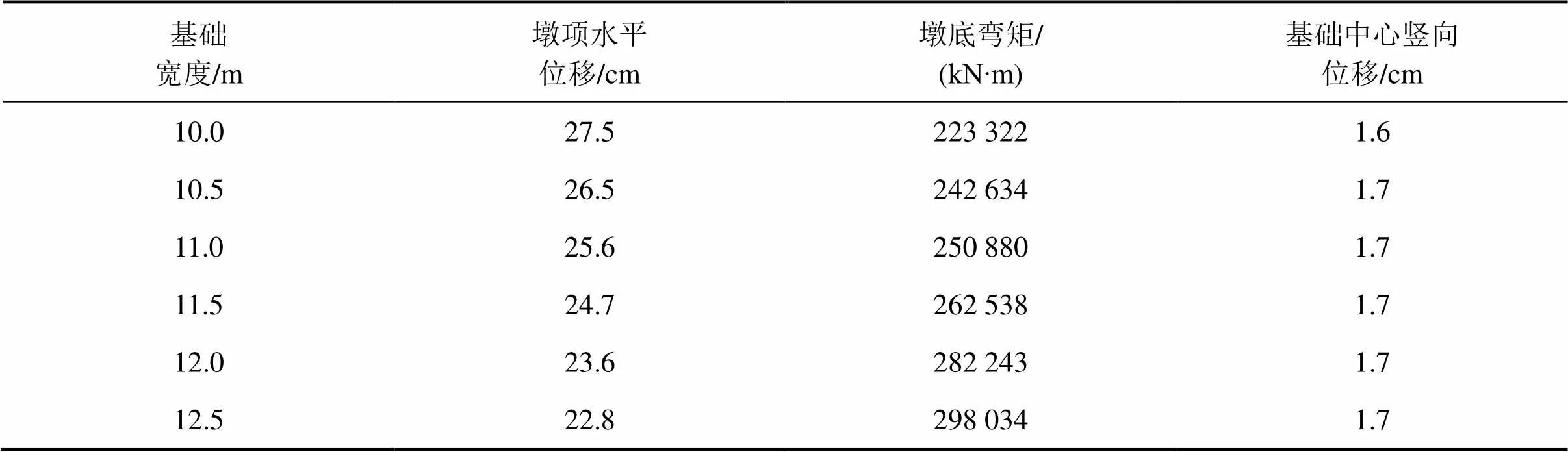
表5 基础宽度对摇摆反应的影响(El-centro)

Table 5 Influence ofon rocking responses

由图10和图11可以看出：随着基础宽度的变化，墩位移及墩底弯矩时程曲线也发生了变化。这是因为基础宽度的变化引起墩底抗倾覆弯矩发生变化，从而导致摇摆振动特性的改变，故反映在时程曲线上有幅值不同及波峰与波谷形状不重合。

由表5结合图12、图13可以看出：基础宽度越小、桥墩的摇摆振动越剧烈、墩顶位移越大。且有墩顶位移随基础宽度的增大而减小，墩底弯矩随基础宽度的增大而增大，近似呈线性关系，表明通过改变基础宽度可有效地控制桥墩的摇摆反应。其他2条波下也有此规律。图11及表5中，基础宽度越小、桥墩的摇摆振动越剧烈、但对应的墩底弯矩也越小，是因为墩底弯矩取决于2个因素：1) 决定提离摇摆抗倾覆弯矩y；2) 摇摆振动引起的y动力放大。y与基础宽度呈线性关系(见式(4))，而动力放大效应与摇摆振动的周期特性及地震波的频谱有关。由图10和图11可见：文中改变前后时程反应的曲线形状改变较小，表明改变前后的y动力放大效应基本一致。故动力放大效应对墩底弯矩的影响弱于的改变，这也是呈近似呈线性关系的原因。

5.2变化的影响分析

前面的分析表明：抗倾覆弯矩y(与基础宽度呈一一对应)的改变对桥墩的摇摆振动及摇摆反应有较大的影响。而图1中的限位钢筋有些情况下也会增大桥墩的抗倾覆弯矩[11]，其提供的抗倾覆弯矩记为r，见式(6)。为研究由限位钢筋引起的抗倾覆弯矩变化对摇摆反应的影响，定义了参数。

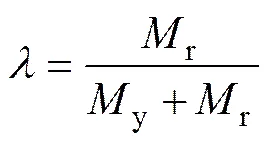
(6)

结合式(4)与式(6)有：

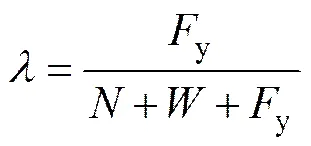
式中：为介于0~1之间；F为限位钢筋的屈服力之和；y为自重提供的抗倾覆弯矩；r为限位钢筋提供的最大抗倾覆弯矩。

由于初始间隙对墩顶的摇摆位移有影响、对墩底弯矩影响很小[11]，取限位钢筋的初始间隙=0。文中(+)=33 873 kN，取=10 m。限位钢筋直径为32 mm，屈服强度为235 MPa，弹性模量=2.1×105MPa，非约束长度=3 m。限位钢筋的取值范围见表6。考虑限位钢筋的初始抗拉刚度r随的变化。提离弹簧刚度及刚臂取值与5.1节中相同。

表6与其对应的关键参数

Table 6and its corresponding key parameters

图14~17和表7所示为El-centro波下的变化对桥墩摇摆反应的影响。

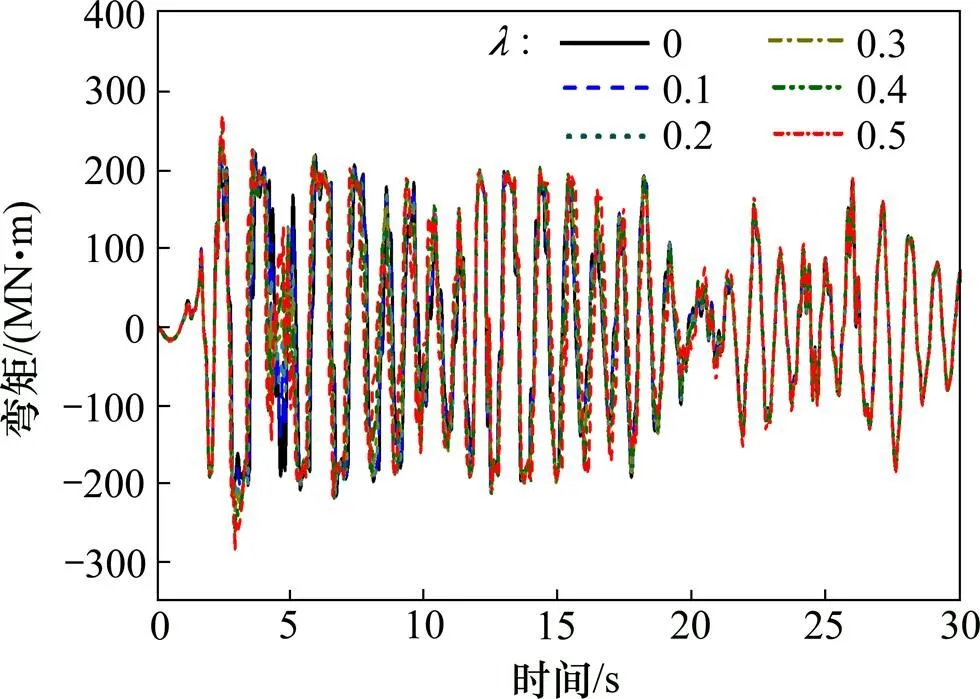
图14 不同λ的墩底弯矩时程曲线比较(El-centro)

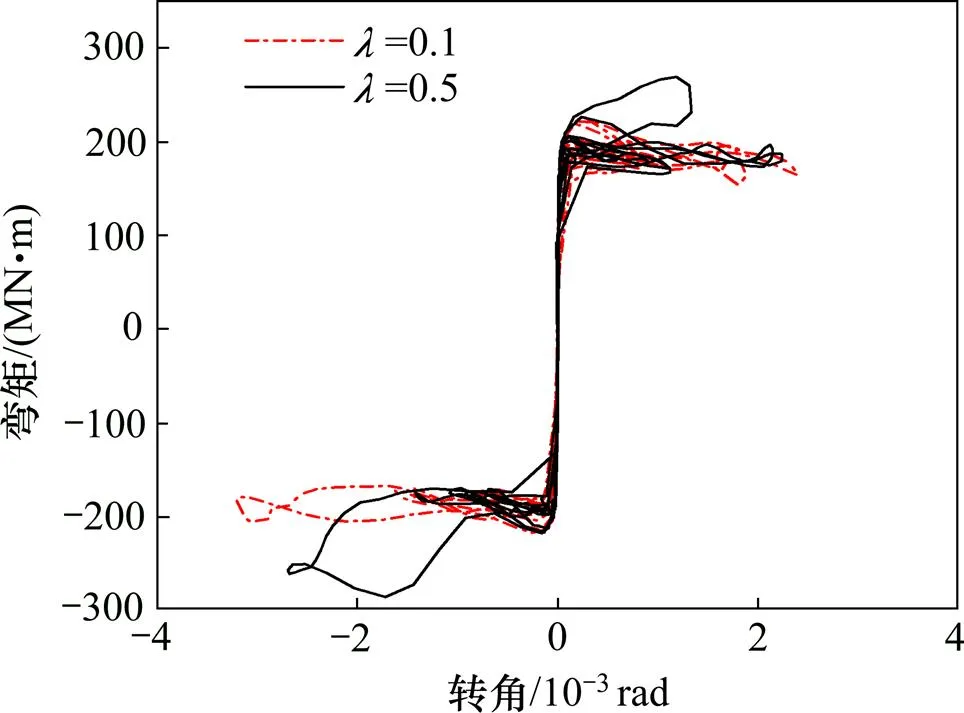
图15 基础底面中心的弯矩与转角的关系(El-centro)

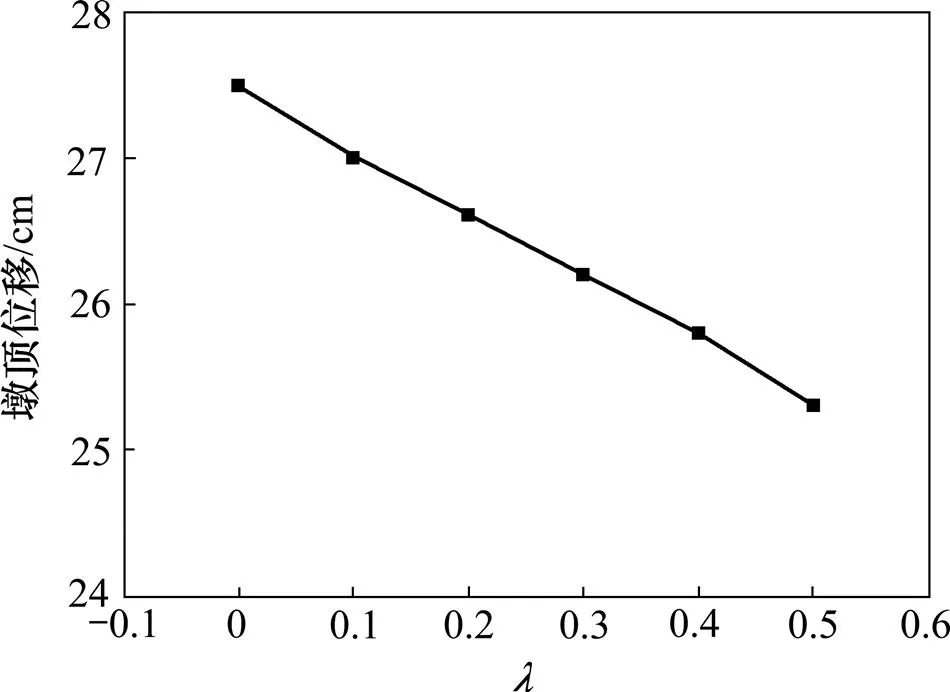
图16 λ与墩顶位移的关系

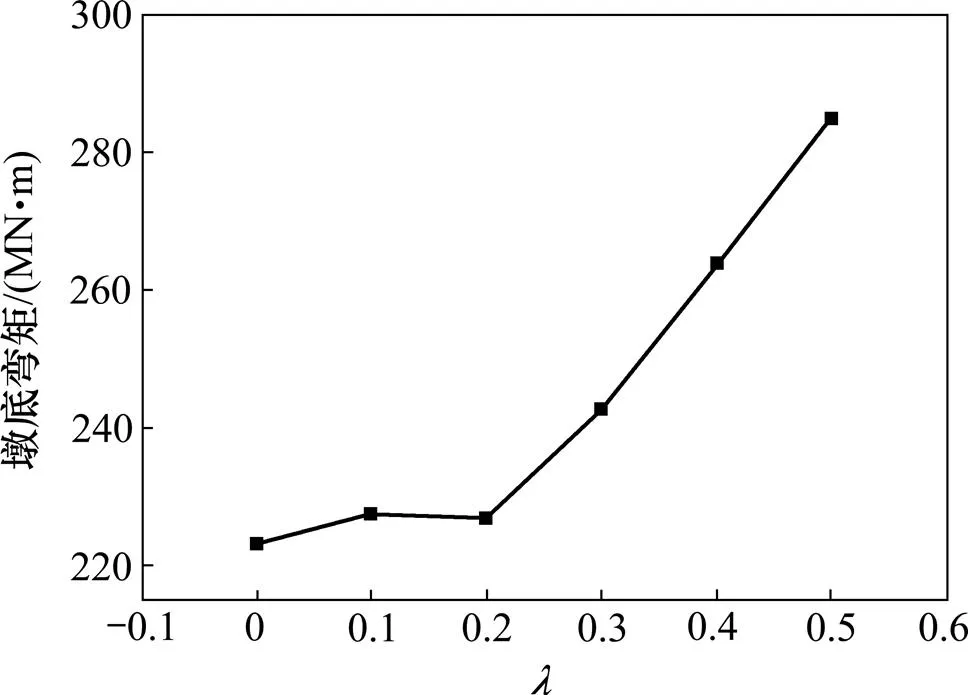
图17 λ与墩底弯矩的关系

表7对摇摆反应的影响(El-centro)

Table 7 Influence ofon rocking response

由图14和表7可以看出：随的增加墩底弯矩时程曲线的形状发生了变化，墩底弯矩及其时程曲线形状有较大影响。由式(5)可知的增加意味着墩底提离弯矩的增大，改变了桥墩的摇摆振动，这是造成墩底弯矩及其时程曲线形状变化的主要原因。

由图15可以看出：=0.1时的基础底面中心的弯矩−转角滞回关系曲线为反“”形，耗回曲线的面积较小、耗能能力极小；而=0.5时的基础底面中心的弯矩−转角滞回关系曲线为“旗帜”形，有一定的耗能能力。这表明，摇摆桥墩的耗能能力随的增大而增大。

由图16和图17及表7可以看出：墩顶位移随的增大而减小，均有明显的线性关系；当为0~0.2时，对墩底弯矩的影响较小，但当为0.2~0.5时墩底弯矩随的增大而增大，其他2条波下也有以上规律。这表明，当小于0.2时，不仅墩顶限位效果较好、而且对墩底弯矩的影响也较小。

5.3 对比分析

基础宽度及参数改变均会引起桥墩的抗倾覆弯矩的变化，桥墩抗倾覆弯矩的变化又会引起其摇摆振动变化，从而影响桥墩的摇摆反应。为了方便比较，以最大抗倾覆弯矩作为指标，将两者相近的抗倾覆弯矩对应的摇摆反应见表8、图18和图19，当=0及=10 m两者具有相同的初始条件。

表8 摇摆反应的对比分析(El-centro)

Table 8 Comparative analysis of rocking response

图18 2种情况的墩顶水平位移时程曲线比较(El-centro)

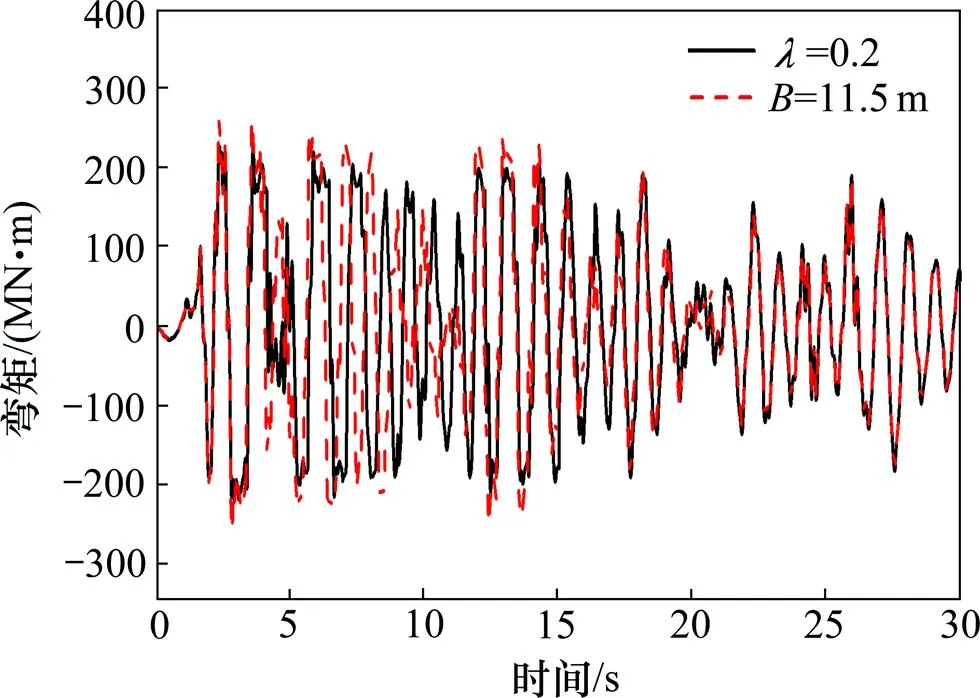
图19 2种情况的墩底弯矩时程曲线比较(El-centro)

由图18和图19可以看出：提离摇摆前(2.5 s之前)及提离摇摆后(15 s之后)两者的时程曲线吻合较好，但在提离摇摆阶段(2.5~15.0 s)之间两者相近的最大抗倾覆弯矩对应的摇摆反应有较大的不同。再结合表8可知：改变对应的墩顶位移及墩底弯矩较初始条件下=0即=10.0 m的变化率明显大于改变。=0.2对应的最大抗倾覆弯矩比初始条件增大20%，=11.5 m对应的抗倾覆弯矩比初始条件增大18.2%，前者比后者的多增加1.8%，但前者墩顶位移反应减小率为3%、远小于后者10.0%。与墩顶位移规律相反，前者墩底弯矩增大率为1.5%、后者墩底弯矩的增大率为17.6%。这是因为，两者作用机理不同所致。限位钢筋提供的抗倾覆弯矩与其中的轴向力有关、随限位钢筋中的轴向拉力在变化(见图20)，其最大值为式(6)中的r。=0.2与=11.5 m两者对应的最大抗倾覆弯矩相差1.8%，即使两者的大抗倾覆弯矩相等，两者发生提离摇摆的条件也不同，前者为墩底地震弯矩大于y=169 365 kN∙m，后者是墩底地震弯矩大于(y+r)= 203 238 kN∙m。同等的最大抗倾覆弯矩下，对应的桥墩比对应桥墩的提离摇摆发生时间的更早、提离次数更多。这是相近最大抗倾覆弯矩下对应的墩顶位移及墩底弯矩较同样初始条件的变化率明显大于变化率的原因。

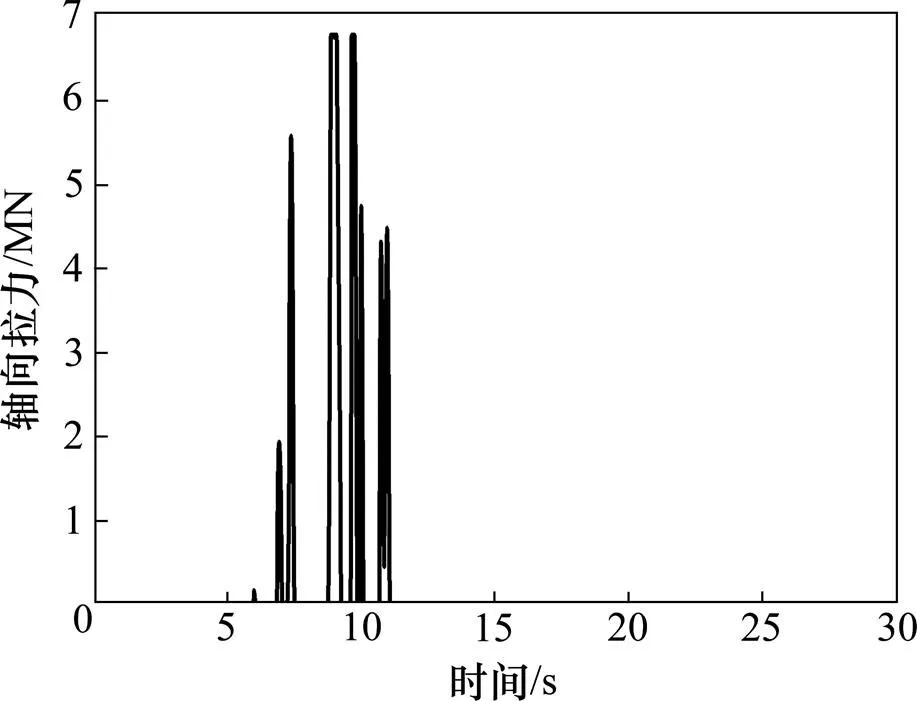
图20 限位钢筋轴向拉力时程曲线(El-centro)

6 结论

1) 基础宽度越小，摇摆振动越剧烈；墩顶位移随基础宽度的增大呈线性减小，墩底弯矩随基础宽度的增大呈近似线性增大。通过改变基础宽度尺寸可控制桥墩的摇摆反应。

2) 提离弹簧刚度越小桥墩的摇摆振动越剧烈、动力放大作用越明显、摇摆反应越大，通过桥墩下方基础材料的调整，也可在一定程度上控制桥墩的摇摆 反应。

3) 墩顶位移随λ增大而线性减小，摇摆桥墩的耗能能力随的增大而增大。墩底弯矩受的影响较复杂，当小于0.2时其对墩底弯矩的影响较小，介于0.2~0.5时墩底弯矩随的增大而增大。

4) 相等的最大抗倾覆弯矩下，调整与改变桥墩的提离摇摆条件不同、得到的摇摆反应也有较大的差异。

5) 为了能有效地控制摇摆反应，桥墩自复位隔震设计时应综合考虑基础宽度、基础材料及。

参考文献：

[1] 夏修身, 陈兴冲, 王常峰. 铁路高墩弹塑性地震反应分析[J]. 世界地震工程, 2008, 24(2): 117−121. XIA Xiushen, CHEN Xingchong, WANG Changfeng. Nonlinear seismic response of the tall RC piers of railway bridges[J]. World Earthquake Engineering, 2008, 24(2): 117−121.

[2] 梁智垚, 李建中. 桥梁高墩合理计算模型探讨[J]. 地震工程与工程振动, 2007, 27(2): 91−98. LIANG Zhiyao, LI Jianzhong.Investigation on rational analyticalmodel of tall bridge pier[J]. Earthquake Engineering and Engineering Vibration, 2007, 27(2): 91−98.

[3] Kunde M C, Jangid R S. Seismic behavior of isolated bridges: A-state-of-the-art review[J]. Electronic Journal of Structural Engineering, 2003(3): 140−170.

[4] Soong T T, Spencer B F. Supplemental energy dissipation: State-of-the-art and state-of-the practice[J]. Engineering Structures, 2002, 24(3): 243−259.

[5] Symans M D, Charney F A, Whittaker A S, et al. Energy dissipation systems for seismic applications: Current practice and recent developments[J]. Journal of Structural Engineering, 2008, 134(1): 3−21.

[6] 夏修身, 陈兴冲, 王希慧.等. 剪力键对隔震桥梁地震反应的影响[J]. 地震工程与工程振动, 2012, 32(6): 104−109. XIA Xiushen, CHEN Xingchong, WANG Xihui, et al. Effect of shear key on seismic response of bridge using isolation bearing[J]. Earthquake Engineering and Engineering Vibration, 2012, 32(6): 104−109.

[7] CALTRANS. Seismic design criteria version 1.4[S].

[8] 夏修身, 陈兴冲. 铁路高墩桥梁基底转动隔震与墩顶减震的效果对比研究[J]. 铁道学报, 2011, 33(9): 102−107. XIA Xiushen, CHEN Xingchong. Controlled rocking and pier top seismic isolation of railway bridge with tall piers[J]. Journal of the China Railway Society, 2011, 33(9): 102−107.

[9] 夏修身. 铁路高墩抗震设计方法研究[D]. 兰州: 兰州交通大学土木工程学院, 2012: 65−68. XIA Xiushen.Research on seismic design of tall piers for railway bridges[D]. Lanzhou: Lanzhou Jiaotong University. School of Civil Engineering, 2012: 65−68.

[10] 夏修身, 陈兴冲.桩基础高墩摇摆隔震分析模型研究[J]. 铁道学报, 2013, 35(11): 86−91. XIA Xiushen, CHEN Xingchong. Study on analytical model of rocking isolation for tall pier with pile foundations[J]. Journal of the China Railway Society, 2013, 35(11): 86−91.

[11] 夏修身, 陈兴冲.限位装置对桩基础高墩摇摆反应的影响[J]. 同济大学学报(自然科学版), 2013, 41(10): 1470−1475. XIA Xiushen, CHEN Xingchong. Effect of the restrainer on the rocking response of tall pier with pile foundations[J]. Journal of Tongji University (Natural Science), 2013, 41(10): 1470−1475.

[12] Gazetas G. Analysis of machine foundation vibrations: State of the art[J]. Soil Dynamics and Earthquake Engineering, 1983, 2(1): 2−41.

[13] PEER. NGA strong motion database[EB/OL]. [2005−03−21]. http://peer.berkeley.edu/NGA

Isolation mechanism of self-centering tall pier

XIA Xiushen1, CHEN Xingchong1, LI Jianzhong2

(1. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. College of Civil Engineering, Tongji University, Shanghai 200092, China)

The isolation mechanism for self-centring tall pier with pile foundations was investigated. Two springs were used to simulate the uplift and rocking of the pier. Rocking response of a railway tall pier was investigated through nonlinear time history analysis by inputting three strong ground motions, considering effects of restrainers on the rocking response. The rocking responses of the pier were discussed such as functions of the stiffness of up-lift spring and width of spreading foot. The results show that the rocking vibration is severe and rocking response of the piers is larger when the stiffness of lift-off spring is smaller. The base moment increases along with. The displacement at pier top decreases whileincreases. It is also observed that displacement at pier top has a linear relation with, but the relation between base moment andis relatively complicated. Rocking response of the tall pier can be controlled by adjusting the width of foundation,and the contact stiffness between the pier and the pile cap.

tall pier; pile foundation; self-centering; isolation mechanism; response control

10.11817/j.issn.1672-7207.2015.07.023

U442

A

1672−7207(2015)07−2549−09

2014−07−09；

2014−10−16

国家自然科学基金资助项目(51368033)；长江学者和创新团队发展计划项目(IRT1139)；国家重点基础研究发展规划(973计划)项目(2013CB036302) (Project(51368033) supported by the National Natural Science Foundation of China; Project(IRT1139) supported by the Program for Changjiang Scholars and Innovative Research Team in University; (Project(2013CB036302) supported by the National Basic Research Development Program of China (973 Program))

夏修身，博士(后)，副教授，从事桥梁抗震及减隔震研究；E-mail: xiaxiushen@mail.lzjtu.cn

(编辑 杨幼平)