高湍流度格栅的数值模拟及设计方法研究
杨荣菲,杨兵,张晓东,葛宁
(1.南京航空航天大学能源与动力学院江苏省航空动力系统重点实验室,南京210016;2.中国燃气涡轮研究院航空发动机高空模拟技术重点实验室,四川江油621703)
高湍流度格栅的数值模拟及设计方法研究
杨荣菲1,杨兵1,张晓东2,葛宁1
(1.南京航空航天大学能源与动力学院江苏省航空动力系统重点实验室,南京210016;2.中国燃气涡轮研究院航空发动机高空模拟技术重点实验室,四川江油621703)
为探讨高湍流度格栅的几何设计方法,采用基于非结构网格的大涡模拟方法,以单平面格栅为研究对象,计算分析了不同格栅稠度、几何形状、来流雷诺数及表面粗糙度下,格栅后湍流度、各向同性特征沿流向的变化。结果表明,格栅稠度对各向同性湍流度基本无影响,稠度增加能增加格栅初始湍流度;存在优化的格栅形状、与格栅尺寸变化相关的来流雷诺数及格栅表面粗糙度,能改善湍流各向同性特征,进而提高格栅湍流度。
高湍流度格栅;单平面格栅;格栅设计;各向同性湍流;大涡模拟;涡轮叶片;热传导
1 引言
航空发动机燃烧室出口的湍流度达15%~20%,有研究表明,主流湍流度增加1%,热传导系数增加5%[1]。实验中,为模拟湍流度变化对叶片表面换热的影响,通常在实验段上游放置主动/被动控制的高湍流度格栅。其中,主动控制高湍流度格栅的控制机构复杂,常用的有射流格栅[2]和三角翼振动格栅[3],最大湍流度能达到20%以上。被动控制格栅结构简单,制造成本低,常用的有单平面及双平面格栅,最大湍流度能达到10%左右,在湍流度相关实验研究[1]中应用范围最广。
湍流理论表明,当格栅后湍流发展至近似均匀各向同性时,湍流强度随距离的增加而指数衰减,即,其中n为负数,M为格栅扰流柱间距。因此,格栅后湍流强度,由初始湍流度、湍流发展至均匀各向同性所需距离、湍流衰减指数共同决定。
国外针对平面格栅湍流开展了大量的实验研究,总结出影响格栅湍流度的主要因素,包括格栅稠度及来流雷诺数。Kurian等[4]和Uberob等[5]的实验研究发现,随着格栅稠度的增加,格栅后初始湍流度增加,衰减指数降低;相同格栅稠度下,随着格栅间距雷诺数的增加,初始湍流度增加,湍流衰减指数增加。国内李静美等[6]研究了4种格栅的湍流度,发现随着来流雷诺数的增大,湍流度增加。故采用一个中等格栅稠度,同时尽量提高来流雷诺数,能提高格栅湍流度。
另外,通过减小湍流发展至均匀各向同性所需距离,也能有效提高格栅湍流度。Comte-bellot等[7]指出,格栅后采用收缩实验段,相比于平直管道,格栅湍流能更快地趋向于各向同性。西工大的低湍流度风洞[8]就采用这种收缩实验段形式。Van Fossen等[9]的实验研究发现,在相同格栅稠度和来流雷诺数下,增加格栅尺寸,能改善格栅湍流的各向同性,进而增加湍流度。此外,采用倾斜格栅[5]或分形格栅[10],也能有效改善格栅湍流的各向同性。故高湍流格栅要求选用合适的格栅几何形状及格栅尺寸。
本文以单平面格栅为研究对象,利用大涡模拟方法,从格栅稠度、几何形状、来流雷诺数及表面粗糙度等方面,研究格栅后湍流的发展,为高湍流度格栅几何设计提供一定的指导。
2 研究对象
单平面格栅的几何示意图见图1,横向、纵向扰流棒的中心线在同一平面上,扰流棒的截面形状可以是圆形、方形、三角形或其他形状。将相邻两扰流棒之间的距离记为M,扰流棒的特征长度记为b,则格栅稠度定义为格栅堵塞面积与总面积的比值,其计算公式见式(1),格栅间距雷诺数的定义见式(2)。式中,U0为来流速度。

由于格栅湍流实验段为正方形对称结构,此时可假设格栅后流动的径向及横向速度脉动水平相同,故可用轴向速度脉动与横向速度脉动的比值来描述均匀各向同性特征,如式(3)所示。
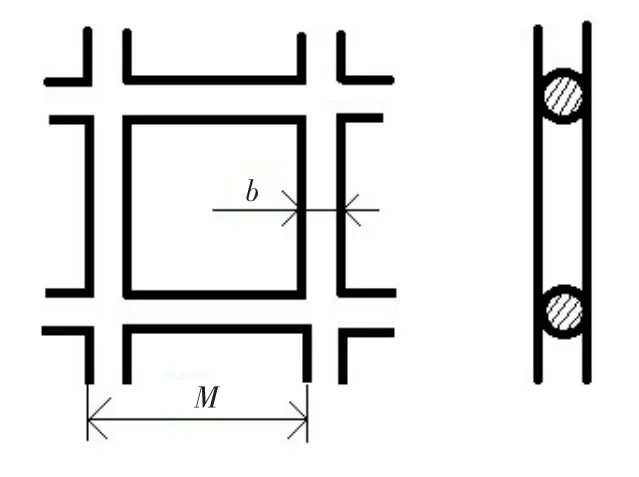
图1 单平面格栅Fig.1 Monoplane grid

式中:HI称为均质度。文献[11]中用HI=1.2作为湍流近似达到均匀各向同性的参考值,本文也采用此参考值。
格栅湍流度的计算式为:
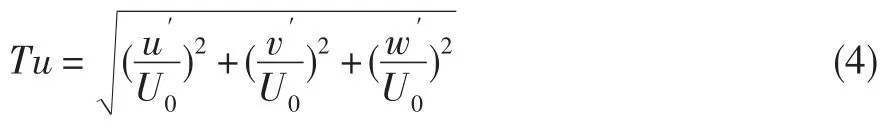
3 数值模拟方法及验证
以文献[11]中单平面圆柱型格栅实验测量结果,对数值模拟方法进行验证,格栅计算域及网格如图2所示。格栅中M=5.0 mm,直径d=1.3 mm,格栅大小为3M×3M,格栅上游计算域长10M,下游计算域长80M。考虑到圆柱交错处结构网格质量难以保证,故在整个计算域内采用非结构网格,并在格栅壁面附近进行加密处理,以保证y+<1。
为得到湍流中不同尺度的涡结构,计算中采用了动态亚格子模型的大涡模拟方法。进口边界处给定速度10 m/s,湍流度1%,出口给定静压101 325 Pa,格栅表面为无滑移边界,计算域上下边界为对称边界,左右边界为周期性边界。文献中实验结果达到最小误差时,PIV采样时间间隔9×10-5s。为加速计算收敛,本文采用非定常计算,时间步长为0.000 2 s。

图2 格栅计算域及网格Fig.2 Grid calculation domain
由于测点位置对湍流度测量值无影响[11],故在过格栅横纵扰流柱交点并平行于管道轴线的直线上布置测点。在0~20M轴向距离内均匀布置20个测点,在20M~40M轴向间距内均匀布置10个测点(图2)。
计算收敛后,取0.06 s内非定常速度脉动结果进行后处理,得到湍流度及均质度沿流向的变化,并与实验结果进行对比,如图3所示。从图中可知:1M处计算得到的初始湍流度与实验值符合较好;在3M~12M距离内,湍流度的计算值与实验值误差较大,最大差值达3%;12M之后,均质度的计算值与实验值均为1.2左右,可认为此时湍流基本达到各向同性。由于本文只对均匀各向同性的格栅湍流感兴趣,故当格栅后湍流达到各向同性时,计算值与实验值间的误差可接受。另一方面,本文主要针对格栅稠度、几何形状、粗糙度等因素对格栅湍流度的影响进行对比研究,计算网格及方法在比较过程中产生的误差可以消除。因此,使用基于非结构网格的大涡模拟方法来获取格栅湍流特性可行,下文的格栅湍流计算采用与图2相同的格栅计算域及网格。
4 格栅湍流的影响因素分析
4.1格栅稠度对湍流衰减的影响
单平面圆柱格栅M=5 mm,d=1.0、1.3、1.5、2.0 mm时,相应的格栅稠度分别为0.36、0.45、0.51、0.64。4种格栅稠度下格栅湍流度及均质度沿流向的变化,如图4、表1所示。可见,随着格栅稠度的增加,格栅的初始湍流度增加,当稠度大于0.45时,初始湍流度达到22%以上。格栅稠度越大,格栅湍流达到各向同性时所需的流向距离越远,但各向同性湍流所对应的湍流度基本相同,即提高格栅稠度并不能获得更高的各向同性湍流度。因此,高湍流度格栅的设计重点,是采用较高稠度格栅的同时,采用有效措施来提高格栅湍流的各向同性特征。

图3 格栅(d=1.3 mm,M=5 mm)湍流计算与实验结果对比Fig.3 Comparison between calculated grid turbulence(d=1.3 mm,M=5 mm)and experimental results
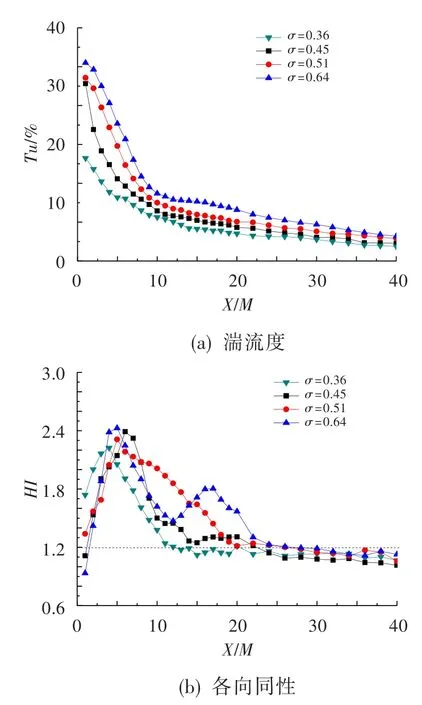
图4 不同稠度格栅湍流衰减情况Fig.4 Grid turbulence decay at different grid solidity
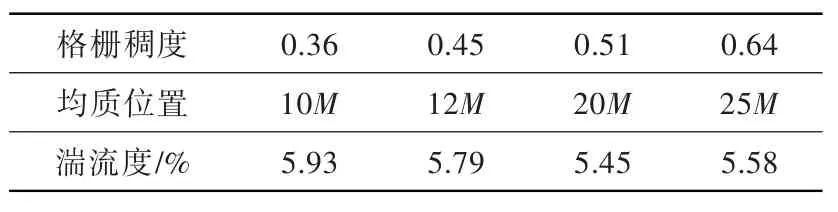
表1 不同稠度格栅湍流各向同性特征的初始流向位置Table 1 The stream-wise initial isotropic position of grid turbulence at different grid solidity
4.2格栅几何形状对湍流衰减的影响
为获取高湍流度水平的各向同性流动,下文的研究都针对稠度为0.64的格栅开展,以得到高的初始湍流强度;格栅计算面积增大为5M×5M,以减少计算格栅与实验格栅的几何差异。
如图5所示,设计4种扰流柱形状的格栅:方形格栅、反三角形格栅、三角形格栅及菱形格栅。格栅扰流柱截面积均与圆柱形格栅的相同,流体从左向右流动。计算得到4种格栅后湍流度及均质度沿流向的发展,并与圆柱形格栅湍流特性进行对比,如图6所示。可见,三角形格栅产生的湍流度最小,各向同性特征最差;倒三角形格栅虽能提高格栅的初始湍流度,但其各向同性初始位置相比圆形格栅离格栅更远,即其所对应的格栅湍流水平更低,不利于高湍流度格栅湍流的生成;方形格栅产生的初始湍流度高于圆柱形格栅,且达到各向同性的初始位置与圆柱形格栅相同,导致其各向同性湍流度高于圆形格栅;菱形格栅的湍流度衰减情况与圆形格栅相同,但其各向同性特征得到明显改善。不同几何形状格栅湍流达到各向同性时所对应的流向位置及湍流度对比见表2。可见,相较于方形格栅通过提高初始湍流度来提高湍流度,菱形格栅通过减小流动发展至各向同性湍流的距离,获得的湍流度提升更明显。而由图8中可知,当来流速度和稠度不变时,格栅扰流柱间距引起的雷诺数变化对格栅湍流度的衰减基本无影响,但格栅尺寸变化改变了各向同性湍流所对应的初始位置,且存在一个最佳格栅扰流柱间距,使格栅湍流各向同性初始位置离格栅最近,即相应的湍流度水平最高,见表3。因此,高雷诺数下,雷诺数对格栅湍流的影响主要与格栅尺寸相关,故可通过减小湍流发展至各向同性的距离来提高湍流度。此结论与文献[5]中大尺寸格栅有利于改善格栅湍流各向同性的结论相一致。

图5 4种不同几何形状格栅示意图Fig.5 Four different grid geometries
4.3雷诺数对湍流衰减的影响
由式(2)可知,可通过增加来流速度或格栅扰流柱间距来提高格栅间距雷诺数。以单平面圆柱格栅为研究对象,分别改变来流速度和格栅扰流柱间距,计算得到格栅湍流度及均质度沿流向的发展,结果分别如图7、图8所示。由图7中可知,当格栅尺寸及稠度不变时,来流速度改变引起的格栅雷诺数变化,对格栅湍流度衰减及各向同性衰减基本无影响。
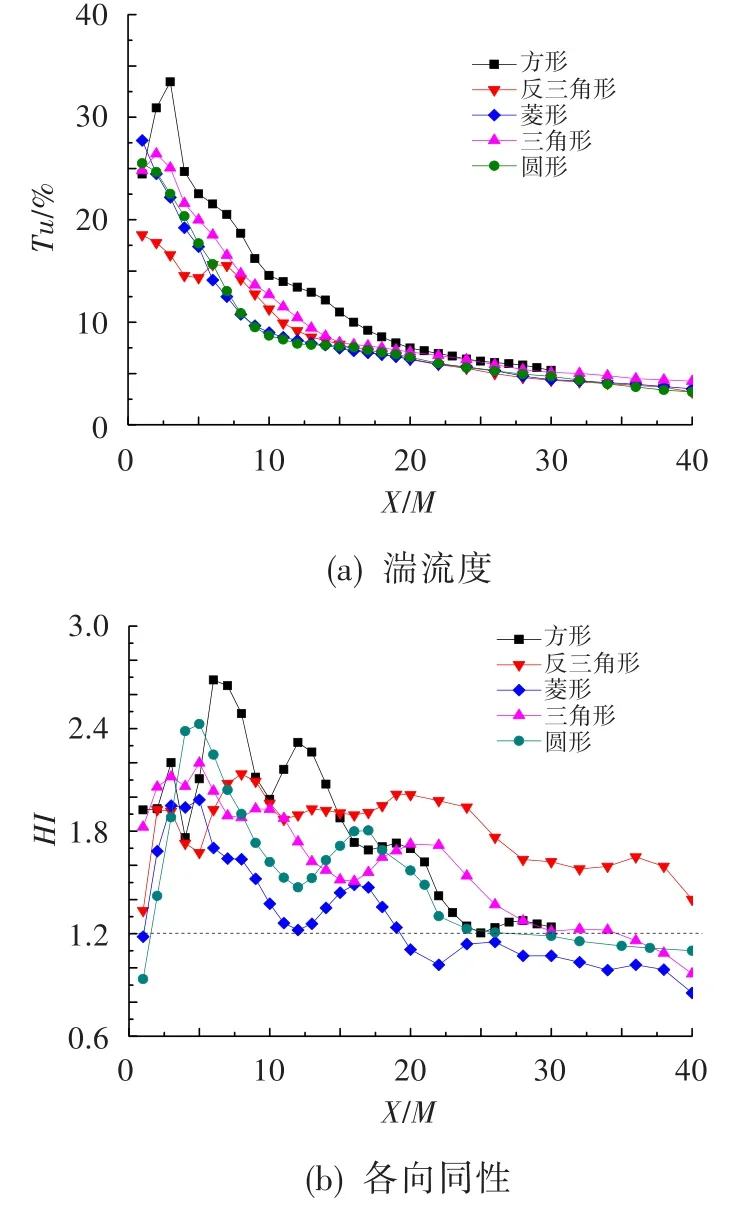
图6 不同几何形状格栅湍流衰减情况Fig.6 Grid turbulence decay for different grid geometry
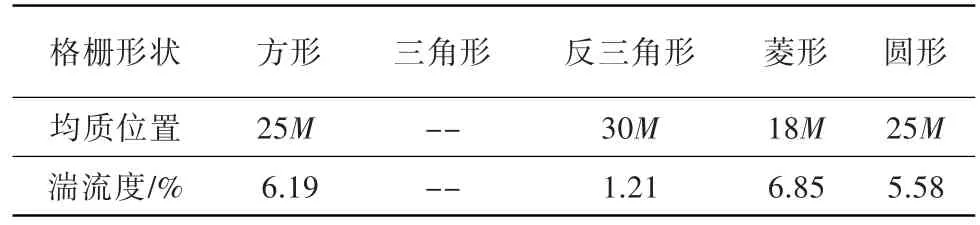
表2 不同几何格栅湍流各向同性特征的初始流向位置Table 2 The stream-wise initial isotropic position of grid turbulence for different grid geometry
4.4表面粗糙度对湍流衰减及均质度的影响
格栅材料不同,其表面粗糙度也不同。以不锈钢的表面粗糙度20 μm作为参考,设置表面粗糙度水平分别为20 μm、50 μm及80 μm,以单平面方形格栅为研究对象,计算不同粗糙度下格栅湍流度及均质度沿流向的变化,结果如图9所示。可见,粗糙度的改变对湍流度衰减基本无影响,主要影响格栅湍流均质度的变化。当格栅粗糙度从20 μm增至50 μm时,格栅各向同性特征得到一定程度改善,特别是临近格栅的流动距离内,格栅湍流的各向同性特征改善最明显;当粗糙度进一步增加时,格栅的各向同性特征不再变化,见表4。因此,存在一个最佳粗糙度,能小幅改善格栅湍流的各向同性特征,进而获得高湍流度格栅。
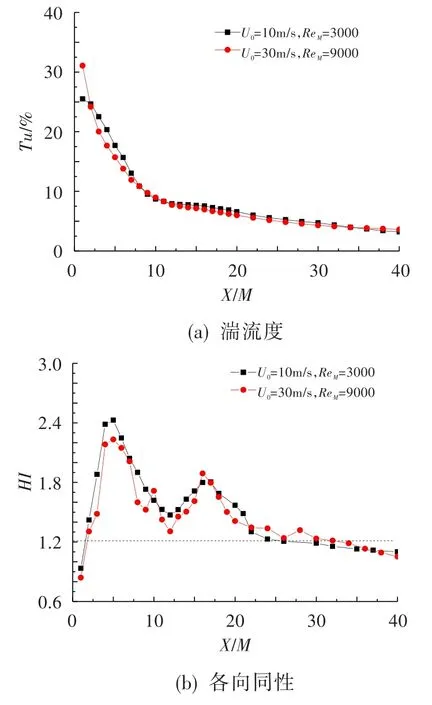
图7 来流速度相关雷诺数变化对格栅湍流衰减的影响Fig.7 Grid turbulence decay at different Reynolds number varied with inflow velocity

图8 格栅扰流柱间距相关雷诺数变化对格栅湍流衰减的影响Fig.8 Grid turbulence decay at different Reynolds number varied with grid spacingM
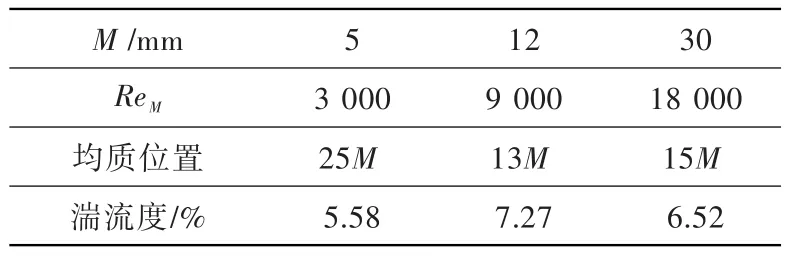
表3 不同格栅扰流柱间距格栅湍流各向同性特征的初始流向位置Table 3 The stream-wise initial isotropic position of grid turbulence at different grid spacingM
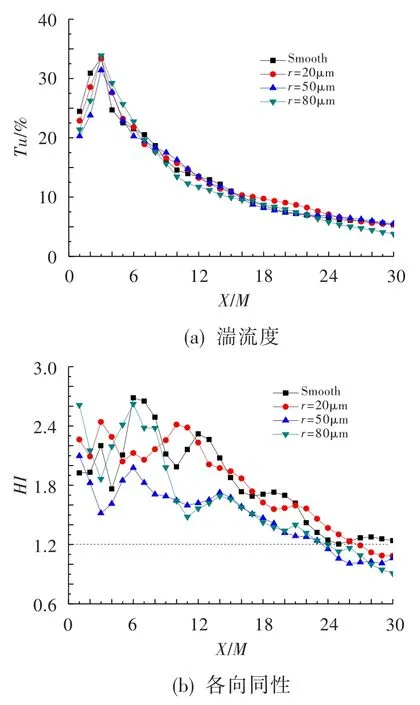
图9 粗糙度对格栅湍流衰减特性的影响Fig.9 Grid turbulence decay with different surface roughness
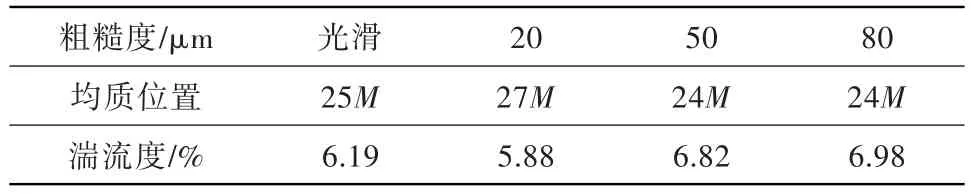
表4 不同粗糙度格栅湍流各向同性特征的初始流向位置Table 4 The stream-wise initial isotropic position of grid turbulence with different grid surface roughness
5 结论
本文以单平面格栅为研究对象,使用基于非结构网格的大涡模拟方法,数值研究了格栅稠度、几何形状、来流雷诺数及格栅表面粗糙度对格栅湍流的影响,得到如下结论:
(1)随着格栅稠度的增加,格栅的初始湍流度增加,但格栅湍流达到各向同性时所对应的湍流度基本不变。
(2)格栅几何形状对格栅湍流度的影响较大,并显著影响湍流各向同性特征沿流向的发展;其中菱形格栅后各向同性湍流的湍流度最大。
(3)来流速度引起的雷诺数变化对格栅后湍流基本无影响,而格栅尺寸引起的雷诺数增大会显著改善格栅湍流各向同性特征。
(4)格栅表面粗糙度对湍流度基本无影响,但存在一个最佳的格栅表面粗糙度,小幅改善格栅湍流各向同性特征。
[1]Mehendale A B,Han J C,Ou S.Influence of high mainstream turbulence on leading edge heat transfer[J].ASME Journal of Heat Transfer,1991,113:843—850.
[2]Gad-el-hak M,Corrsin S.Measurements of the nearly isotropic turbulence behind a uniform jet grid[J].Journal of Fluid Mechanics,1974,62:115—143.
[3]Poorte R E G,Biesheuvel A.Experiments on the motion of gas bubbles in turbulence generated by an active grid[J]. Journal of Fluid Mechanics,2002,461:127—154.
[4]Kurian T,Fransson J H M.Grid-generated turbulence revisited[J].Fluid Dynamics Research,2009,41(2):1—32.
[5]Uberob M S.Effect of grid geometry on turbulence decay[J].The Physics of Fluids,1967,10(6):1216—1224.
[6]李静美,赵润民,翟曼玲.格栅下游湍流特性的研究[J].空气动力学报,1993,11(4):440—444.
[7]Comte-bellot G,Corrsin S.The use of a contraction to improve the isotropy of grid-generated turbulence[J].Journal of Fluid Mechanics,1966,25(4):657—682.
[8]白存儒,何克敏,郭渠渝,等.西工大低湍流度风洞的变湍流度技术[J].气动实验与测量控制,1995,9(4):14—19.
[9]Van Fossen G J,Ching C Y.Measurements of the influence of integral length scale on stagnation region heat transfer[R].NASA TM-106503,1994.
[10]Seoud R E,Vassilicos J C.Dissipation and decay of fractal-generated turbulence[J].Physics of Fluids,2007,19:105108-1—11.
[11]Avallone G,De Gregorio F,Romano G P.PIV measurements of turbulence decay behind a grid[C]//.Particle image velocimetry:recent improvements.Springer Berlin Heidelberg,2004:263—277.
Study on numerical simulation and design method of high turbulence grid
YANG Rong-fei1,YANG Bing1,ZHANG Xiao-dong2,GE Ning1
(1.Jiangsu Province Key Laboratory of Aerospace Power Systems,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.Key Laboratory on Aero-Engine Altitude Simulation Technology,China Gas Turbine Establishment,Jiangyou 621703,China)
In order to explore the design method of monoplane grid,the turbulence intensity and isotropy behind the grid with different solidity,geometry,Reynolds number and surface roughness were investigated by using large eddy simulation technology.The results show that the isotropic turbulence does not change with increased grid solidity which increases the grid initial turbulence level.And the grid turbulence intensity can be raised by adopting an appropriate geometry,Reynolds number and surface roughness to improve the grid turbulence isotropy.
high turbulence grid;monoplane grid;grid design;isotropic turbulence;large eddy simulation;turbine blade;heat transfer
V211
A
1672-2620(2015)04-0001-06
2014-10-24;
2015-08-18
中国航空科学基金(2012ZB24009)
杨荣菲(1982-),女,湖北武汉人,讲师,博士,主要从事叶轮机械气动热力学研究。

