Exponent及Gauss型遥测数据建模初始化算法

王永生，杜彬彬，孙　瑾，杨海峰

（1.海军航空工程学院a.兵器科学与技术系；b.指挥系，山东烟台264001；2.中国航天科技集团513所，山东烟台264003）

Exponent及Gauss型遥测数据建模初始化算法

王永生1a，杜彬彬1b，孙瑾1a，杨海峰2

（1.海军航空工程学院a.兵器科学与技术系；b.指挥系，山东烟台264001；2.中国航天科技集团513所，山东烟台264003）

在对某大型航天电子设备的遥测数据建模时，经常遇到含有指数类变化规律的数据，对其进行建模可以为研究设备性能的变化规律、实际与设计的差异等提供手段。针对有指数变化趋势的遥测数据，采用Exponent模型、Gauss模型对遥测数据建模，给出了这种数据模型的表达式，研究了2种模型的参数初始化算法。通过数值实验说明模型参数初始化算法的有效性，为后续利用最优化理论求解模型精确参数提供了良好的初试点。

遥测数据；指数模型；Gauss模型；初始参数

利用大型航天电子设备的历史采集数据，采用适当的数学模型，开发对电子设备遥测数据变化进行分析的工具，实现对航天电子设备采集数据进行建模，可以为研究大型电子设备性能的变化规律、分析实际变化与设计值的差异等提供手段。对于大量表现出指数类型变化的遥测数据，须要给出可行的数据模型。模型要求具有一定适用性，不局限于某一个特定的遥测数据。另外，从工程应用的实际需要考虑，还必须根据遥测的数据能够快速计算出模型的初始参数，也就是要有模型参数的初始化算法［1］。求出的初始参数，未必是模型参数的精确解，但可为后续利用最优化理论的方法迭代求解更为精确的解模型参数提供较好的初始点，极大地提高迭代收敛速度［2-6］，满足工程应用需要。

指数型数据［7-9］和Gauss型数据［10-11］是在工程中广泛遇到的信号类型。本文结合遥测数据分析这2种类型遥测数据建模问题，着重探讨模型参数初始化算法。为了工程应用需要采用的数据处理方法必须满足时间复杂度需要，即要求尽可能短的时间完成建模，由于这2种模型的基础都是指数函数exp（t），可以看作是在指数基础上的t的一阶函数和二阶函数，而且Gauss型数据一般具有峰值，充分利用这些特点，并借助最小二乘算法利用大量数据来拟合得到好的模型参数初始值，相对于文献［8-9］中同伦交替迭代法和差分进化算法等而言，不需要复杂的运算，计算速度快，而且获得的模型初始点比较理想，后续就可利用最优化方法中的Levenberg-Marquardt算法［12-14］或者Trust-Region算法［15-16］通过较少次数的迭代计算求得精确模型参数。

为了方便计算，通常要先对数据进行预处理，剔除野值，对采样数据进行去均值并进行必要的尺度压缩，即将数据大小幅值和坐标宽度变换到一定数值范围内，文中假设已完成上述预处理过程。将要处理的遥测数据序列转换为（y，t），其中y和t均为m维列向量，m即为所获得的原始遥测数据的个数。

1　Exponent模型

1.1模型表达式

Exponent模型能够较好地建模拟合具有指数变化趋势的数据，具有比多阶多项式模型更简洁的表达形式，但是考虑到指数迅速上升的情况，本文仅考虑1～2阶指数模型。这里给出其2阶Exponent模型，该模型如下：

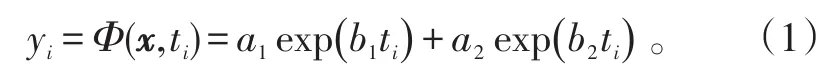
1.2参数初始化算法

模型的初始参数对后续模型求解影响极大，初始参数如选取不当，一方面可能得不到好的最终模型参数，另一方面可能造成循环迭代搜索次数过多，计算时间过长，不具备实用性。求取Exponent指数模型时，注意除剔除野值外不要进行纵横坐标压缩及去均值操作，尽可能保持数据的指数变化趋势不改。

注意到Exponent模型的指数特点，通过合理的数据分段化并计算累加和，利用对数比来确定关键的指数项上ti的系数，并求线性系数。下面分别给出1阶和2阶指数模型的参数初始化算法。

算法1：求1阶Exponent模型初始参数。

2）计算横坐标 t的差分序列，并取均值，即tav=mean（diff（t））。

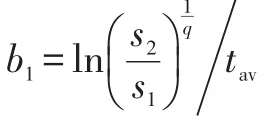
4）最后用最小二乘求取另外一个系数a1：

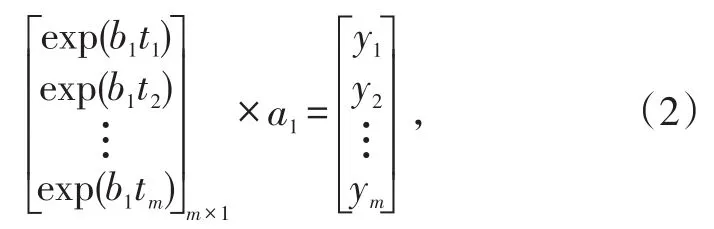
记为B×a1=Y，即

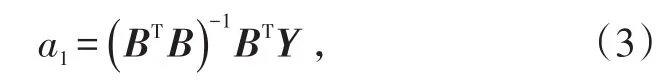
或者直接估计

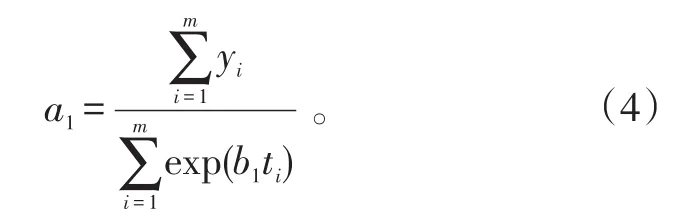
注意，在算法1中要适当调整选取的数据段，避免出现s1=0。

算法2：求2阶Exponent模型初始参数。

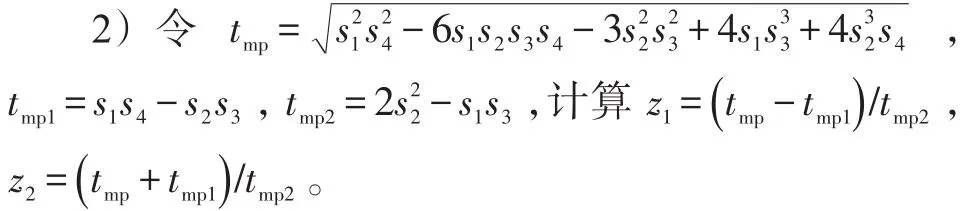
3）计算横坐标 t的差分序列，并取均值，即tav=mean（diff（t））。

5）最后，用最小二乘求取另外2个系数（a1，a2）：

2　Gauss模型

2.1模型表达式

对于一些呈现拱形特点的遥测数据，还可以采用Gauss模型进行拟合总体趋势，但要注意Gauss模型不适合做长期预测。这里给出3阶Gauss模型，该模型表达式如下：

2.2参数初始化算法

考虑到Gauss模型可以看作是指数函数exp（t）基础上的t的2阶函数，并且Gauss模型数据具有峰值的优点，通过拟合方法先求含最大峰值的模型阶中t的2阶函数参数bi、ci，再从原数据消除该阶Gauss模型，逐步求取余下各阶Gauss模型参数。

以3阶Gauss模型为例，说明模型参数初始点x0（即初始参数）的求取过程：依次寻找3次数据序列的最大值，每次找到最大值的索引并记录其值（作为ai）和横坐标（作为bi）；寻找数据中大于0和小于最大值的所有数据，根据Gauss数据特点，求出一个拟合的ci；然后消除数据中的该阶Gauss函数影响，继续求其他阶Gauss函数参数；如果在求某一阶模型参数时不存在大于0和小于最大值的特例时，则由横坐标插值得到bi，ai仍取余下数据序列的最大值，而ci取前面2阶参数b的差值。具体算法如下。

算法3：求Gauss模型初始参数。

步骤1：循环3次求取3个Gauss函数参数。

1）找到数据中的最大值的索引k，令a等于最大数据值，即a=yk，b等于最大值对应的坐标，即b=tk。

2）寻找所有大于0且小于a的数据值；如果没有满足条件的数据则退出，不再寻找其他阶Gauss函数参数。

3）根据上次寻到的数据索引，估算该阶Gauss函数的c值，即

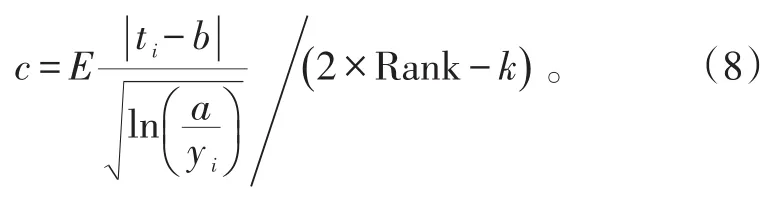
式（8）中：分子部分是对寻找的满足要求的数据计算均值，分母部分中的Rank是采用的模型阶数，本例即为3；k是已经找到初始参数的Gauss函数个数。

从数据序列中除去该阶Gauss函数数据。

步骤2：如果步骤1中2）出现找不到满足条件的数据，则采用如下措施。

1）先找到还差几阶Gauss函数参数没有找到。

2）根据最小和最大横坐标进行差值排序（说明：主要用在数据没有按照横坐标大小顺序排列的情况）。

3）待求的其余阶Gauss函数参数的b即取前面排列的最后几个数据。

4）待求的其余阶Gauss函数参数的a均取余下数据序列y的最大值。

5）待求的其余阶Gauss函数参数的a均取2）排序后的第2个数减第1个数的值。

3　数值实验

3.1Exponent模型实验

考虑 1阶 指 数函数 y=0.05exp（0.000 5t），t=1，2，…，2 000，用算法1求出模型参数初始点后拟合结果如图1 a）所示；再考虑2阶指数函数y=0.05exp（0.000 5t）+0.3exp（0.006t），t=1，2，…，2 000，用算法2求出模型参数初始点后拟合结果如图1 b）所示。

事实上，分别用算法1和算法2求出的上述模型参数初始点与真实参数几乎相同。

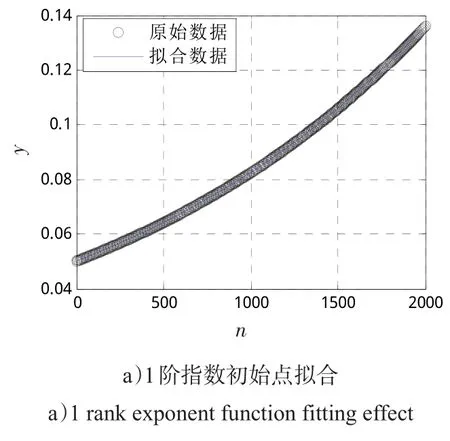
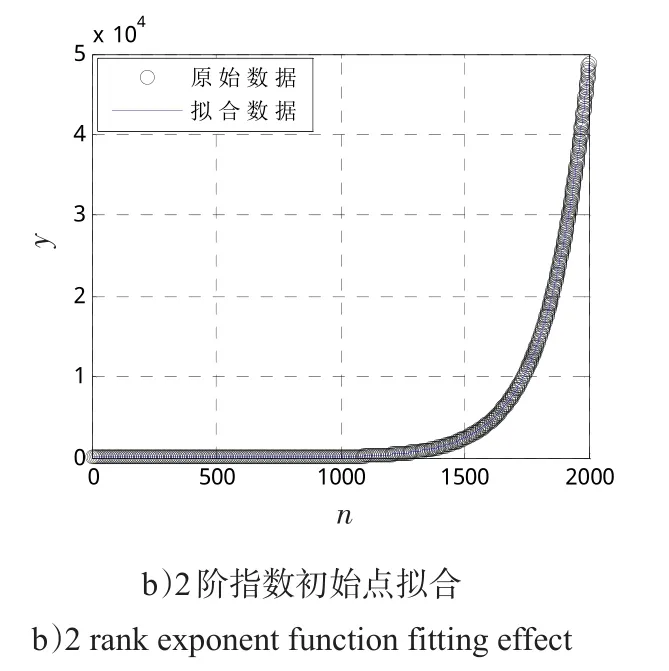
图1　典型指数模型初始点拟合效果Fig.1 Fittingeffectusing classical exponent model initial parameters

对如图2中所示某遥测的均匀缓变类型数据，剔除粗大误差后，考虑分别用1阶指数模型和2阶指数模型和算法求取模型参数初始点，在初始点处的拟合结果分别如图2 a）和b）所示。

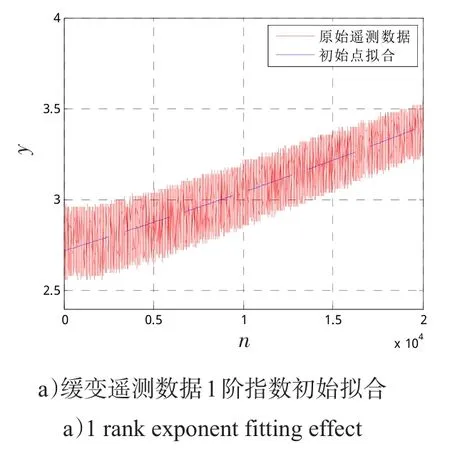
图2　均匀缓变遥测数据初始点拟合数据Fig.2 Slow-changing style fittingeffect using exponent model initial parameters

3.2Gauss模型实验

考虑3阶Gauss模型

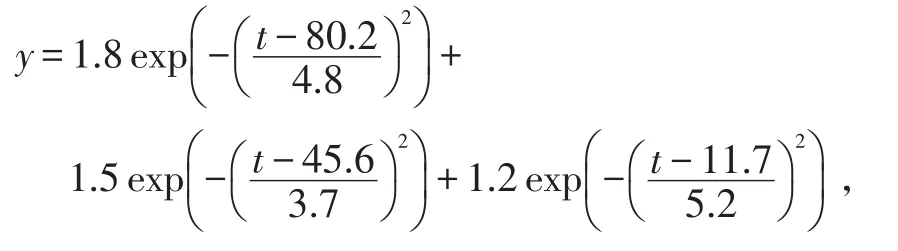
t=1，1.01，1.02，…，100，原始数据和采用算法3求出模型参数初始点拟合后的数据如图3所示。事实上，分别用算法3求出的3阶Gauss模型参数初始点为（1.800 0，80.200 0，4.120 3，1.500 0，45.600 0，3.189 1，1.200 0，11.700 0，4.922 8）与真实参数十分逼近。

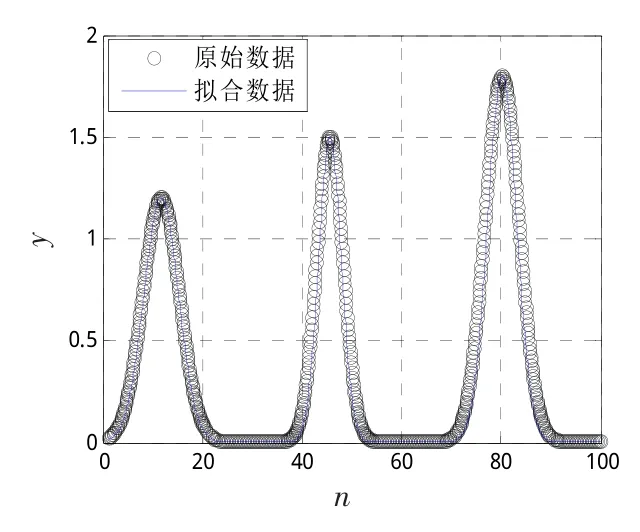
图3　3阶Gauss模型初始点拟合效果Fig.3 Fittingeffectusing three rank Gauss model initial parameters

对图4中所示某遥测的拱形数据，考虑用3阶Gauss模型对其建模拟合，求取模型初始参数。图4 a）图给出了用算法3中前2个步骤求取初始点后拟合结果图；用步骤3采用最小二乘求取系数后，在初始点处拟合结果如图4 b）所示。可以看出，最后用最小二乘有效地解决处理了一段奇异数据的影响。

图4　拱形遥测数据Gauss模型初始点拟合效果Fig.4 Vaulted style fitting result using Gauss model initial parameters

有了上述模型初始点，后续再采用最优化方法中的Levenberg-Marquardt算法或Trust-Region算法迭代几次就能求出较为精确的3阶Gauss模型参数，满足实时性建模要求，最终建模结果如图5所示。

图5　拱形遥测数据Gauss模型建模结果Fig.5 Gauss modeling result of arched telemetry data

4　结束语

对于指数类型的遥测数据，给出能够较好实现对这种数据建模的Exponent模型和Gauss模型，根据数据规律研究了2种模型的参数初始化算法，并对遥测数据进行了数值实验，实验结果说明模型初始化算法可以提供了良好的初始点，计算复杂度低，有利于进一步采用优化算法快速求得全局最优点，获得更为精确的模型参数，实现对某大型航天电子设备遥测数据的准确建模。

［1］李奎山.超越方程的诺模图求解［J］.石油大学学报：自然科学版，1996，20（2）：118-119. LI KUISHAN.Nomography solution of the transcend equation［J］.Journal of the University of Petroleum：Nature Science，1996，20（2）：118-119.（in Chinese）

［2］PHILIP E GILL，WALTER MURRAY，MARGARET H WRIGHT.Practical optimization［M］.London：Academic Press，1981：83-153.

［3］刘兴高，胡云卿.应用最优化方法及Matlab实现［M］.北京：科学出版社，2014：89-109. LIU XINGGAO，HU YUNQING.Optimal methods application and its Matlab implementation［M］.Beijing：Science Press，2014：89-109.（in Chinese）

［4］倪勤.最优化方法与程序设计［M］.北京：科学出版社，2009：25-39. NI QIN.The optimal methods and its Matlab programmer design［M］.Beijing：Science Press，2009：25-39.（in Chinese）

［5］马昌凤.最优化方法及其Matlab程序设计［M］.北京：科学出版社，2010：87-98. MA CHANGFENG.The optimal methods and its Matlab programmer design［M］.Beijing：Science Press，2010：87-98.（in Chinese）

［6］袁亚湘，孙文瑜.最优化理论与方法［M］.北京：科学出版社，1997：373-399. YUAN YAXIANG，SUN WENYU.The Optimation theory and methods［M］.Beijing：Science Press，1997：373-399.（in Chinese）

［7］韩丹，江春，付鹏涛，等.探测器信号波形离散序列的多项式与双指数曲线拟合及其在数字化核能谱中的应用［J］.核电子学与探测技术，2010，30（8）：1075-1078. HAN DAN，JIANG CHUN，FU PENGTAO，et al.Polynomial and Bi-exponential curve fitting for discrete time sequences of detector signals and its application in digitized nuclear spectrum［J］.Nuclear Electronics&Detection Technology，2010，30（8）：1075-1078.（in Chinese）

［8］陈华，邓少贵，范宜仁.同伦交替迭代法在双指数拟合中的应用［J］.计算机工程与应用，2007，43（25）：204-205，226. CHEN HUA，DENG SHAOGUI，FAN YIREN.Application of homotopy alternative iteration method in double exponential fitting［J］.Computer Engineering andApplications，2007，43（25）：204-205，226.（in Chinese）

［9］陈华，邓少贵，李智强，等.差分进化算法在双指数拟合中的应用［J］.计算机工程与应用，2008，44（16）：231-232，235. CHEN HUA，DENG SHAOGUI，LI ZHIQIANG，et al. Application of differential evolutional algorithm in double exponential fitting［J］.Computer Engineering and Applications，2008，44（16）：231-232，235.（in Chinese）

［10］陈维真，张春华，赵仕伟，等.卫星遥感海面高度图像的中尺度涡自动提取［J］.光学精密工程，2013，21（10）：2704-2712. CHEN WEIZHEN，ZHANG CHUNHUA，ZHAO SHIWEI，et al.Automatic detection of mesoscale eddy for satellite remote sea surface height image［J］.Optics and Precision Engineering，2013，21（10）：2704-2712.（in Chinese）

［11］韩艳丽，刘峰，张健，等.天文观测星图中亮线的去除方法［J］.光电工程，2013，40（8）：47-51，58. HAN YANLI，LIU FENG，ZHANG JIAN，et al.Bright line removal algorithm of star-sky image in astronomic observation［J］.Opto-Electronic Engineering，2013，40（8）：47-51，58.（in Chinese）

［12］周小林，孙东松，钟志庆，等.Levenberg-Marquardt算法在测风激光雷达中的应用［J］.红外与激光工程，2007，36（4）：500-504. ZHOU XIAOLIN，SUN DONGSONG，ZHONG ZHIQING，et al.Application of Levenberg-Marquardt algorithm in the wind lidar［J］.Infrared and Laser Engineering，2007，36（4）：500-504.（in Chinese）

［13］李合平，邹明虎，王志云，等.基于L-M算法的雷达板级电路快速故障诊断［J］.测试技术学报，2004，28（4）：364-368. LI HEPING，ZOU MINGHU，WANG ZHIYUN，et al. Board-grade circuit fault quick diagnosis in radar based on L-M algorithm［J］.Journal of Test and Measurement Technology，2004，28（4）：364-368.（in Chinese）

［14］ZHANG RUIJIE，LI LEI，CHEN ZHONGWEI，et al.Calculation of phase equilibria based on the levenberg-marquardt method［J］.Journal of Material Science Technolo-gy，2005，21（1）：10-12.

［15］吴晓丽，倪勤，刘浩.新锥模型二维子空间信赖域算法［J］.高等学校计算数学学报，2012，34（4）：316-327. WU XIAOLI，NI QIN，LIU HAO.Trust-region algorithm using two-dimensional subspace technique with new conic model［J］.Numerical Mathematics a Journal of Chinese Universities，2012，34（4）：316-327.（in Chinese）

［16］XU HUINING，SUN LINPING.An iterated-subspace minimization methods with symmetric rank-one updating［J］.Numerical Mathematics a Journal of Chinese Universities：English Series，2004，13（2）：233-240.

Telemetric Data Modeling and Its Parameters Initial Algorithm of Exponent and Gauss Model

WANG Yongsheng1a，DU Binbin1b，SUN Jin1a，YANG Haifeng2
（1.Naval Aeronautical and Astronautical University a.Department of Ordnance Science and Technology；b.Department of Command，Yantai Shandong 264001，China；2.No.513 Institute of China Aerospace and Technology Corporation，Yantai Shandong 264003，China）

The telemety data of the large-scale spaceflight electronic equipment usually appears the similarly exponent style change.The performance abnormity and the different between the practice and the designed would be discovered ear⁃ly through modeling on these data.In order to modeling the exponent style telemety data，the two models of Exponent and Gauss were introduced.The formula of the two mathematic models were put forward.Then the initial algorithms for the pa⁃rameters of these models were researched.Lastly the numerical experiments results showed the validity of these initial pa⁃rameters algorithms，which afforded the favorable initial starts points for the subsequent optimization theory to compute the accurate model parameters.

telemety data；exponent model；Gauss model；initial parameters

TP399

A

1673-1522（2015）06-0547-06DOI：10.7682/j.issn.1673-1522.2015.06.010

2015-08-23；

2015-10-08

王永生（1978-），男，副教授，博士。