杂波环境下基于数据压缩的多传感器容积滤波算法

刘　俊，刘　瑜，董　凯，孙　顺

（海军航空工程学院a.研究生管理大队；b.信息融合研究所，山东烟台264001）

杂波环境下基于数据压缩的多传感器容积滤波算法

刘俊a，刘瑜b，董凯b，孙顺a

（海军航空工程学院a.研究生管理大队；b.信息融合研究所，山东烟台264001）

针对杂波环境下非线性系统中多传感器多目标跟踪问题，基于广义多维分配（S-D分配）规则获取最佳的量测划分，通过多传感器数据压缩技术得到等效量测点与等效量测协方差，结合容积卡尔曼滤波原理实现多目标跟踪，提出了一种基于数据压缩的多传感器容积滤波算法（SD-DCCKF）。仿真结果表明：相对已有算法，SDDCCKF不仅避免了因模型线性化误差导致的滤波发散问题，而且克服了算法在高维系统中数值不稳定的缺点，算法估计精度较高，收敛速度较快，能够更加有效地解决非线性系统中的多目标跟踪问题。

多维分配；数据压缩；多传感器；多目标跟踪；数据关联；容积卡尔曼滤波

多传感器信息融合系统利用多个传感器对同一目标的观测信息按照一定的规则进行有效地融合处理，能够避免单传感器目标跟踪的一些缺点与局限性，获取更加完整的战场态势信息，为战场指挥决策提供更加准确可靠的依据［1-6］。另一方面，随着计算机技术、通信技术和微电子技术的发展，各种面向非线性复杂应用背景的多传感器系统也越来越受到重视并逐步得以应用，杂波环境下非线性系统多目标状态估计已受到国内外学者的广泛关注［2，7-8］。

多目标跟踪问题的关键在于点航互联，针对这一问题，学者开展了大量的研究，并提出了许多卓有成效的关联算法。其中，概率数据互联算法（Probabilistic Data Association Algorithm，PDA）能较好地解决杂波环境下的单传感器单目标跟踪问题［9-10］。为了解决杂波环境下的多目标跟踪问题，Bar-shalom等在PDA算法的基础上提出了联合概率数据互联算法（Joint Probabilistic Data Association Algorithm，JPDA），并指出JPDA算法是解决单传感器多目标数据互联的一种良好算法［1-2，4，11-12］。在此基础上，Pao等将单传感器联合概率数据互联算法扩展到集中式多传感器系统，提出了并行、顺序处理结构的集中式多传感器联合概率数据互联算法（Multi-Sensor Joint Probabilistic Data Association Algorithm，MSJPDA），并指出顺序结构MSJPDA算法具有更好的状态估计性能［2，13-14］。

在非线性系统中，MSJPDA算法主要通过将非线性系统线性化，采用基于EKF的集中式MSJPDA算法（MSJPDA/EKF）解决非线性状态估计问题［1，5］。但是，EKF在对非线性系统进行线性化处理过程中须要计算雅克比矩阵，且舍去了高阶项，会引入较大的线性化误差，导致滤波性能下降甚至发散［15］。此外，滤波性能的下降也影响下一时刻目标与量测互联概率的计算，造成各互联事件权重的变化，甚至发生错误关联、滤波发散现象，从而导致整个滤波算法性能下降甚至失效。尽管基于UKF的MSJPDA算法（CMSUJPDA）能够获得比CMSJPDA/EKF更高的估计精度，并且具有更好的滤波稳定性［7］，但是UKF对尺度参数的依赖较大，须要合理调节才能获得理想的滤波效果，并且在高维状态滤波中易出现数值不稳定现象［16-18］。

针对杂波环境下非线性系统中的多目标跟踪问题，基于S-D规则和数据压缩思想，利用CKF滤波算法，提出了一种杂波环境下基于数据压缩的多传感器容积滤波算法（Cubature Klaman Filter Based On S-d Assignment And Data Compressionion，SD-DCCKF）。SD-DCCKF利用广义S-D分配规则对每个传感器送到融合中心的数据进行组合，用极大似然法从所有组合中寻找最佳量测划分，再应用数据压缩的方法将最佳划分中的多个传感器量测数据压缩成一个等效量测数据，并利用容积卡尔曼滤波算法实现状态滤波。

1　多传感器多目标跟踪问题描述

假设在杂波环境中用NS部传感器跟踪NT个目标，对其中任意目标t，1≤t≤NT，假设表示k时刻目标t的状态向量，不考虑输入控制项，则非线性系统离散时间状态方程可表示为

目标t对应于第i个传感器的量测方程为

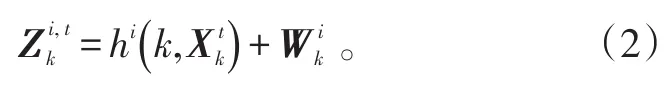
式（2）中：i=1，2，…，NS表示对应的传感器；表示k时刻传感器i关于目标t的量测向量；hi（·）表示传感器i对应的非线性量测函数；表示均值为零、协方差为的高斯量测噪声，且不同时刻的量测噪声序列相互独立，量测噪声序列与过程噪声序列也相互独立。此外，各传感器量测噪声之间也相互独立。

2　SD-DCCKF算法

2.1广义S-D分配

集中式多传感器系统中，各传感器的量测数据被送到融合中心进行统一处理。

一般地，每个量测划分可以看成是NS个传感器对位于ωt处的同一目标的量测集合。由于目标的真实位置ωt是未知的，采用极大化广义似然比求取ωt的极大似然估计：

式（6）中：Hi（·）表示第i个传感器的量测函数；ωi表示第i各传感器位置。

2.2数据压缩

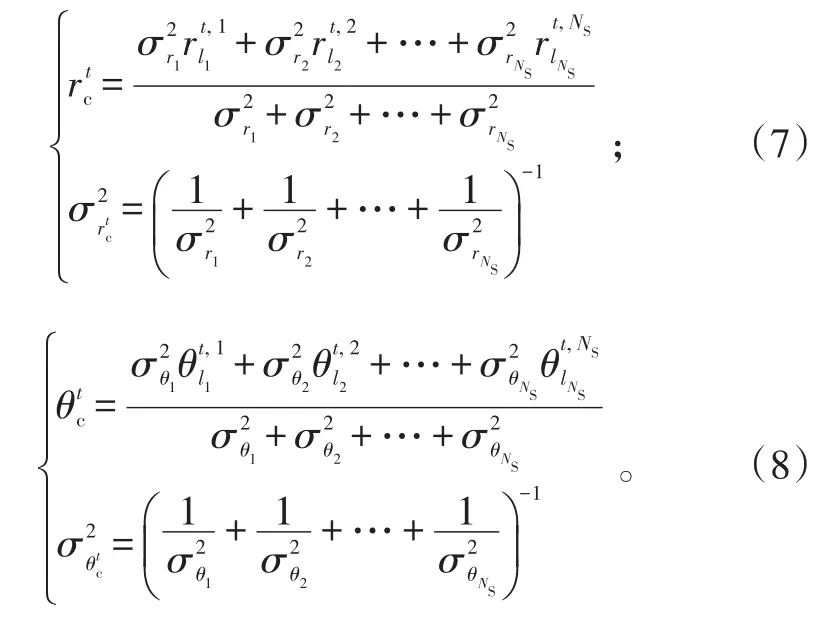
向量形式表示的点迹压缩公式为：

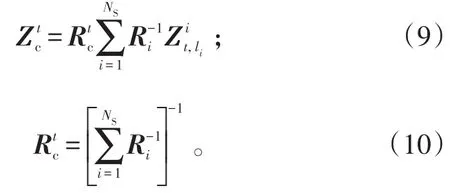
式（9）、（10）中：Ri为第i个传感器的量测噪声协方差；分别表示k时刻目标t的等效量测与等效协方差。

2.3目标状态与协方差估计

经数据压缩后，多传感器多目标跟踪问题便转化为单传感器多目标跟踪问题。对此，可采用CKF对各目标状态与协方差进行递推，并用压缩后的等效量测与等效噪声协方差分别代替目标量测值与量测协方差。CKF通过选取适当的等权容积点传递目标状态均值与协方差，能获得较高的估计精度，且CKF具有UKF的滤波优势，不必调节参数，容积点及其权重的选取只与目标状态的维数有关，可提前计算、存储，且在高维滤波中优势更明显［16-18］。具体的算法实现分为2步进行，即时间更新与量测更新。

Step1：时间更新。

步骤1：前一时刻估计协方差分解

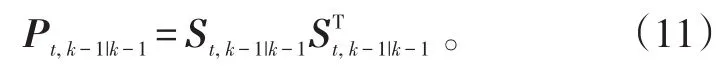
步骤2：计算状态一步预测容积点

式中，［1］j表示集合［1］的第 j列，当=2时，有

步骤3：计算经非线性状态函数传递后的容积点

步骤4：估计目标的预测状态

步骤5：估计目标状态的预测误差协方差

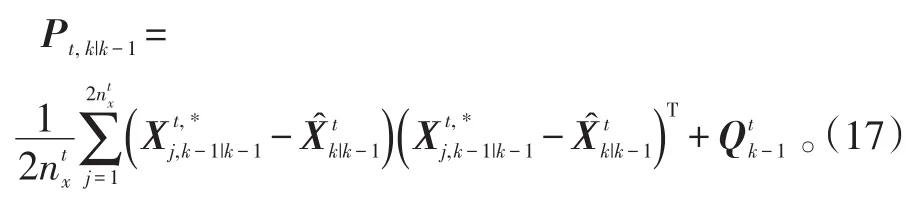
Step2：量测更新。

步骤1：一步预测估计协方差分解

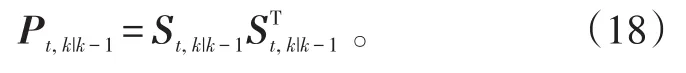
步骤2：计算量测更新容积点

步骤3：计算经非线性量测函数传递后的容积点

步骤4：计算量测的一步预测

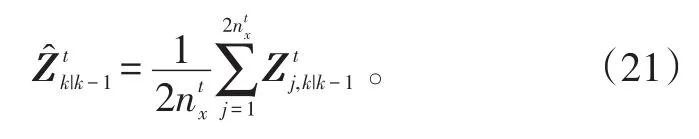
步骤5：计算新息协方差矩阵

步骤6：计算互协方差矩阵

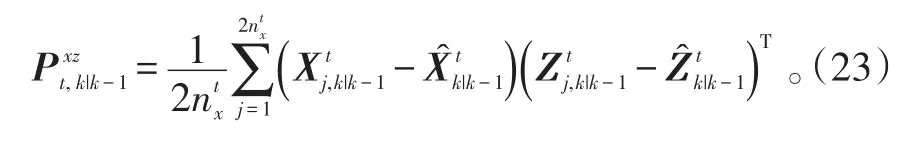
步骤7：计算滤波增益

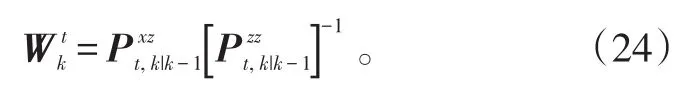
步骤8：计算更新状态与相应的估计误差协方差

3　仿真分析

3.1仿真设置

假设被跟踪目标均在x-y平面内作匀速直线运动，系统的状态方程为

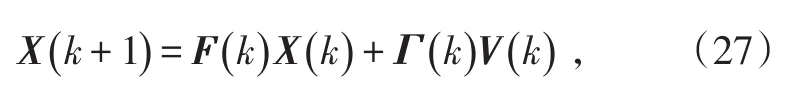
式中，过程噪声分量q1=q2=0.01，

目标的状态为

系统的状态转移矩阵为

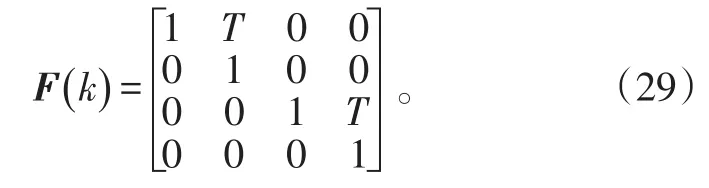
过程噪声分布矩阵为

用3个二维传感器对目标进行观测，传感器i的量测方程为

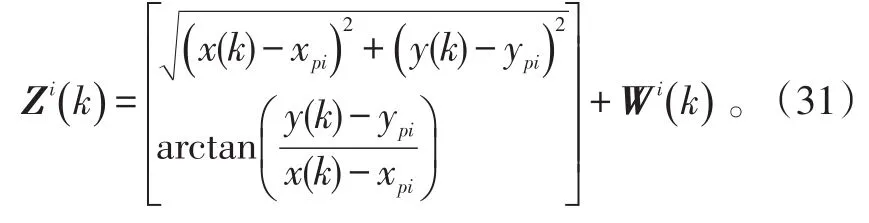
考虑在杂波环境中跟踪2个交叉运动目标，两目标的初始状态分别为：

经过31 s左右，2个目标在（-17 000m，22 000m）处发生交叉。设定蒙特卡洛仿真次数为50次，仿真步长为100步，采样间隔为T=1 s，仿真中采用非参数杂波分布模型，波门内虚假量测的期望数m=2，目标的检测概率PD=0.98，门概率PG=0.999 7，γ=16。由于仿真中初始误差较大，为了更清楚地展示各算法性能的差异，仿真结果中步长都从第10步开始。

3.2仿真结果及分析

图1、2分别为50次蒙特卡洛仿真中3种算法对应的目标1、2在x、y方向的位置均方根误差比较图，图3、4给出了2目标在x、y方向的速度均方根误差比较图。从图中可以看出，3种算法均能对交叉运动目标进行有效地跟踪，其中MSJPDA/EKF算法的估计精度较差，基于数据压缩的2种算法SD-DCUKF和SDDCCKF滤波精度相对较高，且SD-DCCKF精度略高于SD-DCUKF算法，仿真中也更加稳定，收敛速度也相对较快。这主要是由于：①CKF、UKF算法通过选取适当的采样点逼近状态的后验概率密度函数，实现状态滤波，能够获得比EKF算法更高的估计精度，且CKF滤波精度高于UKF算法；此外，状态估计精度的提高减少了近似误差对互联概率的影响，提高了目标与真实量测互联的概率，从而进一步改善了目标状态估计效果；②广义S-D分配给出了最大似然准则下与目标相关联的量测的最优解，减少了虚假量测的影响，目标跟踪性能更佳。

图1　目标1在x、y方向的位置均方根误差比较图Fig.1 Root mean square position error comparison chart atxandydirection of target 1

图2　目标2在x、y方向的位置均方根误差比较图Fig.2 Root mean square position error comparison chart atxandydirection of target 2

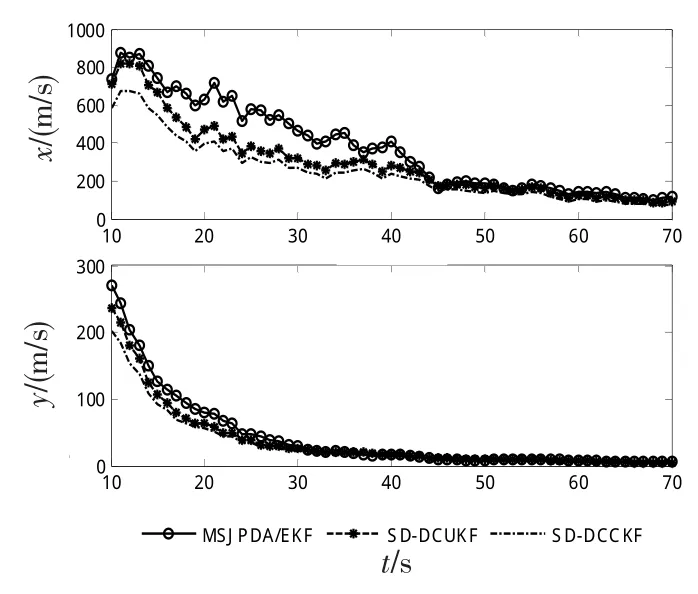
图3　目标1在x、y方向的速度均方根误差比较图Fig.3 Speed mean square velocity error comparison chart atxandydirection of target 1

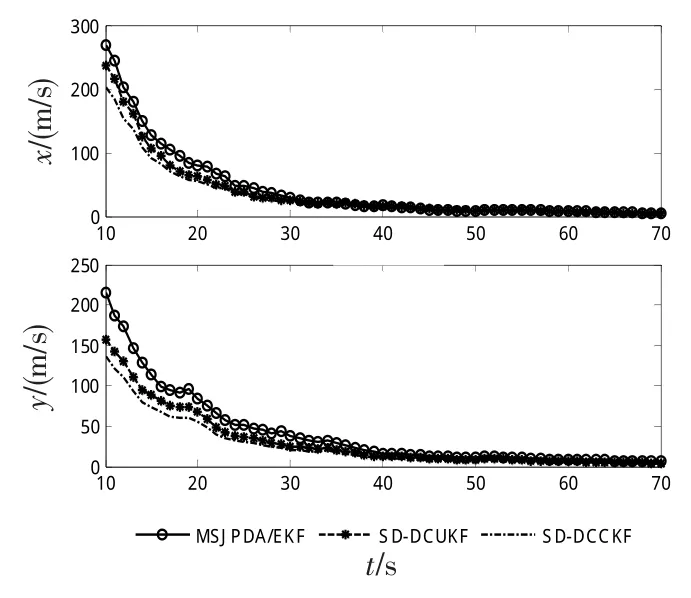
图4　目标2在x、y方向的速度均方根误差比较图Fig.4 Speed mean square velocity error comparison chart atxandydirection of target 2

为了进一步检测SD-DCCKF算法对目标状态的估计效果，图5、6分别给出了3种算法中目标1、2的位置均方根误差比较图和速度均方根误差比较图。从图中可以看出，无论是位置，还是速度，3种算法均能给出有效的估计结果，且基于数据压缩的2种算法SD-DCUKF和SD-DCCKF估计精度较高，且相对于MSJPDA/EKF算法提高了收敛速度。尤其是SDDCCKF算法，具有更佳的目标跟踪性能，在目标跟踪精度和收敛速度方面均优于SD-DCUKF算法。

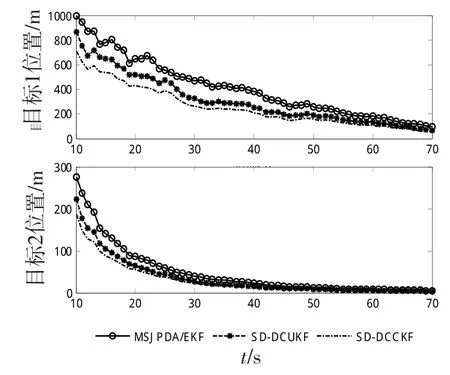
图5　目标1、2的位置均方根误差比较图Fig.5 Root mean square position error comparison chart of target 1 and 2

图6　目标1、2的速度均方根误差比较图Fig.6 Speed mean square velocity error comparison chart of target 1 and 2

此外，MSJPDA/EKF算法是基于扩展卡尔曼滤波理论解决非线性状态估计问题，对模型的线性化处理往往会严重影响状态估计精度，甚至导致滤波发散，且须要计算雅克比矩阵，在高维状态估计中计算量较大，同时滤波精度的降低也会影响互联概率的计算，从而进一步降低目标跟踪精度；SD-DCUKF采用了确定性采样滤波技术UKF进行状态滤波，避免了线性化处理对目标跟踪精度的影响，但是其估计精度受参数影响较大，并且在高维状态滤波中易出现数值不稳定现象；SD-DCCKF基于CKF滤波技术进行状态估计，克服了高维系统中SD-DCUKF数值不稳定的缺点，同时具有较高的估计精度。

综合以上仿真与分析，相对已有杂波环境下非线性系统中多目标跟踪算法，SD-DCCKF在目标跟踪精度、算法收敛速度以及数值稳定性等方面均具有明显的优势。

4　结论

本文主要研究了杂波环境下非线性系统中多传感器多目标跟踪问题。基于广义S-D分配规则，利用多传感器数据压缩原理，结合容积卡尔曼滤波技术，提出了一种杂波环境下基于数据压缩的多传感器容积滤波算法SD-DCCKF。仿真结果及分析表明：SDDCCKF在目标跟踪精度、算法收敛速度以及数值稳定性等方面相对已有算法具有明显优势，为杂波环境下非线性系统中的多目标跟踪问题提供了一种新的可行解决方法。

［1］Y BAR-SHALOM.Multitarget-multisensor tracking：advanced application［M］.University of Connecticut：Artech House，1990：1-6.

［2］何友，王国宏，陆大金，等.多传感器信息融合及应用［M］.2版.北京：电子工业出版社，2010：1-2. HE YOU，WANG GUOHONG，LU DAJIN，et al.Mutisensor information fusion with applications［M］.2nded. Beijing：Publishing House of Electronics Industry，2010：1-2.（in Chinese）

［3］GAO X B，CHEN J G，TAO D C，et al.Multi-sensor centralized fusion without measurement noise covariance by variational bayesian approximation［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47（1）：718-727.

［4］韩崇昭，朱洪艳，段战胜，等.多源信息融合［M］.2版.北京：清华大学出版社，2010：1-3. HAN CHONGZHAO，ZHU HONGYAN，DUAN ZHANSHENG，et al.Multi-source information fusion［M］.2nded.Beijing：Tsinghua University Press，2010：1-3.（in Chinese）

［5］Y BAR-SHALOM.Multitarget multisensor tracking：principles and techniques［M］.Stors C T：YBS Publishing，1995.

［6］耿峰，祝小平.基于模糊多传感器数据融合的目标跟踪系统［J］.火力与指挥控制，2008，33（3）：93-96. GENG FENG，ZHU XIAOPING.Study on target tracking system based on fuzzy multi-sensor data fusion［J］.Fire Control and Command Control，2008，33（3）：93-96.（in Chinese）

［7］管旭军，周旭，芮国胜.集中式多传感器无极联合概率数据互联算法［J］.系统工程与电子技术，2009，31（11）：2602-2606. GUAN XUJUN，ZHOU XU，RUI GUOSEHNG.Centralized multisensor unscented joint probabilistic data association algorithm［J］.Systems Engineering and Electronics，2009，31（11）：2602-2606.（in Chinese）

［8］张晶炜，何友，熊伟.集中式多传感器模糊联合概率数据互联算法［J］.清华大学学报，2007，47（7）：1188-1192. ZHNAG JINGWEI，HE YOU，XIONG WEI.Centralized multisensor fuzzy joint probabilistic data association algorithm［J］.Journal of Tsinghua University，2007，47（7）：1188-1192.（in Chinese）

［9］何友，修建娟，关欣.雷达数据处理及应用［M］.3版.北京：电子工业出版社，2013：1-22，122-129. HE YOU，XIU JIANJUAN，GUAN XIN.Radar data processing with applications［M］.3rded.Beijing：Publishing House of Electronics Industry，2013：1-22，122-129.（inChinese）

［10］修建娟，汪望松，何友.杂波环境下基于距离航速航向信息的多目标跟踪［J］.系统工程与电子技术，2014，36（9）：1702-1706. XIU JIANJUAN，WANG WANGSONG，HE YOU.Multiple target tracking in clutter based on distance speed and course［J］.Systems Engineering and Electronics，2014，36（9）：1702-1706.（in Chinese）

［11］周宏仁，敬忠良，王培德.机动目标跟踪［M］.北京：国防工业出版社，1991：84-88. ZHOUHONGREN，JINGZHONGLIANG，WANG PEIDE.Maneuvering target tracking［M］.Beijing：National Defense Industry Press，1991：84-88.（in Chinese）

［12］HABTEMARIAM B，THARMARASA R，KIRUBARAJAN T，et al.Multiple detection probabilistic data association filter for multistatic target tracking［C］//Proceedings of the 14thInternational Conference on Information Fusion.Chicago，2011：102-106.

［13］O’NEIL S D，PAO L Y.Multisensor fusion algorithm for tracking［C］//American Control Conference.San Francisco，1993：859-863.

［14］PAO L Y，FREI C W.A comparison of parallel and sequential implementation of a multisensor tracking algorithm［C］//American control Conference.Seattle，1995：1683-1687.

［15］JULIER S J，UHLMANN J K.Unscented filtering and nonlinear estimation［J］.Proceedings of IEEE，2004，92（3）：401-422.

［16］ARASARATNAM I，HAYKIN S.Cubature kalman filters［J］.IEEE Transactions on Automatic Control，2009，54（6）：1254-1269.

［17］王晓旭，潘泉，等.非线性系统确定性采样型滤波算法综述［J］.控制与决策，2012，27（6）：801-812. WANG XIAOXU，PAN QUAN，et al.Overview of deterministic sampling filtering algorithms for nonlinear system［J］.Control and Decision，2012，27（6）：801-812.（in Chinese）

［18］孙枫，唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波故你精度的比较［J］.控制与决策，2013，28（2）：303-308. SUN FENG，TANG LIJUN.Estimation precision comparison of cubature kalman filter and Unscented kalman filter［J］.Control and Decision，2013，28（2）：303-308.（in Chinese）

Algorithm of Muti-Sensor Cubature Filter Based on Data Compressionion Under Clutter Environment

LIU Juna，LIU Yub，DONG Kaia，SUN Shunb
（Naval Aeronautical and Astronautical University a.Graduate Students’Brigade；b.Institute of Information Fusion，Yantai Shandong 264001，China）

According to the multi-sensor multi-target tracking problem of nonlinear systems in a cluttered environment，a novel cubature Klaman filter algorithm based on M-D assignment and data compressionion（MD-DCCKF）was proposed. In the new algorithm，the measurements from each sensor were permuted and combined，and the best combination would be found according to a rule.Then，the best combination would be compacted into an equivalent measurement which was associated with targets by using the MSJPDA techniques.Finally，the targets’state would be estimated based on cubature Kalman filter.Simulation results showed that MD-DCCKF outperformed the existing algorithms in the aspects of tracking accuracy，convergence rate and filtering robustness.

M-D assignment；data compression；multi-sensor；multi-target tracking；data association；cubature Kalman filter

TP953；TN957

A

1673-1522（2015）06-0531-06DOI：10.7682/j.issn.1673-1522.2015.06.007

2015-07-24；

2015-09-18

国家自然科学基金资助项目（61471383）

刘俊（1990-），男，硕士生。